稳健声线扰动特征用于浅海小目标定位∗

刘帅京 许 枫 杨 娟

(1 中国科学院声学研究所 海洋声学技术中心 北京 100190)(2 中国科学院大学 北京 100049)

0 引言

港口浅海区域的水下监视系统对港口的安全防护具有重要的意义。北约水下研究中心(NATO Undersea Research Centre,NURC)提出了将垂直发射阵和垂直接收阵组成的声学绊网用于水下入侵目标的探测[1]。前向散射信号的强度比其他方向的信号强度更强更稳健，应用前向散射信号进行目标探测具有探测距离远、受其他方向影响小等优点，然而前向散射信号受到强直达波的干扰造成前向散射信号的检测十分困难[2−3]。在近距离的小目标探测问题中，信道起伏变化引起的声场扰动可能会淹没前向散射信号引起的扰动，因此需要研究稳健的目标探测和定位算法，以适用于动态的海洋环境。

当目标位于发射和接收的连接线附近时，目标的前向散射信号与直达波信号产生“遮蔽效应”，造成接收信号的能量减小，引起一些特定路径的声线发生扰动，应用这一特性，可采用扰动声线类的方法实现浅海的目标定位。Folegot等[1]提出将目标引起的扰动声线进行几何交汇实现目标定位，并通过处理BARRIER-04的实验数据验证了算法的有效性。Marandet等[4]开展了应用超声波的等比缩放实验模拟了浅海环境，并利用扰动声场的波动理论将目标定位问题转化为声场波阻抗的反演问题。Yildiz等[5]应用多基地系统，采用基于数据的扰动声压敏感核方法实现了目标定位。

唐浩等开展了湖上实验，应用20～28 kHz的线性调频信号将扰动声线类算法用于自然环境中的小目标定位，用小尺寸的充水铁球代替目标，利用声压敏感核的空间分布与声线传播路径保持一致的特性实现了基于扰动声压敏感核的目标定位，并对阵列、海底起伏等因素进行了分析[6−7]。

以上的研究和实验都是在较为平稳的环境下进行的，平稳环境中可以假设目标引起的声场扰动远大于信道自身变化引起的声场扰动，然而在海洋环境中，高频条件下的信道起伏对声场的影响较大，接收信号的到达结构因信道变化存在不稳定性，从而会影响扰动声线类目标定位算法的性能。为此，本文开展了港口浅海环境的蛙人穿越实验，实验中采用了中心频率为22.5 kHz、带宽为15 kHz的线性调频信号。从实验中的声场扰动情况可知，虽然动态海洋环境中的接收信号存在不同程度的起伏，但是仍然有一部分传播声线对应的接收信号受信道变化的影响较小，因此提出了基于稳健声线扰动特征的目标定位方法，该方法利用蛙人穿越发射阵和接收阵组成的垂直平面时引起的稳健声线扰动特征，从而实现动态信道变化条件下的小目标定位。

1 基于稳健声线扰动的目标定位方法

1.1 目标引起声场扰动的波动理论

令G(ω;rr,rs)表示声源rs到接收点rr之间的格林函数，ω为信号的角频率，在各向同性的介质中，格林函数满足亥姆霍兹方程，即

当介质中的传播速度c和密度ρ发生局部扰动变为c+δc和ρ+δρ时，扰动后的格林函数G+δG满足

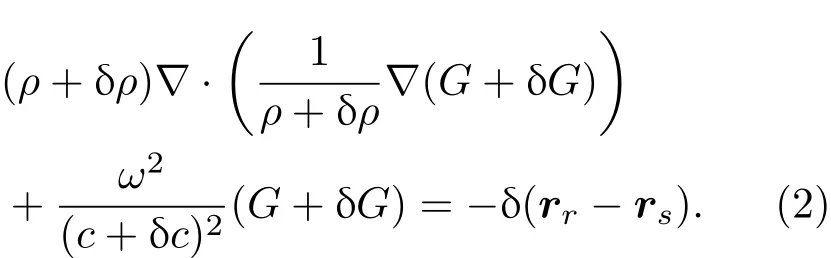
根据文献[4]中的推导，在一阶Born近似的条件下，位于r′处的小目标引起的扰动格林函数为

其中，φs表示向量rr−rs和向量r′−rs之间的夹角，φr表示向量rs−rr和向量r′−rr之间的夹角，散射角φs和φr的示意图如图1所示。

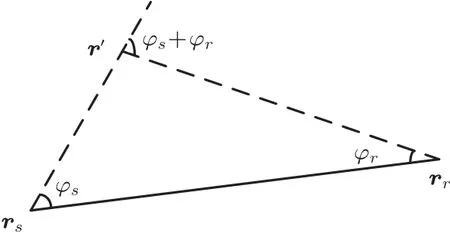
图1 目标散射角度的示意图Fig.1 The illustration of the scatter angles

从式(3)可以看出，目标引起声场扰动的本质是目标所在位置的声速和密度发生了变化。

1.2 水声信道中的扰动声压变化

在远场条件下，目标的散射特性可以用形态函数f∞来表示，设入射场为p0，那么散射信号ps(r)可以表示为

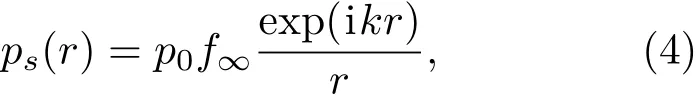
其中，k是波数，r表示接收点到散射体的距离。对于小的球体目标，即当ka≪1时(a是球体目标的半径)，形态函数f∞具有如下的形式：

在一阶Born近似的假设条件下，式(6)可以表示为

其中，j1(x)表示一阶球形贝塞尔函数。

设声场中发射信号的频谱为S(ω)，应用逆傅里叶变换可以得到接收声压场p0(t;rr,rs)和扰动声压场δp(t;rr,rs,r′)的表达式分别为

那么接收声场的相对声压变化表示为[8]

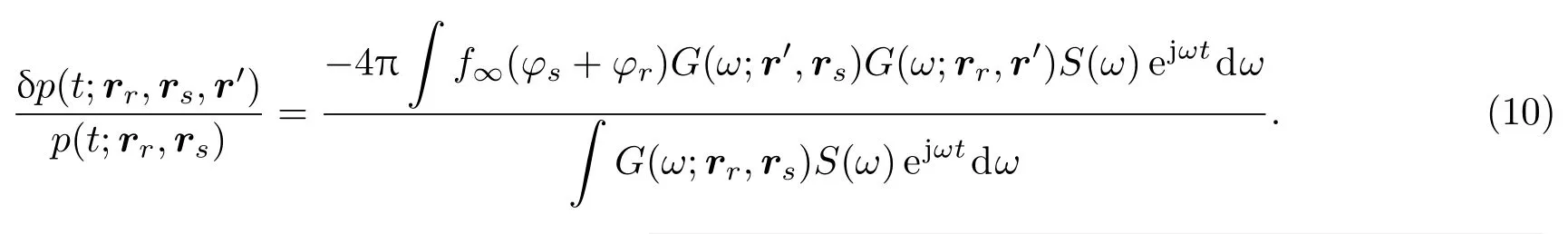
对于浅海中的多途信道，不同路径的传播信号可以看作是声源关于反射界面的虚源对应的接收信号，经界面反射后的声线对应的相对声压变化分布可以通过虚源与接收点之间的对应声线关于界面折叠得到[4]。应用式(10)的表达式，在水深为10 m、收发距离为50 m的声场中对相对声压变化的分布进行仿真，设声速沿深度均匀分布，声速值为1500 m/s，声源位于水下5 m，接收水听器位于水下5.5 m，设发射信号是中心频率为22.5 kHz、带宽为15 kHz、时间宽度为10 ms的线性调频信号。图2给出了一次水底反射路径的相对声压变化分布图，水平距离和垂直距离上的步长分别设为0.05 m和0.025 m，小目标球的参数设为半径为0.2 m的铁质实心球，图中每个点的值表示的是目标位于该点时一次水底反射波的相对幅值变化，该图的数值分布表明了扰动声压敏感核的空间分布形状与声线路径保持一致，当目标位于传播声线附近的第一菲涅耳区内时，接收信号的相对声压变化为负值。

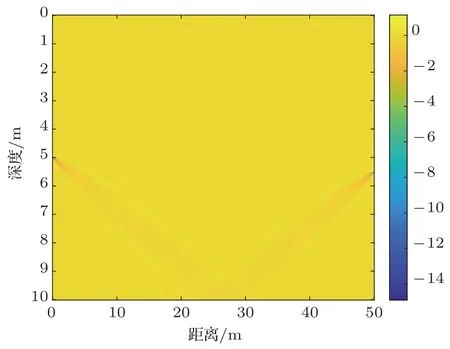
图2 一次水底反射路径的扰动声压敏感核空间分布Fig.2 The spatial distribution of pressure kernel for eigenray of the once bottom bounce

1.3 基于稳健声线扰动特征定位方法的处理流程

本文采用的探测系统由发射垂直阵和接收垂直阵构成，如图3所示，图中的SA和RA分别表示发射阵列和接收阵列，T表示目标，多组发射和接收之间的本征声线构成了用于目标探测的声学绊网。当目标位于某一条传播声线上时，目标引起的遮蔽效应会造成该声线的到达波信号出现“阴影”，对应了声压敏感核在第一菲涅耳区内的负值，对于没有照射到目标上的声线，接收信号的扰动非常微弱，可忽略不计，因此可以通过对发生明显扰动的声线(或未发生扰动的声线)进行几何交汇实现目标定位。

图3 探测系统示意图Fig.3 The illustration of the detection system

实际的海洋环境中，高频条件下的接收信号扰动受信道自身起伏的影响较大，但在一定的条件下，某些路径的扰动受信道的影响较小，将这些受信道影响较小的声线称为稳健声线，本文提出的基于稳健声线扰动特征的定位方法就是通过筛选这些稳健声线中的扰动声线进行目标定位的，图4给出了该定位方法的处理流程图，实现过程如下：

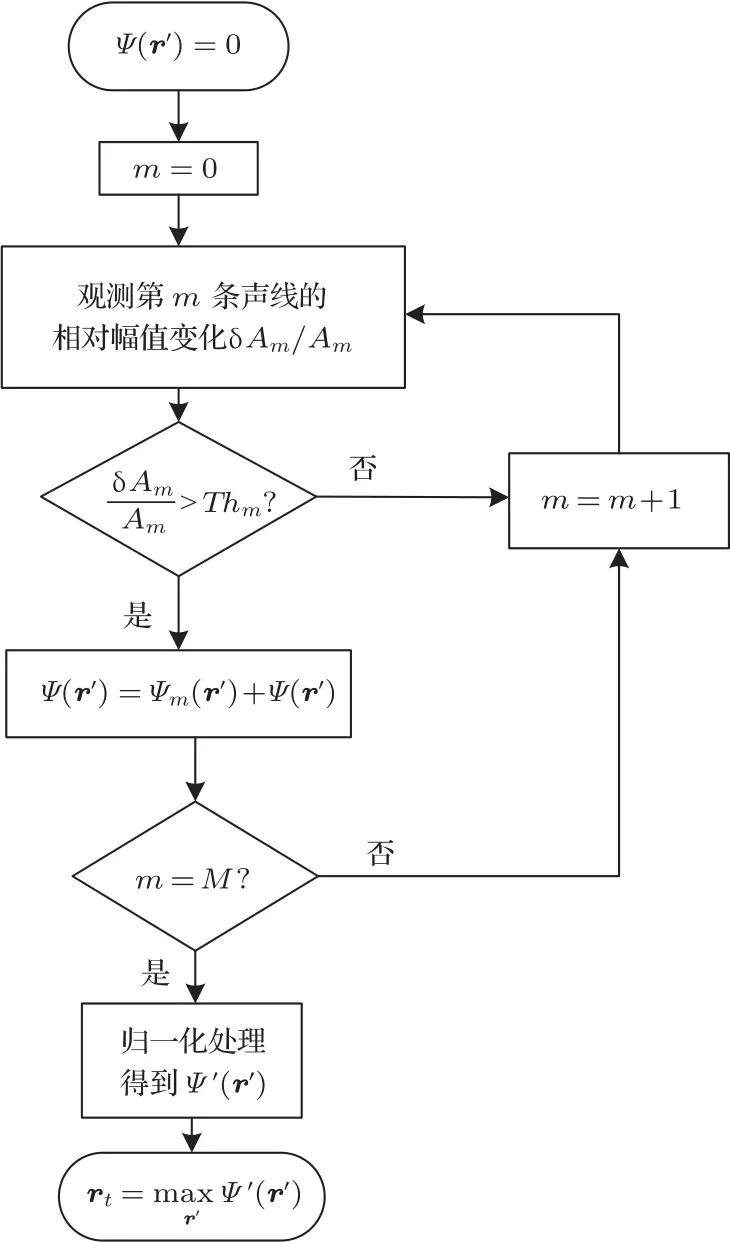
图4 扰动声线定位方法的处理流程图Fig.4 The scheme of the localization method based on perturbed eigenrays

(1)稳健声线提取：观测无目标时的背景声场，根据不同传播路径到达波的传播时延和信号幅值的扰动情况提取接收信号到达结构中的稳定成分，稳定到达结构中的所有到达声线作为稳健声线，构成待筛选声线的集合Q，设集合中声线元素的个数为M；

(2)确定筛选阈值：以无目标条件下的背景声场中到达信号幅度的平均值作为参考幅度，设集合Q中第m条声线的参考幅度为Am，幅度扰动量为δAm，那么该声线的相对幅值变化为δAm/Am，通过观测相对幅值变化的分布和扰动情况确定阈值Thm；

(3)筛选扰动声线：依次观测集合Q中声线的相对幅值变化，如果相对幅度变化大于设定的阈值Thm，则将第m条声线加入扰动声线集合Q中；

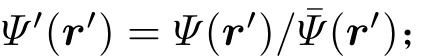
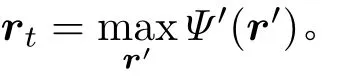
2 湖试实验和性能分析

直接对浅海声场中的目标前向散射信号进行建模较为困难，本节先对文献[6]中的湖试实验数据进行处理，分析稳健声线集大小对探测区域和定位结果的影响。

2.1 湖试实验介绍

湖试实验的实验系统和图3基本相同，图5给出了发射阵和接收阵的布局图，发射阵由5个发射换能器组成，接收阵由16个接收阵元组成，发射阵和接收阵均为刚性连接。发射阵元的深度分别为9.9 m、10.3 m、10.7 m、14.1 m和18.1 m，接收阵元则均匀分布在水下4.2～16.2 m，水深约为24 m，收发距离约为71 m，水底地形未知。图6是声传播速度随深度的分布情况，水深小于5 m时，声速近似均匀分布，声速值约为1452 m/s，在水深大于5 m时，声速呈负梯度下降。

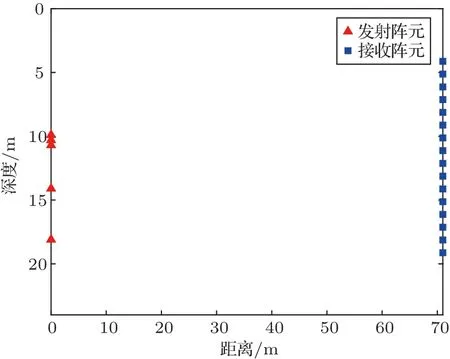
图5 湖试实验阵元布放示意图Fig.5 The illustration of the positions of sources and receivers in lake experiment

图6 湖试实验环境的声速分布曲线Fig.6 The curve of sound speed pro file in lake experiment

实验中采用半径为0.2 m的充水铁球作为目标球，通过绳子连接目标球和水面浮子，目标球和浮子之间的绳长即目标位于水下的深度，应用GPS对水面浮子进行定位，从而间接确定目标的位置。保持水面浮子位置不变，那么在平稳环境的条件下，可以假设目标的位置保持不变。各个发射阵元单独反射信号，发射信号的周期为0.5 s，然后分别记录不同发射阵元对应的接收信号矩阵。实验中采用的发射信号为中心频率为24 kHz、带宽为8 kHz、时间长度为10 ms的线性调频信号，接收信号的采样频率为120 kHz。在图3所示的探测系统中，以发射垂直阵所在直线与水面的交点为原点建立直角坐标系，设水平指向接收阵的方向为x轴方向，垂直指向海底的方向为z轴方向。

两个垂直阵的阵元分别从上至下进行编号。图7给出了第1号发射阵元对应的阵列接收信号经匹配滤波后的输出结果，图中的数据是采用时间长度为35 ms的时间窗截取出的信号部分，横坐标的时间表示相对到达时间，从图7中可以看出不同深度的接收信号具有不同的信号到达结构，且根据这些到达结构可清晰地分辨出不同传播路径的到达波信号。

图7 第1号发射阵元对应的接收阵列信号结构Fig.7 The received structure of the 1stsource element

以第4号接收阵元的接收信号为例分析接收信号的到达结构，如图8所示，从图中可以看出，接收信号中主要存在5条主要的到达波，分别对应直达路径、一次水底反射路径、一次水面反射路径、水面-水底反射路径和水底-水面反射路径，这些路径的到达信号已用数字#1～#5标出，同时可以从图中观察到，除这5条主要途径之外还存在一些散射信号干扰了真实的到达信号，如图8中用“*”标出的到达波，这与未知的海底环境以及水下可能存在的其他反射源有关。

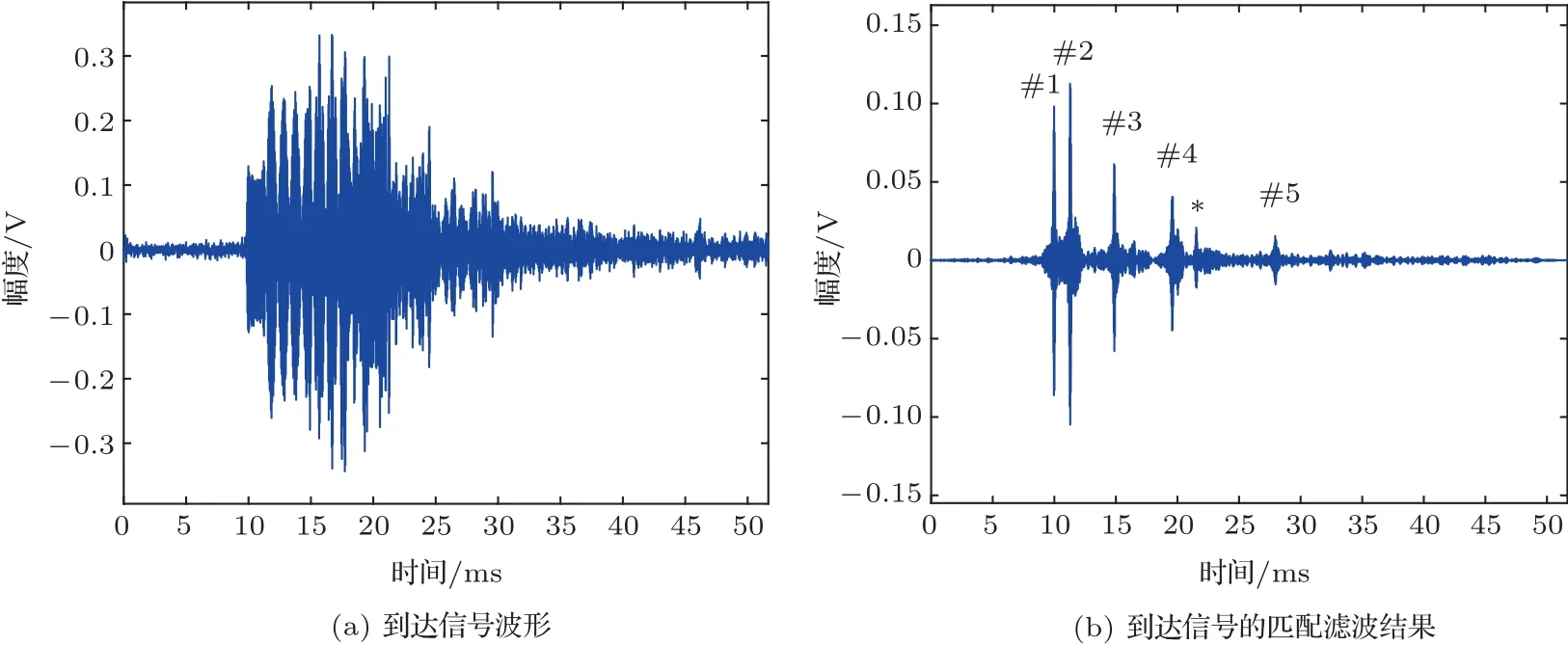
图8 第1号发射阵元、第4个接收通道的接收信号结构Fig.8 The received structure of the 1stsource element and the 4threceiving channel

考虑每对收发之间的5条主要到达成分，得到如图9(a)所示的本征声线分布图。提出的目标定位方法主要是通过筛选稳定到达结构中的扰动声线实现的，因此该探测系统的探测范围即待筛选声线集Q中所有声线的第一菲涅耳区形成的区域，结合扰动声压敏感核的空间分布，可以得到该实验中的探测范围如图9(b)所示，从图中可以看到，由于阵元位置分布以及不同传播声线路径的差异，探测区域内不同位置的声线分布密度不相同，在湖试实验的阵列参数条件下，探测区域的左上方、左下方、右上方和右下方4个区域均为探测盲区。

图9 湖试实验的探测区域Fig.9 The detection area in lake experiment

2.2 定位结果

高频条件下，小目标的前向散射信号引起的接收声场扰动非常微弱，海洋中信道自身的变化引起的声场扰动有可能会淹没穿越目标对接收声场引起的扰动，从而影响定位结果。然而在一定的条件下，声场中一些特定的传播声线受海面等环境因素的影响较小，信号到达结构可以保持相对稳定。仅采用接收声场到达结构中稳态成分中包含的稳健声线进行定位，不仅可以简化计算量，而且可以提高动态环境中定位算法的鲁棒性。本节对湖试实验中目标位于(8.0 m,14.1 m)的接收数据进行分析，分别对声线数目较多的声线集定位结果和对声线数目较小的声线集定位结果进行分析，验证本文提出的定位方法的可行性。

首先分析各个发射阵元对应的阵列接收信号结构，根据不同传播路径的本征声线到达时间的差异分离声线，然后将所有可区分的声线记录到集合Q中。由于该实验环境中的接收信号主要有5个到达成分，因此每对发射-接收之间只记录5条到达声线。

对比无目标条件下和有目标条件下的接收信号，每个声线的幅值采用连续11个发射周期内的平均值进行计算，并统计集合Q中每条声线的相对声压变化，然后分析发射-接收之间所有声线的相对声压变化分布，得到图10所示的结果，图10(a)和图10(b)分别表示无目标和有目标时的相对声压变化统计结果，从图中可以看出，当声场中没有目标时，各个声线的相对声压变化分布曲线的峰值位于0，且正扰动和负扰动的数量基本保持平衡；而当目标出现在声场中时，发生负扰动的声线数目增多，正扰动和负扰动的数量出现明显的差异，另外可以观察到，有目标存在时，声线相对声压变化的范围明显大于无目标情况下的扰动范围。

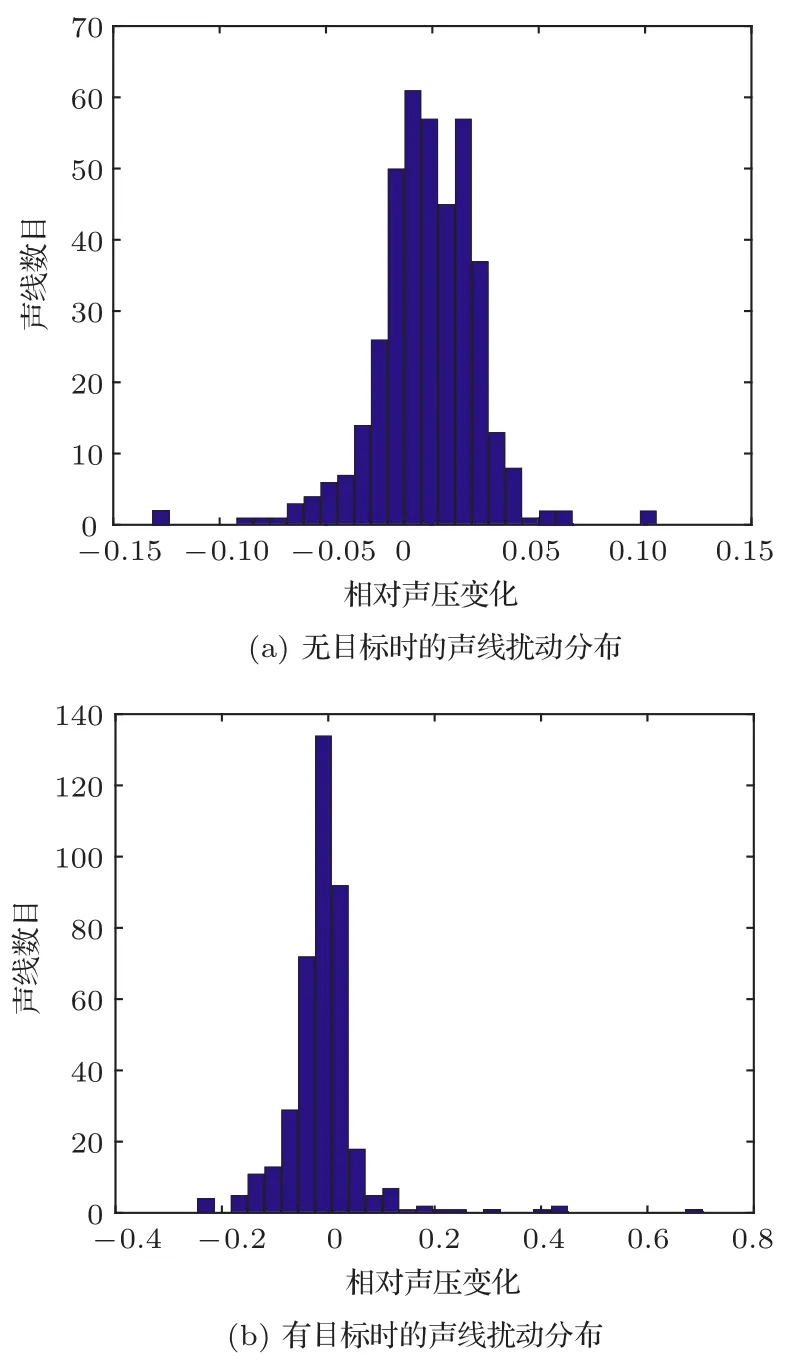
图10 相对声压变化统计结果Fig.10 The distributions of relative pressure changes

在发射阵和接收阵构成的探测平面内，x轴和z轴均采用0.1 m的间隔对探测区域进行划分，然后根据图10(b)中各个声线相对声压变化的分布情况确定扰动声线的集合Qp，并应用式(10)分别计算每个扰动声线的相对声压变化值，最后采用1.3节中处理过程的第(4)步和第(5)步得到目标球的定位模糊图，如图11(a)所示。从图11(a)中读取亮点区域的位置作为目标位置的估计值，即(7.2 m,14.4 m)，与理论值相比，定位结果的绝对误差为(0.8 m，0.3 m)。图11(b)和图11(c)分别给出了x=7.2和z=14.4时定位模糊图的截面曲线，分别对应目标所在位置的垂直线和水平线，对比两幅图可以看出，在该湖试实验的条件下，扰动声线类目标定位方法得到的目标位置在深度方向上的精度更高，主瓣宽度大致为6.6 m，而在水平方向上的主瓣宽度大致为14.2 m。

图12(a)给出了仅采用直达路径声线的定位结果，图12(b)给出了仅采用直达路径和一次水底反射路径的定位结果，结合图11进行对比，结果表明采用掠射角更大的声线可以增加目标位置的相关信息，从而提高目标定位的精度。对于实验中的目标位置，直达路径的扰动声线提供了目标的深度信息，而一次水底反射路径的声线扰动提供了目标的距离信息，因此仅采用直达路径和一次水底反射路径即可确定目标位置的大致范围，但与图11相比，定位结果的精度具有一定的损失。

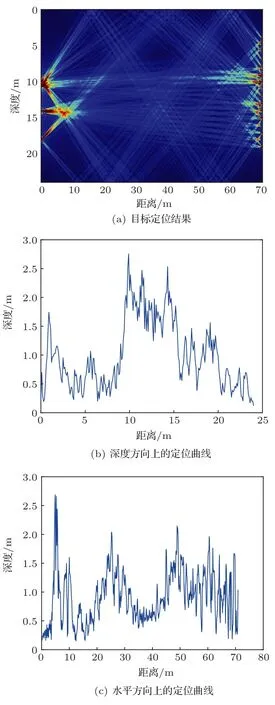
图11 湖试实验的定位结果Fig.11 Location result of the lake experiment

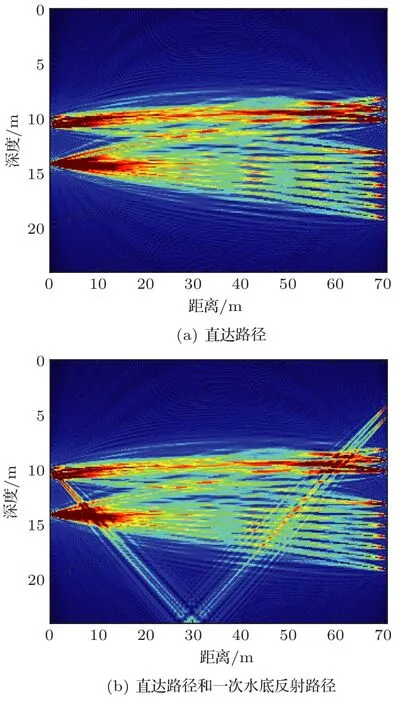
图12 不同声线集合下的定位结果Fig.12 Location result with different set of eigenrays

3 海上实验

3.1 海上实验介绍

在深度为5.5 m、收发距离为50 m的海洋环境中开展蛙人穿越实验，发射阵和接收阵均为8个阵元组成的垂直阵，阵元间距均为0.6 m，从上至下给垂直阵的阵元编号，发射阵的第1号阵元位于水下1.1 m，接收阵的第1号阵元位于水下1.2 m，发射阵和接收阵均为刚性连接，且两个垂直阵通过GPS系统进行时间同步，图13给出了海试中各个阵元布放位置的示意图。采用温盐深仪(Conductivity,temperature,depth,CTD)测量得到的声速分布曲线如图14所示，从中可以看出，声传播速度在声场中均匀分布，声速值约为1535 m/s。

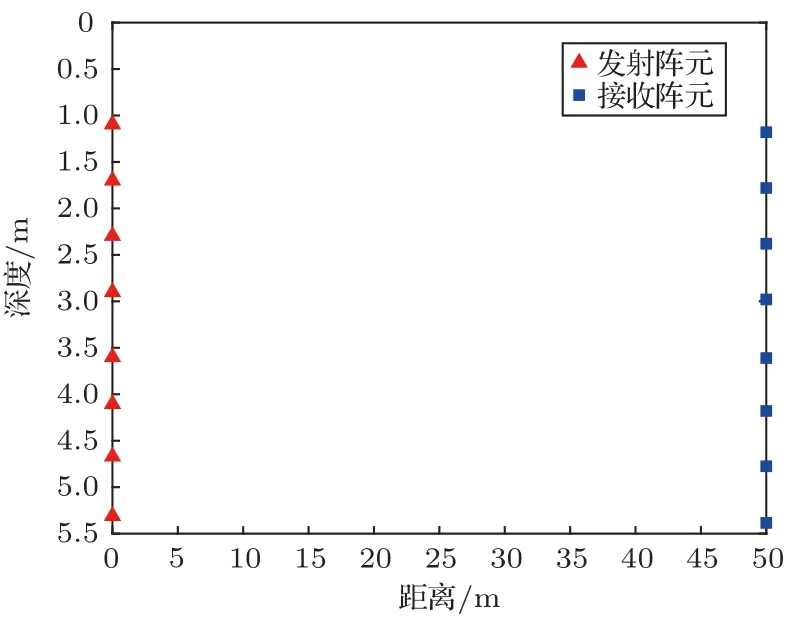
图13 海试实验阵元布放示意图Fig.13 The illustration of the positions of sources and receivers in sea experiment

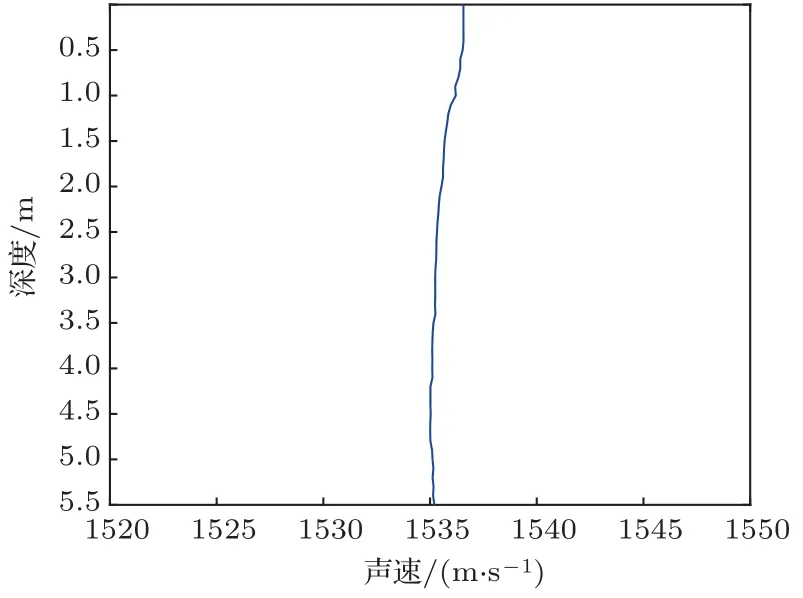
图14 海试实验环境的声速分布曲线Fig.14 The curve of sound speed pro file in sea experiment

实验中的发射信号为中心频率为22.5 kHz、带宽为15 kHz的线性调频信号，时间宽度为10 ms，采样率为120 kHz，由潜水员横穿收发连线模拟蛙人穿越基线的情况，在目标穿越过程中，发射阵列的发射源依次发射信号，发射信号周期为0.5 s。图15是实验中采用的两条目标穿越轨迹的示意图，两次穿越的位置分别与收发中点的距离为10 m和0.5 m，实验中目标穿越时的深度不能确定。

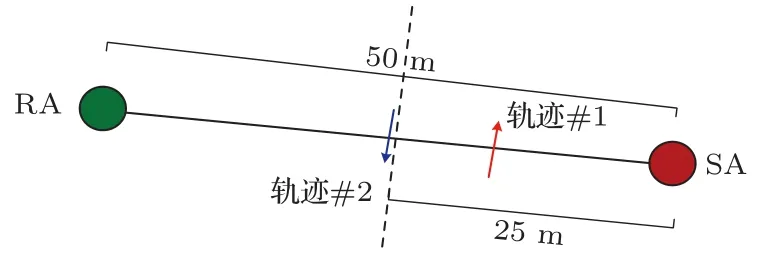
图15 目标穿越时的运动轨迹示意图Fig.15 The diagram of tracks of the crossing target

以第2号发射为例，图16给出了第5号接收阵元的接收信号在400 s内的接收到达结构变化，从图中可以看出该接收信号主要有5个到达成分，在图中已分别用数字#1～#5标出，前3个到达波分别对应直达路径、一次水面反射路径、一次水底反射路径，每个到达波随着时间发生不同程度的扰动。从图16中可看出，第1条和第3条到达波的扰动幅度最小，第2个到达波的传播时延和幅度的变化范围较大，这主要是因为第2条到达波经过了一次海面反射，海面受波浪和风速等影响产生的水面起伏引起了第2条到达波的扰动。

图16 第2号发射阵元、第5号接收通道在400 s内的到达结构变化Fig.16 The dynamic received structure of the 5th receiving channel with the 2ndsource in 400 s

图17是第2号发射阵元对应的阵列接收信号结构，由于海试环境中水深和收发距离的比值较小，第1条到达波和第2条到达波的传播时延相差较小，与图7中湖试数据的接收结构相比可以观察到，海试实验的接收信号结构更为复杂。

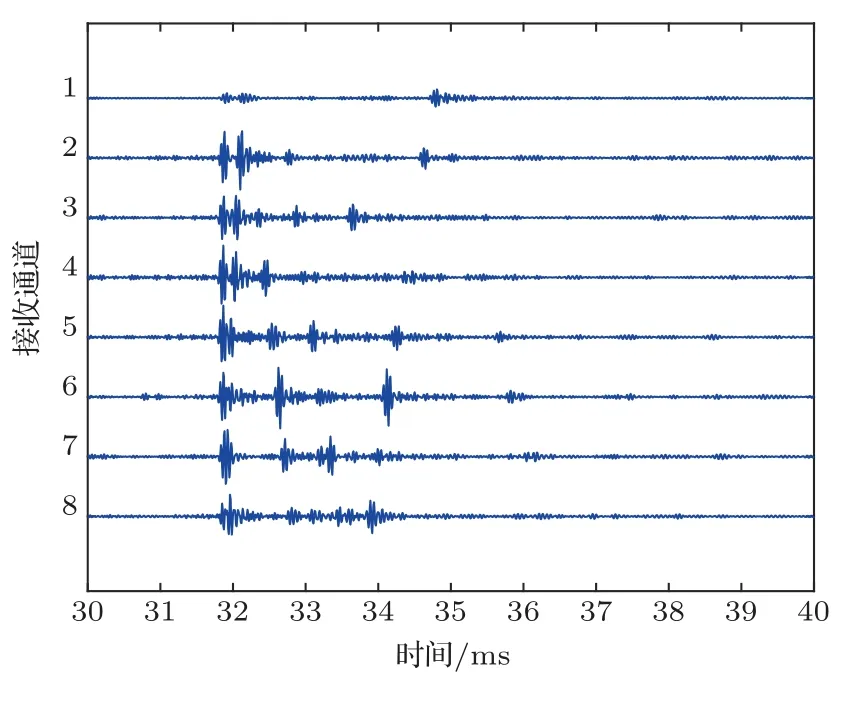
图17 第2号发射阵元对应的接收阵列信号结构Fig.17 The received structure of the 2ndsource element

3.2 探测区域分析

根据海试实验的环境和阵元位置，得到声场中的声线分布图和探测区域如图18所示，此处的每对发射和接收之间仍选用5条声线进行分析。由于海试环境中的阵元位置在水下的分布比较分散，海试探测盲区较小，值得注意的是，这里的海底假设为平面，而实际上的海底地形会更复杂。对比图9(b)和图18可以看出，在海试条件下均匀分布的阵元构成的探测区域中，声线分布的密度更均匀。

图18 海试实验的探测区域Fig.18 The detection area in sea experiment

对每对发射-接收对应的接收信号到达结构的动态变化图进行分析，根据每条声线的幅值和到达时延等参数的扰动情况人工选取稳健声线。图16的动态分析结果表明，在海洋环境中，经海面反射的声线受到的影响较大，因此稳定的到达结构中主要包含直达路径和一次水底反射路径，那么稳健声线集合Q中一共包含128(8×8×2)条声线，根据这些稳健声线的分布可以得到基于稳健声线扰动特征定位方法的探测区域，如图19所示。

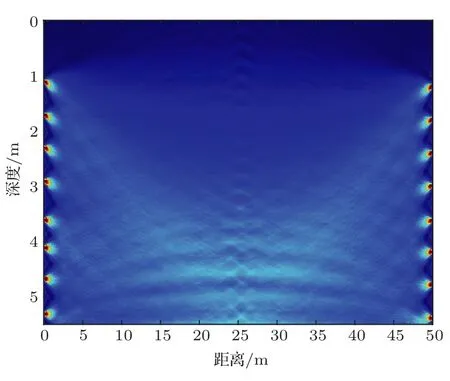
图19 稳健声线的探测区域Fig.19 The detection area with robust eigenrays

对比图18和图19的结果可以看出，由于舍弃了受环境影响较大的大掠射角声线，稳健声线构成的探测区域变小，且声线分布密度在探测的区域内的分布变得不均匀，此时的探测范围主要依赖两个垂直阵的阵元分布与海底构成的区域，靠近海面的部分变为探测盲区，因此可以通过改变第1号阵元与海面的距离调整探测区域。

3.3 筛选扰动声线

以图15中的目标运动轨迹#1为例介绍筛选扰动声线的过程。图20(a)是第8号发射的第8号接收通道的直达路径信号在目标穿越过程中的扰动情况，图20(b)是第7接收通道和第7接收通道的直达路径信号在目标穿越过程中的扰动情况，这两幅图分别表示了没有受到目标影响的声线扰动情况和目标引起扰动的声线变化，图中的红色横线表示无目标时接收信号幅度的平均值。

图20 不同声线的扰动情况Fig.20 The perturbation of different eigenrays

在目标的穿越过程中，分别观测集合Q中每一条稳健声线的相对声压变化情况，并根据每条声线的实际情况设定阈值，筛选扰动声线，从而确定扰动声线的集合Qp。有些声线的扰动曲线可能会出现非目标引起的扰动尖峰，如图20(b)中用黑框标出的部分，这一方面可能来自于动态海洋环境自身引起的接收信号变化，另一方面可能来自于传播时延估计值与实际接收信号结构的误差，因此这里只对同一时刻发生扰动的声线进行筛选，以排除环境等影响因素，多条声线同时发生扰动的时刻则代表了目标穿越收发连线的时刻。

3.4 定位结果

处理图15中的目标运动轨迹#1和运动轨迹#2，对筛选出的扰动声线进行几何叠加，水平方向和垂直方向的划分间隔分别设为0.05 m和0.025 m。图21给出了两个穿越轨迹的定位模糊图，得到的定位结果分别为(3.975 m,13.3 m)和(3.4 m,25.25 m)。根据图15给出的目标运动轨迹示意图，目标两次穿越基线时与发射阵列的距离(即x轴坐标)为15 m和25.5 m，和图21给出的定位结果相比相差不大，可认为本文提出的方法可在浅海港口环境中对穿越目标进行定位。

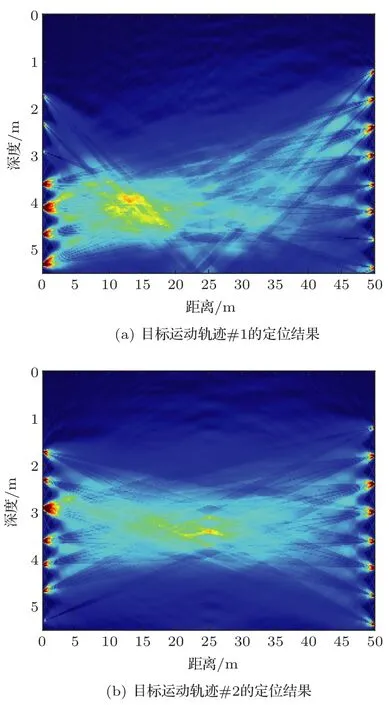
图21 海试实验的定位结果Fig.21 Location result of the sea experiment

综上，本文提出的方法主要依赖于接收信号中稳定成分的扰动情况，当自然环境非常恶劣，以至于无法提取出稳健声线时，该方法将会失效。综合湖试和海试的实验结果可知，扰动声线类目标定位方法的探测范围主要与阵元分布以及观测声线的分布有关，阵元在水下覆盖的深度越深，阵元分布的分散程度越大，探测范围则越大。小掠射角的声线可以提供目标可能存在的大致范围，结合大掠射角声线则可以确定目标位置，提高定位精度。

4 结论

为研究动态海洋环境中的扰动声线类定位方法，本文提出了基于稳健声线扰动特征的目标定位方法，应用湖试实验的目标球数据验证了所提算法的可行性，然后通过对海试数据进行处理，分析了接收信号中的主要到达成分，得到了声场的稳定到达结构，从而将该算法应用于港口的海洋环境，实现了穿越蛙人在探测平面内的目标定位。

本文中的实验是在动态海洋环境下进行，且实验中的收发距离与水深的比例约为1:10，与超声等比缩放实验和湖试实验相比更具有说服力和实用价值，实验的结果说明了仅采用直达路径和一次水底反射路径等受海面影响较小的声线即可实现目标定位，该方法不仅可以减小算法的复杂度，而且在动态环境中具备一定的鲁棒性。