浅海低频长线阵声源方位估计∗
梁玉权 周士弘 宫在晓
(1 中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)
(2 中国科学院大学 北京 100049)
0 引言
根据浅海波导低频声传播的简正波理论和平面波假设,水平阵接收点源激发的声场是由不同的模态叠加而成,每阶模态对应一个来波方向,每个来波方向是由声源实际方位角和声源激发模态的俯仰角耦合而成。如果采用常规波束形成(Conventional beamforming,CBF)的声源方位估计方法,将会产生估计方位相对真实方位的偏移和分裂现象,特别是声源靠近长线阵端射方向时,这种现象更加明显。解决该问题的基本思路是将声传播模型引入到方位估计中[1],为此,很多学者提出了基于水平阵和浅海简正模态理论的声源方位估计方法。
1998年,Yang[2]将水平直线阵的阵元域-场匹配处理,扩展为波束域-波束匹配处理,实现与匹配场处理类似的浅海声源方位的无偏估计。然而,采用全模态场的阵元域或波束域匹配处理,并不能改善固有的环境失配的影响,且进行深度、距离和方位角三维参数空间搜索运算量较大。2004年,Lakshmipathi等[3]提出了子空间相交(Subspace intersection,SI)方法,将浅海目标声源方位估计与简正波模型结合起来,利用信号子空间与模态子空间的相交特征,对方位角进行一维的空间优化搜索,缩减了计算量。2006年,张爱民等[4]提出约束最小二乘子空间相交方法和总体最小二乘子空间相交方法,改善SI方法在进行矩阵奇异值分解时的数值稳定性。2013年,易峰等[5]基于正交投影子空间分解原理进行浅海声源方位估计。由于SI方法估计信号子空间准确性依赖于样本协方差矩阵奇异值分解,因此并不适用于快拍数较少的低信噪比接收信号,在存在相干源和未知声源个数的情况下,子空间估计精度受限。
2006年以来,压缩感知理论得到了各个研究领域的关注,并在声学方面得到广泛的应用和发展[6]。其中,块稀疏压缩感知是一个重要的发展方向,其恢复算法可大体分为3类:基于凸优化的块稀疏恢复算法[7]、基于块稀疏贝叶斯学习算法[8]和贪婪匹配追踪类算法[9]。
本文基于简正波理论,将浅海水平阵接收声场模型表示为声源方位空间的块稀疏信号模型,将声源方位估计问题表示为块稀疏恢复问题,基于阵元域的接收声场信号,提出一种块正交匹配追踪(Block orthogonal matching pursuit,BOMP)的浅海声源的方位估计方法,该方法属于贪婪匹配追踪类算法的一种,区别于SI方法,所提方法无需构建协方差矩阵以及特征分解估计子空间,适用于单快拍接收声场信号。BOMP方法是3类块稀疏恢复算法中原理最简单、收敛速度最快的算法[10]。通过仿真对比分析CBF和BOMP浅海声源方位估计的结果,来说明所提方法是否能准确估计靠近阵列端射方向的声源方位,并讨论信噪比的影响,最后通过海上实验数据验证所提方法的有效性。
1 块稀疏阵列信号模型与块稀疏恢复算法
考虑水平分层柱对称平坦海底的波导环境,建立水平均匀直线阵(Horizontal line array,HLA)浅海声场模型。对分析频率f,假设仅有I个远程点声源激发的声场被HLA接收,其中,第i个点源场可近似为离散的M阶简正模线性叠加[11]:
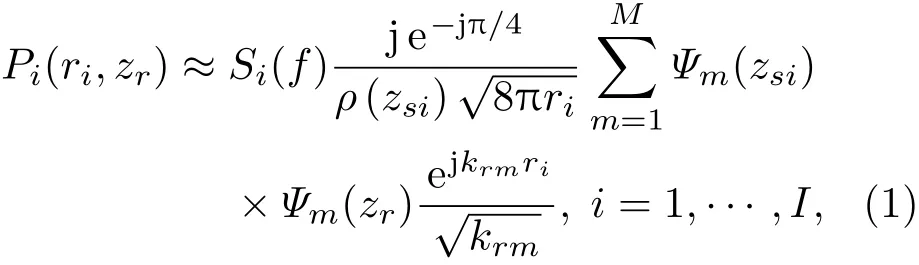
其中,Si(f)为第i个点源频谱,ri和zsi分别为对应的收发距离和声源深度,krm为第m阶简正模水平波数,zr为接收器深度,ρ(zsi)为声源处水介质密度,Ψm为模深度函数。假设HLA有L个间隔为d的阵元,第i个点源方位角为θi,以第1个阵元为参考阵元,ri表示第i个点声源与参考阵元1的水平距离,第i个点声源与参考阵元l的水平距离可表示为ril=ri+(l−1)dcosθi,假设其满足远场近似条件|ril−ri|≪ri,则第l个阵元位置的声场可近似为
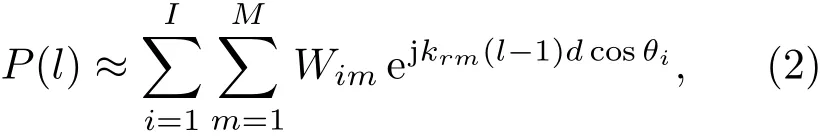
其中,
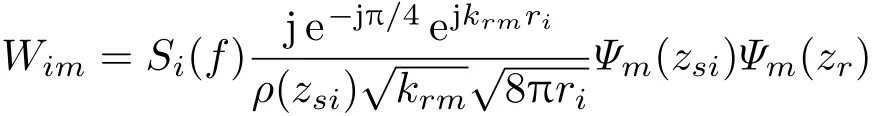
为第i个点源激发的第m阶模态,在HLA参考阵元1的位置的复数权值。公式(2)表明接收声场是I个声源激发的M阶模态线性组合的结果,共有I×M项线性求和,其中声源i激发的声信号,传播到参考阵元1位置的模态间频散体现在Wim的ejkrmri项中,声信号从阵元1传播到阵元l的模态间频散体现在ejkrm(l−1)dcosθi项中。假设已知接收深度的水介质声速为c,则波数k=2πf/c。定义第m阶简正模的俯仰角ϕm,则sinϕm=krm/k。简正波阵列信号模型如图1所示。
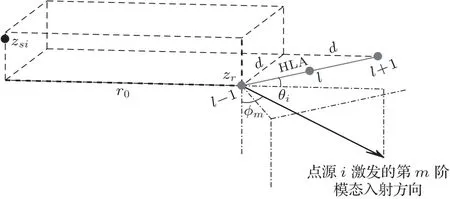
图1 简正波阵列信号模型Fig.1 Array signal model of normal mode
进一步,可将式(2)重写为
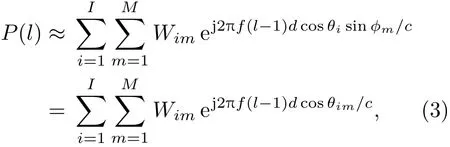
其中,θim=arccos(cosθisinϕm),对方位角θi入射的点源,将会有M个等效的模态方位角{θim}与之对应。将方位角空间{θ}进行均匀离散化,假设离散网格数为G,不考虑离格问题,认为网格中包含I个入射点源方位角,除有限I个入射点源方位角外(I一般较小),其他方位上均没有声源,因此信号是稀疏的,稀疏度为I;又因为第g个方位角对应有M个等效的模态方位角,因此信号是块稀疏的。为方便讨论,将式(3)写成矩阵的形式:

其中,y=[P(1),P(2),···,P(L)]T为测量声场向量,上标T表示转置,A∈CL×GM为按块结构组合的模态方位导向矢量矩阵(字典):
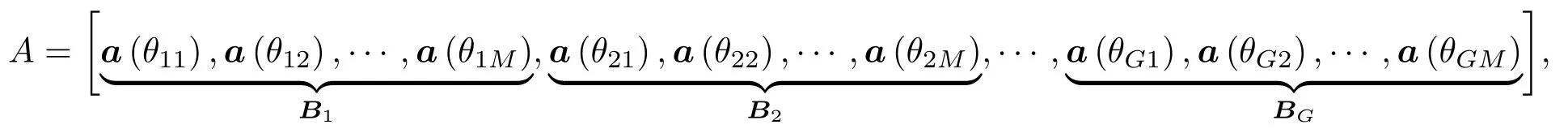
其每一列为模态方位导向矢量(原子)

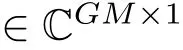

其G块中仅有I块元素非零,其余块元素均为0,n∈CL×1为测量噪声向量。此时,对浅海低频声源的方位估计问题,转化为已知测量y和模态方位导向矢量矩阵A,对权值向量x进行块稀疏恢复的问题。针对以上简正波阵列信号模型中的块稀疏恢复问题,给出BOMP声源方位估计算法,算法伪代码如表1所示。

表1 BOMP估计声源方位算法Table 1 BOMP algorithm for azimuth estimation

2 数值仿真
根据2011年北黄海声学实验中一次实测的声速剖面,并以介质均匀无限大液态海底作为仿真波导模型,如图2所示。水介质中声速接近等声速c=1480 m/s,海底声速设为cb=1650 m/s,海底深度设为H=69 m,水介质密度和海底密度分别设为ρw=1 g/cm3和ρb=1.8 g/cm3,水介质声衰减系数和海底声衰减系数分别设为αw=0 dB/λ和αb=0.1 dB/λ。仿真分析频率取f=100 Hz,使用Kraken程序[12]计算波导模态,得到4阶简正模深度函数。
2.1 两个点声源的时间方位历程图
仿真两个点声源同时做5 m/s水平匀速直线运动,运动轨迹如图3所示。声源深度均为5.7 m,源谱Si(f=100 Hz)幅度均设为1,由于声源运动速度相对水介质中声速很小,所以不考虑多普勒频移效应。同时接收阵元信噪比固定设为20 dB,即不随声源位置变化,根据图2波导环境参数,仿真计算海底HLA接收声场信号,HLA孔径设为1 km,均匀阵元间隔5 m,阵元个数为201个,使用CBF和BOMP方法分别进行声源的方位历程估计,结果如图4(a)、图4(b)所示,其中点虚线和点划线分别表示声源1和声源2的真实时间-方位历程图。图4的结果表明,CBF在对浅海低频声源方位估计时会产生波束偏移和分裂现象,特别是在靠近端射方向上,而基于块稀疏模型的BOMP算法可准确估计声源方位。

图2 仿真波导环境及100 Hz点源激发的模态深度函数Fig.2 The simulation waveguide environment and modal depth functions excited by a point source at 100 Hz
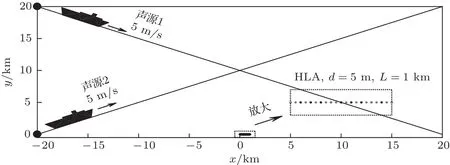
图3 两个点声源的运动轨迹和水平阵的相对位置Fig.3 The tracks of two point-sources and the relative location of HLA

图4 声源方位历程估计Fig.4 The estimation of source tracks by CBF and BOMP,respectively
2.2 信噪比的影响
为考察信噪比(Signal to noise ratio,SNR)对所提BOMP浅海声源方位估计方法的影响,仿真只考虑一个声源的情况,声源与参考阵元的水平距离为10 km,声源深度5.7 m,HLA参数与2.1小节相同,仿真声源方位分别为0°、10°、20°和30°的阵列信号,加不同的阵元SNR的复高斯白噪声,并进行1000次蒙特卡洛仿真实验,角度搜索方位为0°~90°,统计CBF和所提BOMP估计的声源方位的均值和标准差,对应误差棒曲线如图5(a)~图5(d)所示。可以看出,在声源方向靠近阵列端射方向时,CBF估计的方位角与真实的方位角存在较大的偏差,随着SNR变大,标准差变小,偏差并没有变小;随着声源方位角从阵列端射方向过渡到30°方向,CBF估计的声源方位偏差逐渐减小。通过所提BOMP方法与CBF估计结果对比发现,在SNR大于−10 dB且声源靠近阵列端射的情况下,BOMP估计的方位角与真实方位角存在较小的偏差,且随着SNR的增大,标准差减小,在高信噪比的情况下,所提BOMP方法可以实现声源方位的准确估计。在SNR小于−10 dB时,随着SNR的降低,CBF和BOMP估计的声源方位逐渐趋于0°~90°均匀分布,均值收敛于45°方向,估计的声源方位没有参考意义。由于阵元数为201,即阵增益为10lg201≈23(dB),−10 dB的阵元域信噪比对应阵列波束输出信噪比约为13 dB。实际应用时,当阵元数L已知,通过不等式SNR≥13 dB−10lgL可以判断声呐探测的海洋环境中阵元域信噪比是否符合本文方法的要求;当阵元域信噪比SNR(即输入信噪比)已知,通过不等式10lgL≥13 dB−SNR以检验声呐的线列阵阵元数L是否满足使用本文方法的要求。

图5 蒙特卡洛仿真实验1000次,统计CBF和BOMP估计的声源方位均值和标准差Fig.5 The mean and the standard deviation of the estimated source azimuth by CBF and BOMP,with 1000 times of Monte Carlo simulation experiment for each SNR
3 实验数据处理
实验数据源自2011年北黄海冬季声学实验,实验船拖曳着深度5.7 m气枪声源在准南北方向航行,航速约为4 kn,气枪间隔为1 min发射一次脉冲信号,接收阵列为海底32元准南北放置的HLA,有效阵元数为28,阵列水平孔径约250 m,通过8组邻近的气枪声信号进行孔径扩展处理[13−14],得到水平跨度为1 km、均匀阵元间隔5 m的201元HLA接收的声场信号。
对频率间隔1/3 Hz的50~200 Hz宽带声场信号(离散的频点数为451),进行逐频点声场的CBF和BOMP方位估计,其中,角度离散网格间隔取0.5°,观察角度范围取0°~40°,最大值归一化后波束输出结果如图6所示。图6(a)为CBF估计的方位谱结果,可观察到明显的波束偏移和分裂现象,每个波束峰值点并不表示真实的声源方位,由于真实的声源方位接近HLA端射方向,即方位角约为0°,分裂的波束峰对应的角度与简正模俯仰角近似互为余角关系。基于图2所示的波导模型,使用BOMP进行逐频点的声源方位估计,结果如图6(b)所示,可以看出,在大部分频点上,BOMP估计的波束输出在靠近端射方向有较强的能量。表2给出了对应451个频点估计方位角的离散统计分布。估计声源方位为0°的占比大于90%,在某些频点上出现较大的方位估计偏差,其原因包括某些频点上信噪比不足、存在干扰源影响和模型失配。图7给出了50~200 Hz宽带内波束能量求和,最大值归一化输出的结果,其中CBF波束输出旁瓣较宽,在17.5°方向上能量最大,该方向与端射方向存在较大的偏差;BOMP波束输出在0°方向能量最大,其他方位的能量只有很小的波动,与表2统计451个频点的方位估计为0°的占比大于90%结果相符,估计方位与实际声源方位一致,实验数据验证了所提BOMP方法能准确估计浅海低频宽带声源的方位。
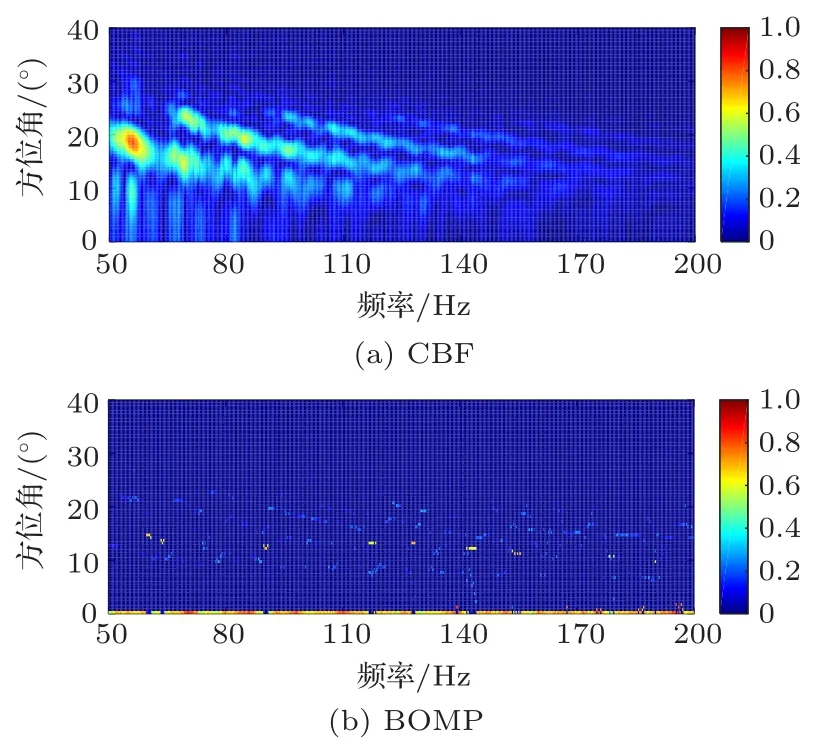
图6 实验气枪声源方位谱估计Fig.6 The experimental air-gun source azimuth spectra estimation by CBF and BOMP,respectively
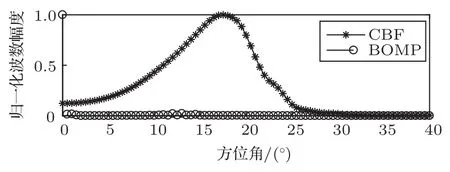
图7 实验气枪50~200 Hz宽度信号声源方位估计Fig.7 The experimental air-gun 50~200 Hz broadband source azimuth spectra estimation
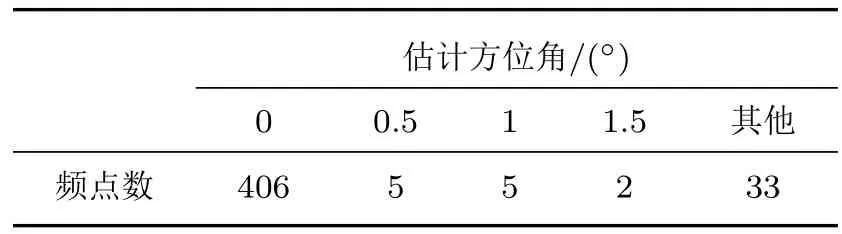
表2 统计451个频点BOMP估计的方位离散分布Table 2 Discrete distribution of source azimuth by BOMP with 451 frequency points
4 结论与讨论
本文基于浅海水平分层波导的声传播简正波理论,建立了块稀疏信号模型,提出一种块正交匹配追踪(BOMP)的浅海水平阵低频声源方位估计方法。仿真结果表明,所提方法在阵列波束输出信噪比大于13 dB和无失配环境情况下,能规避常规波束形成(CBF)方法在估计近阵列端射方向的浅海低频声源方位时所产生的波束偏移和分裂现象,从而克服较大方位估计偏差的问题。对2011年北黄海声学实验水平长线阵接收低频声信号,进行逐频点方位估计以及能量求和波束输出。CBF估计的方位谱中可以观察到明显的波束偏移和分裂现象,宽带能量求和波束输出旁瓣较宽,且波束峰值方位与真实声源方位存在较大的偏差。本文所提方法估计的声源方位除部分频点估计结果与端射方向偏离较大外,大部分频点上方位估计的结果均靠近端射方向;BOMP波束宽带能量输出,具有超低旁瓣的特点,且在0°方向取得能量值最大,与真实声源方位一致。仿真和实验数据验证了所提方法的有效性和较CBF的优越性。
本文所提BOMP算法需要已知波导环境参数,用于计算模态方位导向矢量矩阵字典,当环境参数存在失配,特别是在较高频段,声源方位的估计偏差会变大,在实际应用中需要选择合适的等效波导环境参数。另外,本文所提方法针对大孔径基阵近端射声源方位估计中存在的波束分裂和方位偏差问题,只适用于较高信噪比的水平阵信号,当信噪比不足时,估计的声源方位会出现较大的偏差。
致谢感谢参加2011年北黄海冬季声学实验的全体工作人员,他们的辛苦工作为本文提供了宝贵的实验数据。

