浅海近程混响的振荡现象∗

殷丽君 吴金荣 侯倩男

(1中国科学院声学研究所 中国科学院水声环境特性重点实验室 北京 100190)

(2中国科学院大学 北京 100049)

0 引言

浅海混响主要是由海底散射引起。混响强度振荡现象已经在不同的混响实验中被观测到，Cole等[1]将一种混响强度在时域上表现出的振荡模式类比于洛埃镜效应，随着声源脉宽增加，这种混响强度振荡现象会逐渐减弱并消失。Yang等[2]将一次混响实验中发现的混响强度振荡现象与海底地形起伏联系起来，其中混响强度峰值来源于地形突出部分的散射作用，混响强度谷值则是地形凹陷部分的散射作用。为研究混响强度及其衰减规律与脉宽的关系，苏哈列夫斯基[3]验证了短脉宽下远程混响强度与脉宽成正比，在此基础上，裘辛方[4]指出近程混响的饱和趋势不仅取决于苏哈列夫斯基所指出的波阵面扩展和海水吸收，也与散射界面或散射层的掠射角特性及收发换能器的垂直指向性有关。此外，吴金荣等[5]通过数值计算发现影响浅海近程混响衰减规律的主要因素是海底散射特性，海底倾斜角对混响平均强度衰减特性影响较小。

2015年和2016年在南中国海进行的两次浅海混响实验均发现了稳定的混响强度振荡现象。实测混响数据结果显示，随时间推移和声源脉宽改变，混响强度幅值及振荡周期保持不变，这与文献[1-2]所揭示的混响振荡现象有所差异。此外，两次实验得到的混响强度振荡周期几乎是一致的，由于两次实验海深及收发深度相近，且振荡周期与相邻散射路径在海底与海面之间垂向往返的时延一致，为此，本文猜测这一现象与短距离内的声线多途有关。为分析浅海近程混响信号结构及其特性，本文在射线理论基础上给出了一种浅海近程混响模型，其中，小斜率近似用来计算海底粗糙界面散射过程。

1 实验现象

在2015年和2016年，中国科学院水声环境特性重点实验室的研究人员在南中国海较为平坦的浅海海区进行了两次单站混响实验。两次实验期间测得海区声速剖面在图1中给出，两海域深度分别为88 m和86 m，收发深度均为32 m，发射声源均为不同脉宽的260 Hz单频信号。

图1 实测声速剖面Fig.1 Sound pro file measured during experiment

图2和图3分别给出了2015年和2016年两次海试测得的混响结果，每条混响强度曲线经1/3倍频程宽带滤波、20 ms时间窗平滑和20组接收信号平均处理后得到。从图2可以看出，2015年混响实验的声源脉宽分别为0.1 s、0.5 s和2 s，0.28 s之前的混响强度衰减趋势存在稳定的振荡现象，随时间推移混响强度振荡周期保持不变，且脉宽对这一振荡模式影响不大，在0.28 s之后，随着混响强度减小，振荡现象不明显。文献[1]指出声源脉宽变宽，散射声场相干叠加形成的混响强度起伏现象逐渐消失，由此可以确定本文实验中观察到的振荡现象不是由散射能量相干叠加造成的。图3给出了2016年实验中测得的脉宽分别为0.1 s、0.5 s、2 s和4 s对应的混响强度时间序列，可以从中发现与图2给出的混响强度类似的特性。图4将两次混响实验中0.5 s脉宽声源对应的混响强度求导结果进行比对，通过对比可以发现，由于两次混响的实验环境不同，2016年测得混响强度衰减速度明显快于2015年，相应地，2016年测得的数据结果中稳定振荡现象的持续时间相对较短，图3中0.14 s之前可以发现稳定的振荡现象，在0.14 s之后，这一稳定的振荡规律开始消失。从图4可以看出，在0.14 s之前观察到的混响强度振荡周期是基本吻合的。两次混响实验的测量环境不同，参照文献[2]给出的地形起伏对混响强度衰减趋势的影响，说明本文实验中发现的振荡现象不是由海底地形振荡造成的。

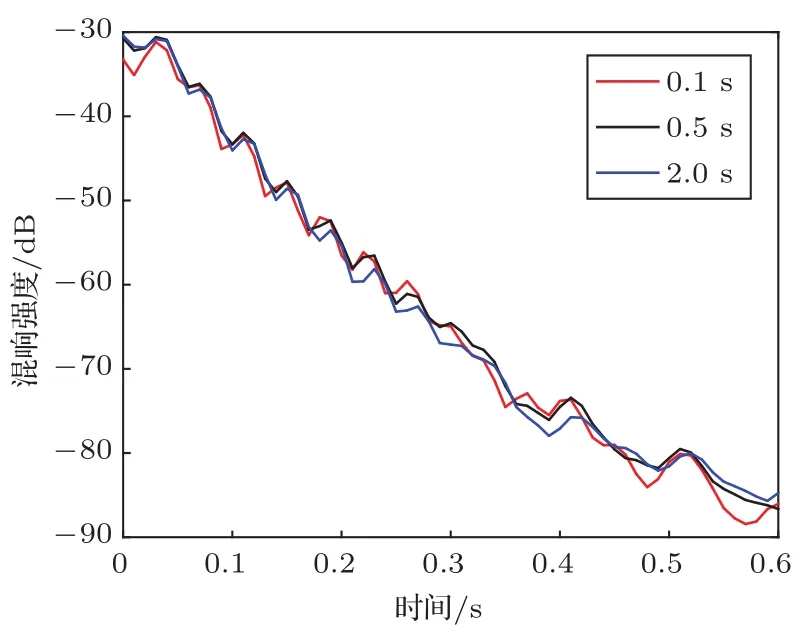
图2 2015年测得的不同脉宽声源对应的混响强度时间序列Fig.2 Reverberation level time series for different pulse lengths measured in 2015

图3 2016年测得的不同脉宽声源对应的混响强度时间序列Fig.3 Reverberation level time series for different pulse lengths measured in 2016

图4 两次实验中脉宽0.5 s声源对应的混响强度求导结果比较Fig.4 Comparison of the derivation results for reverberation intensity with pulse length of 0.5 s during the two experiments

2 振荡现象的物理解释

2.1 小斜率近似

本文研究的混响是浅海单站混响实验中直达信号之后紧随的近程混响信号，这段混响主要由粗糙海底近垂向大掠射角散射声场组成，实验海区海底地形平缓。对于坡度足够小的粗糙界面，小斜率近似在不损失传统近似精度的基础上给出覆盖全掠射角范围的散射模型，其散射模型对应的散射截面可表示为[6]

对于半无限均匀液态海底模型，

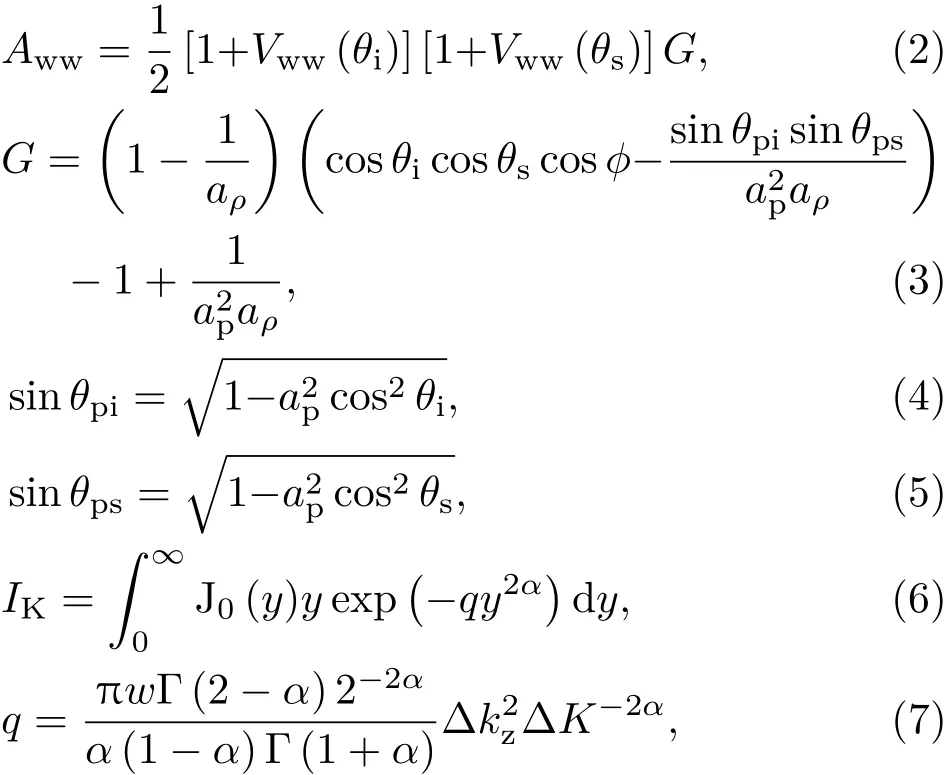
这里ΔK和Δkz分别为散射波数与入射波数的水平分量之差和垂向分量之差，θi为入射掠射角，θs为散射掠射角，ϕ为入射水平方位角和散射水平方位角之差，Vww(θ)是以掠射角θ入射到平坦界面的反射系数，aρ为海底沉积层密度和水体密度的比值，ap为沉积层声速与水体声速的复数比值，J0为零阶一类Bessel函数，Γ为伽玛函数，α与边界粗糙谱指数γ之间关系为α=γ/2−1，w为谱强度。

2.2 混响模型

在实验现象分析过程中排除了散射声场相干叠加对混响强度振荡衰减的影响，因此在混响计算过程中选择采用散射声场非相干叠加的形式进行。这里考虑的浅海单站混响问题如图5所示，海水和海底均视为均匀半空间，某一时刻的混响强度为海底各散射元产生并同时到达接收点的散射声强的叠加。为分析近程海底混响形成过程，图中从左至右给出了单条散射路径的海底散射区域随时间的变化过程，可以看出，声信号刚传到海底时，海底开始形成圆形散射区域且半径逐渐增大，在脉宽为τ的信号完全入射到海底的时刻散射区域开始变成圆环，并随时间推移逐渐向外扩展。

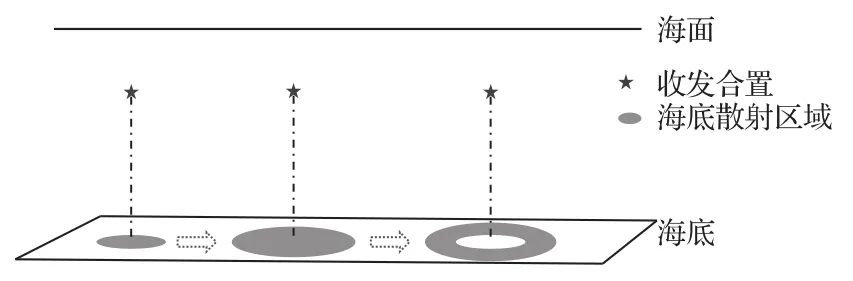
图5 单站海底混响形成示意图Fig.5 Scenario of bottom reverberation in the monostatic case

根据回射声线路径和出射角方向，本文考虑的海底散射路径分为4组，如图6所示：(a)出射角向下的声线经若干次界面反射后直接由海底散射返回接收点；(b)出射角向上的声线经若干次界面反射后直接由海底散射返回接收点；(c)出射角向下的声线经若干次界面反射后由海底散射返回接收点的过程中被海面反射一次；(d)出射角向上的声线经若干次界面反射后由海底散射返回接收点的过程中被海面反射一次。

图6 单站混响散射路径Fig.6 Scattering paths in the monostatic case

假设时刻t共有M条散射路径对混响有贡献，将海底散射区域宽度为Δr的圆环进行离散，则时刻t路径m(m=1,2,···,M)在粗糙海底界面上对应一组散射环rm，忽略水体吸收的影响，海底平均混响强度表示为各路径海底散射能量的非相干叠加形式：

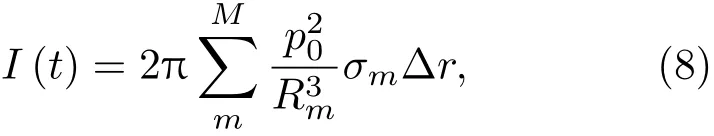
其中，p0为声源声压，σm和Rm分别为路径m对应的海底散射截面和声源与散射微元间水平距离。

3 混响强度特性仿真分析

环境参数与2015年实验相同，考虑散射路径垂向入射到粗糙海底的情况，相邻路径之间时延约为0.04 s，这与实测混响振荡周期一致，因此假设混响强度的振荡现象与到达接收点散射声场的声线多途有关。为进一步验证及分析近程混响强度特性，本节数值仿真所用参数如下：无指向性单频声源频率260 Hz，接收水听器无指向性，收发深度32 m，海深88 m，水体声速1530 m/s，密度1000 kg/m3。参照混响实验海区海底沉积层测量结果，利用半无限大第二类海底[6]仿真计算混响强度，海底为半无限大第二类海底[6]，其声速1753 m/s，密度1970 kg/m3，粗糙界面谱指数γ2=3.3，谱强度w2=0.001 m0.7。

0.1 s、0.5 s、1 s脉宽对应的混响强度衰减规律仿真结果如图7所示，其中起始时刻从发射脉冲结束时算起，由图可以看出，混响强度振荡周期随时间推移保持不变，此外，脉宽的改变对近程大掠射角散射形成的混响强度衰减规律几乎没有影响。这是因为近程混响强度由近垂向大掠射角海底散射声场主导，也就是说，来自图5海底散射区域内环部分的散射能量主导近程混响强度的振荡规律，虽然脉宽越长，某一散射路径能够在海底形成的散射区域面积越大，但由于外环部分对应的小掠射角散射对近程混响强度的影响是可以忽略的。所以，混响强度第一个峰值的出现是由于直达海底散射路径(图6中路径1)的近垂向大掠射角散射声场到达接收水听器，在路径1对应的海底散射区域由圆开始拓展为圆环的时刻，散射掠射角开始减小，混响强度迅速衰减，随后的混响强度衰减规律以相同的原理周期性出现。

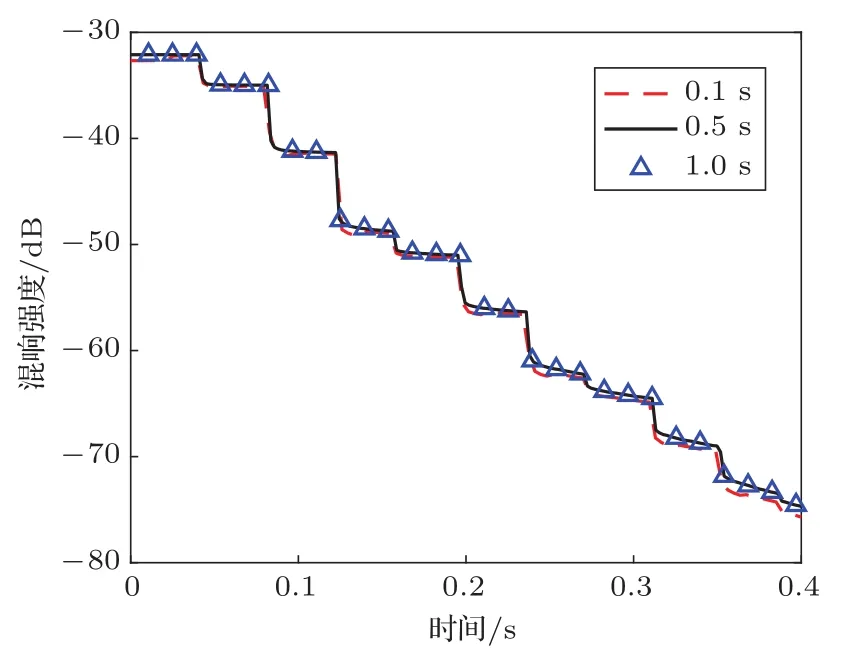
图7 仿真不同脉宽声源所得混响强度结果Fig.7 Reverberation level calculated using the model with different pulse lengths

图8给出了声源脉宽为0.1 s时，采用2015年海洋环境参数的数值模拟结果与2015年实测混响数据的对比图，模型预报结果与实测数据吻合较好，验证了混响模型选取的合理性，也证明了近程混响强度振荡周期为相邻散射路径在海底和海面间垂向往返的时延，振荡周期与图6中(a)(b)间或(c)(d)间相邻散射路径的关系可表示为T=2zs/c，振荡周期与(d)(a)间相邻散射路径关系可表示为T=(2H−4zs)/c。

图8 脉宽0.1 s时数值模拟结果与实测混响强度对比图Fig.8 Measured reverberation level versus corresponding model predictions for a pulse length of 0.1 s

4 结论

为分析浅海近程混响强度振荡现象，本文基于射线理论及小斜率近似给出浅海近程混响模型，并仿真模拟海底倾斜度对近程混响强度的影响，主要结论如下：

(1)近程混响强度的振荡现象是由声线大掠射角散射声场到达接收位置的时延造成的，由此说明对于浅海近程混响，声线多途效应不可忽略，实验与数值结果的吻合验证了混响模型的合理性，由此给出的混响强度振荡周期与海深、收发深度的关系，可作为指导抑制近程混响，提高主动声呐探测性能的理论判据。

(2)粗糙海底散射强度与掠射角的关系随海底界面及沉积层特性的改变而有所差异，混响强度振荡幅度与海底近垂向大掠射角散射强度呈正相关，由此可知，近程混响振荡现象会随海底散射特性的变化而增强、减弱或消失。