湍流边界层激励下高速列车车窗参数研究∗

潘爱鹏 李 晔 张学飞 王瑞乾

(1常州大学机械与轨道交通学院 常州 213164)

(2西南交通大学牵引动力国家重点实验室 成都 610031)

0 引言

近年来，轨道列车得到了快速发展。从1997年至今，中国铁路经历了6次提速，部分线路的列车运行速度超过250 km/h，时速高于160 km/h的线路近万公里，且建成“四纵四横”客运专线。然而，随着高速铁路运行速度不断提升，一些在低速运行时被忽略的问题逐渐受到关注。其中，列车噪声随着车速提高而明显升高，成为亟待解决的问题之一[1]。高速列车内部噪声问题有一部分源于外部流体产生的湍流边界层(Turbulent boundary layer,TBL)，其直接作用于车体外表面进而影响了车内声场环境。车窗作为高速列车车体重要组成部分，其声振特性备受关注。因此，对在TBL激励作用下车窗振动响应的正确预测，对于减小车窗结构辐射噪声至关重要[2]。

已有大量研究对平板在TBL激励下的振动响应展开预测。Strawderman[3]对当时现存的湍流下的有限板和无限板模型的预测结果进行了总结，结果表明：尽管有限板和无限板模型的预测结果都不完全与试验结果一致，但是相比于无限板件，有限板件的预测结果能更好地符合试验结果。Ichchou等[4]提出了一种雨点激励模型，该模型主要用来描述作用于平板上的点激励，其在中频区域与用有限元模型计算的结果吻合较好。Ciappi等[5]对复合材料板进行了理论和实验研究，其结果显示在高马赫数时，复合材料板的流体加载效应不可忽略。Rose等[6]针对湍流激励下线性系统的动态响应的求解提出了一种伪确定性激励方法，该方法大大缩短了计算时间。Franco等[7]提出了平板振动响应在TBL激励下的相似规律，这些规律消除了由于流动速度、尺寸和材料特性的变化而需要重复试验或者数值模拟的必要性。由于TBL激励为随机激励，而平板结构在该激励下的振动响应通常是通过大量的频响函数推导出来的[8]，对计算资源要求较高且耗时。为了解决这个问题，有研究提出在波数-频率域内将TBL表示为一组非相关壁面平面波，并以此来模拟壁面压力的方法[9−10]。该方法把非相关壁面平面波多次模拟的壁面压力结果进行综合平均以得到最接近TBL激励下的壁面压力，并将获得的壁面压力加载到平板的有限元模型表面，从而求解得到整个平板的声振响应。

本文通过应用混合非相关壁面平面波技术-有限元方法，研究了空腔厚度、双侧玻璃厚度比以及空腔阻尼损耗因子3个参数变化对高速列车车窗声振特性的影响。

1 车窗壁面压力的获取

在高速列车运行过程中，由于结构表面的不平整性，车窗结构会受到TBL的激励而产生振动。由于TBL激励仅直接作用于车窗外侧玻璃，故在获取车窗壁面压力阶段将车窗的双板空腔模型简化为某一单板，尺寸材料参数均按车窗外侧玻璃设定。车窗外侧玻璃表面受到的TBL激励如图1所示，假设TBL激励均匀稳定地完全作用于车窗表面并且TBL激励引起的壁面压力不受车窗振动的影响。

图1 TBL激励下车窗结构Fig.1 Windows of high speed trains under TBL

非相关壁面平面波技术由Maxit[9]提出用来模拟TBL激励下的壁面压力场，该方法主要分为3步：

(1)给出TBL激励下壁面压力的空间-频率域的互谱密度(Cross-spectral density,CSD)函数。

(2)给出一组非相关壁面平面波作用下壁面压力的空间-频率域的CSD函数。

(3)用非相关壁面平面波作用下的CSD函数表示TBL激励作用下的CSD函数。

TBL激励作用下壁面压力在空间-频率域下的CSD函数可表示为

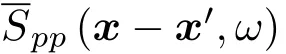
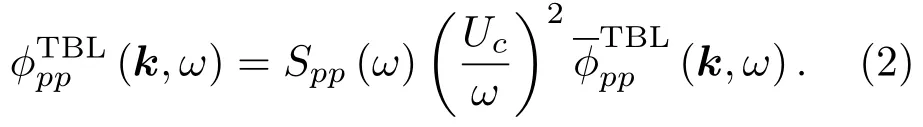
壁面压力的ASD函数可用Goody半经验模型来表示，因此Spp(ω)表示为

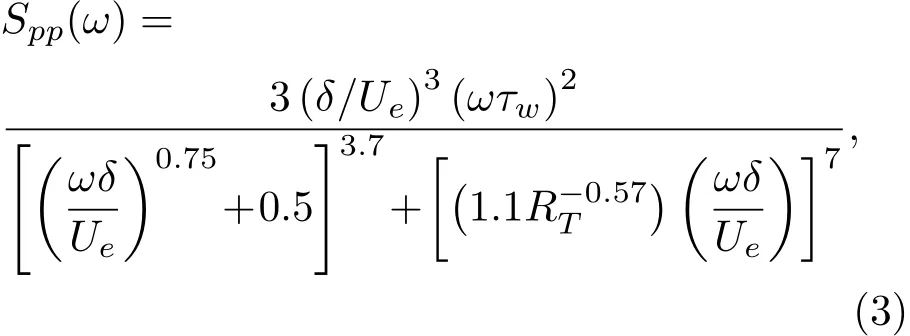
壁面压力的归一化CSD函数可由Corcos模型来表示，其在波数域内表达式为

式(4)中，归一化CSD函数在流向和展向的指数衰减系数分别为αx=0.1和αy=0.77。

空间-频率域下的CSD函数与波数-频率域下CSD函数有如下关系：

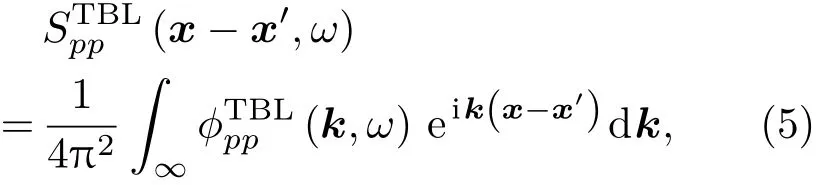
式(5)中，i表示虚数单位。由于公式(5)中二重反常积分存在于波数-频率域内，在指定频率下，对该二重积分采取矩形截断求和方法进行等效。因此，公式(5)可近似如下：

式(6)中，Δkx、Δky分别表示流向和展向对应的波数分辨率，取值为Δkx= Δky=0.25 rad/m；Nx、Ny表示流向和展向截断的个数。

壁面平面波只在板的表面被定义，因此壁面平面波是一个表面波。假设某一壁面平面波作用下结构表面的壁面压力为

其壁面压力对应的空间-频率域下的CSD函数表示为

式(8)中，SAA(ω)是波振幅的ASD函数。

假设壁面平面波之间互不相关，当出现若干壁面平面波时，其对应的一组壁面平面波的CSD函数表示为

当定义壁面平面波振幅的ASD函数为公式(10)时，即

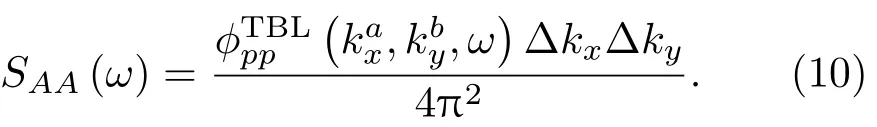
将公式(10)代入公式(9)时得到一组非相关壁面平面波作用下的压力CSD函数为

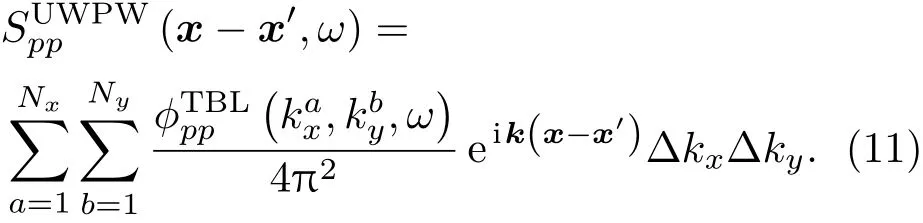
至此，TBL激励下的壁面压力CSD函数等于一组非相关壁面平面波作用下的壁面压力CSD函数。即当壁面平面波的振幅为公式(10)时，TBL激励下壁面压力可以由一组非相关壁面平面波下壁面压力表示。此方法将TBL激励的壁面压力表示为输入，可以与有限元模型进行耦合来计算结构振动响应。

由一组非相关壁面平面波模拟的在节点n处的第m次壁面压力可表示为

将公式(10)带入公式(12)，并结合公式(2)～(4)，对于有限元模型上节点n，其在第m次模拟的壁面压力为

式中：x和y代表在流向和展向的坐标轴，(kx,ky)代表各个壁面平面波的波数域下坐标，(xn,yn)代表节点坐标，Δkx和Δky代表流向和展向的波数分辨率，代表随机相位，属于[0,2π]。由公式(13)，以表1中的车窗外侧玻璃参数和外流体参数为输入，对计算获得的多次壁面压力进行综合平均后得到了300 km/h时速下高速列车车窗在TBL激励下的壁面压力，其中图2给出了200 Hz对应的壁面压力图。

表1 车窗外侧玻璃参数和外流体参数Table 1 Window parameters and fluid parameters

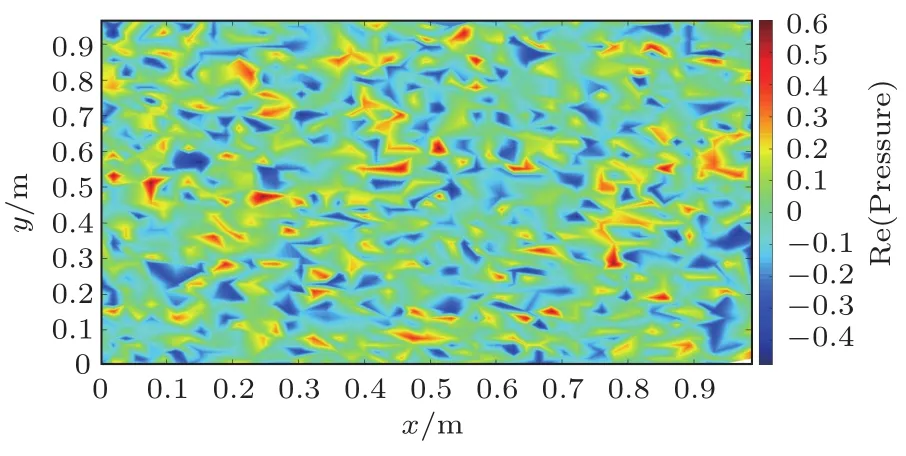
图2 高速列车车窗200 Hz下壁面压力Fig.2 Wall pressure of windows on high speed trains under TBL

2 车窗声振特性及参数研究

通过声振分析软件建立了我国某高速列车车窗在TBL激励下的声振响应预测模型。首先建立了内外侧玻璃的有限元模型，单元类型为2D壳单元，网格大小为19 mm，共有5304个2D壳单元。基于车窗内外侧玻璃的有限元模型在声振分析软件中拉伸出内外侧玻璃之间的空腔，对该空腔结构也进行了网格划分，单元类型为3D实体单元。将车窗玻璃与空腔进行连接形成完整的车窗结构。在内侧玻璃旁车厢内以垂直于车窗的形式建立半径大小为1 m的半圆形声音辐射接收面a用以探究辐射声音的强弱和分布随距离的变化而产生的变化，并且在距离内侧玻璃0.3 m处设立传感器用以模拟乘客在此处接收到的声压值。将其边界条件设为简支状态[13]，其建立的预测模型如图3所示。表1中给出了在壁面压力获取阶段所需要的车窗外侧玻璃参数，内侧玻璃厚度为4 mm，其余参数与外侧玻璃一致，双侧玻璃阻尼损耗因子均为0.005，空腔厚度为16 mm，空腔阻尼损耗因子为0.05[13]。基于上述模型，分别研究了空腔厚度、双层玻璃厚度比以及空腔阻尼损耗因子这3个参数对车窗在TBL激励下声振响应的影响。

图3 车窗结构有限元模型Fig.3 Finite element model of windows on high speed trains under TBL

2.1 空腔厚度对车窗声振响应的影响

保持车窗其他参数不变，将空腔厚度分别调整为8 mm、12 mm、16 mm、20 mm和24 mm共计5个工况。其中，16 mm为我国某高速列车车窗空腔厚度。图4给出了内侧玻璃的平均速度响应，图5给出了内侧玻璃辐射声功率级，图6给出了距离内侧玻璃0.3 m处的声压级，图7给出了内侧玻璃的辐射效率。

图4 内侧玻璃平均速度响应Fig.4 Average velocity response of inside glass

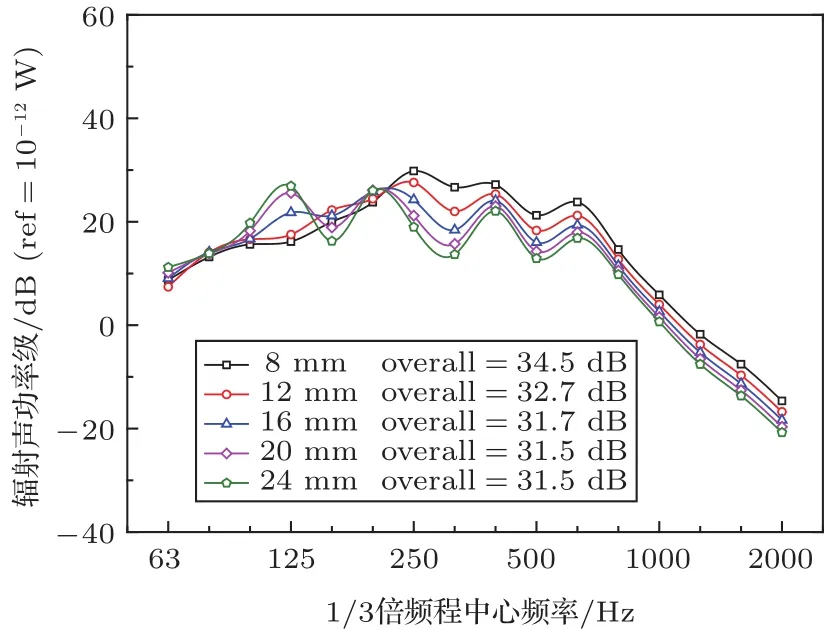
图5 内侧玻璃辐射声功率级Fig.5 Radiated sound power level of inside glass

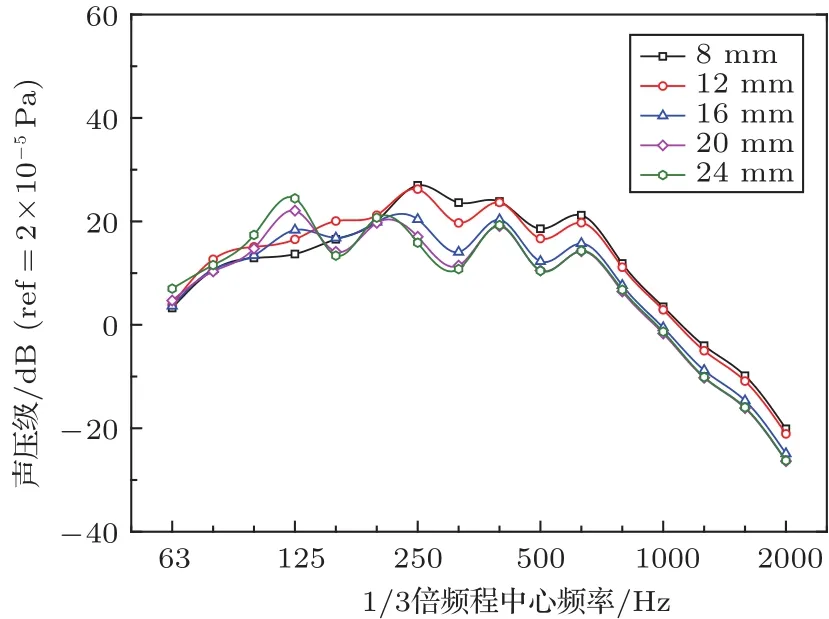
图6 距离内侧玻璃0.3 m处的声压级Fig.6 Sound pressure level at 0.3 m from the inside glass

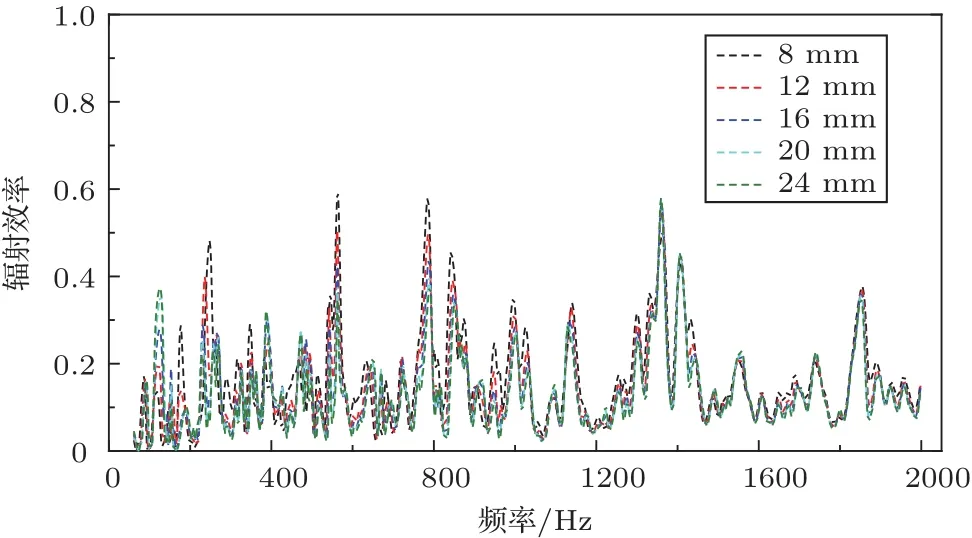
图7 内侧玻璃辐射效率Fig.7 Radiationefficiency of inside gla

由图4～图6可知，在保持其他参数不变的情况下，绝大部分频率下的平均速度响应、辐射声功率级和声压级都随着空腔厚度的增加而降低。但是在低频某些频率处，却出现了相反的声振规律，如在125 Hz下，空腔厚度越厚，辐射声功率级和声压级反而变大：125 Hz下5种工况的平均速度响应差别不大，图7中发现该频率下辐射效率遵循着空腔厚度越厚，辐射效率越高的规律。结合两者将其反映到图5和图6中表现为5种工况下辐射声功率级和声压级在该频率下存在明显差距，且空腔厚度越厚，计算出的辐射声功率级和声压级越大，对于该特例的产生机理还有待深入探究。5种工况下的声压级在中高频阶段随着频率的增加而降低，主要是由于在中低频下的壁面压力整体要大于高频阶段的壁面压力，且频率越高壁面压力越小。当空腔厚度小于16 mm时，各个工况下的声压级在中高频阶段相差无几；当空腔厚度达到16 mm时，其声压级与之前工况相比有较大衰弱，衰弱了3～5 dB。无论是从辐射声功率级总值还是0.3 m处的声压级来看，空腔厚度为20 mm和24 mm时数值均无明显变化。因此，取空腔厚度为20 mm，可使车窗结构在TBL激励下的声振响应削减最显著，且符合空间节省原则。

2.2 双侧玻璃厚度比对车窗声振响应的影响

保持其他参数不变，将外侧、内侧玻璃厚度比分别调整为1:1、3:1、5:2、7:3和9:5共计5个工况，其中5:2为我国某高速列车车窗外侧、内侧玻璃厚度比。图8给出了5种工况下内侧玻璃的平均速度响应，图9给出了内侧玻璃的辐射声功率级。

图8 内侧玻璃平均速度响应Fig.8 Average velocity response of inside glass

由图8可知，在低频阶段，9:5下的平均速度响应要低于其余4种工况，3:1下的平均速度响应走势起伏变化较大，其余3种工况下平均速度响应则比较接近。而在中高频阶段，除了1:1外，其余4种工况的平均速度响应差距不大，且1:1下的平均速度响应明显高于其余4种工况。图9中除1:1外的4种工况的辐射声功率级在分析频带内都较为接近；1:1时在低频阶段走势起伏变化较大，到了高频阶段，与其余4种工况差距明显且明显高于其余工况。图9中根据分析频带内的辐射声功率级计算了各个工况下的声功率级总值，可以发现比例为1:1时，声功率级最大，3:1的声功率级次之，7:3和9:5比较接近。由于辐射声功率与振动功率成正比，随着频率的增加，高频阶段的壁面压力逐渐降低，声功率级也呈现逐渐降低趋势。1:1比例下内侧玻璃在1601 Hz存在显著模态，因此在1600 Hz下速度响应和辐射声功率都出现了波峰。图10给出了5个工况下声音辐射接收面a的声压总值分布，由图能清晰看出声压分布遵循着由中心往外逐步扩散降低的特征。通过对比发现9:5下的声压值最低，由左往右依次增加，符合辐射声功率级的总值规律。因此，在计算的5种工况下，9:5作为车窗双侧玻璃厚度比最合适。

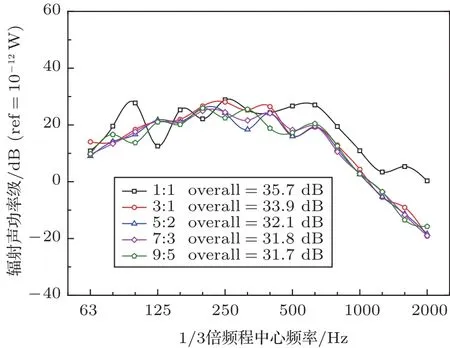
图9 内侧玻璃辐射声功率级Fig.9 Radiated sound power level of inside glass

图10 各个工况下分析频段内声音辐射接收面a的声压总值Fig.10 The total sound pressure value of the surface a in the full frequency band under various working conditions

2.3 空腔阻尼损耗因子对车窗声振响应的影响

保持车窗其他参数不变，将空腔阻尼损耗因子调整为0、0.005、0.01、0.05和0.08共计5个工况。其中我国某高速列车车窗空腔阻尼损耗因子约为0.05[13]。图11给出了内侧玻璃的平均速度响应，图12给出了内侧玻璃的辐射声功率级，图13给出了距离内侧玻璃0.3 m处的声压级。

由图11可知，随着空腔阻尼损耗因子的增加，内侧玻璃的平均速度响应逐渐降低；低频阶段，5种工况下速度级响应比较接近，随着频率的增加，高频阶段的差距逐渐拉大。通过计算图12中5种工况下分析频带内的辐射声功率级总值，当阻尼从0.01增加到0.05时，辐射声功率级总值降低幅度是最大的，总值降低了2.8 dB；阻尼从0增加到0.005时，辐射声功率级总值降低幅度次之，总值降低了1.2 dB；阻尼从0.005增加到0.01和从0.05增加到0.08时，辐射声功率级总值变化不明显，总值分别变化了1 dB和0.7 dB。当这种变化表现到图13声压级上时，可以发现在阻尼从0增加到0.005和阻尼从0.01增加到0.05这两种辐射声功率级总值变化比较大的工况下，声压级在高频阶段有了明显降低，剩余的两种阻尼变化情况下，声压级在低频和高频阶段几乎相等，中频阶段有细微的差异。考虑到制造成本的因素，当空腔阻尼损耗因子为0.05时，最适合作为高速列车车窗结构的参考值。

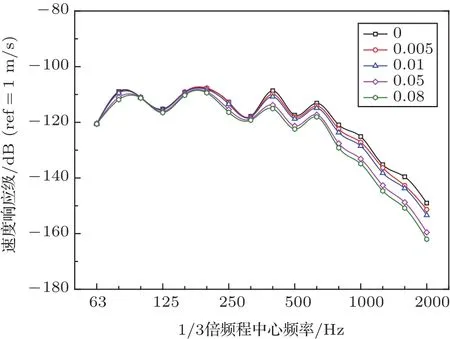
图11 内侧玻璃平均速度响应Fig.11 Average velocity response of inside glass

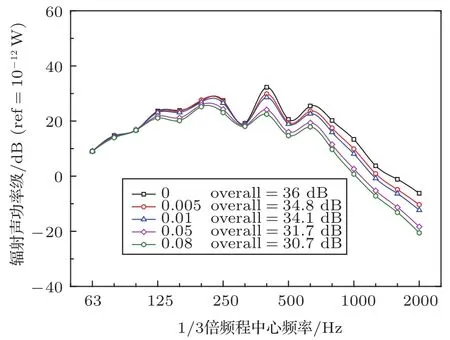
图12 内侧玻璃辐射声功率级Fig.12 Radiated sound power level of inside glass

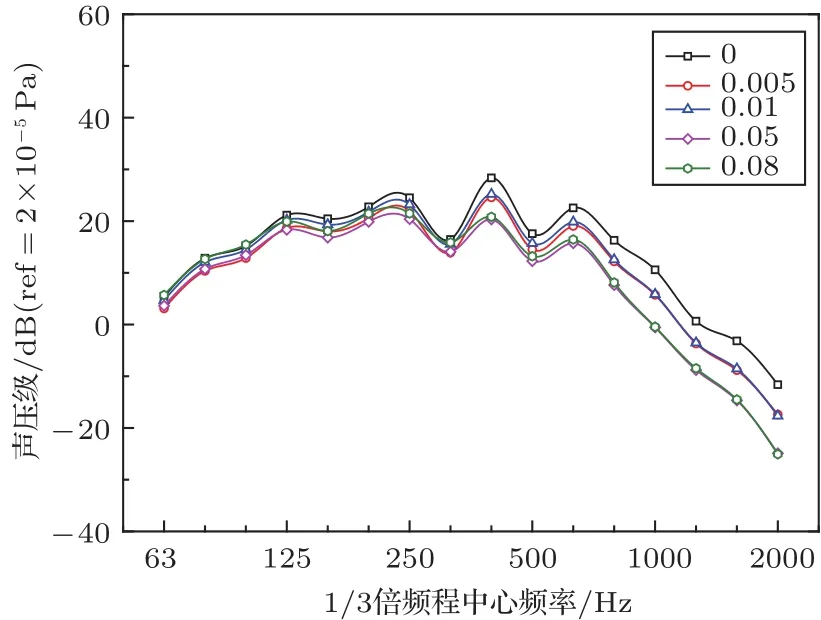
图13 距离内侧玻璃0.3 m处声压级Fig.13 Sound pressure level at 0.3 m from the inside glass

2.4 高速列车车窗的声振性能优化

由前文所研究的3个参数的仿真预测结果可知，当空腔厚度为20 mm、双侧玻璃厚度比为9:5、空腔阻尼损耗因子为0.05时分别为各自研究参数下工况中的最合适解。基于参数研究的结果，对我国某高速列车车窗结构提出声振性能优化方案：将原车窗空腔厚度调整为20 mm，双侧玻璃厚度比调整为9:5，空腔阻尼损耗因子保持不变，其他材料参数不变。基于此种方案下，建立优化后的车窗预测模型，并与原车窗声振响应进行对比，对比结果如下：W1代表优化后的车窗声振结果，W2代表的是我国某高速列车车窗结构的声振结果，图14给出了内侧玻璃平均速度响应，图15给出了内侧玻璃辐射声功率级，图16给出了内侧玻璃的辐射效率。

由图14和图15可知，在分析频带内优化后的内侧车窗玻璃的平均速度响应和辐射声功率级均低于优化前的声振响应结果。通过计算对比，发现优化后车窗结构的辐射声功率级总值较优化前降低了2.8 dB。由于优化后的车窗结构固有频率发生改变，在315 Hz处振型明显，而优化前车窗结构在此频率下并非固有频率，因此导致该频率下平均速度响应和辐射声功率级偏大。由图16可见在大部分频率区间内，特别是中低频阶段，优化后的车窗辐射效率较优化前明显降低。

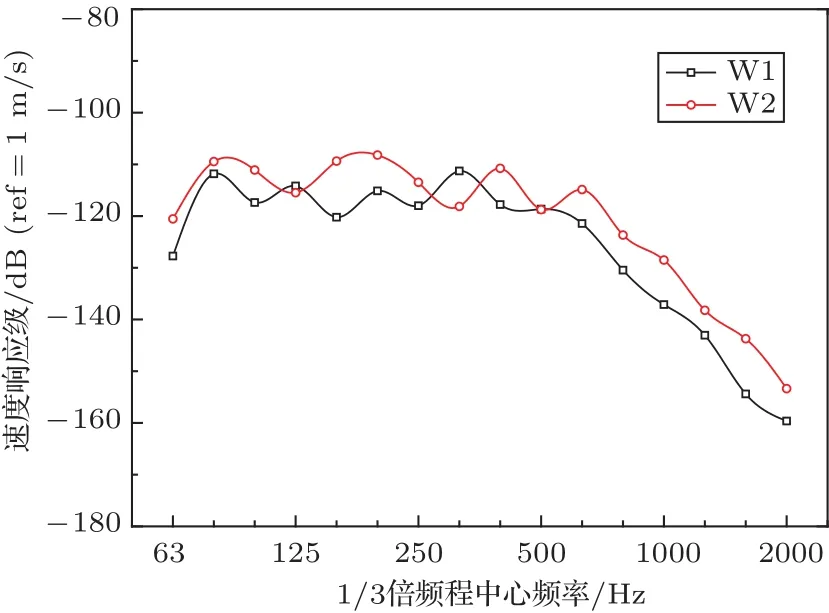
图14 内侧玻璃平均速度响应Fig.14 Average velocity response of inside glass

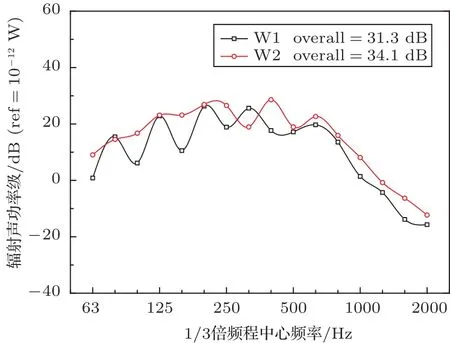
图15 内侧玻璃辐射声功率级Fig.15 Radiated sound power level of inside glass

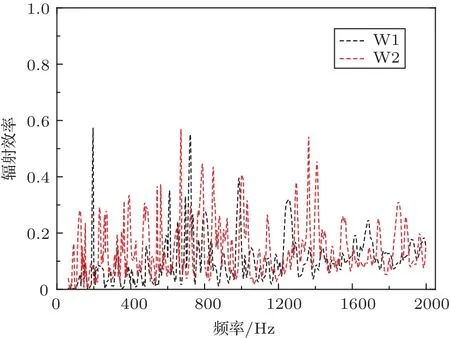
图16 内侧车窗玻璃的辐射效率Fig.16 Radiation efficiency of inside glass

3 结论

将非相关壁面平面波技术和有限元模型进行结合，在声振分析软件中建立了高速列车车窗在TBL激励下的仿真预测模型。研究了空腔厚度、双侧玻璃厚度比和空腔阻尼损耗因子对车窗在TBL激励下声振特性的影响，并基于研究结果对现有车窗结构进行了优化，结论如下：

(1)随着空腔厚度的增加，车窗结构的声振响应逐渐减弱。综合考虑对车内声场环境优化效果和空间节省原则，选定20 mm的空腔厚度作为优化方向之一。

(2)改变双侧玻璃厚度比是在不增加结构整体质量情况下，减小车窗结构向车内辐射噪声的一种有效办法。在达到优化车内声场环境的目的下，未改变结构质量，满足了轻量化设计要求。在调查的工况中，当外侧、内侧玻璃厚度比为9:5时，车窗声振响应的优化效果最好。

(3)基于参数调查结果对车窗结构提出优化方案，优化后的车窗结构在辐射声功率级总值上较原车窗降低了2.8 dB。在分析频段内除了个别频率点外，声压级都得到了降低。

综上，本文所做的参数研究结果对于高速列车车窗在TBL激励下的声振特性优化具有一定的参考价值，对于高速列车上其他车体板壁结构在TBL激励下声振性能的研究有一定的借鉴意义，同时对提高设计开发效率和降低生产成本起到了积极作用[14]。