经颅聚焦超声联合微泡开放血脑屏障的数值仿真研究

潘 婷 孙天宇 张艳秋 张默涵 凌子超 菅喜岐

(天津医科大学生物医学工程与技术学院 天津 300070)

0 引言

血脑屏障(Blood-brain barrier,BBB)是介于血液和脑实质之间的保护性屏障[1−2]，对维持大脑内环境稳态至关重要。但当颅内脑组织发生如脑肿瘤、中风、帕金森氏病、阿尔茨海默症等病变时，BBB将阻碍治疗药物进入脑组织[3]。为了使药物进入脑组织发挥其疗效，目前已有多种跨越BBB递送药物的方法[4−8]，如循环系统外递送、跨细胞转运、改变细胞旁通路转运和纳米药剂等，但这些方法或效率有限，或副作用大，有必要探索安全、高效的BBB开放方法实现药物的有效递送。

1955年，Barnard等[9]发现高强度超声可引起BBB通透性改变，但稳定性差，易引发脑组织损伤。2001年，Hynynen等[10]发现脉冲聚焦超声(Focused ultrasound,FUS)与超声造影剂结合能可逆地破坏局部BBB，且未引起神经元损伤。2010年，Madsen等通过动物实验表明该方法可无创、靶向、重复可逆开放BBB[11−15]。2016 年，Kobus等[16]使用FUS联合微泡反复诱导大鼠BBB开放，研究表明重复开放对大脑组织无损伤或仅在较高声压下出现微出血等轻微不良反应。尽管FUS联合微泡介导BBB开放的机制尚不清楚，但与微泡在声场中空化行为密切相关。机械指数(Mechanical index,MI)是评估BBB开放程度及组织损伤可能性的指标之一。2008年，McDannold等[17]发现FUS和微泡诱导兔BBB开放阈值时MI约为0.46。2018年，Tsai等[18]使用FUS联合微泡诱导大鼠BBB开放，发现以MI=1.4的FUS辐照，会使大鼠产生轻微和短期的行为学变化，MI在0.33～0.8时则未引起行为和组织学改变。2020年，Cammalleri等[19]对14项FUS联合微泡诱导BBB开放的动物实验进行综合研究发现BBB开放的最低MI为0.3，而在不引起明显出血或组织损伤的情况下MI为0.7。同时，微泡在BBB开放过程中会产生谐波、表征稳态空化的次/超谐波和表征惯性空化的宽带噪声，采用被动空化检测法监测和量化分析这些参数，也是预测BBB开放程度的一种方法。2012年，O’Reilly等[20]利用FUS联合微泡开放大鼠BBB，基于BBB开放过程中微泡超谐波发射对声压进行放缩以达到实时调制效果，结果表明放缩程度为50%时，BBB成功开放且组织无损伤。2014年，Chen等[21]利用FUS联合微泡作用于小鼠海马体部位BBB，研究分子量为3～2000 kDa药物的递送情况，结果表明当声压增加时BBB可允许更大分子量的药物通过，且不同的空化机理与不同分子量药物的递送有关。2016年，Tsai等[22]利用次谐波能谱密度预测大鼠BBB是否开放，结果表明可有效预测BBB开放。2017年，Sun等[23]提出了基于谐波发射的闭环控制算法，并经健康和荷瘤大鼠实验验证了该算法的有效性。FUS联合微泡已进行了抗体[24]、基因治疗剂[25−27]、化学治疗剂[28]、纳米颗粒[29−30]和细胞[31]等递送的动物实验；近几年，对阿尔兹海默症[32−33]、神经胶质瘤[34]和肌萎缩性侧索硬化症[35]进行了临床试验，探究FUS联合微泡介导BBB开放的安全性、可行性，结果表明该技术增强BBB通透性效果良好且无严重不良反应，关于增强脑部疾病药物治疗的有效性则还需进一步研究。

经颅FUS联合微泡开放BBB临床治疗时，由于人体颅骨个人差异性及其厚度、密度、声衰减系数等非均质性和高声衰减性，需基于患者头颅结构对FUS参数、微泡参数以及安全性、有效性进行进一步探索。本研究利用志愿者人体头颅CT扫描数据、82阵元相控换能器和血管建立三维模型进行经颅数值仿真，研究声学参数、微泡参数诱导BBB开放时对血管靶区MI分布的影响，并在头颅外设置颅内回波信号的接收点，通过定量分析该接收点的检测信号研究靶区微泡的声学特性参数，为临床诱导BBB开放促进治疗药物靶向递送提供理论数据和理论参考。

1 基本方程式及数值仿真模型

1.1 声传播方程

1.1.1 组织中声传播方程

在颅骨和人体脑组织中，采用Westervelt声波非线性传播方程为

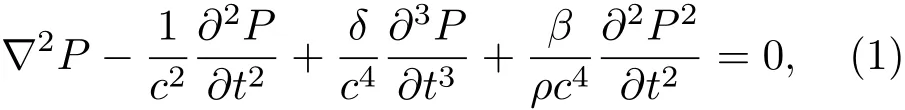
其中，∇2为拉普拉斯算子，P为瞬时声压，c为声波在介质中的传播速度，t为时间，ρ为周围介质密度。声波扩散系数δ=2c3α/ω2，α为介质的衰减系数，角频率ω=2πf，f为频率。声波传播非线性系数β=1+B/(2A)，B/A为介质的非线性系数。

1.1.2 含微泡血液中声传播方程

当微泡的体积分数较低且在流体中分布均匀、初始半径相同时，在流体中的声速恒定的条件下，含微泡流体中的波动方程为[36−37]

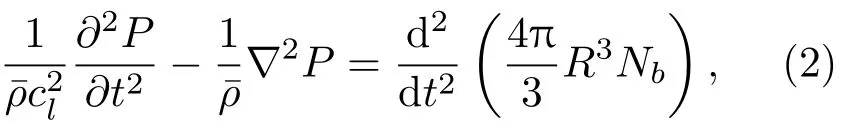
其中，cl为超声波在液体介质中的传播速度，R为微泡瞬态半径。气液混合体的密度¯ρ为

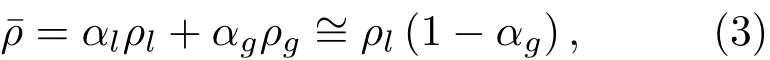
其中，ρl为液体密度，ρg为气体密度，αl为液体体积分数。气体体积分数αg为

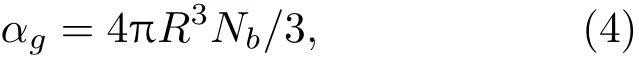
或

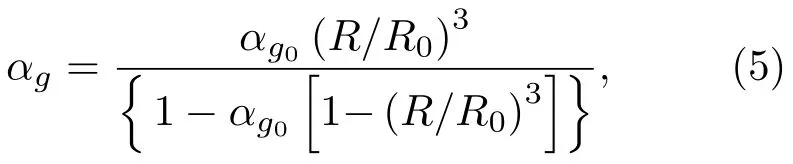
其中，R0为微泡初始半径，αg0为气体初始体积分数。单位体积内微气泡个数Nb为

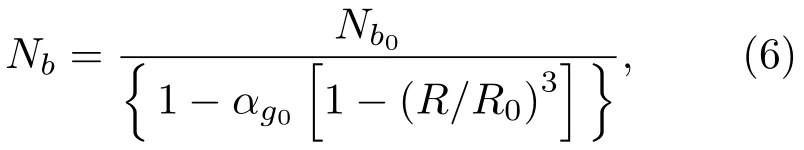
其中，Nb0为微泡初始密度。气液混合物中声波传播方程为

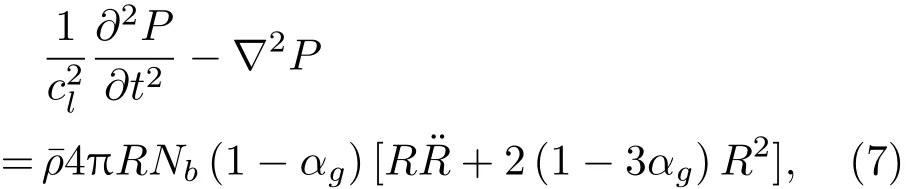
1.2 气泡动力学方程

keller-Miksis方程[38−40]为

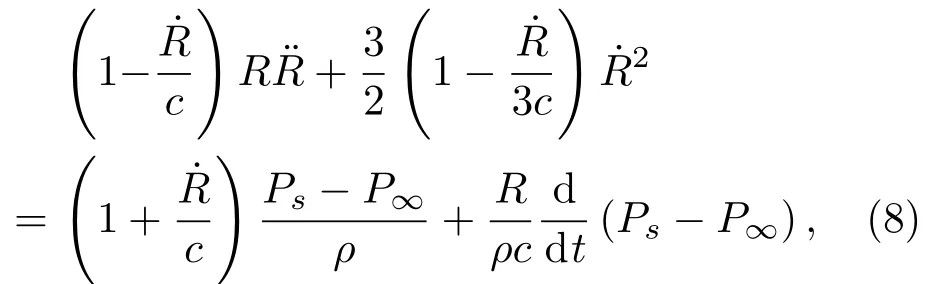
式(8)中，˙R为气泡壁的速度，符号“·”表示一阶导数，Ps为气泡表面处的压强，P∞为无穷远处的压强。Ps−P∞可表示为

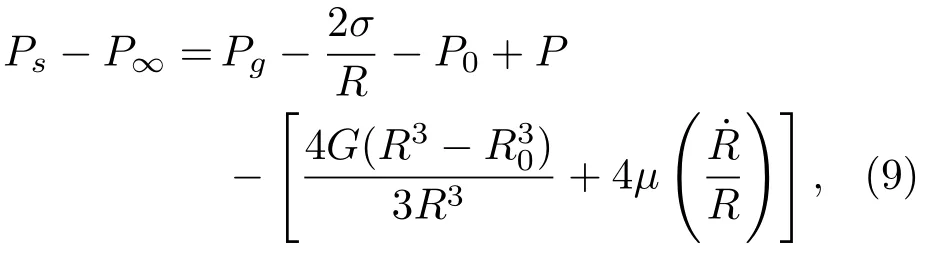
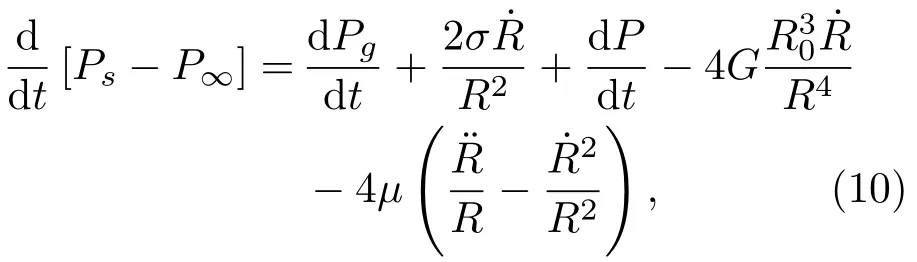
其中，σ为表面张力，G是剪切模量(或刚度)，µ为黏度。气泡内气体压强Pg为

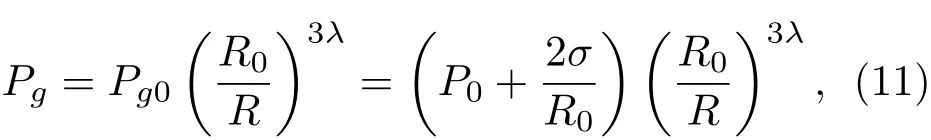
式(11)中，P0是液体静压强，气体多方指数λ=1.4。

1.3 声波参数计算式

机械指数MI为

式(12)中，PPRP表示峰值负压，f为频率。

功率谱密度PSD为

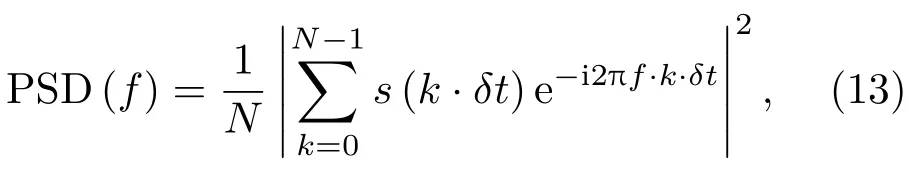
其中，s(k·δt)是脉冲回波接收器接收的声波时域信号，δt为采样时间间隔，k=0,1,2,···,N，N是时域信号序列长度。相对功率谱密度RPSD[41]为

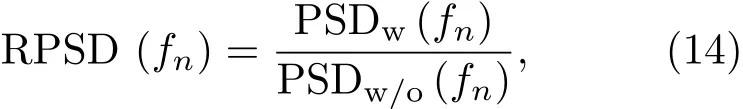
式(14)中，PSDw(fn)为有微泡时功率谱密度，PSDw/o(fn)为相同的超声刺激参数处理下无微泡时的功率谱密度。

次谐波(f/m，m=2,3,4,···)、超谐波(nf/2，n=3,5,7,···)和宽带噪声的发射强度为

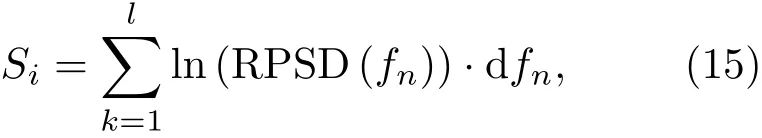
其中，ln表示取自然对数；l为离散信号频谱中各频带覆盖的点数。

1.4 数值仿真模型及参数

图1为由人体头颅CT数据、82阵元相控换能器和血管构成的数值仿真模型。其中人体头颅CT数据(天津医科大学肿瘤医院提供)为62岁女性健康志愿者在120 kV、135 mA、层间隔为3 mm和像素为1 mm条件下的扫描数据；82阵元相控换能器开口直径为100 mm、曲率半径为80 mm；直径d=4 mm的血管放置在换能器的几何焦点处；E1和E2为回波信号接收点，其坐标位置分别为(45.2,0.4,60)、(45.2,119.6,60)。利用时域有限差分(Finite difference time domain,FDTD)法在数值仿真平台上运用CUDA C语言进行仿真计算。数值仿真区域为120 mm×120 mm×120 mm的正方体，空间步长Δx=Δy=Δz=0.4 mm，仿真时间步长Δt=10 ns。

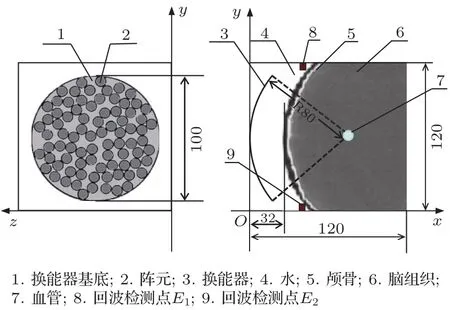
图1 经颅聚焦数值仿真模型图(单位：mm)Fig.1 Numerical simulation model of transcranial focusing(unit:mm)

通过CT图像强度亨氏值H计算颅骨和脑组织的密度ρ、声速c和衰减系数α[42−43]。仿真常数参数[44−46]如表1所示。通过在颅内目标焦点处放置一脉冲点声源信号，数值仿真超声依次穿过脑组织、颅骨、水体到达换能器阵元处的声压信号，经时间反转拟合后可得各阵元处激励信号，对信号利用自相关和互相关法进行处理，可得相位校正和幅度调控后的阵元激励信号[43]。

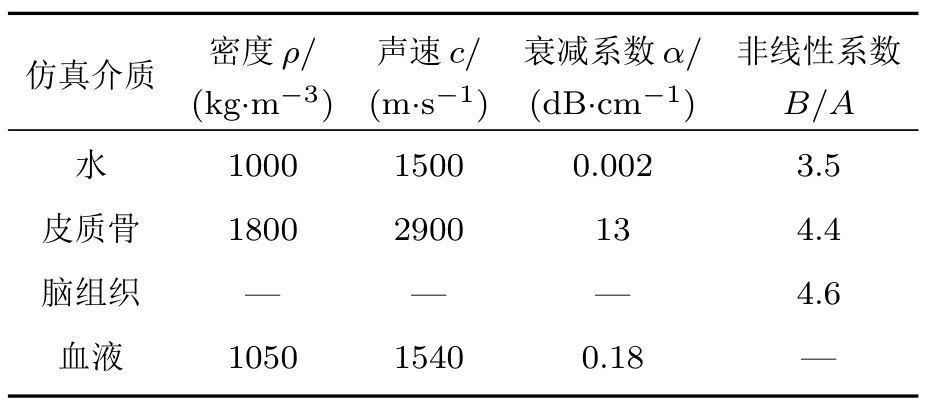
表1 数值仿真参数Table 1 Numerical simulation parameters

2 结果

在辐照时间为1 s、脉冲重复频率为1 Hz、占空比为0.04%的条件下进行如下数值仿真研究。

2.1 微泡的影响

在超声输入功率0.7 W、频率0.7 MHz、微泡初始半径6µm和微泡的初始密度Nb0分别为0和1.56×1010/m3的条件下，聚焦形成的焦域声压分布如图2所示。其中，图2(a)、图2(b)分别为无微泡(Nb0=0)和有微泡(Nb0=1.56×1010/m3)条件下焦域的峰值声压分布图，白色圆圈表示血管；图2(c)为与图2(a)、图2(b)对应声轴上的声压曲线图，蓝色实线为无微泡时声轴声压曲线，红色实线为Nb0=1.56×1010/m3时声轴声压曲线；图2(d)为焦点处声压信号的功率谱密度曲线图。由图2可知，当血管中有微泡时，血管内形成高声压区，焦点声压升高，形成0.35 MHz的次谐波和1.05 MHz的超谐波。

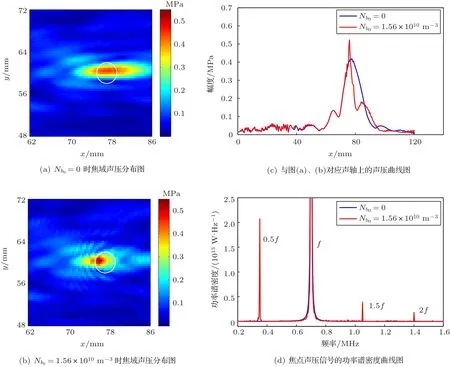
图2 焦域声压分布图Fig.2 Distribution of sound pressure in focal region

2.2 声功率的影响

当超声频率为0.7 MHz、微泡初始半径为6µm和微泡的初始密度Nb0为1.56×1010/m3时，不同声功率下形成的焦域MI分布如图3所示。其中，BBB可安全有效打开0.3≤MI≤0.7的区域用绿色表示，可能会造成血管或脑组织损伤MI>0.7的区域用红色表示，BBB未能有效打开MI<0.3的区域用蓝色表示。图4为与图3对应不同声功率条件下形成焦点处峰值负压与MI值随声功率变化曲线图，其中图4(a)为峰值负压随声功率变化曲线图，图4(b)为MI最大值MImax和MI>0.3区域的面积随声功率变化曲线图。由图3、图4可知，随着声功率的增大，0.3≤MI≤0.7绿色区域面积、焦点处的峰值负压、MImax和MI>0.3的区域面积均增大；当声功率增加到1 W时，出现了MI数值高于0.7的红色区域，且随着声功率继续增加，红色区域面积也增大。

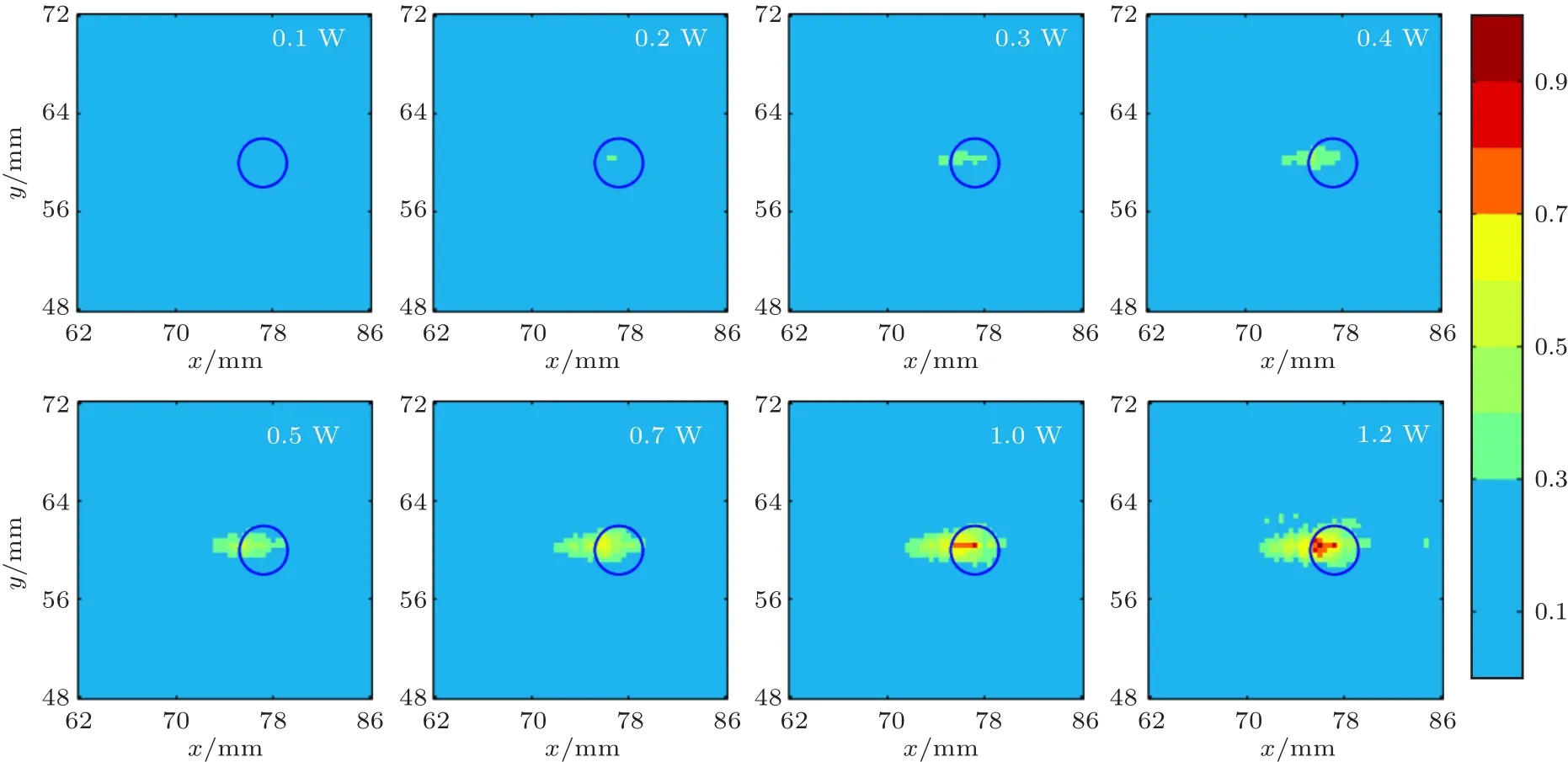
图3 不同声功率下焦域MI分布图(蓝色圆圈为血管)Fig.3 MI distribution in focal region at different acoustic power(The blue circle is blood vessel)

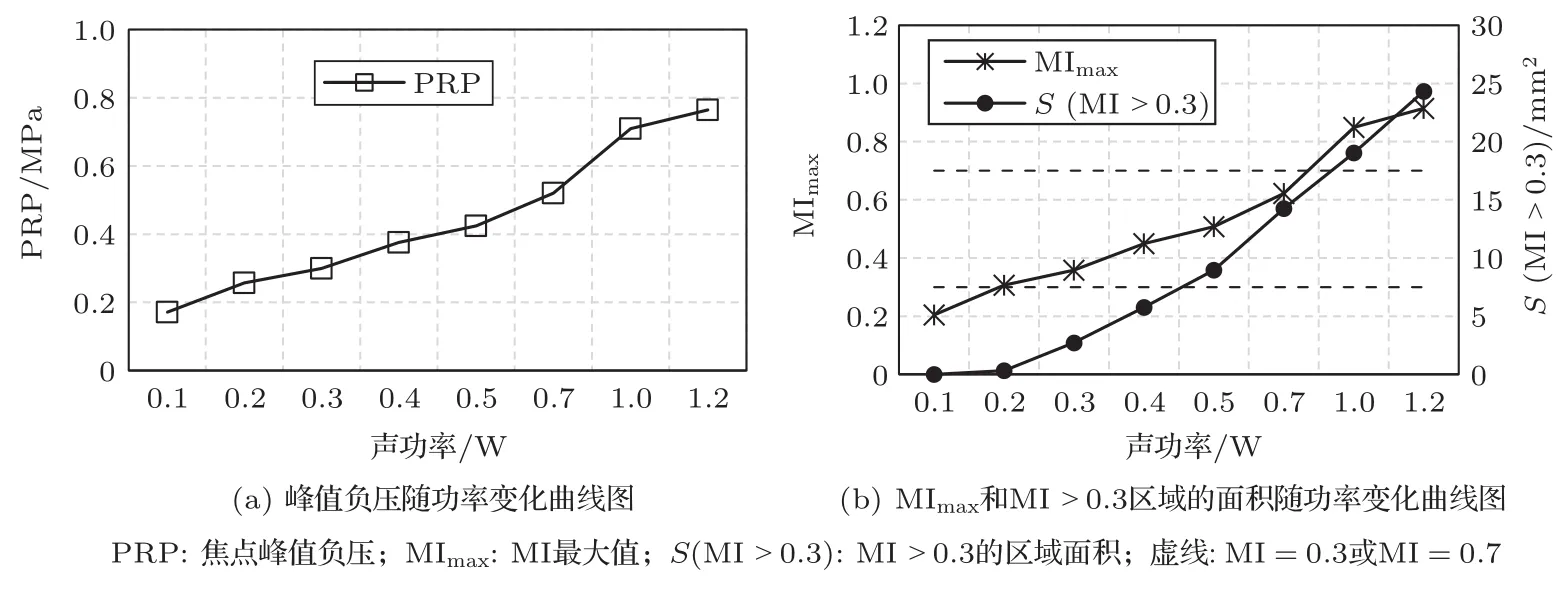
图4 焦点峰值负压与MI值随声功率变化曲线图Fig.4 Curve of peak rarefactional pressure and MI value at the focus with acoustic power

图5为与图3对应条件下，在E1和E2点处随声功率变化的声发射强度曲线图。其中图5(a)为声功率为0.5 W时E1处取对数后相对功率谱密度图，图5(b)、图5(c)分别为次谐波(f/2±10 kHz)、超谐波(3f/2±10kHz)和宽带噪声(2f+80kHz～2.5f−80kHz)强度曲线图。由图5(b)、图5(c)可知，随声功率的增加，次谐波强度先增大后减小再增大，超谐波强度先增大再减小，宽带噪声强度一直增大；当声功率0.5 W时，次谐波、超谐波强度值较大，说明此时稳态空化强度较大，为此，下文选用0.5 W的声功率条件进行仿真研究。

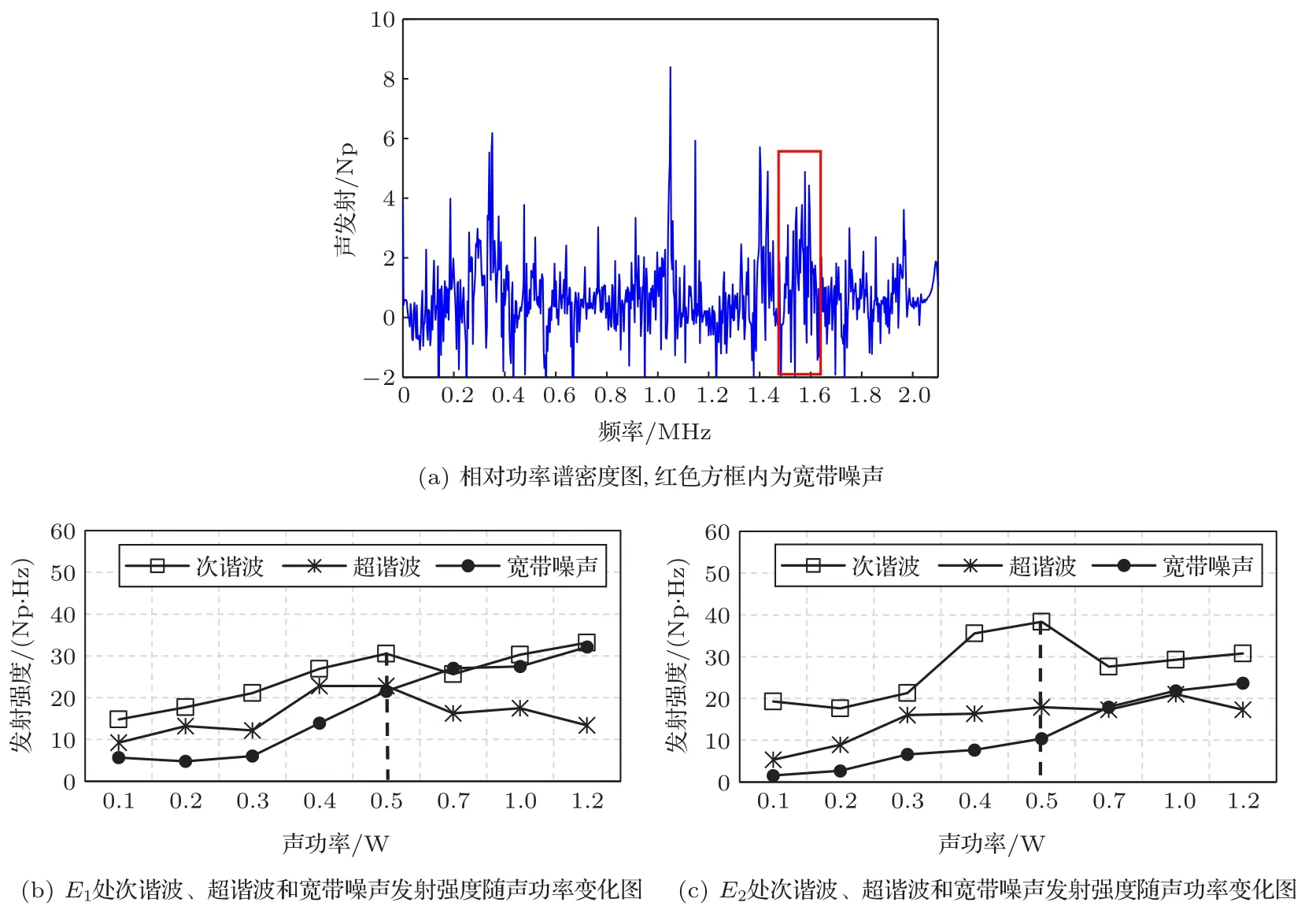
图5 声发射强度随声功率变化曲线图Fig.5 Curve of acoustic emission strength with acoustic power

2.3 频率的影响

当声功率为0.5 W、微泡初始半径为6µm和微泡初始密度Nb0为1.56×1010/m3时，不同超声频率下形成的焦域MI分布如图6所示。图7为与图6对应不同频率条件下形成焦点处峰值负压、MI值随频率变化的曲线图。其中图7(a)为峰值负压随频率变化曲线图，图7(b)为MI最大值MImax和MI>0.3区域的面积随频率变化曲线图。由图6、图7可知，随着频率的增加，0.3≤MI≤0.7绿色区域、MI>0.3区域的面积均减小；随着超声频率的增大，焦点峰值负压和MImax先增大再减小，超声频率为0.5 MHz时MImax最大；未出现MI>0.7的红色区域。

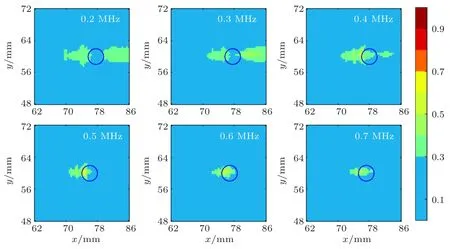
图6 不同频率下焦域MI分布图(蓝色圆圈为血管)Fig.6 MI distribution in focal region at different frequency(The blue circle is blood vessel)

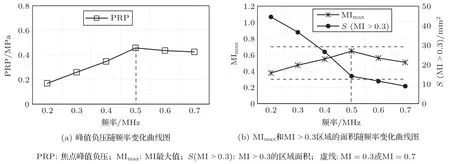
图7 焦点峰值负压与MI值随频率变化曲线图Fig.7 Curve of peak rarefactional pressure and MI value at the focus with frequency

图8为与图6对应条件下，在E1与E2点处随频率变化的声发射强度曲线图。图8(a)、图8(b)分别是E1和E2处次谐波、超谐波及宽带噪声强度曲线图。由图8可知，随频率的增大，次谐波和超谐波强度逐渐增大，宽带噪声发射强度无明显规律。基于0.5 MHz时MImax最大，下文将在0.5 MHz的超声频率条件下进行仿真研究。

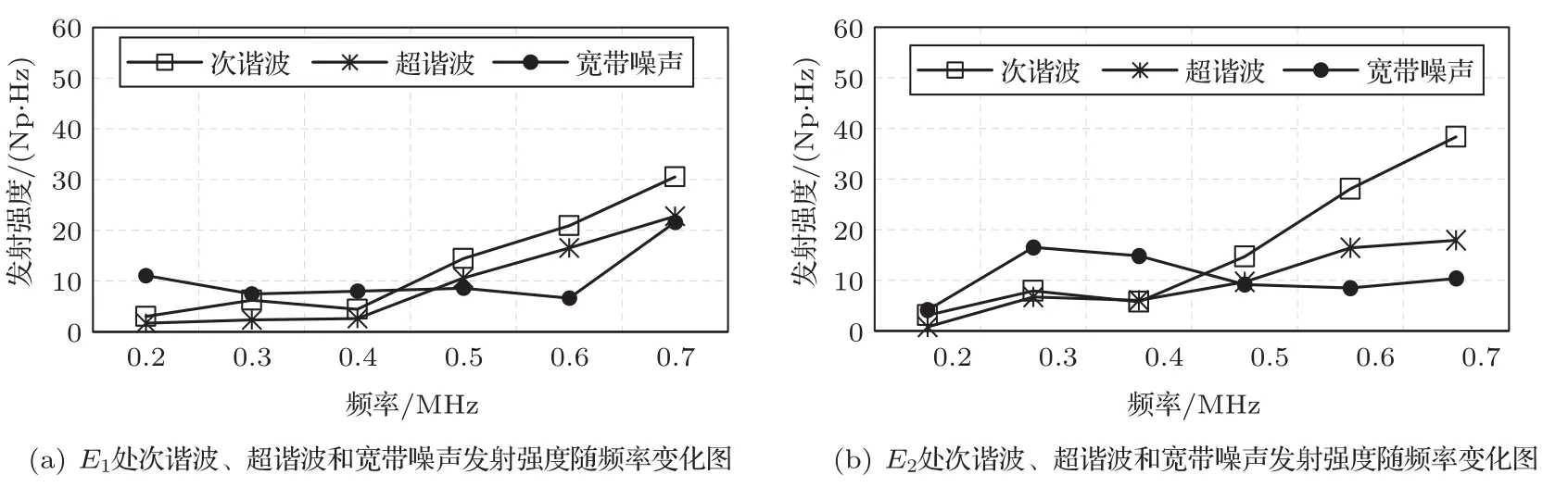
图8 声发射强度随频率变化曲线图Fig.8 Curve of acoustic emission strength with frequency

2.4 微泡初始半径的影响

当声功率为0.5 W、频率为0.5 MHz和微泡初始密度Nb0为1.56×1010/m3时，微泡初始半径为1～10µm时形成的焦域MI分布如图9所示。图10为与图9对应不同微泡初始半径条件下形成焦点处峰值负压和MI值随微泡初始半径变化曲线图，其中，图10(a)为峰值负压随微泡初始半径变化曲线图，图10(b)为MImax和MI>0.3区域的面积随初始半径变化曲线图。由图9、图10可知，随着微泡初始半径的增大，0.3≤MI≤0.7绿色区域的面积和MI>0.3区域的面积均先减小后保持不变；未出现MI>0.7的红色区域；在微泡初始半径为1～10µm范围内，随微泡初始半径增大焦点峰值负压和MImax产生波动，呈现先增大后几乎保持不变趋势，微泡初始半径为6µm时，焦点峰值负压和MImax最大。

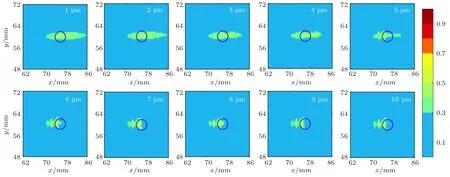
图9 不同微泡初始半径下焦域MI分布图(蓝色圆圈为血管)Fig.9 MI distribution in focal region at different initial radii of microbubbles(The blue circle is blood vessel)

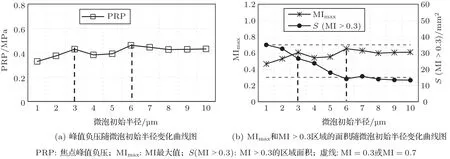
图10 焦点峰值负压和MI值随微泡初始半径变化曲线图Fig.10 Curve of peak rarefactional pressure and MI value at the focus with initial radii of microbubbles

图11为与图9对应条件下，在点E1与E2处随微泡初始半径变化的声发射强度曲线图。图11(a)、图11(b)是E1和E2处次谐波、超谐波及宽带噪声强度曲线图。由图11可知，当微泡初始半径为1～5µm时，次谐波、超谐波及宽带噪声的强度基本不变。当微泡初始半径大于5µm时，次谐波和超谐波发射强度显著增大，宽带噪声基本保持稳定。

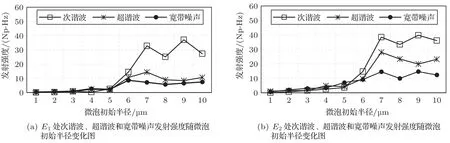
图11 声发射强度随微泡初始半径变化曲线图Fig.11 Curve of acoustic emission strength with initial radii of microbubbles

2.5 微泡初始密度的影响

当声功率为0.5 W、超声频率为0.5 MHz和微泡初始半径为6µm时，不同微泡初始密度Nb0形成的焦域MI分布如图12所示。图13为与图12对应不同微泡初始密度条件下形成焦点处峰值负压和MI值随微泡初始密度变化曲线图，其中，图13(a)为峰值负压随微泡初始密度变化曲线图，图13(b)为MImax和MI>0.3区域的面积随微泡初始密度变化曲线图。由图12可知，随着微泡初始密度的增加，0.3≤MI≤0.7绿色区域的面积逐渐减小，血管内绿色区域也在减小。当微泡初始密度为2.39×1010/m3时，出现了MI>0.7的红色区域。由图13可知，随着微泡初始密度的增大，焦点峰值负压和MImax逐渐增大，而MI>0.3区域的面积随着微泡初始密度增大先减小后保持不变。

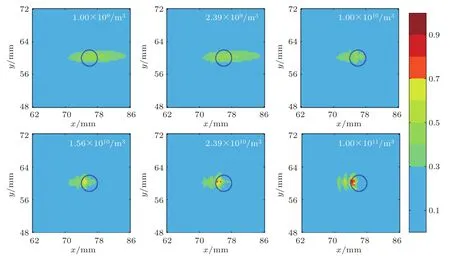
图12 不同微泡初始密度下焦域MI分布图(蓝色圆圈为血管)Fig.12 MI distribution in focal region at different initial density of microbubbles(The blue circle is blood vessel)

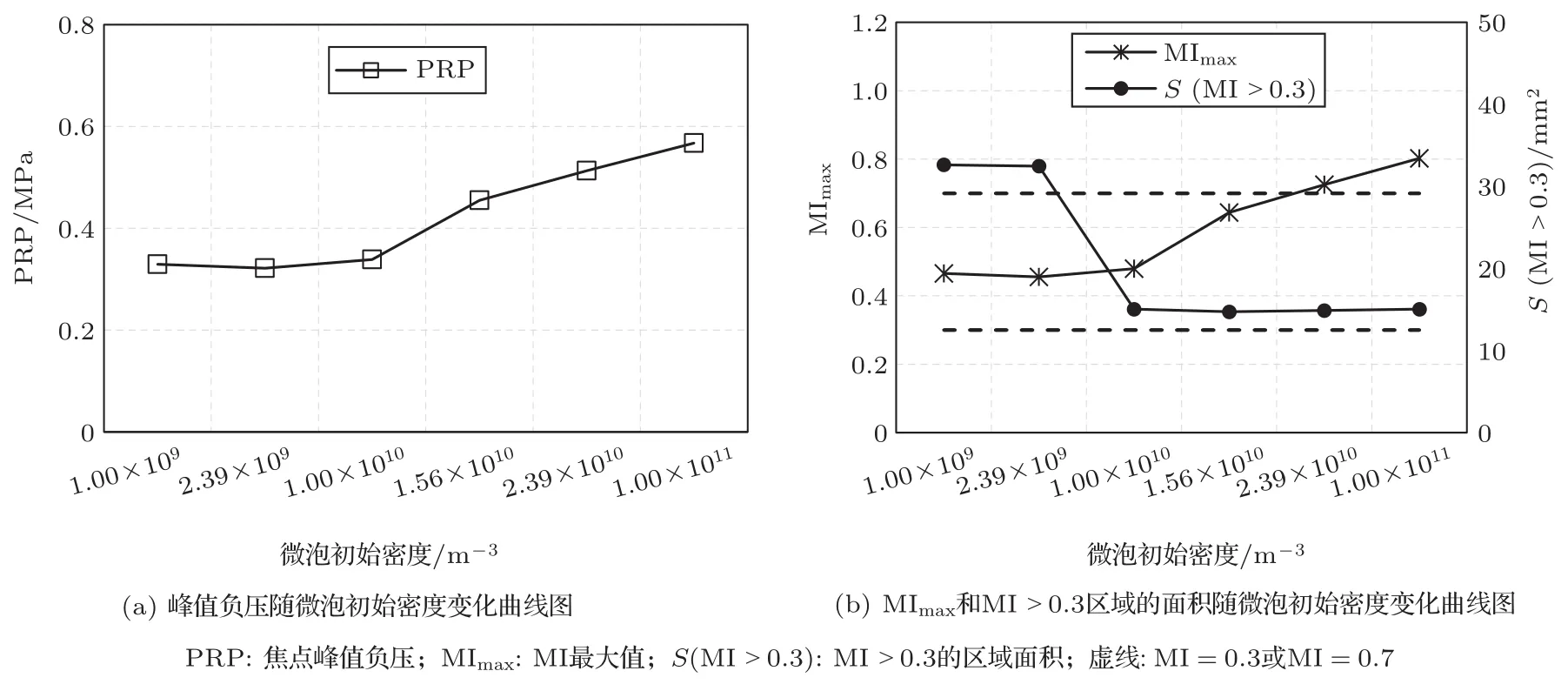
图13 焦点峰值负压和MI值对微泡初始密度变化曲线图Fig.13 Curve of peak rarefactional pressure and MI value at the focus with initial density of microbubbles

图14为与图12对应条件下，在点E1与E2处随微泡初始密度变化的声发射强度曲线图。图14(a)、图14(b)是E1和E2处次谐波、超谐波及宽带噪声强度曲线图。由图14可知，随着微泡初始密度的增大，观察到次谐波、超谐波及宽带噪声强度逐渐增大。

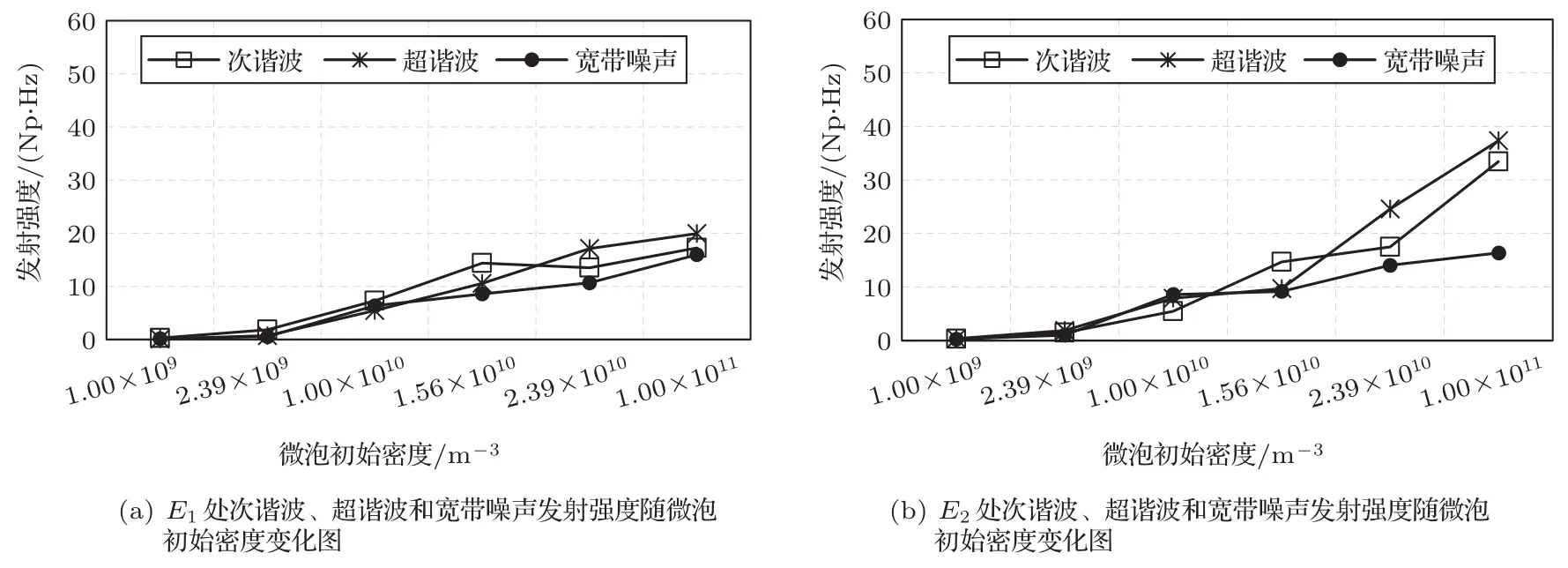
图14 声发射强度随微泡初始密度变化曲线图Fig.14 Curve of acoustic emission strength with initial density of microbubbles

3 讨论

在实际临床治疗中需要考虑组织热损伤问题，在这里以超声频率0.7 MHz、输入功率1.2 W、辐照时间60 s、微泡初始半径6µm和初始密度为1.56×1010/m3为例，利用Pennes生物热传导方程[47]：

其中，单位体积发热量q=2αI，I为声强；在水、脑和皮质骨的比热Cr分别为4180 J·kg−1·K、1840 J·kg−1·K和3700 J·kg−1·K，热传导率rec分别为0.6 W·m−1·K、1.3 W·m−1·K和0.465 W·m−1·K，其他参数与表1相同的条件下，忽略血流灌注(WB=0.0)后数值仿真获得焦点处最高组织温升T=2.77°C[48]，不会引起脑组织热损伤。由于FUS经颅传播时受颅骨结构和特性影响，为降低声压衰减和相差影响，使用较低频率FUS联合微泡促进BBB开放，适宜的频率范围为0.2～0.7 MHz[19]，本文也在该频率范围内进行了分析，并发现在初始半径为6µm条件下频率为0.5 MHz时MImax最大。本文研究结果表明超声的频率影响焦域的形状和大小，频率越高产生的焦域越小，BBB有效开放的面积减小(图6)，这与2018年Shin等[13]的研究结果一致。本文宽带噪声计算频带参考了文献[41]和文献[49]，当微泡初始半径和微泡密度越大时，次谐波、超谐波和宽带噪声强度越大，可能导致更大的BBB开口或组织损伤(图11和图14)，该结果与Yang和Choi等的研究结果[50−52]相一致；当微泡初始半径为3µm和6µm时焦点处MImax出现了波动(图10)，超声频率约为共振频率的半倍频或接近共振频率，考虑是驱动共振响应的结果，但具体机制还需进一步验证；位处于声轴对称位置的点E1和E2处接收的回波信号强度有差异(图5、图8、图11和图14)，该差异时由颅骨非均质声学特性结构引发的。本研究仅用一名志愿者头颅CT数据和单一血管建立三维模型进行了数值仿真，人体的个体差异性未能考虑，下一步可采用多个志愿者头颅CT数据进行统计分析超声参数与微泡参数的影响；本研究中仅考虑FUS功率和频率对BBB开放的影响，如脉冲持续时间和总辐照时间等也会影响BBB开放程度，有待进一步研究。

4 结论

本文基于人体头颅CT、82阵元相控超声换能器和血管建立了经颅数值仿真模型，对超声辐照下颅内的声压传播进行研究，并依据被动空化检测法在颅外设置接收点记录目标位置处微泡的振荡情况，比较在不同的超声参数和微泡参数下MI分布和声发射强度的变化，从定性和定量的角度分析不同的参数选择对声压场、MI分布及靶区声发射强度的影响。上述数值仿真的结果如下：

(1)当血管中有微泡时，血管内会形成高声压区，有次谐波和超谐波形成。

(2)随声功率和微泡初始密度的增大，焦点峰值负压和MImax增大，当声功率和初始密度较大时，可能出现MI大于0.7引发脑组织损伤；随频率的增大，焦点峰值负压和MImax先增大再减小，随微泡初始半径增大焦点峰值负压和MImax呈现先增大后保持不变趋势。

(3)随声功率的增大MI>0.3的区域面积增大，随频率和微泡初始密度的增大MI>0.3的区域面积减小，而随着微泡初始半径的增大MI>0.3的区域面积先减小后几乎保持不变，在微泡初始半径为6µm时，MImax最大。

(4)当声功率为0.5 W时，次谐波、超谐波强度较大；次谐波和超谐波的强度随频率和微泡初始密度增大而增大，当微泡初始半径为1～5µm时，次谐波和超谐波维持在较低水平，当初始半径大于5µm时，次谐波和超谐波强度显著增加。

(5)随声功率和微泡初始密度的增大，宽带噪声强度增大，超声频率和微泡初始半径的变化对宽带噪声的影响无明显规律。

基于上述结果可得到如下结论：

(1)微泡可使超声能量集聚，形成次谐波和超谐波。

(2)随着声功率和微泡密度的增大，焦点处MI和宽带噪声强度增大，当声功率过大和微泡密度过高时，可能损伤靶区组织。

(3)超声频率的增大会使次谐波和超谐波强度增大，微泡半径较小时，空化强度维持在较低水平，当微泡半径大于5µm时，次谐波和超谐波强度显著增大。

致谢感谢天津医科大学肿瘤医院提供的志愿者头颅CT扫描数据。