传声器次声段灵敏度校准的误差机理研究∗

刘 迪 刘爱冰 陈 峰 张 帆王慧恒 武际兴

(1 山东理工大学交通与车辆工程学院 淄博 255000)

(2 杭州新声传感科技有限公司 杭州 310000)

0 引言

次声波广泛存在于自然界与人类的各种活动中，次声声压的准确测量是人体避免次声伤害和次声技术广泛应用的关键。次声波的定量研究依托传声器的精确测量实现。由于传声器受泄漏和热传导因素影响，具有明显的低频非线性衰减特征，因此揭示次声传声器校准过程中多物理因素综合作用下传声器的灵敏度变化误差机理是保证传声器精确测量，也是声压量值溯源的根基。

传声器的声学校准分为次级校准和原级校准。次级校准是使用比较法对传声器进行校准[1]，其校准精度取决于比较中更高等级的参考传声器，而参考传声器的灵敏度是经过原级校准得到的。原级校准方法是通过参照非声学标准进行校准，能够达到尽可能高的精度。原级校准方法主要包括耦合腔互易法和活塞发生器法[2−3]，但耦合腔互易法的声阻抗模型不适用次声段校准，而活塞发生器法能够作为互易法的补充来进行次声段的校准。活塞发生器产生的标准压力信号与活塞位移、腔体结构参数等直接相关，并有相应的修正理论对其误差因素进行补偿，可保证次声声压量值溯源到国际单位。活塞发生器法依据激励源不同包含扬声器激励[4]、激振器激励[5]、标准振动台激励[6]和电机激励[3]等多种形式，前三者均不能输出恒定幅相频特性的激励，造成传感器校准的不便。此外，扬声器、激振器激励在低频段位移输出的信噪比很差，而标准振动台的调试和维持精度较为困难，并需要激光测振仪等实现反馈，成本十分高昂，不便推广。而目前市场上的商用化伺服电机能够覆盖0.01～100 Hz的校准频率，因此以伺服电机为激励源的活塞发生器能够满足传声器在次声段的原级校准。

国内外学者对次声段校准核心泄漏、热传导等因素对传声器灵敏度响应的影响进行了一些研究。Frederiksen[7]采用电声类比方法构建出了考虑传声器后腔的泄漏和热传导效应低频灵敏度模型，得出了传声器分别在校准腔内的声场和外界大气声场中灵敏度频率响应，但是由于模型中的大量参数没有确定物理含义，使得该方法只适用于定性研究。裘剑敏等[8]指出传声器的频率响应受到其均压孔所处位置的影响，发现由于均压孔的位置不同，传声器后腔声顺随频率降低而变化，从而造成灵敏度校准偏差。Marston[9]设计了适应于0.002～20 Hz频率范围内校准的次声活塞发生器，通过阻抗类比法建立了考虑黏滞损耗的校准声压模型，发现传声器的相位灵敏度在低频段会出现相位超前的现象。张炳毅等[10]指出泄漏和热传导等因素是制约校准低频截止频率的主要原因，也是影响低频校准关键。以上方法虽然发现了泄漏与热传导效应在校准过程对传声器响应的影响，但均没有定量研究校准结果中的误差机理。

传声器的幅值校准是实现次声声压量值的复现和传递的关键。而传声器的相位校准是保证次声声源信号定位精度的核心[11−12]。目前中国科学院声学研究所已在全国建立多个次声监测站点，用于检测和确定在次声范围内的声源定位，为我国的环境次声监测提供了数据支撑。研究传声器灵敏度幅值与相位校准中因多物理效应作用而产生的误差机理是次声防护和应用的技术保障。

1 压力泄漏与热传导的幅相特性

1.1 原级校准下的双重耦合机制

基于低速伺服电机激励的活塞发生装置能够实现低频测量下限达到0.01 Hz[7]，如图1所示。校准装置的工作原理是伺服电机推动活塞在校准腔体内做往复运动产生声压，依据理想气体状态方程确定活塞发生装置腔内的校准声压。

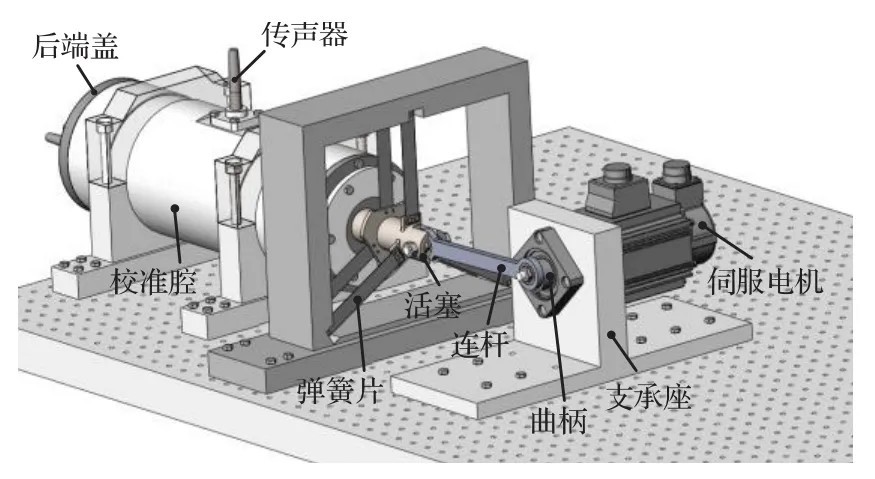
图1 活塞发生装置原级校准平台Fig.1 Primary calibration platform of pistonphone

活塞发生装置在次声段对传声器进行校准时，活塞发生装置校准腔和传声器后腔均因压力泄漏和热传导耦合作用(第一重耦合机制)产生声压衰减[8]。传声器振膜两侧的声压耦合作用(第二重耦合机制)改变了振膜的变形量，造成了传声器输出电压的变化，进而改变传声器灵敏度的频率响应。校准过程中多物理因素综合作用构成了被校传声器原级校准的双重耦合机制，如图2所示。

图2 传声器原级校准的双重耦合机制示意图Fig.2 Dual-coupling mechanism in the primary pistonphone calibration

1.2 压力泄漏与热传导损失的理论分析

活塞发生装置对传声器进行灵敏度校准时，校准声压的衰减是校准误差的引入因素，而传声器的后腔声压衰减是灵敏度特征的构成因素。研究校准腔与后腔内声压泄漏与热传导损失的响应是提高传声器灵敏度校准精度的前提。

在次声段进行校准时，压力泄漏和热传导效应的耦合作用会造成校准腔和传声器后腔内的声压衰减。为了准确揭示次声段下泄漏与热传导效应的耦合机制，Zhang等[13]基于模型等效思想以及准静态假设建立校准声压的泄漏和热传导耦合衰减模型：

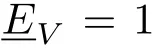
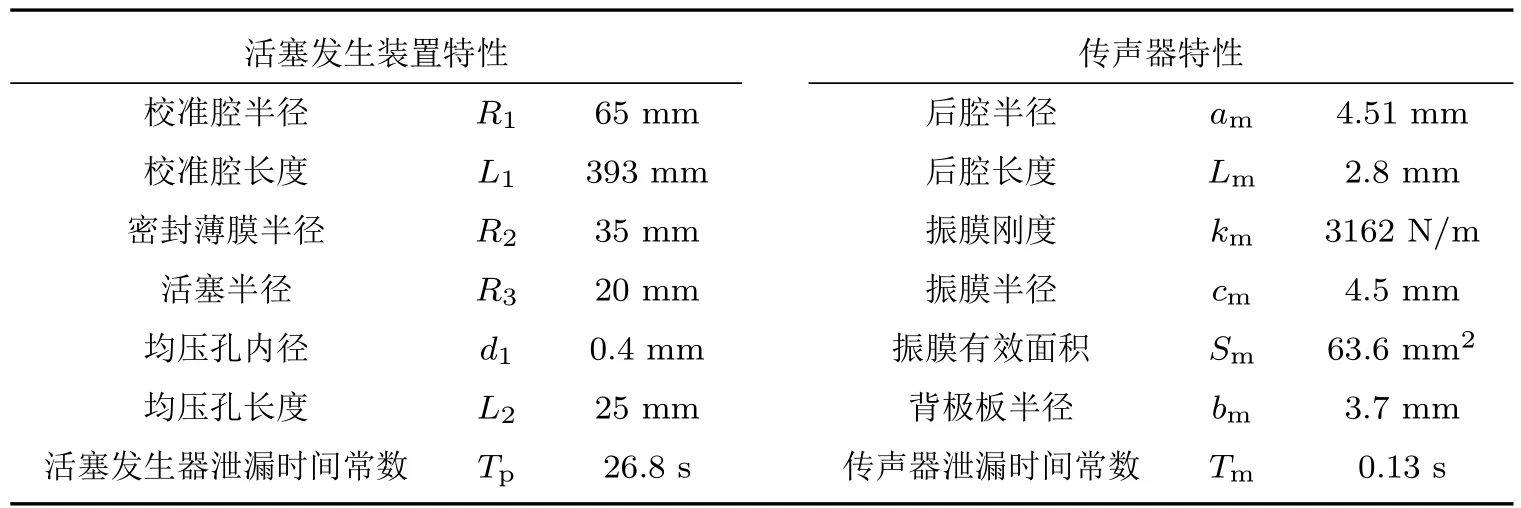
表1 活塞发生装置和传声器的特性参数Table 1 Characteristic parameters of pistonphone and microphone

表1中的传声器是精密仪器，其结构参数难以精确测量，表中的传声器结构参照了CHZ-213传声器的声腔模型，传声器的性能参数是通过参考一系列传声器的结构尺寸估算得出。目前市场上普通传声器的下限截止频率为1 Hz左右，有少数次声传声器(如BK-4193和PCB-378A07)的下限截止频率达到0.1 Hz左右。但对于大多数的声学校准而言，对下限工作频率为1 Hz左右的传声器配合特殊的低频前置放大器(如PCB-426E01，下限截止频率小于0.9 Hz)与低频信号调理器(如PCB-480C02，工作频率为0.05～500 kHz)进行内外均压校准，能够揭示内外均压校准模式下灵敏度的波动规律(第3节的校准实验部分进行了详细的说明)，因此本文选择了下限截止频率为1 Hz左右的传声器进行分析。通过第1.3节对考虑泄漏效应造成的传声器后腔声压损失进行理论和仿真对比验证(如图5(a)所示)，得出传声器的下限截止频率为1.25 Hz。并结合Rennie给出的泄漏修正表达式[14]：

式(2)中，plc为泄漏修正量。将传声器的下限截止频率125 Hz代入式(2)，得出传声器的泄漏时间常数为0.13 s。算得理论泄漏时间常数比实际泄漏时间常数略大，但不会影响传声器的幅相频响应趋势。

1.3 压力泄漏与热传导损失的仿真分析

为了验证压力泄漏和热传导耦合衰减模型的可靠性，根据活塞发生装置与传声器的有效腔体，在COMSOL Multiphysics软件的热黏滞声学模块中等效构建考虑泄漏通道热黏滞损耗的流场边界和考虑腔壁温度分布的温度场边界下的密封腔与泄漏腔模型。对传声器建模时，为了提高计算效率，利用模型的对称性建立传声器的1/12有限元模型以简化计算域。校准腔与传声器有限元模型的材料均设置为空气。

为了真实模拟校准腔内声压变化规律，在活塞表面施加轴向的等效速度边界v=2πf×5[mm]。受黏滞作用影响，设定活塞激励面以外腔壁的速度边界为0。对于考虑热传导效应的两个模型，将校准腔壁设置为等温壁。两个绝热模型的校准腔壁设置为绝热壁。对于考虑压力泄漏效应的两个模型，设置均压孔外端始终与外界大气连通，而密封模型设置为外端封闭。在腔壁上添加了5层边界层网格，并沿着无滑动边界剖分边界层网格以提高网格解析度与收敛性。

在校准腔中部安装传声器的位置处添加域点探针，基于速度激励边界，在0.1 Hz下对热传导-密封、绝热-泄漏、热传导-泄漏与绝热-密封4个校准腔的有限元模型分别进行数值模拟，确定不同工况下校准声场的分布如图3所示。

为了准确量化校准腔内声压在次声段的泄漏与热传导损失，提出了模型比较法，通过将绝热-密封工况下校准声压的幅值与相位响应分别与热传导-密封、绝热-泄漏以及热传导-泄漏工况下声压的响应相减确定出各修正量(以0.1 Hz处的声压分布为例)如图3所示。

图3 基于模型比较法量化各修正量的示意图Fig.3 Schematic diagram of quantifying each correction based on model comparison method

同样地，对传声器的振膜面添加等效的轴向速度边界v=2πf×0.5[µm]。其余边界条件均与活塞发生装置校准声场的边界设置一致。传声器泄漏腔和密封腔模型在1 Hz下声压分布云图如图4所示。

根据图4可以看出，热传导-密封工况下的后腔声压在1 Hz时的衰减量已经达到3 dB，两种泄漏工况下的后腔声压衰减量明显大于热传导工况。

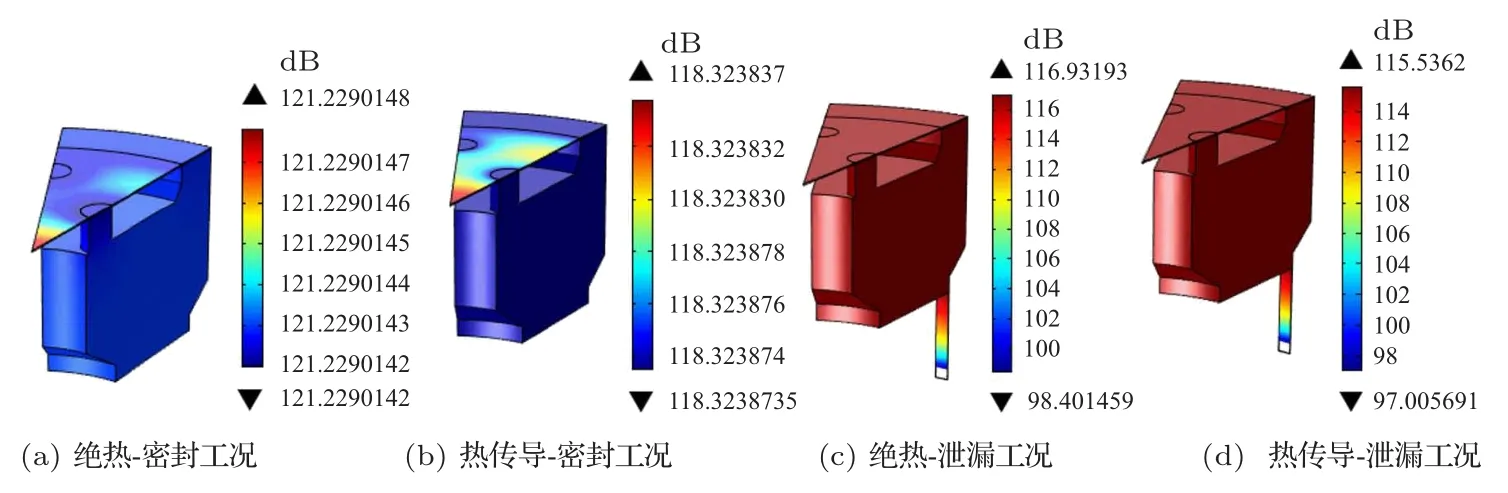
图4 不同工况的后腔声压在1 Hz下的声场分布Fig.4 Sound field distribution of back-chamber sound pressure at 1 Hz under different conditions

为准确量化次声段校准核心的泄漏、热传导独立修正量与耦合修正量，并揭示各修正量的幅相特性变化规律，对活塞发生装置与传声器在频域模块下进行独立数值模拟时，设置频率范围为0.1 mHz～100 Hz，频率间隔为1/3倍频程。校准腔与后腔内声压泄漏与热传导损失的理论值与仿真值对比结果如图5所示。

从图5可以看出，不同腔内声压泄漏与热传导损失的幅值与相位响应是同时产生的。热传导损失的幅值为3 dB，并在中低频段产生较小的相位偏差。而泄漏损失的幅值远大于热传导，在极低频率下声压的泄漏损失会产生90°的相位超前。当校准腔内耦合损失的幅值为3 dB时，伴随产生了33°左右的相位超前，对应校准腔的下限截止频率为0.01 Hz。

在实际校准时，由于较小的腔体会产生更大的压力泄漏和热传导损失，因而传声器后腔声压的衰减比校准声压的衰减提前。根据第二重耦合机制(压力耦合)，可以推测出传声器的振膜在次声段会产生变形，从而引起传声器次声段灵敏度的变化。

基于仿真模型比较法确定出校准声压泄漏与热传导的独立与耦合修正量。通过将各修正量的仿真值与式(1)算得的理论修正量进行对比，验证并揭示修正误差机理如表2所示。进一步将校准声压泄漏和热传导独立修正总量与耦合修正量的幅值响应进行对比，次声段下两种修正量幅值的理论响应与仿真响应对比误差如表2所示，从而定量评判热黏滞损耗、腔壁不等温和均压孔泄漏等因素对声压变化的影响。

表2 校准声压泄漏与热传导效应的独立与耦合修正误差对比Table 2 Comparison of independent and coupling correction errors of calibration pressure leakage and heat conduction

根据表2可以看出，校准声压泄漏损失的幅值与相位响应在理论与仿真结果中存在微小差异，主要是仿真模型中的均压孔与活塞发生装置实际加工均压孔的尺寸之间存在偏差引起的。热传导损失的幅值与相位响应在理论与仿真结果中分别存在0.12 dB和0.58°以下的微小差别，主要是有两方面原因，一方面是源于理论模型没有计算黏滞损失，另一方面是由于理论模型采用等直圆柱体，其与设计的腔体前端薄膜密封结构略有差别。

在表2中发现，泄漏与热传导耦合损失的幅值为3 dB(对应频率0.01 Hz)之前的高频偏差在0.1 dB左右，不会对衰减规律产生明显的影响。在低于0.01 Hz范围内，校准腔内泄漏与热传导效应的独立修正总量与耦合修正量在次声段存在明显差异，主要是由于泄漏与热传导效应相互耦合，泄漏损失的衰减使得热传导减慢，反之亦然，进而验证了数值模拟结果与理论解析结果的一致性。

2 传声器灵敏度的联合仿真

校准传声器的关键是校准声压激励传声器的振膜。但传声器与活塞发生装置的体积相差甚大，同时考虑到仅校准声场对传声器输出有明显的影响。为提高运算效率和精度，对活塞发生装置和传声器分别进行数值模拟，将活塞发生装置的校准声压施加在传声器振膜上，实现传声器灵敏度校准的联合仿真。

应用COMSOL Multiphysics中的热黏滞声学模块、结构场(膜模块)与静电场模块3个物理场进行耦合。设置振膜的材料、厚度以及膜的初始预应力，在振膜的外边缘添加固定约束。此外，在振膜与后腔之间设置热黏滞声学和固体结构力学耦合边界实现振膜与声场的耦合，校准声压与静电力分别施加在振膜上，真实模拟对传声器灵敏度的内外均压原级校准。内均压校准是指传声器的均压孔置于活塞发生器的校准腔内部，保证传声器的均压孔与校准声场连通。外均压校准是指传声器的均压孔置于校准声场外部，即均压孔与外界大气连通，内外均压校准机制如图6所示。

图6 内外均压校准机制Fig.6 The mechanism of calibration for vent in field and vent out field

2.1 传声器振膜变形的幅相频响应

为揭示多物理效应在灵敏度校准过程中的误差机理，将绝热-密封、绝热-泄漏、热传导-密封、热传导-泄漏4种工况下校准腔的有限元模型与传声器在热传导-泄漏工况下的有限元模型分别进行多物理场联合仿真，进而分析活塞发生装置特性对传声器灵敏度幅相特性变化规律的影响，传声器振膜变形幅值与相位响应的仿真结果如图7所示。

从图7(a)可以看出，内外均压校准声场中的传声器振膜变形存在很大差异，尤其在10 Hz以下，外均压校准声场中的振膜变形量总是大于内均压校准声场中的变形量。当均压孔置于校准声场时，随着频率的降低，传声器振膜的变形因作用在其两侧声压压差的减小而减小。对于外均压校准，振膜变形由活塞发生装置的校准声压决定，而校准腔在次声段的压力泄漏和热传导效应明显。因而不同工况下校准声压的激励造成了传声器振膜变形频率响应的不同。

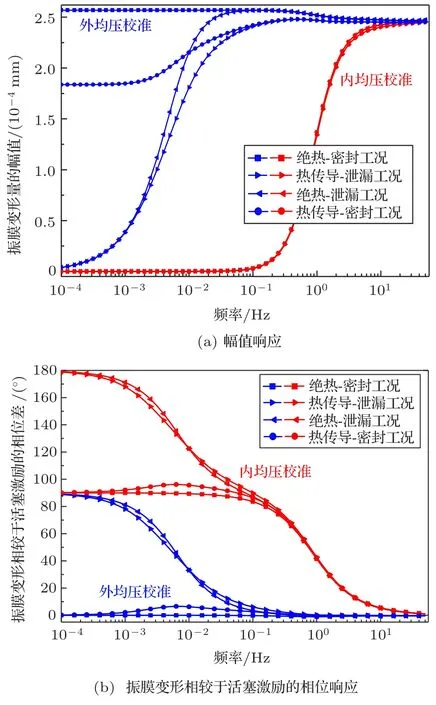
图7 不同工况校准声压激励下的振膜变形响应Fig.7 Frequency responses of diaphragm deformation excited by calibration pressure under different conditions

在图7(b)中发现，振膜变形相较于活塞激励的相位响应伴随着振膜变形幅值的变化而变化。在内均压校准过程中，当泄漏工况下的校准声压与后腔声压作用在传声器振膜上时，随着频率的降低，振膜变形相较于活塞激励的相位超前量趋于180°。在外均压校准声场中，振膜变形相较于活塞激励的相位超前量在极低频率下趋于90°。但在0.1～10 Hz的频段内传声器产生了较小的相位滞后，主要是由振膜将后腔中空气通过均压孔推向外界大气而引起的。

2.2 传声器灵敏度的幅相频响应

进一步地，研究考虑泄漏与热传导效应的校准声压对传声器次声段灵敏度响应的影响。传声器的幅值灵敏度定义为传声器的输出电压(等效于振膜变形)与校准声压的比值[15]，传声器的相位灵敏度是校准声压相较于传声器输出电压的相位偏差，传声器的归一化幅值灵敏度响应与相位灵敏度响应如图8所示。

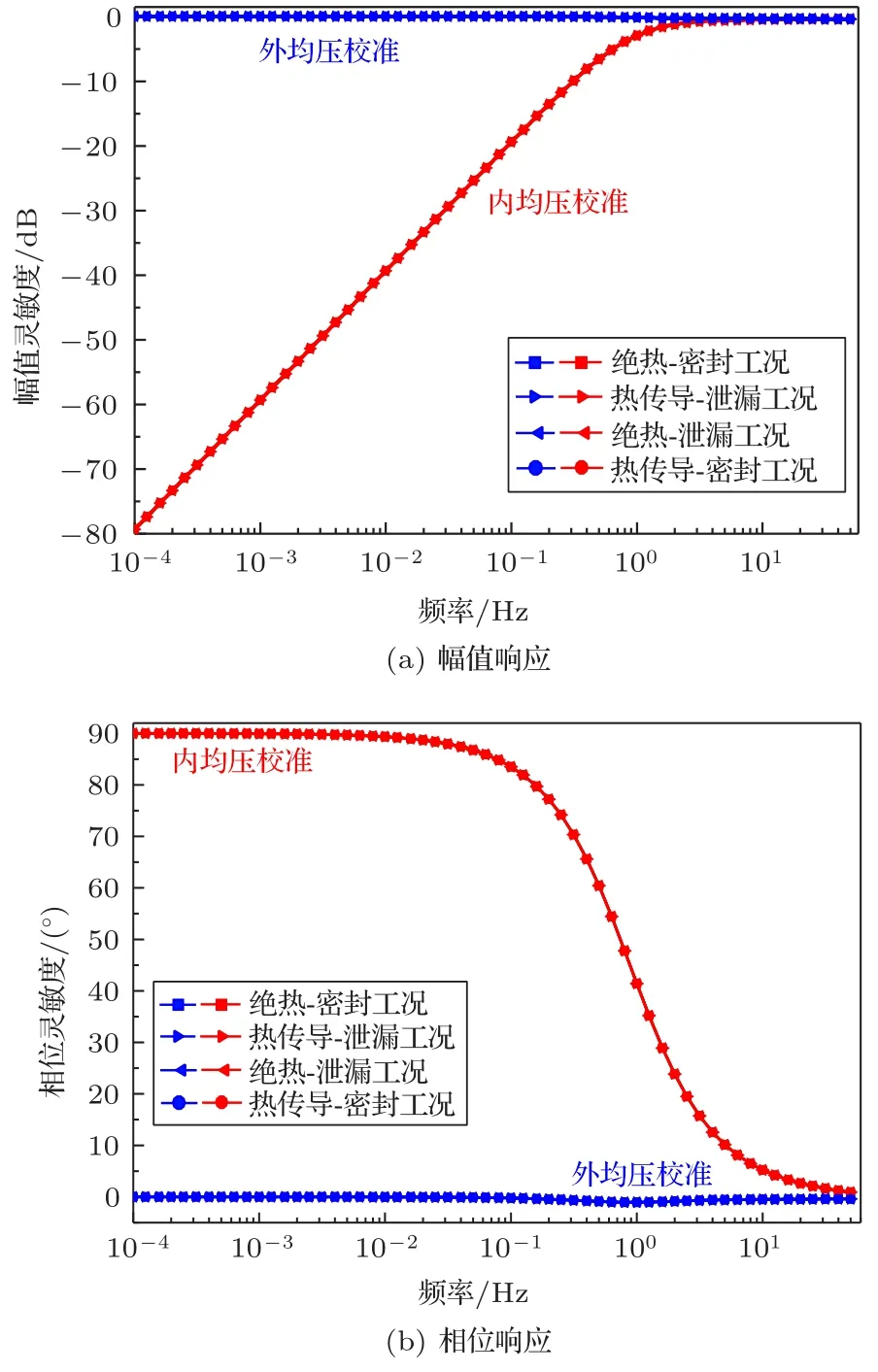
图8 不同工况校准声压激励下的传声器灵敏度响应Fig.8 Frequency responses of the microphone sensitivity excited by calibration pressure under different conditions

从图8可以发现，传声器的灵敏度幅值受内外均压声场的控制，但不受活塞发生装置校准腔的泄漏和热传导效应的影响。外均压校准声场中的传声器灵敏度幅值与相位响应均相对平直，相位灵敏度仅在中频段出现了较小的相位滞后。而内均压校准声场中的灵敏度幅值在次声段下急剧衰减，在极低频率下，相位灵敏度会出现90°的相位超前。幅值灵敏度与Frederiksen等[7]电声等效模型得出的结果一致，相位灵敏度趋势是首次给出。

3 实验验证

3.1 原级校准平台简介

根据第2节对传声器灵敏度幅相频响应的仿真结果分析知，传声器在内外均压校准模式下会出现不同的灵敏度响应。为了验证内外均压校准模式下传声器灵敏度幅值与相位响应的差异，基于搭建的活塞发生器原级校准平台对传声器灵敏度进行内外均压校准。对传声器校准用的活塞发生器原级校准平台结构如图9所示，校准平台主要设备参数如下：

图9 活塞发生器原级校准平台的主要结构Fig.9 Main structures of the pistonphone primary calibration platform

(1)隔振基础：光学平台，台面1200 mm×900 mm×50 mm，支撑架1180 mm×580 mm×700 mm；

(2)松下MINAS A6家族伺服电机(MSMF102 L1H6M)：额定转速：3000 r/min(50 Hz)，电压规格：200 V，额定输出：1000 W，额定电流：6.6 A，额定转矩：3.18 Nm，最高转速：5000 r/min；

(3)伺服驱动器(MDDLT55SF)：速度控制，脉冲数：23 bit(8388608分辨率)，响应频率：3.2 kHz，电源电压：单相/三相200 V；

(4)激光测振仪：振动位移测量范围：0.1µm～100 mm，位移分辨率：2 pm，频率范围：0～10 MHz，输出信号：模拟输出，输出电压范围：±2 V(1 MΩ)±1 V(50 Ω)，激光波长：633 nm，阻抗：50 Ω；

(5)活塞发生器：校准腔内径：130 mm，校准腔长度：393 mm，活塞外径：65 mm，泄漏时间常数：26.8 s；

(6)传声器：PCB-378A07次声传声器频率范围：0.13 Hz～20 kHz(±2 dB)、灵敏度：5.8 mV/Pa、均压孔：后置，CHZ-213驻极体传声器：频率响应20 Hz～20 kHz、灵敏度：50 mV/Pa。

3.2 次声传声器与低频前置放大器组件的内外均压原级校准

为了验证传声器次声段灵敏度响应的差异，基于原级校准平台对PCB-377A07预极化次声传声器与PCB-426E01前置放大器(下限截止频率<0.9 Hz)的传声器组件进行0.1～20 Hz频率范围内的声压灵敏度级内外均压校准实验。采用PCB-480C02信号调理器(工作频率为0.05～500 kHz)对传声器组件供电，避免了数据采集卡的电气衰减对灵敏度响应的影响。计算各频率下的传声器输出电压与激光测振仪采集的活塞位移之间的比值，得出活塞恒定位移激励为1 mm时的传声器输出电压幅值。其中，修正后传声器的声压灵敏度级的表达式为[16]

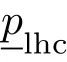
传声器的相位灵敏度可以等效为被校传声器的输出电压相较于位移激励的相位与校准腔内泄漏与热传导耦合修正量的相位之间的差值。根据公式(3)与相位灵敏度的等效定义分别计算内外均压校准模式下修正后的传声器声压灵敏度级幅值与相位响应，如图10所示。

从图10可以看出，在外均压校准模式下，0.1 Hz处的声压灵敏度衰减量达到−3 dB，能够确定出PCB-378A07次声传声器组件的下限截止频率为0.1 Hz。但是由于前置放大器的下限截止频率小于0.9 Hz，即前置放大器的电压提前衰减会造成内外均压校准机制下的传声器灵敏度幅值衰减并伴随产生相位超前，使内外均压校准得出的声压级灵敏度响应差异并不明显。

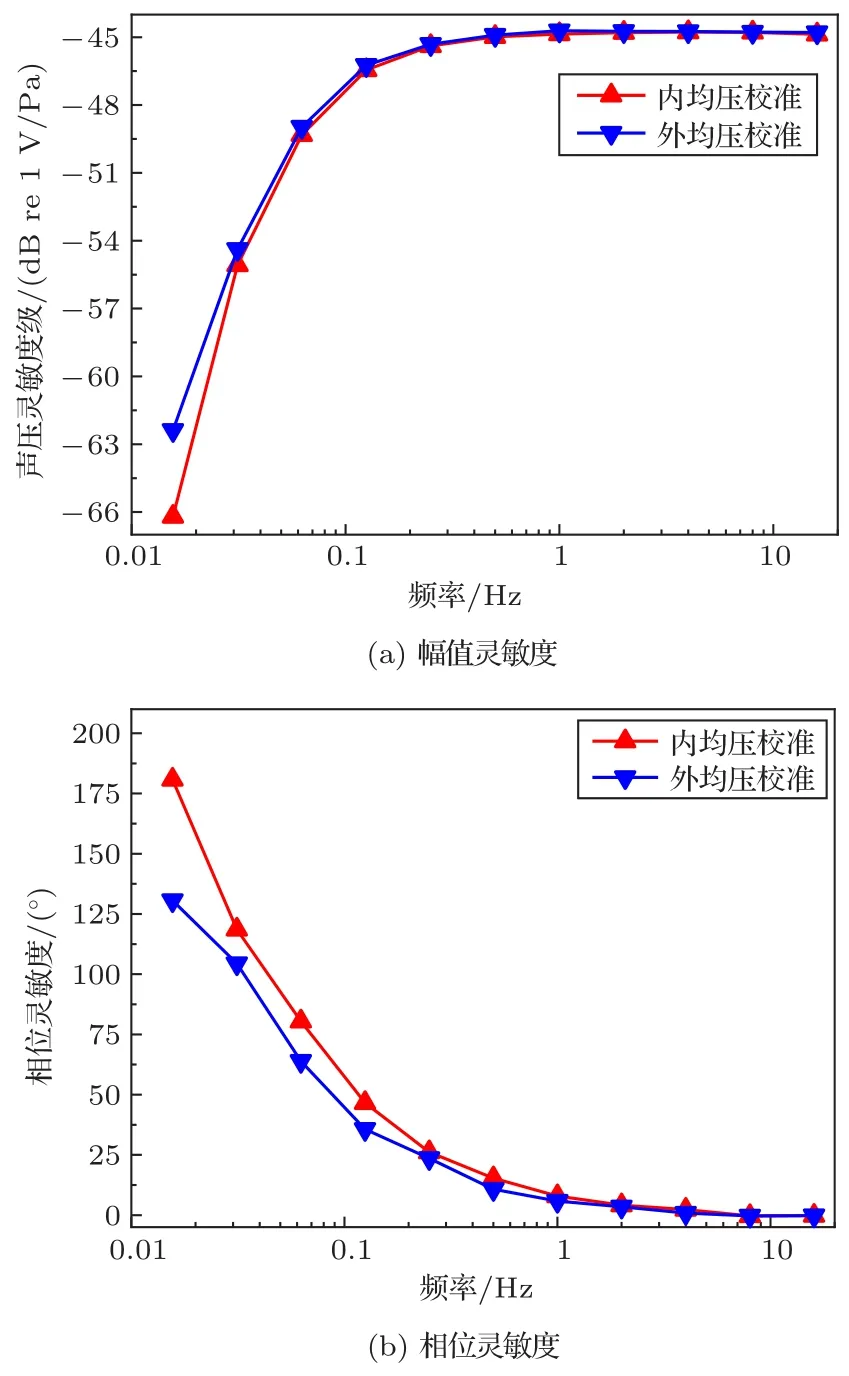
图10 次声传声器组件在内外均压校准模式下的灵敏度响应Fig.10 Sensitivity response of infrasound microphone assembly for vent in field and vent out field calibration modes

3.3 CHZ-213传声器与低频前置放大器组件的内外均压原级校准

根据第3.2节分析知，PCB-378A07次声传声器组件在0.9 Hz以下的频段内受前置放大器的电气衰减的影响，造成内外均压校准模式下的灵敏度响应差异不明显。为了解决此问题，选用下限截止频率高于PCB-377A07的普通传声器CHZ-213配合PCB-426E01前置放大器在0.1～20 Hz内进行内外均压校准，依然采用PCB-480C02信号调理器对传声器组件供电，分别采集内外均压校准模式下传声器组件的输出电压。根据公式(3)和相位灵敏度的等效定义分别计算修正后的传声器声压灵敏度级幅值与相位响应，如图11所示。

在图11中，发现内外均压校准模式下传声器次声段灵敏度幅值响应存在显著差异，且传声器输出电压的相位超前于校准声压的相位。但在0.9 Hz以下的频段内，传声器的灵敏度受到前置放大器的电气衰减特性的影响，使在内外均压校准模式下实际校准得到的传声器组件灵敏度幅值与相位响应与仿真得到的灵敏度响应略有差别。此外，由于CHZ-213传声器没有设置均压孔，其在校准过程中，主要通过连接螺纹进行泄漏，传声器的泄漏效应在校准过程中并不明显，造成传声器的下限截止频率较小，即受前置放大器电气衰减特性的影响明显。在今后的研究中会考虑对CHZ-213传声器开设均压孔以进一步验证内外均压校准机制下灵敏度响应的差异。

图11 次声传声器组件在内外均压校准模式下的灵敏度响应Fig.11 Sensitivity response of microphone assembly for vent in field and vent out field calibration modes

4 讨论

基于COMSOL Multiphysics仿真软件中的热黏滞声学模块，对基于速度激励边界下在校准腔和传声器后腔内产生的声压变化分别进行了独立数值模拟。通过将数值模拟结果与理论解析模型进行对比验证发现，热传导效应造成的压力衰减仅为−3 dB，且在中频段会产生较小的相位超前。而泄漏效应造成的压力损失较为明显，在极低频率下，声压的泄漏损失相较于活塞激励的相位超前量趋于90°。因此在校准前，应确定校准腔的低频测量下限，对腔内压力泄漏与热传导损失的幅值与相位进行提前修正。

根据双重耦合机制，在COMSOL Multiphysics数值模拟软件中对传声器进行了多物理场联合仿真，研究不同泄漏与热黏滞边界条件下的校准声压对传声器振膜变形与灵敏度幅相频特性的影响。仿真结果发现，内外均压校准声场下传声器灵敏度的幅相频响应存在明显差异。不同工况中的校准声压会影响内外均压校准声场下传声器振膜变形的响应，但传声器灵敏度不受校准腔内泄漏与热传导效应的影响。

基于搭建的活塞发生器原级校准平台分别对PCB-377A07次声传声器与PCB-426E01前置放大器、CHZ-213传声器与PCB-426E01前置放大器两套传声器组件进行了内外均压校准，通过实验手段初步发现了内外均压校准声场下传声器次声段灵敏度幅值与相位响应的不同。

5 结论

本文基于活塞发生器原级校准技术揭示了校准腔与传声器后腔内声压泄漏与热传导损失的幅值与相位特性变化规律。基于声压的泄漏与热传导耦合衰减模型，在COMSOL多物理场仿真软件进行对比验证，在频域模块下对校准腔和传声器后腔内的声场特征进行了数值仿真，创新性地提出了模型比较法，准确量化了次声段校准过程中泄漏、热传导独立修正量与耦合修正量的幅值与相位响应。进一步地对传声器的次声段灵敏度校准过程进行了联合数值模拟，揭示了泄漏、热传导、内外均压等多物理效应在灵敏度校准过程中的误差机理。基于搭建的原级校准平台分别对PCB-377A07次声传声器与PCB-426E01前置放大器、CHZ213传声器与PCB-426E01前置放大器两套传声器组件进行了内外均压校准，通过实验手段初步揭示了内外均压校准模式下幅值灵敏度响应的明显不同以及相位灵敏度超前的规律。