考虑目标视线角指标的近距离接近位姿一体序列凸规划

周 鼎，陈洪波，李顺利

（1.上海宇航系统工程研究所，上海，201109；2.哈尔滨工业大学航天学院，哈尔滨，150001；3.中山大学系统科学与工程学院，广州，510275）

0 引 言

针对服务航天器近距离接近非合作目标的制导与控制问题，目前的挑战主要来自以下几个方面：a）传统的地面在回路的方案不能满足中高轨道接近任务的自主性需求；b）目标的非合作特点要求服务航天器自身进行相对测量，传感器的指向约束使得位姿耦合，因而需要进行位姿一体轨迹规划；c）高维状态的非线性和位姿耦合的路径约束使得规划问题的求解变得更加困难[1～3]。近年来，由于计算制导与控制技术[4]的发展，凸规划方法以其良好的收敛性和全局最优性保证逐渐被应用于交会对接[5]、行星软着陆[6]及火箭垂直起降[7]的自主制导。本文旨在对凸规划方法进行应用扩展，利用序列迭代求解近距离接近的位姿一体轨迹规划问题。

凸规划方法应用的主要障碍是处理规划问题中的非凸约束。针对自主交会问题，文献[5]将接近过程的障碍区域近似为旋转超平面，并将原问题松弛为一系列二阶锥规划进行迭代求解。在对偶四元数描述的六自由度行星着陆制导中，控制约束通过引入维度增广被无损凸化，相关指向约束被近似为二阶锥约束，然后通过凸规划方法求解以进行模型预测控制[6]。为减小凸化近似带来的人工不可行性，一种基于轨迹偏差的信赖域约束被引入序列迭代算法中以促进收敛，该方法可有效应对火箭垂直起降制导中气动参数带来的不确定性[7]。

在能量-最优的基础上，本文考虑目标视线角-最小性能指标，使得视觉传感器光轴尽可能对准目标以保证良好的相对导航质量。首先建立近距离接近位姿一体规划的最优控制问题，然后对其中的非凸指标函数、非线性姿态动力学、位姿耦合视场角约束、碰撞规避约束进行凸化，并通过信赖域约束的序列迭代算法进行求解。最后，通过数值算例验证了目标视线角-最小性能指标及序列凸化方法的有效性。

1 问题描述

本节主要描述近距离接近位姿一体规划的最优控制问题，主要包括系统动力学、路径约束以及包含目标视线角的性能指标。

1.1 坐标系统

图1 坐标系统Fig.1 Coordinate System

1.2 系统动力学

近距离接近的系统动力学由服务航天器与目标卫星之间的质心相对运动模型、服务航天器姿态动力学及其相对于L 系的姿态运动学组成。

1.2.1 质心相对运动模型

考虑近圆轨道上的目标卫星，服务航天器与目标位置之间的质心相对运动模型可由CW 方程进行描述，写成矩阵形式如下：

式 中 xp为 平 动 运 动 状 态 ，xp= [ ρT, vT]T=[ x , y , z , vx, vy, vz]T； up为 控 制 加 速 度，up=[ ax, ay, az]T； Λp为动力学矩阵； Gp为控制矩阵，分别表示为

式中 nref为参考轨道平均角速率。

1.2.2 姿态动力学模型

假设服务航天器为刚体，其姿态动力学方程可表示为

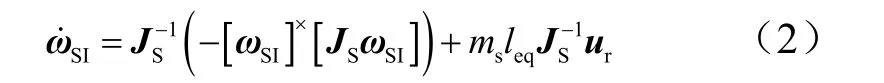
式中 ωSI为服务航天器惯性角速度在S系中的分量列阵， ωSI=[ωx,ωy,ωz]T； JS为其转动惯量在S系中的分量矩阵，相应的主轴惯量为 Ixx, Iyy和 Izz；a×表示向量a 的反对称矩阵。为了便于后续性能指标和约束的描述，通过服务航天器的质量sm 和一个特征长度 leq定义了一个如下的等效控制加速度：

式中ST 表示控制力拒矢量在S 系中的分量列阵，TS=[Tx, Ty, Tz]T。

1.2.3 姿态运动学模型

考虑接近过程中可能存在较大范围的姿态机动，为避免可能出现的姿态解算的奇异，采用修正罗德里格参数（MRPs）来描述空间指向，定义服务航天器本体相对于参考轨道坐标系的姿态 MRPs 为σSL=[σ1, σ2,σ3]T，通过其表示的从L 系到S 系的姿态变换矩阵为

式中 In为n 阶单位矩阵；相应地，以MRPs 形式描述的姿态运动学方程为

式中 ωSL为S 系相对于L 系的角速度在S系中的分量列阵， ωSL=[ω1, ω2,ω3]T，可通过如下关系式计算：

式中 ΩL=[ 0 ,0,nref]T。

1.3 路径约束

在接近非合作目标的过程中，服务航天器的位姿轨迹需要满足传感器视场角、碰撞规避及控制能力限制等路径约束。

1.3.1 传感器视场角约束

为保证持续的相对导航，在近距离接近过程中，位姿轨迹需要使目标一直处于服务航天器的传感器视场内，如图2 所示，相应的约束可表示为

式中 β 为目标视线角；b 表示传感器的安装位置在S系中的分量列阵；d 表示传感器光轴方向矢量在S系中的分量列阵； βFOV为传感器视场角。注意到，非线性项使得位姿状态耦合到一起。

图2 视场角约束及碰撞规避约束示意Fig.2 Illustration of Constraints On Field of View and Collision Avoidance

1.3.2 碰撞规避约束

在最终与目标进行停靠或对接操作前，服务航天器必须避免与目标发生任何碰撞，所以质心相对距离必须大于安全距离 rsafe，如图2 所示，该约束可表示为

本文中考虑服务航天器和目标的外形尺寸，安全距离 rsafe=6.6 m。

1.3.3 控制能力约束

考虑服务航天器的敏捷机动能力，其位姿控制均通过推力器来实现，其物理特性（如最大推力等）使得可用的控制力/力矩在有限的范围内，相应地施加到控制加速度上的约束可表示为

1.4 性能指标

根据上述系统动力学和路径约束的描述，将服务航天器的姿态运动状态定义为，相应的位姿状态和控制加速度可分别表示为和

假设服务航天器为全驱动控制，能量成本以控制u 的1L-范数形式来度量[8]，对于给定的时间区间 [ t0,ft] ，能量-最优问题的性能指标为

此外，虽然有路径约束（4）来保证接近过程中目标处于传感器视场内，但考虑视场边缘的畸变和噪声会显著增加从而影响相对导航精度，接近过程的位姿轨迹应尽可能使目标视线矢量处在传感器光轴附近，即目标视线角尽可能小，相应的性能指标为

式中 β∈( -π /2,π/2)。

1.5 最优控制问题

综上所述，考虑能量+目标视线角的复合性能指标，服务航天器近距离接近位姿一体规划的最优控制问题可表示为

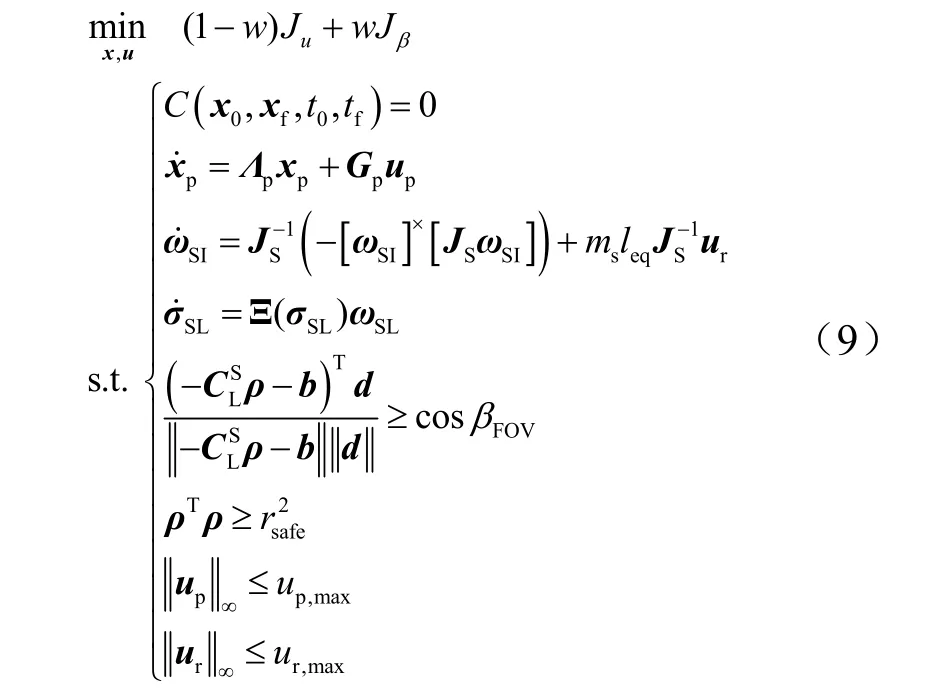
式中 w 为相对权重系数，w∈[0,1]； C （ x0, xf, t0,tf）表示边值条件相关的函数，终端状态 xf利用最终的停靠或对接条件进行计算。

2 问题的凸化松弛

式（9）描述的问题指标函数和约束中均包含非凸项，在利用凸规划方法求解前需要进行凸化松弛，并通过离散化将无限维的连续时间微分约束问题转化为有限维的代数约束凸规划问题。

2.1 视线角指标的凸化

定义关于状态轨迹x 的函数：

式中 Cρ为相对位置状态提取矩阵，，其使得 ρ = Cρx。由于光轴方向矢量为单位向量，即所 以 gβ( x ) =- cosβ。 注 意 到， -cosβ是 关 于β∈( - π /2,π/2)的凸函数，所以视线角对应的性能指标（式（8））可等价地表示为

在参考状态轨迹x~ 附近通过一阶泰勒展开对性能指标（11）近似可得：

2.2 系统动力学线性化与离散化

系统动力学中的质心相对运动方程（式（1））原本就是线性的，所以这里主要对姿态运动方程进行线性化。

式（2）、（3）描述的姿态动力学和运动学可以统一地写成关于姿态运动状态的微分方程：

在参考轨迹附近对式（13）中的 fr(rx) 进行一阶泰勒近似可得：

所以，姿态运动方程（13）可近似地线性化为

将给定的飞行时间区间 [ t0,ft] 离散成K 个子区间，利用零阶-保持方法对连续-时间控制 u( t) 进行离散化：

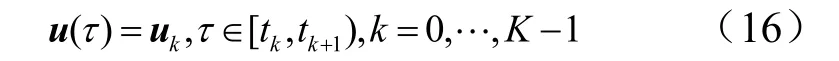
2.3 路径约束凸化

在1.3 节描述路径约束中，视场角和碰撞规避约束均为非凸约束，本节将对它们进行凸化处理；而控制约束为锥约束，原本就是凸的，无需再进行凸化。

2.3.1 视场角约束凸化

根据函数 gβ( x )的定义，式（4）描述的视场角约束可以等价地改写成如下形式：

2.3.2 碰撞规避约束的凸化

式（5）描述的碰撞规避约束可等价改写为

2.4 信赖域约束

上述对性能指标和约束的松弛处理都是在参考轨迹x~ 附近进行，所以求解的轨迹与参考轨迹之间的偏差不能过大，否则松弛的问题无法逼近原问题的非凸性。为此，定义如下变量来度量轨迹的偏差：

并针对离散后的问题引入信赖域约束以确保偏差有界，即：

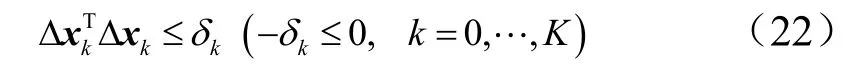
式中kδ 表示信赖域半径的平方。该约束在性能指标中对应的罚项可表示为

2.5 离散凸化子问题

经过上述对性能指标及约束的凸化处理，连续-时间的非凸原问题（式（9））可在参考状态轨迹x~ 附近松弛为如下离散的凸化子问题：

式中 xi和 xf分别为初始状态和终端状态。

3 序列凸化算法

本节提出通过序列求解凸化子问题（式（24））对非凸原问题（式（9））进行逼近的迭代算法。

首先，给出初始迭代的参考轨迹猜想。与序列二次规划[9]等非线性规划方法相比，序列凸化方法对初始猜想的敏感度较低，为方便迭代的快速启动，本文按如下方法选取初始参考轨迹：

式中 x(j)表示第 j ( j= 0,1,2,… ) 次迭代求解凸化子问题（式（24））的状态轨迹解。从第1 次迭代开始，第j 次迭代中用于问题凸化处理时各系数矩阵或常数向量计算的的参考轨迹为 x(j-1)。

理论上当Δx =0 时原问题（式（9））到达一个最优解[10]，但实际数值求解时需要设置一个序列迭代过程的停止准则，即：

式中 Δx(j)= x(j)- x(j-1), ( j ≥1)；εx为容许的状态轨迹偏差上界。

接下来给出序列凸化算法。

b）令j= 1，只考虑系统动力学及控制约束求解凸化子问题（式（24））得到解

c）令 fsol= False ；

d）当 fsol== False 时执行下列程序；

e）更新迭代次数j = j+ 1；

h）计算状态轨迹偏差 Δx(j)= x(j)-x(j-1)；

j）fsol=True；

k）子命令结束；

l）程序结束；

4 数值算例及分析

本节对上述求解含视线角指标的近距离接近位姿一体规划问题的序列凸化方法进行数值算例仿真及分析。仿真环境为Matlab R2014a（×64），计算机主频2.30 GHz，内存4 GB。底层凸化子问题的通过CVX软件进行求解。目标卫星及服务航天器的物理参数见文献[2]，其中传感器视场角 βFOV=25°，允许的最大控制力为8 N，最大控制力矩为10 N·m。飞行时间区间设置为[0，360] s，根据停靠条件计算服务航天器边值状态如表1 所示。

表1 服务航天器的边值条件Tab.1 Boundary Conditions of the Service Spacecraft

序列凸化的参数设置如下：离散区间数K=60，精度要求xε=1×10-7，性能指标相对权重w=0.5，信赖域权重系数wδ=1.0。

经过5 次凸化子问题求解后，迭代过程满足停止准则，信赖域半径达到9.6×10-10，求解过程耗时102 s。如图3 所示，与单独的能量-最优相比，将视线角作为优化指标可有效降低机动过程中目标视线角的峰值，使目标视线矢量保持在传感器光轴附近，有益于相对导航的成像质量。

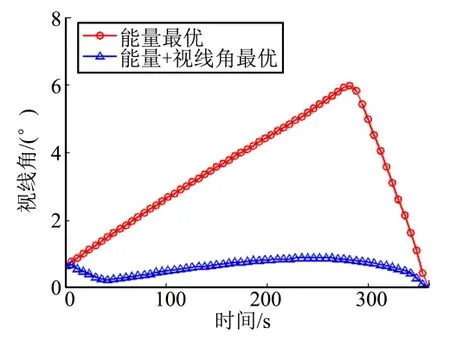
图3 不同性能指标下目标视线角Fig.3 Variations of LOS Angle of the Target with Different Performance Index

图4 ～12 给出规划的位姿状态变化、约束满足情况及控制力/力矩。机动过程位姿状态变化平稳，控制力/力矩均未超出容许上界，最大控制力为7.999 N，最大控制力矩为0.376 N·m，控制呈现明显的分段常值特征。相对速度最大为0.135 m/s，整个机动过程中速度大小比较稳定，无明显振荡，惯性姿态角速度最大值为0.095 (°)/s。目标视线角最大值为0.88°，远小于βFOV，位姿状态满足视场角约束。接近过程相对距离变化一直大于安全距离，表明位置状态满足碰撞规避约束。

图4 相对位置分量Fig.4 Variations of Relative Positions

图6 相对距离Fig.6 Variations of Relative Distance

图7 相对速度Fig.7 Variations of Relative Distance

图8 控制力分量Fig.8 Variations of Control Forces

图9 惯性姿态角速度分量Fig.9 Variations of Inertial Angular Velocities

图10 惯性姿态角速度Fig.10 Variations of Inertial Angular Rate

图11 相对于轨道系的MRPFig.11 MRP with Respect to LVLH

图12 控制力矩分量Fig.12 Variations of Control Torques

如图13 所示，在不设置停止准则精度要求的情况下，序列凸规划算法经过6 次迭代后，信赖域半径收敛到2.1×10-10；相比之下，在不考虑信赖域约束的情况下，算法不能收敛，信赖域半径在1×10-2附近振荡，如图14 所示。可以看出，信赖域约束能够有效改善序列凸化方法求解非凸约束的高维位姿一体规划问题的收敛性。

图13 信赖域约束序列凸规划算法的收敛过程Fig.13 Convergence Process of SCP with Trust Region Constraints

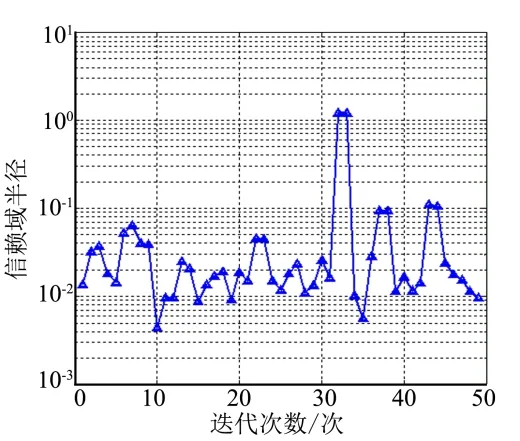
图14 无信赖域约束序列凸规划算法的迭代过程Fig.14 Iterations of SCP without Trust Region Constraints

通过对信赖域权重系数的调整来观察其对序列凸规划算法收敛性能的影响。如图15 所示，随着信赖域权重从1×10-2量级逐渐增加到1×103量级，收敛的信赖域半径从1×10-8量级减小到量级1×10-11，整体上精度逐渐提高；相应地，收敛所需的迭代次数也呈现下降趋势。由此可见，适当提高信赖域权重有助于改善收敛性能。

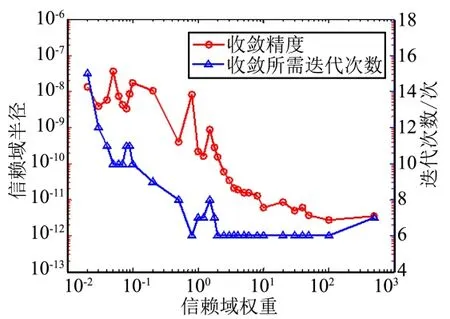
图15 信赖域权重的变化对收敛性的影响Fig.15 Effects of Trust Region Weight on Convergence

然而，另一方面，随着信赖域权重的增加，规划的位姿状态对应的目标视线角最大值逐渐增大，如图16 所示，使得指标函数中的视线角项失去效果。所以，在实际应用中选取信赖域权重时需要注意性能指标与收敛性之间的权衡。

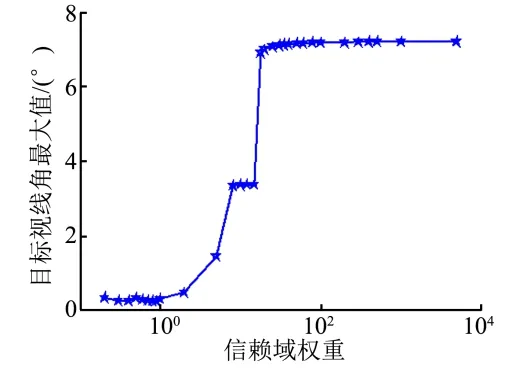
图16 信赖域权重对视线角峰值的影响Fig.16 Effects of Trust Region Weight on Peak LOS Angle

5 结 论

本文针对服务航天器自主接近非合作目标的任务，考虑相对导航需求，提出了考虑目标视线角性能的近距离接近位姿一体规划问题，设计了信赖域约束的序列凸规划方法进行求解。算例仿真表明，视线角指标可有效降低机动过程中目标视线角的峰值，使目标视线矢量保持在传感器光轴附近；信赖域约束的序列凸规划方法可有效求解非凸约束的高维位姿规划问题，将凸规划方法从三自由度的自主交会轨迹规划扩展到了六自由度的近距离接近阶段。此外，通过对比仿真可以看出，适当提高信赖域权重系数有助于提高序列凸规划算法的收敛性能，但需要与最优控制问题的性能指标进行权衡。