基于自动改进Kriging 方法的导弹舱体结构可靠性分析

秦 强，赵朋飞，张文伟，冯蕴雯

（1.航天科工防御技术研究试验中心，北京，100854；2.西北工业大学航空学院，西安，710072）

0 引 言

导弹的舱体结构和其他弹上设备一样，是导弹系统的重要组成部分[1,2]。各个舱段、空气舵和燃气舵等各种翼面、各舱段之间和舱段与翼面之间的连接件构成了舱体主要结构。在执行机动动作过程中，导弹舱体结构会因受到发动机推力、自身重力、振动应力和惯性力等载荷的共同作用导致强度失效[3]。传统的结构设计法通过引入安全系数以表征导弹工作中的各种不确定因素对结构的影响。然而这种方法在很大程度上依赖于设计者的经验，具有一定的不确切性或盲目性。在导弹结构上采用此方法不仅不能深入分析影响导弹结构可靠性的不确定因素而且不能完全杜绝结构失效，相反，会造成导弹结构重量的增加，导致导弹射程减小。因此，深入研究导弹舱体结构关键设计参数对其影响程度并且保证导弹结构安全可靠是导弹设计过程中需要迫切解决的关键问题。

对于导弹结构，结构可靠性方法的显著特点是能够减少质量，并能降低成本和提高性能。近年来，众多学者开展了导弹结构可靠性分析研究。文献[3]在确定性分析的基础上，研究了某型导弹舱段连接结构强度的可靠性；文献[4]和文献[5]采用Patran/Nastran 软件建立了导弹吊挂结构参数化模型，并对其开展了可靠性即灵敏度分析；文献[6]将某导弹空气舵肋梁结构的尺寸以及弹性模量作为随机变量，在将最大变形作为输出响应量的基础上构建极限状态方程，进而采用自主学习Kriging 方法得到了结构的失效概率。通过以上研究可知，由有限元方法得到的结构最大应力或最大变形等响应量是舱体材料性能、外部载荷以及结构尺寸等参数的隐式表达。然而，若分析导弹舱体结构可靠性，则应构造一定的函数表达式，建立输出响应量与输入参数之间的显式关系，进而得到结构的极限状态方程。开展舱体结构有限元分析时，可以选择

ABAQUS 、 ANSYS 、 MSC.PATRAN/NASTRAN 、HYPERWORKS 等有限元分析软件[7]。其中，ANSYS Workbench 的六西格玛（Six Sigma）分析模块内嵌了多种代理模型可以建立舱体结构输出响应量与输入参数之间的函数关系，包括人工神经网络、Kriging 模型、完全二次多项式响应面函数等。文献[8]～[11]分别利用该模块对圆盘造球机、甘蔗切割器上臂轴、门式卸车机以及机床主轴等结构进行了可靠性分析，充分表明了该模块在可靠性分析中的有效性。以上文献在建立响应面时用到了神经网络模型与二次多项式响应面方法，这些方法只能通过已经生成的样本集得到相应的响应面函数，而且仅能得到预测点的预测值[12]。与神经网络与二次响应面法不同的是，Kriging 模型在提供预测点的预测值的同时能够得到该点的方差[13]。近年来，国内外学者依据Kriging 模型这一特性在其主动学习方面做了大量的研究工作，并应用于结构可靠性分析领域[14]。在通过Kriging 方法拟合响应面的过程中，根据Kriging 模型的特性可以得到对响应面拟合性能产生最大影响的点，并将其作为新的设计点加入到原始的训练集中，这样通过一定的规则反复迭代不断地扩充训练样本集，达到增强Kriging 模型拟合性能的目的，直到满足收敛要求。这种主动学习的Kriging 方法在 ANSYS Workbench 中称为自动改进 Kriging（Auto-Refinement Kriging，AR-Kriging）方法，其自带的AR-Kriging 分析模块为结构可靠性分析提供了更为便捷有效的手段。

本文利用参数化建模方法在ANSYS Workbench中构建导弹舱体结构模型，然后采用最优空间填充设计抽样获取多组样本点并通过有限元分析得到各样本点对应的响应量，结合AR-Kriging 方法生成响应面并开展参数灵敏度分析以探究结构尺寸、材料性能、外部载荷等参数对舱体结构的影响程度，进而通过六西格玛分析评估舱体结构可靠性。

1 Kriging 模型基本理论

Kriging 模型是一种插值模型，通过参数线性回归模型叠加一个非参数随机过程而成[12～14]。模型表达式为

式中 Γ(β , x) 为多项式回归模型；β 为回归系数向量，β=[β1,...,βp]T；fT( x) 为变量 x 的多项式，fT( x) =[f1(x),f2(x),...,fp(x)]T； z ( x) 为均值为零、方差为σ2的随机高斯过程。在设计空间不同位置处，这些随机变量之间的相关性通过协方差表述为

式中 ℝ ( xi, xj; θ )为 xi与xj的相关函数。在经典Kriging模型中，常见的相关函数模型有指数模型、高斯模型、线性模型、样条函数模型等，而最为常用的函数模型是高斯模型：

式中 θ 为参数向量，θ=[θ1, θ2,···, θm]T；m 为输入向量第m 维元素；M 为输入向量的总维度。

式中 F 为N0×1 的单位矩阵；N0表示训练样本点个数。由式（1）～（3）可知，由回归系数向量β、随机过程的方差σ2以及参数向量θ 可以完全定义一个Kriging 模型。而由式（4）、式（5）可知，回归系数向量β 与随机过程的方差 σ2依赖于参数向量 θ。因此，在构造Kriging 模型时，首先应根据样本点求出参数向量θ，这一步骤可以通过最大似然估计实现，即：

此时，对于预测点x 的预测值ˆ( )G x 的均值和方差分别为

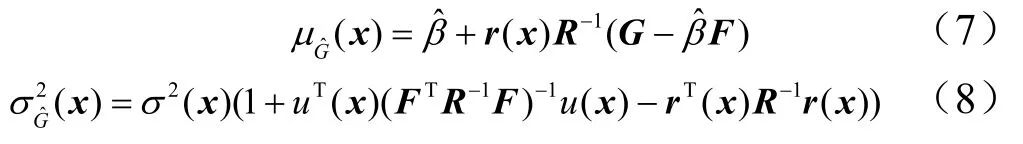
2 舱体结构及参数化建模

在ANSYS Workbench 中构建舱体结构，在其前后端面各有4 个孔，用于链接双头螺栓；在舱体中部开有1 个矩形孔，如图1 所示。在设置边界条件时，固定后端面，而施加一定的外载荷与前端面处。通过确定性分析得到舱体结构的应力云图和应变云图，如图2所示。

图1 导弹舱体结构示意Fig.1 Diagram of a Missile Cabin Structure

图2 舱体结构受载云图Fig.2 Stress and Deformation Nephograms

在铸造加工舱体结构过程中，由于仪器设备与量具的精度以及工艺人员的技术水平等外部因素的影响，即使是同一批次舱体结构，在加工成型后仍会存在一定的尺寸差异。因此在对舱体结构开展可靠性分析时将舱体关键尺寸参数考虑为随机变量，包括舱体长度Y1、中部开孔长度Y2、宽度H 以及内径X 等。此外，在考虑舱体材料性能以及加载不均匀性对其结构功能的影响情况下，将材料的弹性模量E 以及加载力F亦作为随机变量。一般情况下，产品尺寸被认为服从正态分布，而在实际情况中，由于装配关系，产品的尺寸存在上限值及下限值，因此属于截断正态分布；通过加载系统可以将外载荷很好地控制在上、下限范围内，因此认为其也服从截断正态分布；一般认为材料的弹性模量服从正态分布。本文涉及的6 个输入随机变量的数字特征如表1 所示。

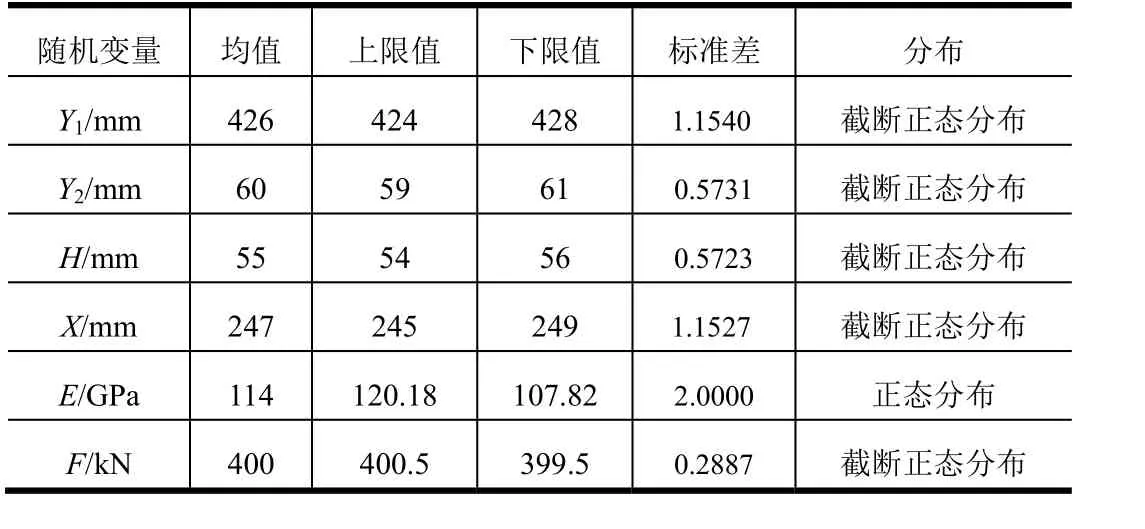
表1 输入变量数字特征Tab.1 Statistical Characteristics of Random Variables

根据以上输入变量的数字特征，在 ANSYS Workbench 中进行设置，即可获得导弹舱体结构参数化模型。

3 基于AR-Kriging 的舱体结构可靠性分析

3.1 随机样本抽样

在ANSYSY Workbench 中，可以选择的抽样方法包括拉丁超立方抽样（LHS）、最优空间填充（OSF）方法、中心复合设计（CCD）抽样以及Box-Behnken抽样等。其中，CCD 以及BOX-Behnken 方法适用于构造经典响应面函数，并且产生的随机样本数与输入变量的个数有关。但是LHS 和OSF 方法产生的样本数与输入变量的个数无关，可以在Workbench 中任意设置，而且OSF 是一种优化的LHS 方法，在设计空间中通过OSF 产生的样本的均匀性要优于LHS 产生的样本[15]。因此，本文根据OSF 抽样出200 个随机样本，这样不仅能够获得足够多的样本训练Kriging 模型，而且可以在后续自动改进过程中生成更优的样本点。

3.2 采用自动改进Kriging 方法构造响应面

在Workbench 中的响应面类型中选择“Kriging”，而在核变量类型选项中有默认选项“Variable”和“Constant”，其中，Variable 表示在式（3）中的参数向量θ 的每一分量均不同，而Constant 表示θ 的每一个分量均相同[15]，本文保持其默认选项。

在Workbench 中利用AR-Kriging 方法构造响应面时，各参数的设置如表2 所示。

表2 AR-Kriging 在Workbench 中的设置Tab.2 The setup of AR-Kriging in Workbench

在ANSYS Workbench 中，AR-Kriging 方法的原理是通过自动改进策略选择特定的改进准则并根据自动优化程序在设计空间中增加更多的设计点以达到自动更新Kriging 模型的目的。在自动改进迭代的每一次循环中，Kriging 模型在全部参数空间范围内对预测相对误差进行评估。而误差预测是一个连续可微的方程。为了得到最优的改进设计点，改进过程通过运行一个基于梯度优化的程序计算这个预测方程的最大值。如果新的候选设计点的预测精度优于设置的允许精度，那么认为该候选设计点是新的设计点。

3.2.1 双输出变量情况

本节将最大应力及最大变形同时作为输出变量，分析AR-Kriging 方法在拟合响应面时的性能。采用AR-Kriging 方法对舱体结构进行分析时，输出变量相对误差随改进样本点数的变化曲线如图3 所示。

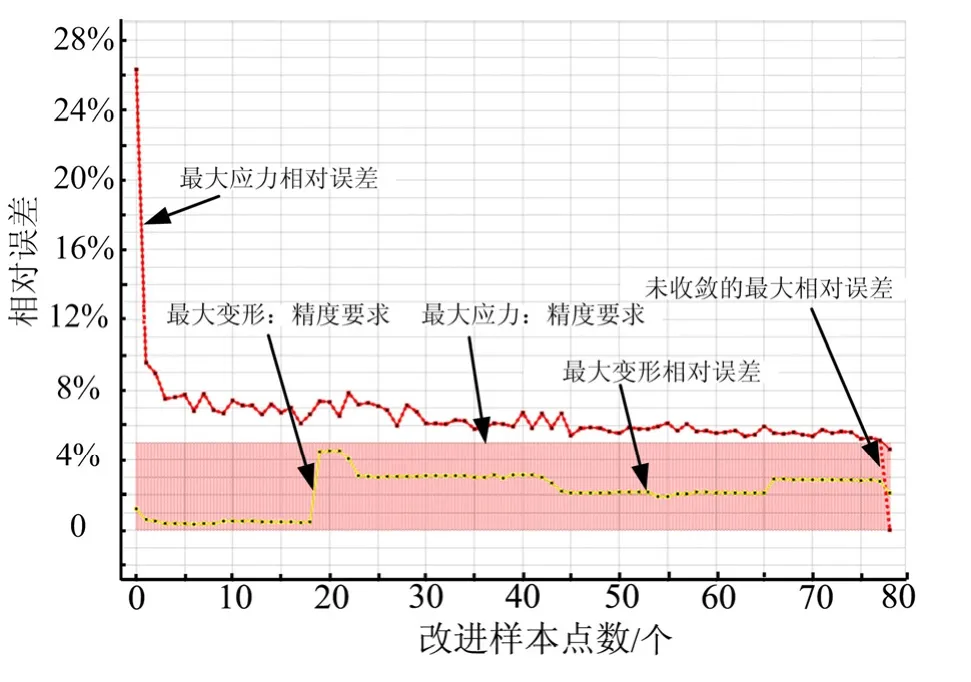
图3 输出变量相对误差随改进样本点数变化Fig.3 The Curve of Relative Error with Design Point

由图3 可以看出，Kriging 模型对最大变形的拟合误差始终能够保持在误差要求范围内，但是当增加到第19 个样本点时，该输出变量的误差从0.5%跳跃至4.5%，此后随着样本点的增加有缓慢下降的趋势。另一方面，最大应力的拟合误差总体上呈现出下降的趋势，当改进样本点增加到第78 个的时候，最大变形的拟合误差降低到 4.6259%，满足收敛要求，此时Workbench 停止继续迭代。

为了对比分析AR-Kriging 模型与原始Kriging 模型的拟合精度，表3 列出了由验证点产生的各种误差值。其中，原始Kriging 模型是通过原始生成的200 个样本点在Workbench 中得到的响应面模型。误差值包括均方根误差（RMSE）、相对均方根误差（RRMSE）、相对最大绝对误差（RMAE）以及相对平均绝对误差（RAAE）。

表3 验证点通过两种Kriging 模型产生的误差对比分析Tab.3 Comparison of the Errors Produced by Two Kriging Models

由表3 可知，对最大应力这一输出变量而言，20 个验证点通过自动改进Kriging 模型产生的RMSE、RRMSE 以及RAAE 相对于由Kriging 模型产生的相应的误差有所减小，但是由AR-Kriging 模型产生的最大变形量的RMSE、RRMSE 以及RAAE 相比于Kriging模型均有不同程度的增加。另外通过表3 还可以看出，由自动改进Kriging 产生的RMAE 高于Kriging 产生的RMAE。以上的数据分析表明，在AR-Kriging 迭代过程中，为了降低最大应力的RMSE、RRMSE以及RAAE是以牺牲最大变形量的拟合精度为代价的，这一情况也可由图3 中的误差收敛曲线看出。

3.2.2 单输出变量情况

由3.2.1 节分析可知，在对双输出变量同时构造响应面时，即使采用Kriging 方法就已经能够对最大变形的拟合达到非常良好的效果，然而不论是Kriging 方法还是AR-Kriging 方法得到的关于最大变形的拟合精度都有待进一步提高。因此本节仅以最大应力为输出变量，对比分析Kriging 方法及AR-Kriging 方法在单输出变量情况下的拟合性能。保持AR-Kriging 参数如表2 所示，最大应力相对误差随改进样本点数的变化曲线如图4 所示。

图4 最大应力响应面相对误差随改进样本点数变化Fig.4 The Curve of Relative Error with Design Point

由图4 可知，在增加11 个样本点的情况下，最大应力的响应面预测误差满足收敛要求，此时Workbench停止继续迭代。相比于图3 可知，大大减小了新的样本的加入，提高了计算效率。表4 列出了由验证点产生的误差值。

表4 最大应力验证点通过两种Kriging 模型产生误差对比分析Tab.4 Comparison of the Errors Produced by Two Kriging Modes

由表4 可知，通过AR-Kriging 方法大大提高了响应面的拟合精度，RMAE 与RAAE 分别从采用Kriging方 法 时 的 132.67% 和 96.399% 降 低 到 了 采 用AR-Kriging 方法时的28.073%和10.451%。由于RMAE与RAAE 分别能够表明Kriging 模型局部以及全局的拟合能力，因此通过AR-Kriging 方法提高了生成的响应面的全局拟合能力。

3.3 舱体结构灵敏度分析

由结构可靠性灵敏度的定义可知，灵敏度数值的绝对值越高表明输入变量对输出变量的影响程度越大。通过选择局部灵敏度（Local Sensitivity）分析6 个输入变量对2 个输出变量的影响程度。舱体结构灵敏度矩形图分别如图5、图6 所示。

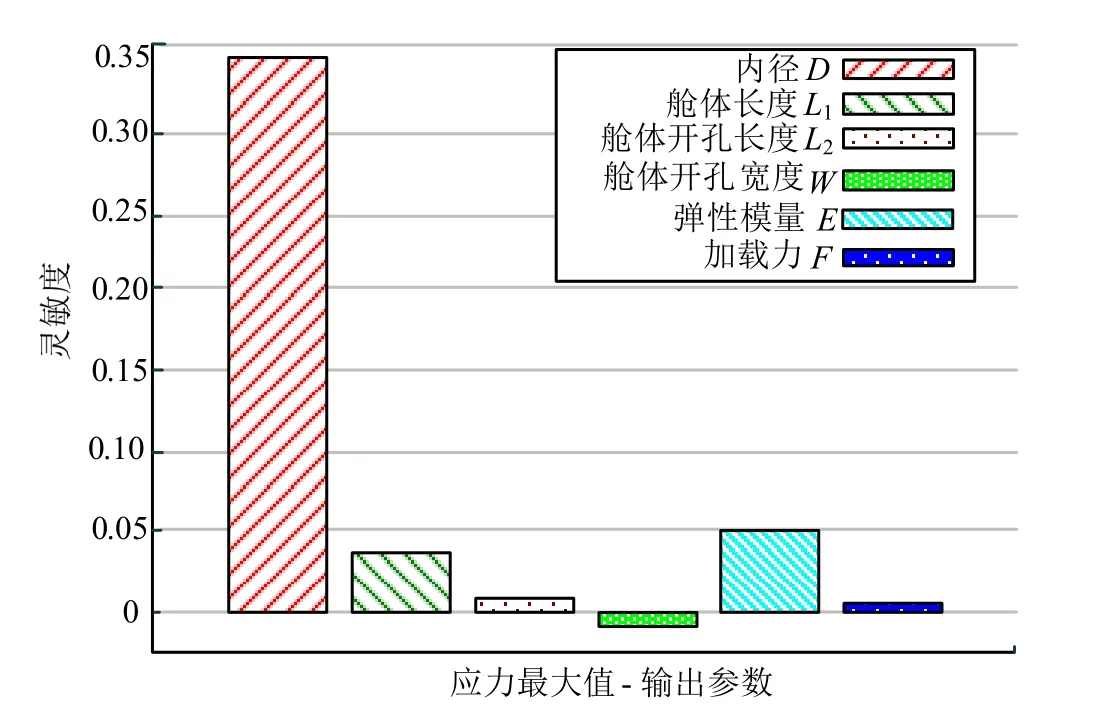
图5 输入变量对最大应力的灵敏度变化Fig.5 Sensitivity of the Variables to the Maximum Stress

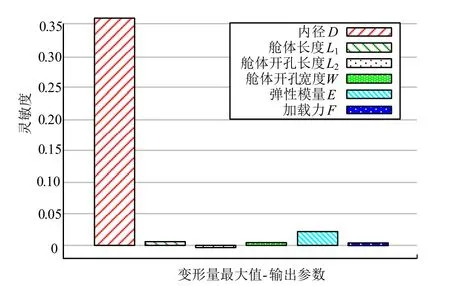
图6 输入变量对最大变形量的灵敏度变化Fig.6 Sensitivity of the Variables to the Maximum Deformation

为了清晰直观地分析舱体结构灵敏度，图5 和图6中相应的灵敏度数值如表5 所示。

由图5、图6 及表5 可知，舱体结构最大应力和最大变形量对内径X 的变化最为敏感，而且随着内径X的减小，最大应力和最大变形均会减小。同理，以上两个输出变量会随着舱体长度、弹性模量和外载的增加而逐渐增大。通过灵敏度值的大小可知，6 个输入变量对 2 个输出变量影响程度的排序均为X>E>Y1>H>Y2>F。

3.4 舱体结构可靠性分析

通过Six Sigma Analysis 模块，可以计算出舱体结构输出变量的累计分布函数，根据该累计分布函数可以获得任意样本点对应的概率值。本文采用LHS 方法生成100 000 个样本点获得最大应力和最大变形量的累计分布函数，分别如图7 和图8 所示。

图7 最大应力累计分布函数Fig.7 Cumulative Distribution Function of Maximum Stress

图8 最大变形累计分布函数Fig.8 Cumulative Distribution Function of Maximum Deformation

由图7 及图8 可以看出，两个输出变量柱状图无较大的间隙或跳跃，说明100 000 次模拟已经足够，且柱状图分布情况较好。在Six Sigma Analysis 中，有两种获得失效概率的方法：一种是通过累计分布函数，通过该函数可以检测产品是否满足可靠性要求，根据图中的黑色样本点拟合出输出变量的累计分布函数曲线，曲线上的每一点的值表示的是输出变量小于该点的概率；另一种方法是从参数概率列表中获得概率值。在参数列表中直接输入某一固定数值，其后显示出的概率值是输出变量小于该固定数值的概率，这种方法得到的概率值更为准确。分别在最大应力和最大变形量参数概率列表中输入最大许用应力358 MPa 以及最大允许变形量0.285 mm，得到相应的概率值，如表6、表7 所示。

表6 最大应力概率Tab.6 Probability List of the Maximum Stress

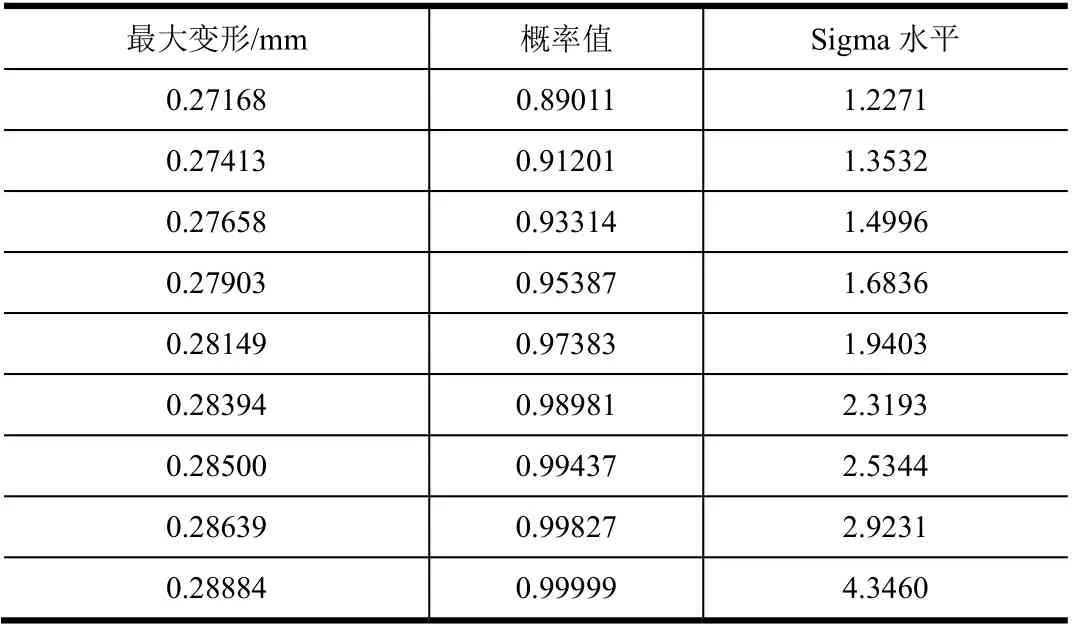
表7 最大变形量概率Tab.7 Probability List of the Maximum Deformation

由表6 和表7 可知，在最大许用应力确定时，该舱体结构的强度可靠度为0.976 86，而在最大允许变形量确定时，该舱体结构的刚度可靠度为0.994 37。因此，在允许值确定的情况下，以该舱体结构的强度作为衡量其可靠性的依据更加保守。

4 结 论

本文采用ANSYS Workbench 对导弹舱体结构参数化建模后，分析了其可靠性以及参数灵敏度，通过研究可知：

a）与Kriging 方法相比，采用AR-Kriging 方法可以提高响应面的全局拟合能力，尤其是在以最大应力为单输出变量时的全局拟合能力；

b）舱体结构最大应力和最大变形量对内径的变化最为敏感，而弹性模量、舱体长度、开孔宽度、开孔长度和外载荷对以上两个输出变量的影响程度逐渐递减；

c）在最大应力和最大应变的允许值确定的情况下，以该舱体结构的强度作为衡量其可靠性的依据显得更加保守。