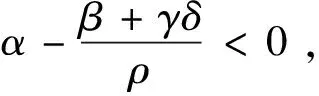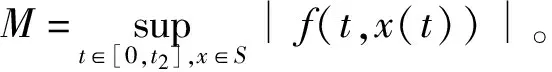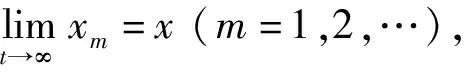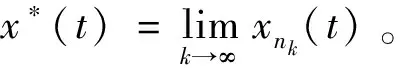Katugampola分数阶微分方程解的吸引性
陈星汝, 顾海波, 王星昭, 陈奕如, 马丽娜
(新疆师范大学 数学科学学院, 新疆 乌鲁木齐 830017)
由于分数阶微分方程比整数阶微分方程更具一般性, 且较整数阶微分方程能更准确地描述客观规律和事物的本质, 因此分数阶微积分在许多领域得到应用,引起了越来越多的关注, 如分数动力学模型、分数控制系统、分数种群动力学模型和分数流体力学都涉及分数阶导数。另外分数阶微分方程也极大地丰富了数学理论的内容, 并渗透到了自然科学的很多领域中。近年来提出的Katugampola分数阶导数, 是对分数阶导数的推广, 具有很大的研究潜能。许多研究者都致力于分数阶微积分的研究,如脉冲微分方程[1]、模糊微分方程等[2-3]。现在基础数学研究和工程应用研究中最常采用的分数阶微积分定义有Riemann-Liouville微积分定义、Caputo微分定义、Grunwald-Letnikov 微分定义等[4]。
2011年, Katugampola[5]将Riemann-Liouville分数积分和Hadamard分数积分推广到同一个形式, 提出了一种推广的分数积分定义, 并于2014年提出了对应的分数导数定义[6], 后命名为Katugampola分数阶导数。随后, Katugampola[7]研究了一类Katugampola分数阶微分方程在初值条件下解的存在、唯一性。此外, 许多学者也研究了Katugampola分数阶算子的性质,如扩展公式[8]、变分法应用[9-12]、控制理论应用[13]、凸性和积分不等式[14-15]以及新算子和类似算子的Hermite-Hadamard类[16-17]不等式等。除此之外,Katugampola 分数导数还应用于物理[18]、动力系统[19-20]、生物学[21]等领域。根据目前文献报道,还没有关于Katugampola分数阶微分方程解的吸引性研究,而吸引性可以为研究其他类型的非线性积分方程解的局部和全局吸引性提供帮助, 方便证明解的稳定性、存在性。
本文将讨论Katugampola分数阶微分方程解的吸引性,如式(1)所示。
(1)
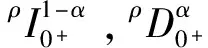
本文利用Schauder不动点定理和非紧性测度方法, 建立了解全局吸引的充分判据, 得到了Katugampola分数微分方程解的吸引性结果。本文结果从本质上揭示了Katugampola分数阶微分方程解的特性。
1 背景知识
C表示所有连续函数x:[0,∞)→X的Banach空间, 范数可表示为式(2)。
(2)
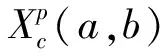
(3)
定义1[6]当-∞ (4) 定义2[7]当0≤a (5) 命题1[22]如果a>0,b>0, 则 (6) 定理1[23]即Schauder 不动点定理,令X为Banach空间,Q为X中的非空有界闭凸子集且Λ:Q→Q为连续的紧映射。则Λ在Q中至少有一个不动点。 定理2[24]即Arzela-Ascoli 定理,为使F⊂C(M)为一个列紧集, 必须且仅须F是一致有界且等度连续的函数族。 对∀{xn}⊆C0([t0,+∞),X)为基本列, 即‖xn-xm‖∞→0,n,m→∞。 对∀ε>0, ∃N>0, 当n,m≥N时, 有 (7) 则对每一个t∈[t0,+∞)有‖xn(t)-xm(t)‖<ε,则{xn(t)}为X中的基本列, 所以{xn(t)}收敛, 记为xn(t)→x0(t),n→∞, 且 即x0∈C0([t0,+∞),X)。 在式(7)中, 令m→+∞, 则 因此xn一致收敛于x0。 我们还需要下面的广义Ascoli-Arzela定理。 引理2[25]当且仅当下列条件成立,集合H⊂C0([t0,+∞),X)是相对紧的。 (1)对任意的T>0,H中的函数在[0,T]上是等度连续的; (2)对任意的t∈[0,∞),H(t)={x(t):x∈H}在X中是相对紧的; (3)如果x∈H,当t→∞时, ∣x(t)∣一致收敛于0。 引理3假设算子f:[0,∞)×X→X是连续的。则式(1)的解可表示为 (8) 且右侧在(0,∞)上是逐点定义的。 我们给出下面的假设: (H1)若t∈(0,∞),x∈X, 则|f(t,x(t))|≤Lt-β|x|δ, 其中L≥0,α<β<1,δ∈。 (H2)存在一个常数κ>0使得对任何有界集合E⊂X,有σ(f(t,E))≤κσ(E),其中σ是非紧的Hausdorff测度。 对任意的x∈C([0,∞),X)和给定的n∈+, 定义算子U (9) 由于0<α<β<1, 我们令γ>0足够小, 使得 令T>0足够大, 使得 (10) 定义集合S S={x(t)|x∈C([0,∞),X), |tγx(t)|≤1,t≥T}, 明显地,S≠∅, 且S是C0([t0,+∞),X)的一个有界闭凸子集。 引理4假设H1成立, 则{Ux:x∈S}是等度连续的且若x∈S, 则 对任意的x∈S, 和t1,t2≥T, 我们有 |(Ux)(t2)-(Ux)(t1)| 进一步, 当0≤t1 相似地,对任意的t1 |(Ux)(t2)-(Ux)(t1)|≤|(Ux)(t2)-(Ux)(T1)|+|(Ux)(T1)-(Ux)(t1)|→0,t2→t1。 因此, 结合上面的论证, 很明显, {Ux:x∈S}是等度连续的。 还需证明若x∈S, 当t→∞时, |(Ux)(t)|是否一致收敛于0。事实上, 我们有 (11) 这证明了若x∈S, 当t→∞时, |(Ux)(t)|一致收敛于0。 引理5假设H1成立。则U为S到S的映射且U在S上连续。 证明 步骤1U:S→S 若x∈S, 通过引理4, 我们有Ux∈C([0,∞),X)。另一方面, 当t≥T时, 运用不等式(10), 我们有 这意味着U:S→S。 则, 当t>T2时 当0 因此, 当m→∞时, 有‖(Uxm)(t)-(Ux)(t)‖→0, 这意味着算子U是连续的。 定理6假设H1和H2成立。则问题(1)有至少一个吸引解。 证明通过引理5可得U:S→S有界且连续。下面将证明U∈C0([t0,+∞),X)是相对紧的。 由引理4可得{Ux:x∈S}是等度连续及若x∈S, 当t→∞时, |(Ux)(t)|一致收敛于0。下面参考文献[26]中的定理4.34的证明方式, 我们由假设H2可得在X中,对任意t∈[0,∞),{Ux:x∈S}是相对紧的。因此, 运用Schauder不动点定理, 算子U有一个不动点xn∈S, 且当t→∞时, 有xn(t)→0。通过使用与引理4相似的证明方法, 可得在[0,∞)上, {xn(t)}是一致有界且等度连续的, 对任意的t∈[0,∞), {xn(t)}是相对紧的。因此, 运用Arzela-Ascoli定理, {xnk}是{xn(t)}的一个一致收敛子序列。进一步我们有, {xnk}满足 (12) 这意味着x*(t)是式(1)的一个吸引解。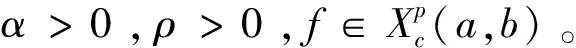

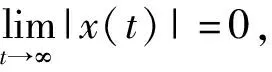
2 主要结果