基于空间认知和社区识别理论的路径选择模型

刘喜敏，徐宁，卢守峰*

(1.南京信息职业技术学院 智能交通学院，江苏 南京 210023；2.长沙理工大学 交通运输工程学院，湖南 长沙 410114)

传统的路径选择模型对出行者的认知能力、对路网交通状况的获取能力、选择偏好等做出了相应的假设。典型的例子是Wardrop原理[1]，假设出行者完全理性，每个出行者的行为是相同的，出行者熟知路网的交通状态。但是大量的证据表明，出行者在城市环境中的路径选择是复杂的认知过程，这个过程有较大的不确定性。近年来，路径选择过程中的不确定性建模被越来越多的学者关注，主要研究内容包括出行者的有限理性、启发式决策。Di等[2]采用随机效用和半补偿模型对有限理性路径选择行为模型进行了研究。Yang等[3]基于确定出行时间的参考点，提出了一种基于累积前景理论的路径选择模型和随机用户均衡模型。龙雪琴等[4]采用决策场理论研究出行者路径选择时的动态过程。刘诗序等[5]以最早到达时间和工作开始时间作为参考点，建立了基于前景理论的双参考点路径选择模型。Papola等[6]提出了一种基于随机效用组合模型的路径选择模型。Lindsey等[7]研究了拥挤的出行条件和出行前所掌握的交通信息对路线选择的影响。Li等[8]提出了利用社区识别生成锚点的数据驱动方法分析路径选择。Alizadeh等[9]强调要同时考虑路线特性和锚点，从而提升路径选择模型的估计和预测能力。Manley等[10]利用智能体研究了个体的空间认知差异对路径选择的影响。

总体上，现有的路径选择方法采用的理论包括前景理论、期望效用理论、离散选择模型、博弈理论、随机效用和半补偿模型以及随机效用组合模型等，这些模型假设出行者是完全理性或有限理性的，其特点是追求效用最大化或阻抗最小化，没有考虑城市路网的空间结构，因此与人们的实际路径选择存在偏差，导致规划的路网结构与人们对路网的使用不相匹配。

本文将启发式路径选择模型与模块增益算法相结合，用社区识别理论揭示驾驶员的路径选择与路网结构的关系，采用模块化信息解析路网结构，划分交通出行大区，并设计相应的路径选择算法。

1 集成空间认知和模块增益的路径选择模型

空间认知机制将路径选择划分为三个层次：社区选择层次、节点选择层次和道路选择层次[11]。在社区选择层次中，本文采用模块增益算法，利用静态权重(距离)和动态权重(速度)实现社区划分，根据社区内包含的路段数量选择合适的划分结果，划分结果的选择主要凭借经验，即包含的路段数量不能太多或太少，具有一定的规模和代表性。然后利用社区消除法(elimination by aspects，EBA)与最佳社区选择法(take the best，TTB)确定最佳社区。节点和路径选择两个层次采用Dijkstra最短路径算法。

模块增益量计算[12]如公式(1)所示。

(1)

其中，∑in是社区C内链接权重总和，∑tot是社区C中与节点相连的链接权重之和，ki是复杂网络中与节点i链接的权重总和，ki,in是社区C中节点i与潜在节点的链路的权重之和，m是复杂网络中链接权重之和。

模块化增益算法的核心是通过计算模块化增益量形成递阶的社区结构。初始化时，将路网中每一个节点(交叉口)作为一个社区。当一个节点移入到新的社区比保留在当前社区具有更大的模块化增益量时，就将其移入新的社区，否则保留在当前社区。这个过程循环一次就形成一级结构，在此基础上重复该过程可以形成多级递阶结构，至每一个节点到相邻社区的模块增益值ΔQ均不大于0为止。社区划分的数量和大小需根据实际路网的空间结构来确定。

采用EBA和TTB选择最佳社区。其中EBA可减少备选社区的数量，距离最大或偏差角度最大的备选社区被消除。TTB利用表1中4种属性对途经社区进行比选，利用这4种属性对本研究收集的数据进行分析。调查数据包括OD问卷调查数据(静态)、出租车GPS数据(动态)。然后以地理信息系统(geographic information system，GIS)为平台，将出行者的出行起终点和所选路径进行标注，利用路径选择的结果进行反推，得出属性的重要度从大到小排序为偏差角度最小、最短用时、最快速度、最短距离。根据属性依次进行对比，直至剩下唯一的备选社区。在评估过程中，若两个或多个备选社区结果一致，则进行随机选择。

表1 属性判定表

利用Matlab软件对模块增益算法和最佳社区选择规则进行编程，实现骨架道路识别。边是节点(交叉口)的物理连接(路段)，可通过路段距离和路段速度这两种属性值进行度量。距离或速度相近的多个节点可聚类为一个社区，社区即为节点的集合，即属性特征相近的区域路网。若一条道路的多条路段均被识别为社区间连接路段，则该条道路被称为骨架道路。模型首先在骨架道路中选择，然后在区内道路选择。具体步骤如下：

(1)首先对划分路网的节点进行标号，将长沙市中心城区路网每个交叉口按顺序依次标号，共927个节点；其次将两节点间路段进行标号，共1580条路段。

(2)建立属性矩阵。创建927×927的属性矩阵。距离(速度)矩阵是将两节点路段间距离(速度)填入，若两节点不相连则为0。

(3)基于距离权重的静态属性代入社区识别的无向型算法，基于速度权重的动态属性代入有向型算法，得出分区结果。

2 算例

2.1 基于静态路阻的路径选择结果验证

以长沙市中心城区路网(图1中环线内的路网)为例，对其依据路段距离进行划分，共得到了5个划分层次，社区数量分别是第一级划分274个、第二级划分127个、第三级划分56个、第四级划分10个、第五级划分1个。根据社区面积和包含的路段数量，将第三级(如图2(b)所示)和第四级(如图2(a)所示)划分结果作为出行者对长沙市路网的空间认知结果，进行对比，图2中的绿短线表示识别出来的连接各大区之间的主要路段。

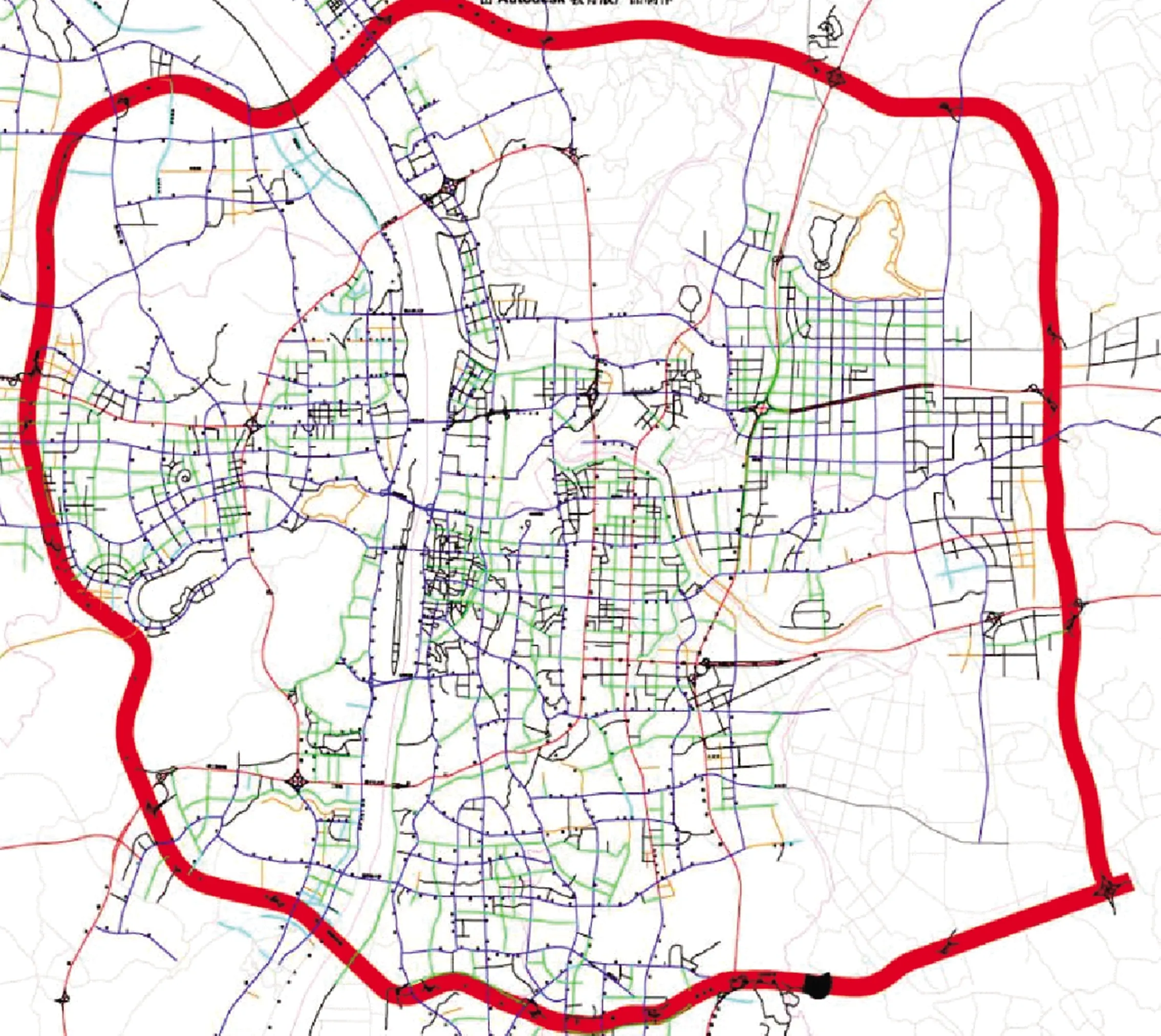
图1 长沙市现状路网

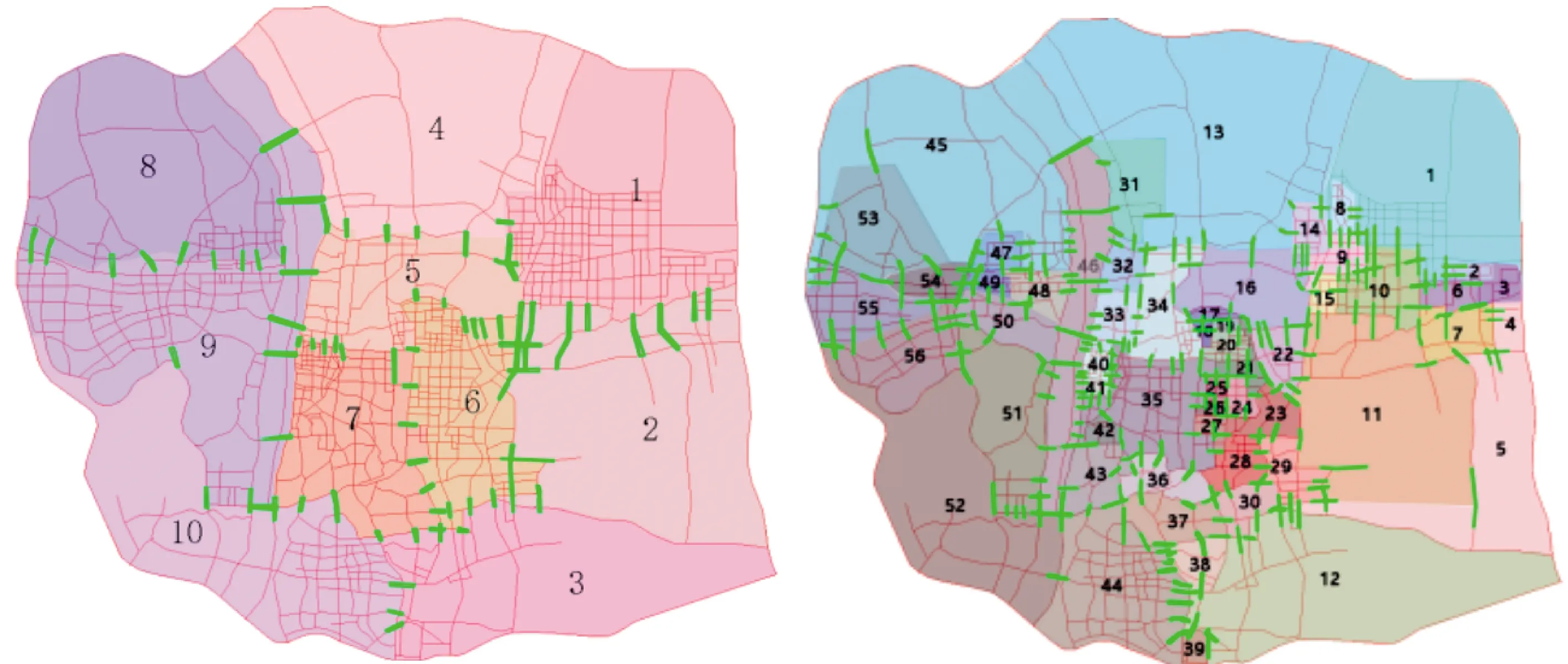
(a)第四级划分结果 (b)第三级划分结果

第四级划分结果为10个大区，如图2(a)所示。以社区1至8的跨区出行为例，利用本文提出的路径选择模型得出最佳社区。

(1)首先识别社区1的相邻社区为社区2、4和5，根据EBA消除理论，以“与目标社区距离”为依据，消除社区2。接着进行TTB选择，依次对比表1中属性。社区4与5的“与目标社区偏差角度”指标值接近，均可作为备选社区。“最短距离”“最快速度”“最短时间”3个指标对比，社区4至8跨区出行的主要路径为北二环与福元路大桥，承担社区5至8跨区出行的主要路径为三一大道(岳麓大道)，两组道路均属于过江通道，道路等级均为长沙市主干道，指标值接近，因此社区4与5均为最佳社区。

(2)节点与路径选择。若选择社区5作为最佳社区，连接大区的路径为社区1—5—9—8。社区1至5仅有三一大道相连，所以最佳路径为三一大道；社区5与9之间相连路段为银盆岭大桥与营盘路隧道，根据最短路径法，以及与目标社区8的最小偏差角度法，最佳选择路径为三一大道(含银盆岭大桥)；社区9与8共11条路径相连，且道路等级全部为快速路与城市主干道，具体的路径选择要根据目的地的位置采用最短路径法确定。若选择社区4作为最佳社区，连接大区的路径为社区1—4—9—8。社区1与4仅有开元路相连，最佳路径为开元路；社区4与9相连路段为北二环、福元路，北二环因与社区8距离较长，因此最佳路径为开元路；社区9至8的最佳路径要根据目的地的位置采用最短路算法确定。因此社区1至8的最佳路径为三一大道(含银盆岭大桥)开元路。

为验证提出的路径选择算法的准确性，采用长沙市需要从社区1至8跨区出行的上班族出行调查问卷的数据进行检验。调查内容包括出行方式、出行时间、出行过程中经过的路径顺序等。挑选20份起始社区为1，终止社区为8的出行问卷，路径选择比例如表2所示。

表2 市民实际路径选择

从表2可知，社区1至8的跨区出行，实际出行路线主要聚集在开元路与三一大道(含银盆岭大桥)，两条路段被实际选择概率合计为85%。因此，认为建立的路径选择模型具有较好的合理性和较高的真实性。

2.2 基于动态路阻的路径选择结果验证

图1中的路网以路段的速度为权重，分别采用高峰时段速度、平峰时段速度进行计算，基于动态路阻的划分结果对于动态交通管理更有指导意义。

2.2.1 采用高峰时段速度属性划分

采用高峰时段速度，共得到5个划分层次，社区数量分别为第一级划分292个、第二级划分134个、第三级划分46个、第四级划分12个、第五级划分1个。将三级和四级划分结果作为出行者对长沙市路网的空间认知结果，见图3。与基于静态路阻的第四级划分对比，发现南北向承担跨区出行的路径发生改变。在距离属性划分中，南北向连接路段主要分布在岳麓大道、远大路、南二环、香樟路，而在高峰时段速度属性划分中，南北向连接道路为开元路与香樟路。这种区别表明了交通状况对道路使用的影响。两次划分中识别出的跨区出行路段基本一致，且东西向连接道路一致，主要集中在过江通道。对第四级划分应用提出的算法，以社区1至11为例，得到最佳路径为开元路—芙蓉路—银盆岭大桥、开元路—芙蓉路—营盘路或开元路—北二环。

对第三级划分，与基于静态路阻第三级划分对比。两者不同点在于本次划分结果为46个社区，相比基于静态路阻的划分减少了10个社区，且划分的社区位置与面积大小不同。图2中的7个社区(21、23～28)在图3(b)中仅划分为一个社区。该结果说明，基于距离划分的该7个社区在高峰时段内车辆行驶速度相近。两者相同点在于承担跨区出行的路径一致，包括二环线、万家丽路、芙蓉路、过江通道、三一大道、开元路等。

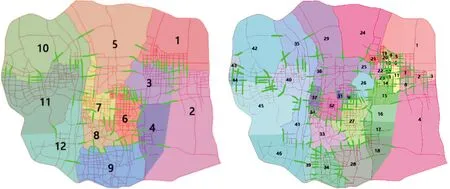
(a)第四级划分结果 (b)第三级划分结果

2.2.2 采用平峰时段速度属性划分

采用平峰时段速度，共得到了5个层次划分，第四级和第三级划分如图4所示。

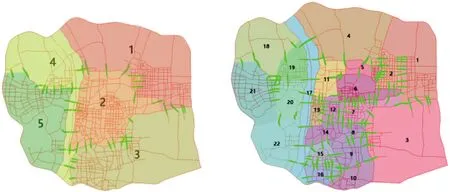
(a)第四级划分结果 (b)第三级划分结果

对比基于高峰时段速度与基于静态路阻的第四级划分结果发现，平峰时段速度划分的社区数量较少，说明在平峰时段各路段速度值较接近；与平峰时段不同，在早晚高峰时段，承担跨区出行的主要路径会产生交通拥堵，行驶速度较小，因此基于不同属性的划分结果差异较大。

与基于高峰时段速度属性的第三级划分结果对比，采用平峰时段速度属性的第三级划分结果为22个社区，比高峰时段减少了24个，且划分社区位置与面积发生较大改变。该情况说明两个时段社区间的速度发生较大变化，尤其发生在跨区出行的主要路径，这些路径在高峰期间交通拥堵，速度较小；而在平峰期间，车流量小，且道路等级均高于城市主干道，速度较大。两者相同点在于承担跨区出行的路径基本一致。

为了分析交通拥堵对出行者路径选择的影响，从长沙市出租车监控中心收集了出租车GPS数据进行验证。收集内容为每辆出租车一天内GPS数据，包括车辆ID、经纬度、车辆当前速度、当前时间、载客状态等信息。6:00—9:00与17:00—20:00作为高峰时段，其余为平峰时段，提取一天内每辆出租车每一单载客路径。

共收集了4辆出租车一天内的载客路径共224条GPS数据，其中高峰时段88条，有12条的起终点位于社区1和11；在平峰时段的载客路径共136条，有18条的起终点位于社区1和5。具体路径选择情况如表3所示。

表3 出租车实际路径选择

由算法得到，在高峰时段，社区1—11的最佳路径为开元路—北二环、开元路—芙蓉路—营盘路、三一大道(含银盆岭大桥)，在表3中，这三条路径在实际出行过程中被选择的比例合计为75%。在平峰时段，社区1至社区5的最佳路径为开元路—潇湘路、开元路—银杉路、远大路—东二环—南二环，在表3中，这三条路径在实际出行过程中被选择的比例合计为73%。因此认为本文所建立的路径选择模型具有较好的合理性和较高的真实性。

3 结论

本文把启发式决策、空间认知以及社区识别理论相结合，提出了基于路网结构的路径选择模型，并给出了算法步骤，假设出行者先对大区进行选择，然后再利用最短路径原则选择区内的道路。分别用静态路阻(距离)、动态路阻(速度)对长沙市中心城区路网进行解构，计算路径选择集，结果表明识别的大区之间的道路与长沙市现状路网的等级结构相符。采用问卷调查方法和出租车GPS数据对实际的路径选择轨迹进行提取，并将理论计算结果与实际调查结果进行对比分析，一致率在73%以上，因此认为本文所建立的路径选择模型具有较好的合理性和较高的真实性。下一步可结合路网流量数据，分析识别出来的社区连接路径上的流量与社区内道路流量之间的关系，进一步研究空间认知对出行者路径选择的影响。