基于伺服液压缸往复运动的Y形密封圈结构参数优化①

雷雨念 陈奎生 湛从昌

(1:武汉科技大学冶金装备及其控制教育部重点实验室 湖北武汉 430081；2:武汉科技大学机械自动化学院 湖北武汉 430081)

1 前言

作为液压伺服系统中的一个执行元件，伺服液压缸的性能直接关系着伺服系统运行的精度。液压伺服系统对稳定性、精度和快速响应性上有着极高的要求[1]。因此，伺服缸的密封与泄漏的研究就显得极为重要。Y型密封圈是液压与气动系统中常用的往复密封件之一。其具有结构简单、使用寿命长、耐压性好、可靠性高等优点。对Y型密封圈的研究大多都是采用了有限元分析模型。汝绍锋等[2]分析了在初始压缩率不同的情况下，Y型密封圈密封性能的变化规律。李腾等[3]探讨了密封圈的唇外倾角以及唇谷高给密封圈密封性能带来的影响。孟华荣等[4]分析了Y型密封圈在工作温度、流体压力等不同的情况下，最大剪切应力的位置和大小的变化。王刚等[5]研究分析了在压缩率和载荷不同的情况下，Y型密封圈应力随油压的变化情况。Zhang Yajun等[6]分析了Y型密封圈在温度和工作压力不同的情况下，密封圈密封性能的变化。黄乐等[7]分析了Y型圈抗挤出能力随工作压力的变化情况。王世强等[8]分析了在不同的工作压力下，密封圈的变形与压力分布情况，并通过分析得出了密封圈接触应力的分布规律。

Y形密封圈截面形状复杂，不同的尺寸参数会直接影响密封圈的密封性能和使用寿命。目前，Y型密封圈的截面设计很难有统一的标准，很大程度上都依赖于设计师平时的工作积累[9]～[11]。本文在之前研究的基础上对密封圈内外唇高度差和密封圈的唇厚度进行研究，利用ANSYS有限元分析软件，模拟Y形密封圈的唇高度差和唇厚度在不同油压下的应力和压力分布情况，并分析不同的结构参数对密封圈密封性能的影响。

2 伺服液压缸结构及其工作原理

液压伺服系统是使位移、速度或力等能自动准确地随着输出量的变化而发生变化，而伺服液压缸作为液压伺服系统的执行元件，能够实现系统机械能输出，可以在高频环境下驱动工作载荷，从而实现高精度、高响应控制，其性能的好坏直接影响着系统的控制精度。

图1 伺服液压缸结构图1-活塞杆;2-防尘圈;3-前端盖;4-Y型密封圈;5-支撑圈;6-缸体;7-螺母;8-连杆;9-套筒;10-安装板;11-位移传感器;12-位移传感器支座;13-后端盖

所选伺服液压缸结构如图1所示。图1中，液压缸通过液压油产生的压力进行往复运动时，防尘圈与外部空气侧相通，防止灰尘混入液压缸的往复密封件中，导致活塞杆磨损；Y型圈作为密封件可以防止发生内泄露；支撑环起到支撑作用，防止金属之间直接摩擦，保护活塞杆不被损坏。

3 有限元模型的建立

3.1 几何模型结构参数

现以某液压缸活塞杆用Y形密封圈为研究对象，所用密封圈型号为Y50×65×12.5，其材料为腈基丁二烯橡胶(NBR)，主要截面尺寸如图2所示。

图2 Y形密封圈参数化模型(mm)s-唇高度差;e-唇厚

3.2 有限元模型建立

根据密封圈及其相应的沟槽尺寸建立几何模型。活塞杆基本直径为50mm，密封圈安装完成之后，活塞杆和缸盖之间的间隙为0.2mm，密封圈工作压力范围为0～15MPa。活塞杆运动速度为0.1m/s～0.5m/s，端盖与活塞杆之间的间隙为0.2mm。为了便于做有限元分析，现将密封圈材料做出以下考虑：

1)忽略其在运动过程中会发生的松弛和蠕变。

2)将橡胶密封圈的材料抽象为近视不可压缩。

3)将密封圈材料视为各向同性且均匀连续。

4)忽略温度的影响。

现将三维轴对称结构简化为二维轴对称模型，并在施加载荷时使用较小的载荷增量，以此来保证计算收敛。

由于其应力表现为强烈的非线性，本文采用2个系数的Mooney-Rivlin模型[12]来对Y型密封圈材料进行分析。该材料的函数关系式如下：

W=C10(I1-3)+C01(I2-3)

(1)

式中：W-应变势能；

I1、I2-第一和第二Green应变不变量；

它与橡胶硬度H和弹性模量E的关系如下：

lgE=0.0198H-0.5432

(2)

E=6(C10+C01)

(3)

C01=0.25C10

(4)

材料硬度同温度之间的关系为：

H=H0+φ(T-23)

(5)

式中：H-工作温度下材料的硬度;

H0-标准温度23℃时材料的硬度，单位IRHD；

图8为0.125 g TNT炸药球填实爆炸下，花岗岩中实测的球面波径向粒子速度波形的时间特征随比距离的变化关系。可以得到：在测点半径10 mm处，波形上升沿ΔTr约为0.5 μs；在测点半径120 mm处，ΔTr约为5.3 μs；二者相比，ΔTr展宽了约10倍。另外，ΔTr、波形半高宽ΔT1/2及波形正向脉宽ΔT+均有随着比距离增加而增加的趋势。球面波在花岗岩中传播的展宽效应也反映了其非线性动力学响应的复杂性，基于理想弹性假设的波传播理论，无法对其波形的传播演化规律进行合理解释。

φ-修正系数；

T-工作温度，单位℃。

本文取修正系数φ取值为0.175，伺服液压缸工作温度T为23℃，标准温度下硬度H0为85IRHD。经计算得到弹性模量E=14.44MPa，C10=1.87,C01=0.47。

做有限元分析时使用了两个载荷步，先让活塞杆移动到标准的位置，使其和端盖之间的间隙为0.2mm，使密封圈处于压缩状态，然后施加流体压力，活塞杆向前移动。为了避免Y型密封圈唇边和密封圈之间接触对的互相渗透，这里采用的求解方法为Lagrange法。当P=0MPa时，通过活塞杆的轴向移动得到Y型密封圈的初始有限元模型，情况如图3所示，箭头所指方向为活塞杆移动方向。

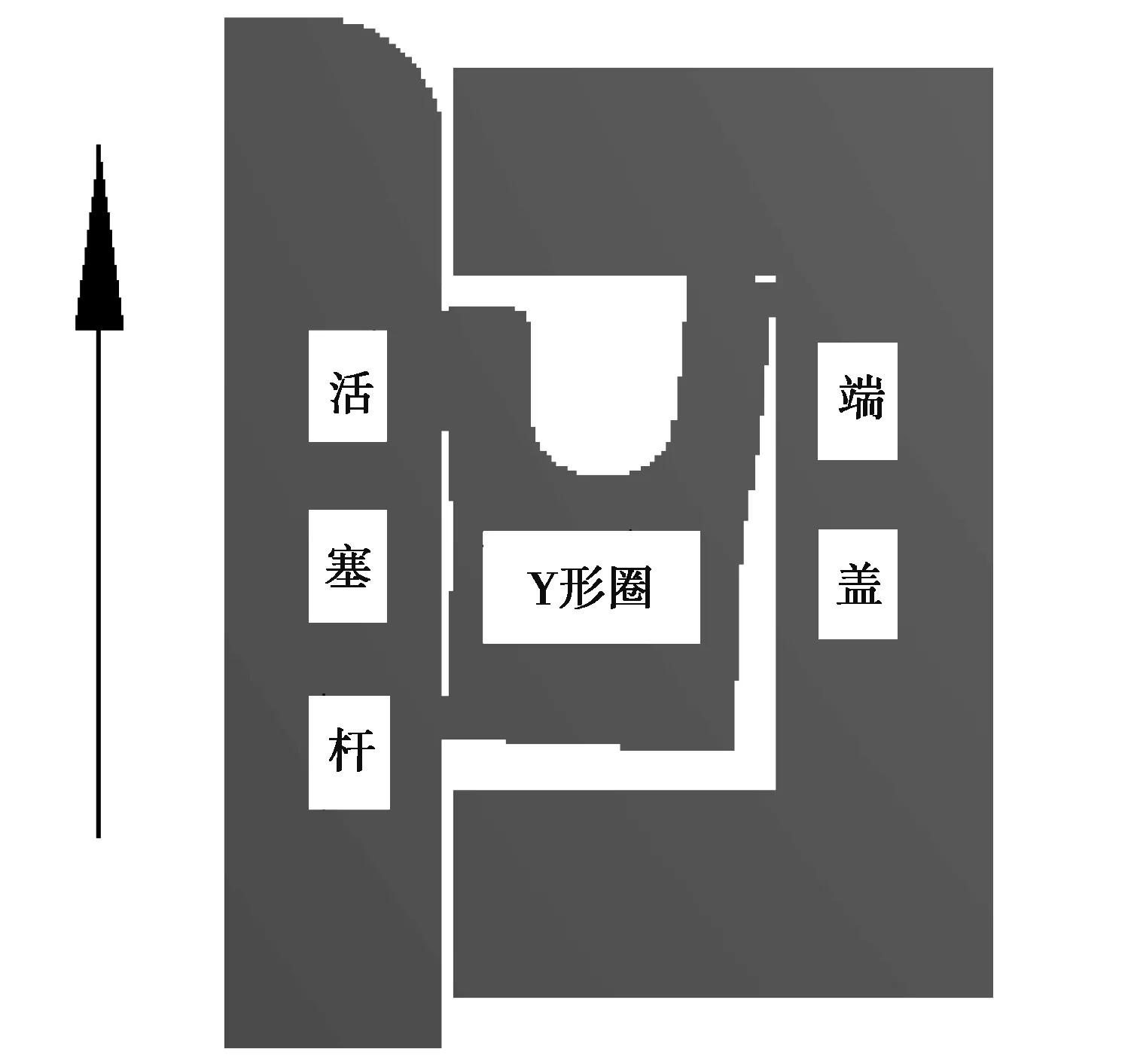
图3 Y形密封圈轴向移动模型

4 计算结果与分析

4.1 对密封圈密封性能的影响

4.1.1 接触压力

利用ANSYS软件对Y形圈模型进行模拟仿真，通过改变Y形圈的唇高度差s和油压p，得到相应情况下的Von Mises应力云图和接触压力云图，并以此为依据，分析唇高度差对密封圈密封性能的影响。Von Mises应力即等效应力，反映了截面上的主应力差值的大小。Von Mises应力值越大的区域，材料越容易出现松弛，寿命越短，接触应力的大小则直接反映了密封圈的密封性能。当最大接触压力不小于油压p的时候，Y形密封圈才能保证其密封效果，接触压力越大，其密封性能越好。

当油压为P=3MPa时，密封圈唇厚度e为2mm，摩擦系数f=0.2时，改变Y型密封圈内外唇高度差，密封圈与活塞杆的接触压力和与端盖的接触压力情况如图4所示。

由图4可以看到密封圈的最大接触压力总是大于油压的，而且唇高度差对于短唇接触压力的影响较大，对于长唇的接触压力没有明显影响。并且随着唇高度差s的增大，密封圈的最大接触压力呈先增大再减小的趋势，当s=1.25mm左右时，短唇唇接触压力达到最大值，之后呈现下降趋势，当s的值大于2.25mm之后，模型不收敛。

图4 内外唇最大接触压力

当流体压力为3MPa，密封圈唇厚度e为2mm，摩擦系数f=0.2，唇高度差s取不同值时，Y密封圈两边唇的压力分布图如图5所示。红色区域为压力大于3MPa的区域，即有效密封区域。

由图5可看出，随Y型密封圈唇高度差s变大，有效密封区域的长度也在随之变短,综合两图分析可知当s的值在0～1.25mm之间时，Y密封圈密封性能更好一些。

4.1.2 Y形密封圈应力分析

当摩擦系数取f=0.2，Y形密封圈唇高度差为1mm，密封圈唇厚度取2mm时，流体压力P取分别取P=2MPa,P=4MPa,P=6MPa，此时密封圈应力云图如图6所示。

图5 密封圈接触压力云图

图6 最大Von Mises分布情况

图6可得，在不同流体压力的情况下，Y型密封圈应力集中部位都是在唇谷的位置，现对不同s值的Y形密封圈分别进行分析，观察其最大Von Mises应力的变化情况并对其密封性能指数β进行计算，变化情况如图7、图8所示。

图7 最大Von Mises应力随压力变化图

这里有：

β=(pmax-p0)/p0

(6)

式中：β-密封性能指数；

pmax-密封圈最大接触压力，单位MPa；

p0-所施静态油压，单位MPa。

综合图7图8分析可得，取不同s值时密封圈最大Von Mises应力值如图7所示。可以知道，最大Von Mises应力值随静态油压的增大而增大，油压较小时，五条曲线趋近重合，当油压逐渐增大时，随s值变大，密封圈最大Von Mises应力值有所减小。由图8可得，随着Y形密封圈油压增大，密封性能指数β在逐渐减小，即密封圈的工作油压有一个最合适的范围，过高的油压会使得密封圈的密封性能降低。

图8 s不同时密封性能指数β

4.2 密封圈唇厚度e对密封圈密封性能的影响

当Y形密封圈摩擦系数为0.2，唇高度差s为1mm摩擦系数f=0.2时，唇厚度分别取e=2mm，e=2.5mm和e=3mm，其最大接触压力随油压变化情况为图9所示。

图9 不同厚度时最大压力变化曲线

最大接触压力随油压变大而变大，近似呈线性关系，当唇厚度变大时，密封圈最大接触压力略有上升，但其变化并不明显，在e=1.5mm时，模型不收敛。在该条件下对密封圈最大Von Mises应力进行分析，得到应力随油压变化的图，如图10所示。

图10 不同厚度时最大Von Mises应力变化曲线

综合可以看出随着唇厚度e的增加，Y形密封圈最大Von Mises应力在变大，密封圈容易出现松弛，使得密封圈寿命变短。

4.3 不同的摩擦系数对密封圈性能的影响

当Y型密封圈唇高度差s为1mm，唇厚度e为2mm时，摩擦系数f取值分别为0.1、0.15、0.2，对其最大Von Mises应力进行分析，研究两者之间的变化关系，变化曲线如图11所示。

图11 不同摩擦系数时最大Von Mises应力变化曲线

由图11可以看出，当压力P比较小时，不同摩擦系数对其最大Von Mises应力的影响并不大，但随着压力P变大摩擦系数对最大Von Mises应力的影响变大，且摩擦系数f越小，最大Von Mises应力越小。

5 结论

1)当Y形密封圈的唇高度差有所增加时，密封圈的最大接触压力会有所上升，当s大于1.25mm时开始呈现下降趋势。

2)随着其s的值变小，Y型密封圈在接触压力有所上升的同时有效密封区域会随之减小，该现象在油压较大时更为突出，为此，密封圈s的取值在1～1.25mm时较为合适。

3)密封圈唇厚度过大时会导致密封圈唇谷处应力变大，降低密封圈的使用寿命。

4)若伺服缸的摩擦系数f变大，会导致最大Von Mises应力相应变大，即会使密封圈容易损坏，使密封圈的使用寿命变短。