一道二元最值题的多视角探究

陈常礼

(山东省日照实验高级中学，276800)

二元最值问题,因其注重考查考生的综合思维能力,具有很好的区分功能,能够很好地考查学生的数学思维能力,一直备受高考命题者的青睐.此类问题求解时往往技巧性特别强,学生不易掌握.本文以2020年江苏省高考试题的解法予以探究,供参考.

试题已知5x2y2+y4=1(x,y∈R)，则x2+y2的最小值是______.

这是一道典型的二元最值问题,虽然试题表述简洁,但由于已知条件式的左边是二元四次齐次结构,目标式则是二元二次齐次式,因而求解过程富有挑战性,也给考生的发挥提供了较大的空间.展开联想、注重转换,充分利用基本不等式和导数这些求解最值的工具,是解答该试题的通性通法和有效途径.

视角1基本不等式法

解法1由条件5x2y2+y4=1,得y2(5x2+y2)=1,所以4y2(5x2+y2)=4.

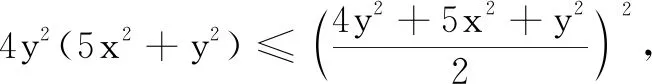
评注“配凑”系数或式子的构成得到应用基本不等式的结构形式,是利用基本不等式求最值的常用技巧,该解法需要有较强的洞察力和配凑能力,还要有整体把握的意识.

分析2由条件,左边提取y2因式分解后,采用双变量换元,代入所求式x2+y2后利用基本不等式解决问题.

解法2由条件5x2y2+y4=1，可得(5x2+y2)y2=1.令5x2+y2=a,y2=b(b>0),则ab=1.

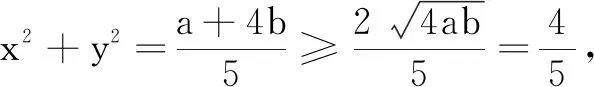
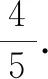
评注该解法通过对条件式因式分解后进行双换元,为直接利用基本不等式求最值创造了条件,避免了解法1“配凑”系数,使求解过程更加简捷.

视角2消元法

解法3消元与基本不等式法

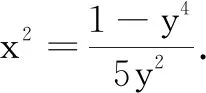
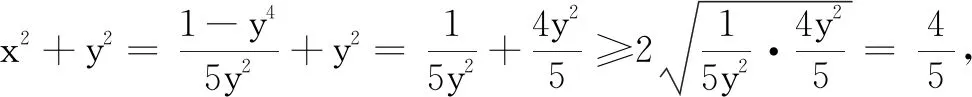
解法4消元与导数法

评注基本不等式法、导数法是求解一元函数最值问题的最基本方法.用基本不等式求最值时,要正确理解和掌握“一正、二定、三相等”的内涵:“一正”是指参数必须为正,“二定”是指和或积为定值,“三相等”指等号要能成立.而大多数一元函数都能利用导数法求解其最值.

视角3三角换元法

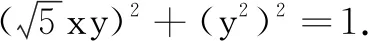
评注该解法由条件式变形后联想到三角函数,利用三角换元对x2+y2变形，再利用基本不等式求得最值,需要丰富的联想能力.

由上可见,对表面上看起来比较繁琐、无从下手的二元最值问题,只要转换视角,巧用联想,挖掘已知式或所求式的特征,便可找到问题解决的切入点.这对我们培养数学抽象和数学建模、数学运算等数学核心素养都有一定的帮助.