采煤机摇臂齿轮传动系统的动态仿真

刘乙慧

(山西焦煤机械电气有限公司， 山西 太原 030024)

0 引言

采煤机作为煤矿开采的重要机械设备，对提高采煤效率和企业经济效益具有重要作用。摇臂齿轮传动系统作为采煤机的核心部件，承担了采煤机80%以上的功率消耗[1-4]，采煤机通过摇臂将动力传递给截割滚筒实现落煤和装煤，其性能直接影响采煤机的可靠性和效率。摇臂传动系统主要由各级齿轮传动组成，由于工作环境恶劣，齿轮系统不仅要受到外部载荷激励的影响，还要受到内部齿轮啮合误差和内部激励的作用，因此系统的负载特性较为复杂。

采煤机摇臂内部齿轮一般都是在静力学的基础上进行设计和计算，随着采煤机设计功率的不断增大，传统设计方法很难满足使用要求，为了提高采煤机摇臂传动系统的可靠性，降低系统发生故障的概率，本文对采煤机摇臂传动系统的动态特性进行了研究。

1 摇臂齿轮传动系统

图1 摇臂传动系统示意图

本文主要研究摇臂传动系统中齿轮的动态响应，忽略系统中轴承、密封等其他零件的影响。

2 传动系统工作参数的计算

2.1 额定负载

采煤机截割部在工作过程中受力较复杂，并且受力的大小不固定。采煤机本体主要受3个力的作用，即采煤机截割阻力、引阻力和侧向力。受煤层特性、滚筒截齿排列方向等因素的影响，3个力的大小和方向均随时间的变化而变化。将截齿所受的负载转换至行星架中心线上后，行星架轴线上受到3个方向力和力矩。考虑到牵引力和侧向力主要对系统中的轴承影响较大[7-8]，本文通过简化后主要考虑截割阻力矩对摇臂齿轮传动系统的影响。

最大恒定负载是采煤机各工况中使用时间最长的工况，并且在该工况状态下，电动机的功率为额定功率。因此，对该工况下系统的动态特性进行研究能够更加准确的了解系统的性能和质量情况。以7LS06-LW536型采煤机进行研究，其摇臂的截割功率为750 kW，摇臂系统总的传动比为56，忽略传动系统效率，摇臂系统最大的输出扭矩为：

(1)

式中：T为摇臂传动系统输出最大扭矩，N·m；P为电动机的输出功率，kW；N为电动机转速，r/min；i为摇臂传动系统总的传动比。

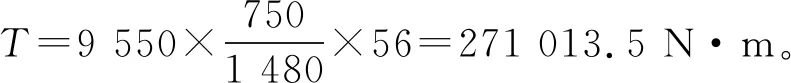
2.2 传动系统啮合频率

齿轮在啮合过程中周期性的进入啮合和退出啮合，将产生周期性的冲击载荷，并且齿轮对工作过程中存在单齿啮合期和双齿啮合区的交替，这些齿轮传动的固有特点使得系统承受交变载荷的影响，交变载荷的作用必将引起齿轮的振动。齿轮啮合的基本频率即啮合频率计算方法如下：

(2)

式中：fm为齿轮的啮合频率，Hz；N1、N2为主动齿轮转速和从动齿轮转速，r/min；Z1、Z2为主动齿轮齿数和从动轮齿数。

从式(2)可以看出，对于定轴齿轮传动，配对的主动齿轮和从动齿轮啮合频率相同。对于2K-H行星轮系，各齿的啮合频率相等，本文通过计算太阳轮的啮合频率来进行分析，其啮合频率为：

fms=(frs-frc)×ZS

(3)

式中：fms为太阳轮的啮合频率，Hz；frs为行星轮系中太阳轮的转动频率，Hz；frc为行星轮系中行星架的转动频率，Hz；ZS为太阳轮的齿数。

从式(3)可以看出，行星轮系的啮合频率与各齿轮的转动频率有关，因此需要对各传动比进行计算。定轴传动中，传动比为：

i1.2=z1/z2

(4)

式中：i1.2为定轴齿轮传动比；z1为主动齿轮的齿数；z2为从动齿轮的齿数。

2K-H型行星轮系传动比为：

i1H=z3/z4+1

(5)

式中：z3为内齿圈齿数；z4为太阳轮齿数。

根据滚筒给出的额定转速26.4 r/min，即摇臂传动系统第二级行星齿轮传动系统中行星架的转速为26.4 r/min，结合上述(2)～(5)式，可以计算出系统各部分的啮合频率如表1所示。

3 仿真模型的建立与分析

3.1 模型的建立

本文在UG装配环境下对齿轮传动系统中各零部件进行组合，然后将系统装配体模型以parasolid格式导出并保存，并在ADAMS/view环境中导入后建立MODEL_1动力学模型。旋转副设置中将机架假设为ground，在8个齿轮质心处设置Joint约束副，并分别添加相对于ground的旋转副约束；在第一级太阳轮、第一、二级行星架的质心处添加相对于ground的旋转副约束；一、二级行星轮系中各行星轮质心处添加相对于行星架的旋转副约束；两行星轮系内齿圈质心处分别添加相对于ground的固定副约束。

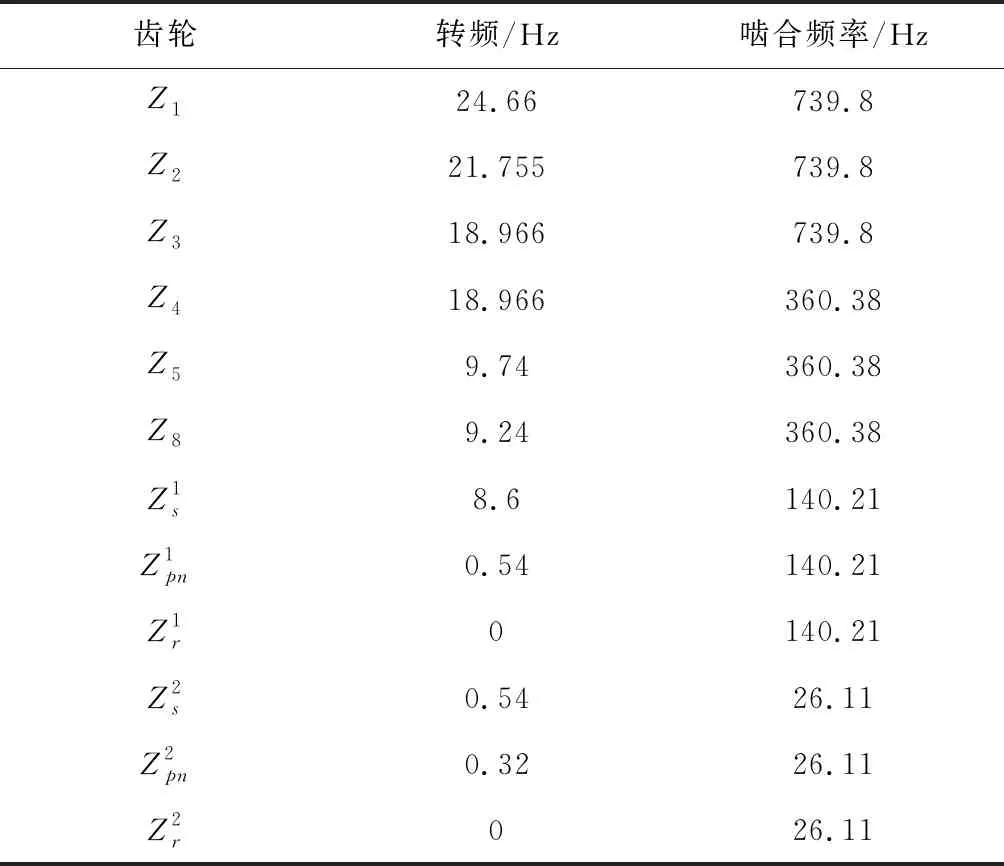
表1 各齿轮的转频和啮合频率

齿轮啮合过程中，应用ADAMS/Solve中碰撞函数接触算法计算出各轮对间的接触力，从而用接触力来模拟各齿轮副的啮合力。考虑齿轮啮合过程中摩擦的影响，分别设置静摩擦因素、动摩擦因素为0.08和0.05，静滑移速度、动滑移速度为0.1 mm/s和1 mm/s，建立了如图2所示的采煤机摇臂传动系统模型。

图2 采煤机摇臂传动系统模型

3.2 动态特性响应分析

采煤机摇臂传动系统变载响应分析对研究传动系统稳定性和可靠性至关重要，通过上述分析，摇臂传动系统受截割阻力产生的扭矩影响较大，因此本文重点研究输入扭振对传递系统的响应情况。考虑到齿轮传递系统零件较多，系统较为复杂，而且系统每一级齿轮传动具有相同的啮合频率，受扭矩激励后响应特点相似，所以重点选择第二级传动中高速齿轮Z4作为仿真分析的研究对象。仿真过程中通过设置不同的滚筒输入载荷，即空载、F=1.35×105N·m、F=2.7×105N·m 3种不同情况进行分析，其中F=2.7×105N·m为滚筒的额定输入载荷。

通过ADAMS中simulation模块对仿真参数进行设置，并分别添加3种不同的载荷，应用GSTIFF求解器进行仿真，在PostProcsser后处理模块中输出齿轮的时域图，将相应数据导出后，在MATLAB中做出3种不同输入情况下时域图和频域图，具体如图3～图5所示。

(a) 时域图

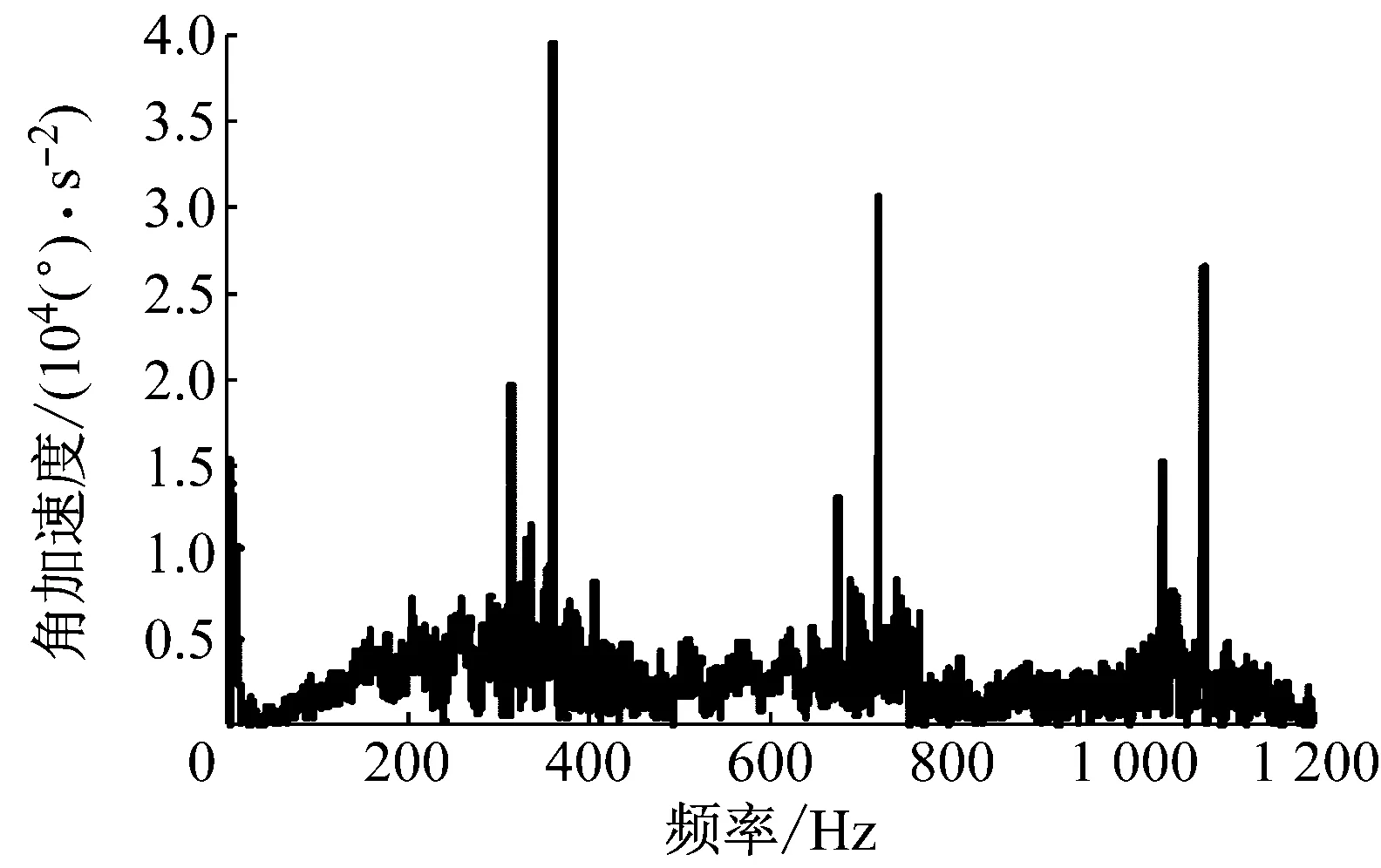
(b) 频域图

(a) 时域图

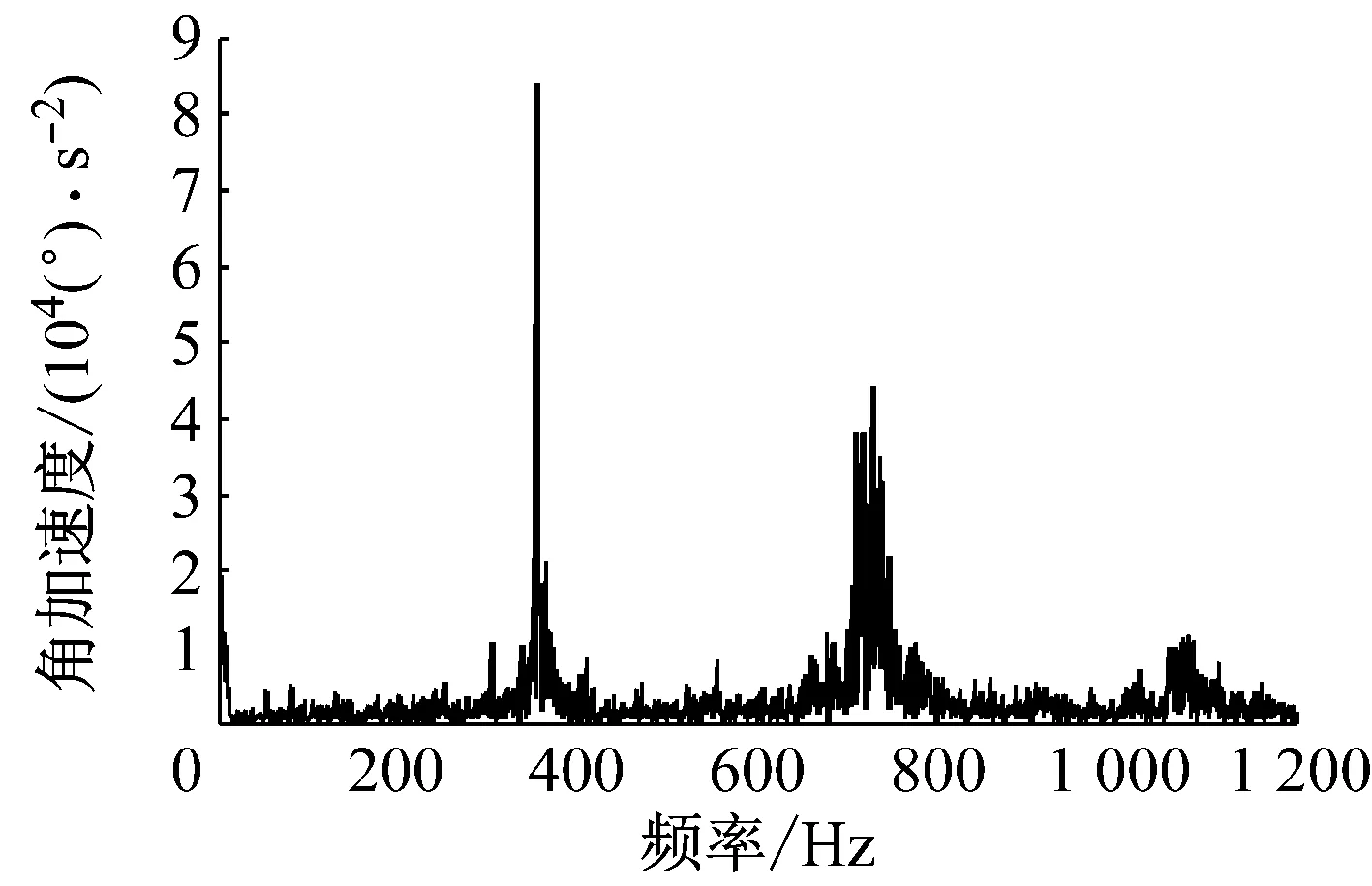
(b) 频域图

从图3(a)所示可以看出，在摇臂传动系统空载状态下，系统所受最大振动幅值发生在0～0.1 s区间内，在0.1 s以后系统振动逐渐恢复平稳，但是从振动加速度幅值变化情况看系统振动依然较为明显。这主要是由于齿轮传动系统内部各齿轮啮合时产生的刚度激励造成的。图3(b)所示为空载情况下Z4质心扭振的频域图，从图中可以看出,角加速度幅值较大处对应的频率分别为360.2 Hz、721 Hz、1 082 Hz、其中360.2 Hz与第二级齿轮啮合频率360.38 Hz接近，角加速度幅值较大处分别出现在第二级齿轮啮合频率1倍频、2倍频、3倍频处，可以看出空载情况下，系统振动响应主要受啮合频率的影响较大。

当系统输入扭矩值为F=1.35×105N·m时的Z4质心扭振的时域图和频域图如图4所示，从图4(a)可以看出系统启动时对角加速度幅值的影响明显减小，没有出现较大的幅值突变，系统进入平稳运行阶段后，角加速度的幅值较空载时明显增大；从图4(b)可以看出，系统虽然也出现了第二级齿轮啮合频率1倍频、2倍频、3倍频，但是3倍频的幅值明显减小，1倍频对应幅值明显增大，于此同时出现了一级齿轮啮合频率的1倍频739.9 Hz，幅值为2.73×104(°)/s2，说明此时一级传动已经对二级传动响应产生了影响。

(a) 时域图

(b) 频域图

当系统输入扭矩为滚筒额定值，即F=2.7×105N·m时，Z4质心扭振的时域图和频域图如图5所示，从图5(a)可以看出系统启动时角加速度也没有出现较大的幅值突变，系统进入平稳运行阶段后，角加速度的幅值比其在上述两种工况中的明显增大；从图5(b)可以看出，系统虽然也出现了第二级齿轮啮合频率1倍频、2倍频，但是3倍频的幅值已经不具有明显特征，1倍频对应幅值达到最大，同时出现了一级齿轮啮合频率的1倍频739.9 Hz，幅值增大至5.48×104(°)/s2，说明随着外载荷的不断增加，一级传动啮合刚度激励对二级传动振动响应影响逐渐增大。

4 结语

通过建立采煤机摇臂齿轮传动系统的动力学仿真模型，分别研究了摇臂传动系统在空载和不同变载情况的振动响应情况，并应用MATLAB软件对仿真数据进行数值分析。分析结果表明：

1) 摇臂齿轮传动系统在空载情况下，最大激励振动发生在启动阶段，随着输入载荷的不断增加，启动阶段的振动幅值逐渐减小，但是系统平稳运行后的振动幅值逐渐增大，当输入载荷为滚筒额定转矩时振动幅值达到最大。

2) 在系统的频谱分析中发现随着输入载荷的增大，一级齿轮啮合频率的对应角加速度幅值随之增大，并且一级传动啮合刚度激励对二级传动振动响应影响也逐渐增大。