基于谱聚类提取与数据场模型融合的提升机故障分析

仝部雷

(山西省煤炭职工培训中心， 山西 太原 030006)

0 引言

针对提升机工作中出现的故障，目前常见的诊断方法主要包含解析模式，信号处理模式，智能处理技术。其中谱聚类方法是智能处理技术中的一项研究重点，其基于对数据集中的数据进行特征向量及特征值的求解方式进行算法实现。谱聚类方法的优点包含有：数据集合大小的敏感性和数据集合维度的无关性，从而不会产生因为维度问题带来的奇异解。此外该方法不以假设方式构建数据的全局结构，从而不会生成局部最优解的情况。首先通过数据场模型对样本集合中的孤立数据进行清除，然后再根据数据场模型的设计确定聚类节点个数及聚类分类数，最后再通过K-means算法进行无监督方式下的样本点划分。文中通过UCI公开数据集与提升机发生轴承故障时所产生的数据集进行了方法验证，实验结果显示将谱聚类技术与数据场模型的融合有效提升了提升机的故障诊断能力。

1 数据场模型的创建

数据场模型，主要是对对象间的非直观作用所产生的数据进行建模，从而生成提升机工作中所各个数据间的聚类特性。故文中对故障数据采用了数据场建模方式来对数据间的关系进行描述。同时分别从势、场强及梯度等特征进行了研究。

数据集合中，已知样本集为{X1,X2,…,Xn}和样本数据所生成的数据场。该数据集中的样本个数值为n，那么由这些样本所生成的势值计算公式为：

(1)

影响因子作用于每个样本值的势。式中的δ与e值成正比例关系，在两者的均极小的情况下所得到的势值之和也会是最小值，反之同样成立。因此为式子选取一个符合要求的δ，对于确定样本势值的分布具有重要意义，文中对该参数的选取采用势熵法。

2 谱聚类改进方法下的提升机故障诊断分析

针对无监督谱聚类算法所存在的问题，文中基于数据场模型研究了谱聚类算法的改进方法。首先通过数据场模型对样本集合中的孤立数据进行清除，然后再根据数据场模型的设计确定聚类节点个数及聚类分类数，最后再通过K-means算法进行无监督方式下的样本点划分。

2.1 孤立点的判别

数据集中的孤立点值与正常样本点存在较大差异，其分布一般偏离于正常样本点数据。文中通过多次实验得到了一个可用于确认是否为孤立点的阈值，若阈值范围内的点所计算出的势值偏小，即可将其认为是孤立点。孤立点检测的主要方式是根据数据的势值大小来确认，对于满足孤立点定义条件的点称之为孤立点，然后将该点标记为可剔除点。算法步骤为：

输入：样本数据集{X1,X2,…,Xn};

输出：孤立点数据集合。

步骤：

1) 根据数据集{X1,X2,…,Xn}的值生成数据场；

2) 通过式子(1)分别生成各样本数据点的场内势值；

3) 对势值进行倒排，取最后值所对应的数据点，然后将其从数据集{X1,X2,…,Xn}中剔除，另存放置孤立点的集合；

4) 重复上述步骤(1)～(3)，直到样本内所有孤立点被剔除完毕。

2.2 确定初始化聚类数与聚类中心

数据场的大小可以体现出数据各样本间所存在的互相作用关系，势值是通过对样本点的作用力进行求和所得，其值大小对于数据在整个样本空间的重要性进行了解释，同时势心的大小确定了数据样本的重心，一般情况下可称之为“准数据重心”。势心值的大小直接确定出了合理的聚类个数及中心点值，有利于后期进行无监督分类的组数确定。无孤立点所构成的纯净样本点，其初始参数确认的流程为：

输入：不包含孤立点之外的其他样本数据集{X1,X2,…,Xn};

输出：合理的聚类数k，各聚类的中心点集合

步骤：

1) 根据数据集{X1,X2,…,Xn}生成样本数据场；

2) 通过式(1)分别生成各个样本数据点的势值，构建势值矩阵F；

3) 通过Hesse矩阵的计算方式生成矩阵特征值及最大值点，最后对聚类数k和中心点进行计算。

2.3 故障诊断

改进谱聚类方法下的故障诊断技术的流程为：

1) 生成数据样本集{X1,X2,…,Xn}的相似矩阵W∈Rn×n，其中Wij=exp[-d(xi,xj/2δ2)]。

2) 对相似矩阵构建拉普拉斯矩阵L，L=D-1/2WD-1/2,其中D表示为有Wij所构建的对角矩阵。

3) 基于2.2部分计算初始化K及中心点的方式求得中心数据集为C=[c1,c2,…,ck]。

4) 生成拉普拉斯矩阵的特征值和特征向量，选取前k个特征值所对应的特征向量构建矩阵Z∈Rn×k。

5) 对最终构建的矩阵Z采用归一化方式进行值处理得到矩阵Y。

6) 其中矩阵Y的行对应于某一个样本数据，通过步骤(3)中的处理方式生成样本中心集合C,并根据C值和初始化k值进行聚类处理。

7) 对数据样本集进行类别的划分，若Xi被聚类到第j类中，即表示矩阵Y中的i行被分到了j聚类中。

3 仿真实验

文中通过UCI公开数据集与提升机发生轴承故障时所产生的数据集进行方法有效性的验证。另外也将K-means聚类算法，传统谱聚类NJW作为验证文中所提出的算法有效性baseline。文中实验平台中的处理器为2.94 Hz，内存和硬盘大小分别为3GB和320GB，采用Matlab编程方式在window 7系统中进行程序的处理，最后对每个实验进行30次处理，取其平均值作为最终结果。另外采用F-measure作为性能评判的指标。

3.1 UCI公开数据集

Iris数据集根据其分布可将其划分为3类，平均每类中的数据样本个数为50，其中每个类别表示的是不同的鸢尾花类型。Wine数据集根据其分布可将其划分为3类，每类中的数据样本个数根据其特征的不同而不同。Zoo数据集根据其分布可将其划分为7类，样本总大小为101。图1所示为Iris数据集分别在3种不同聚类算法中的F-score大小，从曲线变化中可以看出，与K-means聚类算法相比，NJW算法更加略胜一筹；NJW-Fields算法的效果比另两者算法结果都好。

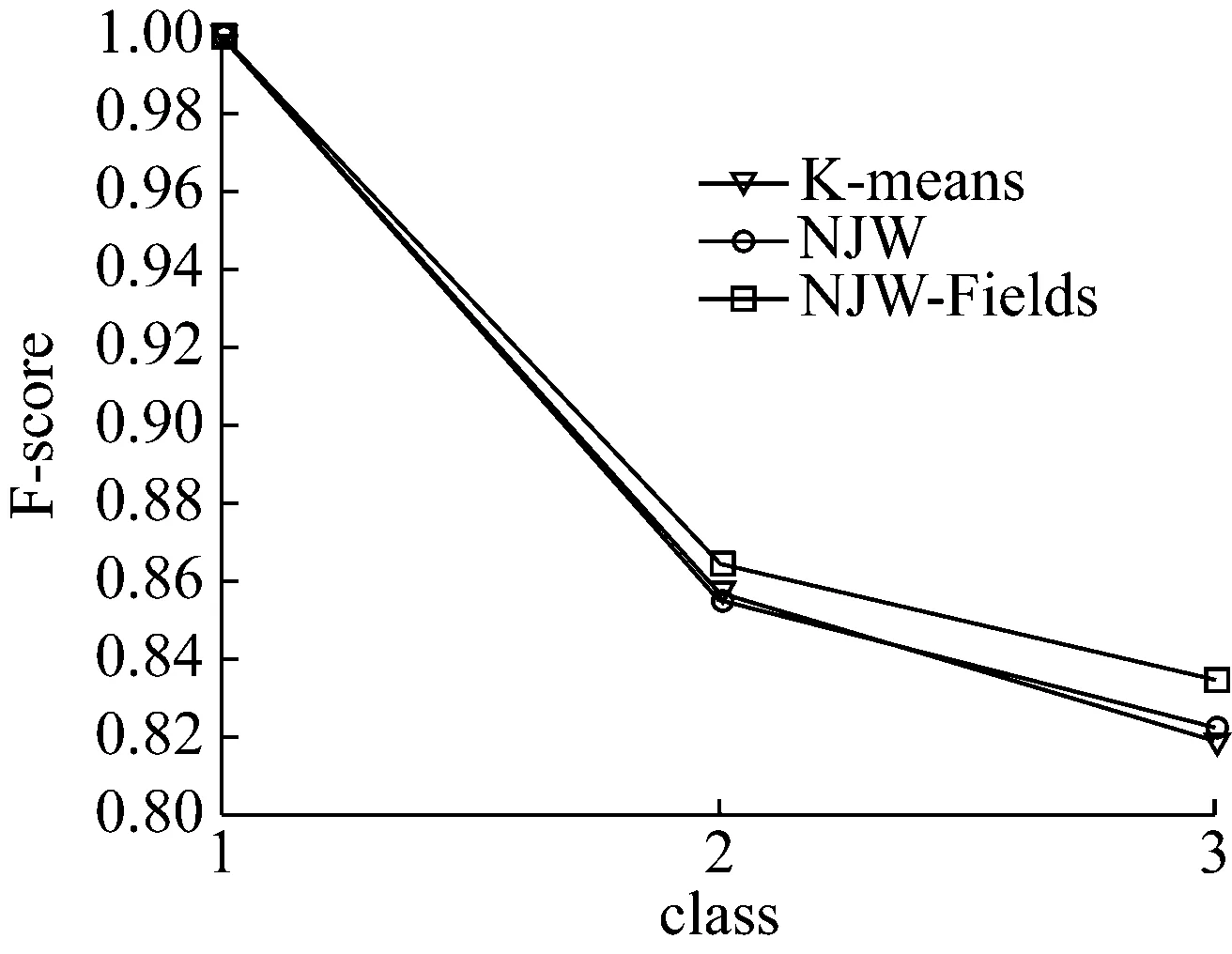
图1 Iris数据集在不同算法下的F-score

图2所示为Wine数据集分别在3种不同聚类算法中的F-score大小，与图1聚类所得的效果相似，即NJW-Fields算法的聚类结果优于传统的K-means聚类算法和传统谱聚类NJW。再一次说明了文中针对谱聚类算法的改进是有效的，即能够拥有比较好的数据聚类结果。

图3所示为Zoo数据集分别在3种不同聚类算法中的F-score大小。从变化曲线可以看出，该样本数据之间存在线性不可分的关系，因此在传统的K-means聚类算法对于聚类个数3类和7类所得到的聚类结果与其他的相比，结果相对来说比较差，另外NJW谱聚类算法在聚类个数为3类时的结果不理想，当聚类个数为其他值时，另外两者传统聚类算法也未得到比较好的结果。但是文中所提出的改进方法NJW-Fields聚类算法对于不同的聚类个数，其结果表现的都比较均匀，聚类效果也好于其他聚类结果。

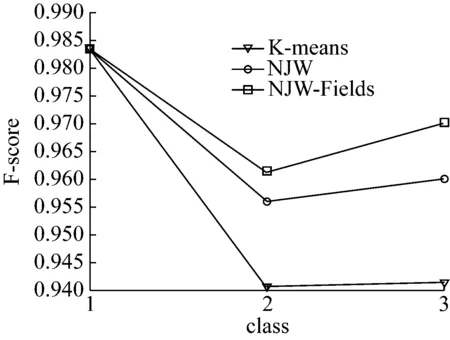
图2 Wine数据集在不同算法下的F-score

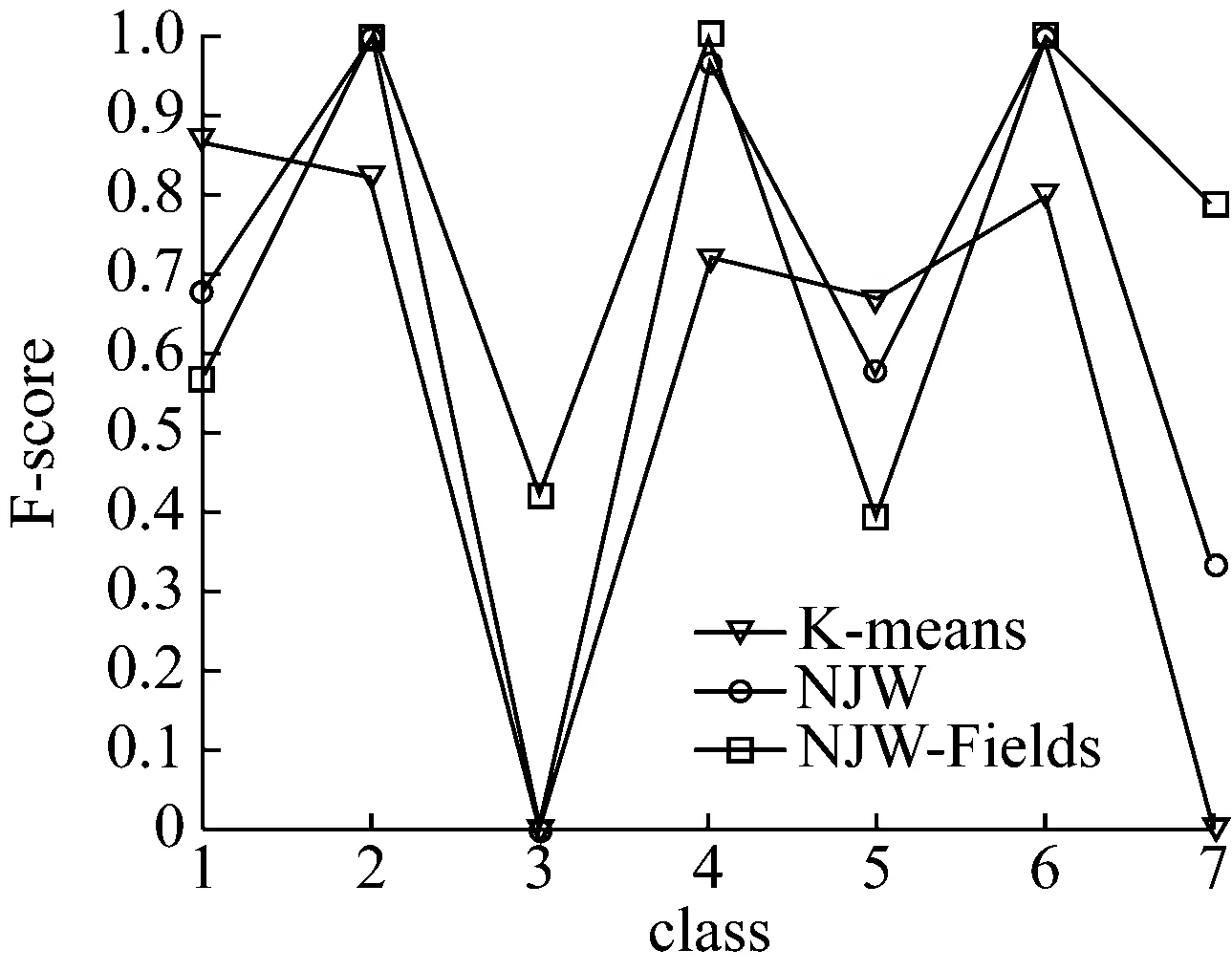
图3 Zoo数据集在不同算法下的F-score

表1对文中所采用的3个聚类算法在不同数据集中的MacroF1值进行统计说明，对于在聚类开始执行之前，通过设置默认参数的方式加入了聚类个数k及每个聚类中的中心点，其所得的聚类结果优于其它未加入设置默认参数的聚类结果。表2对文中所采用的3个聚类算法在不同数据集中的所用时长进行了统计说明，从其结果显示来看,K-means算法所消耗的时间是3个算法中最长的，而NJW聚类算法由于在其处理过程中加入了Laplace矩阵，同时根据其特征值排序选取前k个向量，使其成为聚类数据集，因此对于聚类所需的时长有明显的缩短，所需处理时间变小。此外对于改进的NJW-Fields算法，其在聚类开始执行之前，通过设置默认参数的方式加入了聚类个数k及每个聚类中的中心点，从算法处理时长的对比上来看，该类型算法所消耗的时长明显减小。

3.2 提升机轴承故障数据集

对提升机在日常生产中的故障数据进行搜集和整理，对数据集中的数据进行了清洗及预处理操作，对数据集中的数据通过选取的方式生成了文中需要研究的故障数据集。整理后数据集中总共分为5种常见的故障，不同故障下的数据样本个数为1 630，每个数据均通过10个维度的特征进行表示。表3对整理的故障数据进行了部分举例说明。分别对搜集得到的故障数据进行K-means聚类算法、传统NJW谱聚类算法、改进后的NJW-Fields聚类算法处理，所需消耗的时间与生成结果的MacroF1值如表4和5所示。

表1 不同算法在不同数据集中的MacroF1结果比较

表2 不同算法在不同数据集中的运行时长结果比较

表4为采集所得提升机在发生故障时的数据集，该数据样本集分别在K-means聚类算法、NJW谱聚类算法、文中改进的NJW-Fields聚类算法所消耗的时长统计，从统计结果来看，K-means聚类算法在聚类处理过程中需要较长的时间，NJW谱聚类算法所需要的时长明显小于K-means聚类算法在聚类处理过程中的所需时长。此外,文中所提出的NJW-Fields聚类算法是3个算法中所需消耗时间最短的方法。

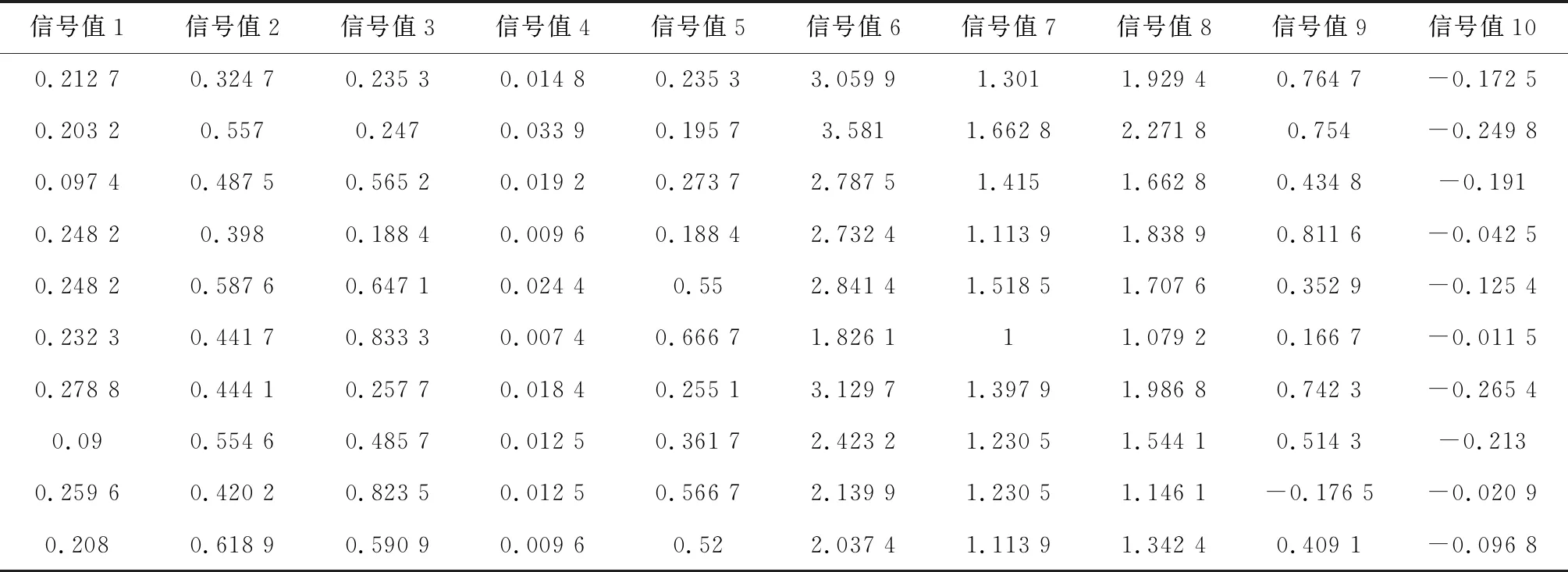
表3 代表性故障信号的数据信息

表4 不同算法运行所需时间对比

表5 不同算法聚类结果的MacroF1值对比

表5为采集所得提升机在发生故障时的数据集，该数据样本集分别在K-means聚类算法、NJW谱聚类算法、文中改进的NJW-Fields聚类算法所得结果的F-measure统计，从表中可以看出，K-means聚类算法所得到的分值最低，为0.572 8；NJW谱聚类算法所得的F-measure分值为0.618 3，其值属于中等;文中所提出的NJW-Fields聚类算法所得到的F-measure分值为0.657 1，其值是3种算法中的最大值。由于F-measure分值的大小往往表示的是算法效果的强弱，由此可以看出文中所设计的NJW-Fields聚类算法优于其他两种传统方式的聚类算法。

4 结语

文中采用将谱聚类技术与数据场模型进行融合技术，通过迁移数据场模型的优势与改进谱聚类算法在聚类过程中的劣势的方式，对提升机出现的故障问题诊断进行了有效的提升。改进的谱聚类算法首先通过数据场模型对样本集合中的孤立数据进行清除，然后再根据数据场模型的设计确定聚类节点个数及聚类分类数，最后再通过K-means算法进行无监督方式下的样本点划分。

通过UCI公开数据集与提升机发生轴承故障时所产生的数据集进行了有效的实验验证，实验结果显示将谱聚类技术与数据场模型的融合有效提升了提升机的故障诊断能力。