铝型材拉弯成形数值模拟及工艺优化

郭浩宇,闫晓磊,陈昌荣，练国富,黄旭,冯美艳

(1.福建工程学院 机械与汽车工程学院,福建 福州350118；2.福建省汽车电子与电驱动重点实验室，福建 福州350118)

铝型材具有密度低、强度高、抗冲击性能好、易回收等优点，广泛应用于汽车安全部件和框架式车身的制造[1]。拉弯成形是铝型材的一种重要加工形式。铝型材在拉弯过程中容易产生起皱、破裂、回弹等缺陷，使得最终成型的拉弯件在尺寸和形状精度都很难达到设计的要求，如何确保型材成型质量的稳定可靠是弯曲成型件的主要问题。

一般可以通过仿真与实验相结合的手段进行工艺优化来提高型材拉弯后的成型质量[2]。Finn等[3]研究了车身零件弯曲成形回弹数值模拟方法，提出在仿真的不同阶段采用不同的算法可以更加接近实际的生产情况；Arid H. Clausen等[4]利用有限元软件，分析了不同型材截面大小对铝型材回弹和畸变的影响规律。JoungsikSuh等[5]通过研究拉伸方法和拉伸长度对回弹进行有限元模拟，结果表明在弯曲前进行预拉和弯曲后进行补拉可以有效地改善型材的成型质量；Gu等[6]研究了不同成形曲率下的铝型材回弹情况；杜建宁等[7]针对常用铝合金型材零件进行研究，预测了型材在成形过程中容易出现问题的区域，验证了数值模拟回弹过程的准确性。卜晓珍等[8]利用有限元软件对π截面铝型材进行了拉弯仿真，分析了预拉和补拉对铝型材回弹的影响规律。

目前，针对铝型材拉弯成形工艺数值模拟的分析研究还不够完善，少有考虑包覆拉伸对型材回弹后的影响。本文基于有限元方法，对A6043系的汽车行李架结构件进行拉弯成形仿真模拟，研究其位移控制拉弯成形的工艺，分析了不同条件下的预拉、包覆拉、补拉和摩擦系数对汽车行李架成型件回弹的影响规律。根据影响成型质量的规律优化工艺参数，有效减少试验的次数，降低企业生产成本，为此类零件生产的工艺参数优化提供参考。

1 拉弯成形工艺

1.1 基本原理

拉弯成形工艺与其他成形工艺相比成本低，适合加工变曲率大的型材。型材拉弯是将型材在一定的弯曲条件下压入模具成型的弯曲过程[9]，如图1所示。通常采用的拉弯加载方式有3种：分别为预拉-弯曲(P-M)、弯曲-补拉(M-P)、预拉-弯曲-补拉(P-M-P)，根据现有研究表明，P-M-P的拉弯成型方式成型质量最好，因为弯曲前施加一定的预拉力可以使型材进入塑性阶段，适当的拉伸量能有效改善成型的应力分布状态，减少成形后的缺陷[10]。

图1 拉弯加工原理图Fig.1 Schematic diagram of stretch bending processing

1.2 回弹

拉弯成形过程相对比较复杂，影响因素较多，比如型材的材料属性，零件的形状和大小，成型的温度及工艺参数等[9]。对于汽车行李架结构件而言，拉弯卸载后回弹量大小是评价一款行李架最终成型效果的重要评价指标之一。本文研究的回弹是指拉弯卸载前后型材的形状发生变化所引起的现象，回弹量以卸载前后型材两端的间距d0来描述，如图2所示。

图2 回弹卸载前后变化图Fig.2 Changes before and after springback unloading

2 拉弯成形有限元模型的建立

2.1 材料模型

汽车行李架采用A6043系铝型材，金属材料拉伸测试依据室温测试的国家标准(GB/T 228.1-2012)，在电子拉力试验机(Instron，LEGEND 2382)上以2 mm/min的拉伸速率进行准静态拉伸，得到如图3所示的真应力-应变曲线图。根据Krupkowsky方程：

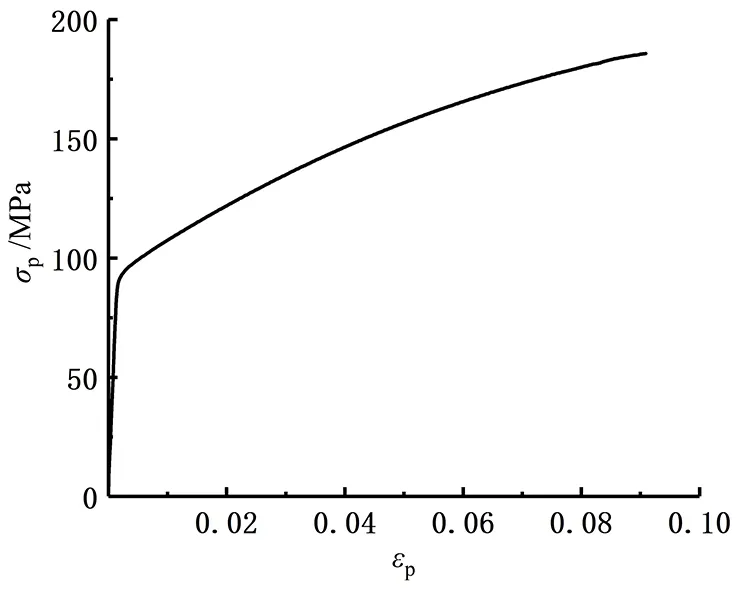
图3 A6043真应力-应变曲线Fig.3 A6043 true stress-strain curve

σ=K(ε+ε0)n

(1)

其中，K为强度系数；n为应变强化指数。建立塑性变形中的应力σp与应变εp之间的本构关系和非线性拟合，获得A6043铝型材力学性能参数如表1所示。

表1 A6043铝型材力学性能参数Tab.1 Mechanical properties of A6043

2.2 数值模拟建模

利用ABAQUS软件数值模拟汽车行李架的加工过程，汽车行李架与其他拉弯成形件相比形状和截面都不规则，以不规则回形截面铝型材为研究对象，建立如图4所示的装配体模型，该模型由铝型材件、夹钳和模具组成。由于结构关于中心面对称，故采用1/2模型，减少计算时间。

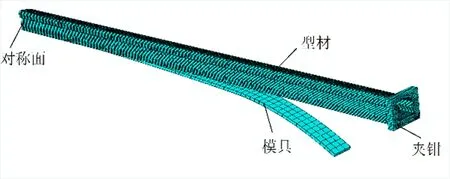
图4 拉弯有限元模型Fig.4 Stretch-bending finite element model

拉弯成形过程主要分成3个阶段：预拉、弯曲包覆拉和补拉。为了使仿真过程与实际结果更加贴近，不同阶段算法也不同，拉弯过程为大变形阶段，采用动态显示算法，考虑其几何非线性，卸载过程用静力隐式算法。以C3D8R为型材实体单元网格，C3D4为模具和夹钳的单元网格,其中铝型材的网格数为20 210个单元，模具和夹钳的网格数分别为110和1 050个单元。

在进行拉弯数值模拟成形的过程中，铝型材与模具一直保持接触，而模具与型材的接触摩擦又是非线性的，所以在ABAQUS仿真过程中模具与型材之间采用硬接触，通用接触算法和库伦摩擦模型。

2.3 夹钳的运动轨迹

在模拟拉弯过程中，型材由夹钳运动的位移轨迹控制，夹钳的运动轨迹可分解成x轴和y轴上的位移。由于型材的模具对称，所以只取一侧进行计算。计算夹钳的轨迹分为两段，先拉弯大弧段，再拉弯小弧段。

如图5所示，待加工件的原始长度为L，模具的大弧半径为R，弧度为α；小弧段半径为r，弧度为β。夹钳在x方向的位移量为f(x)，在y方向的位移量为f(y)。

图5 位移加载轨迹示意图Fig.5 Schematic diagram of displacement loading trajectory

在图5中，假设预拉量为Δl1,包覆拉伸量为Δl2，补拉量为Δl3，预拉结束后夹钳的坐标位置是：

f(x)=L+Δl1

(2)

f(y)=0

(3)

预拉结束后型材的长度为L+Δl1，弯曲包覆拉伸结束后夹钳的坐标位置是：

f(x)=Rsinα+rsin(α+β)-rsinα+

(L+Δl1+Δl2-Rα-rβ)cos(α+β)

(4)

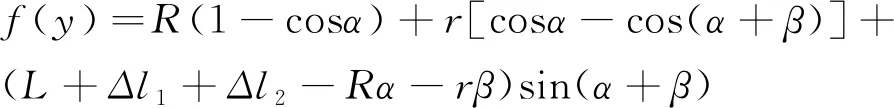
(5)

补拉结束后夹钳的坐标位置是：

(6)

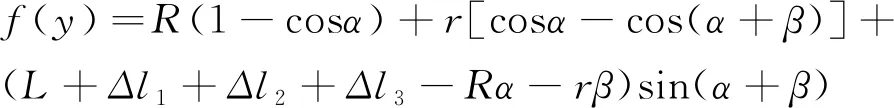
(7)

3 试验方案

3.1 拉弯工艺参数的选择

根据汽车行李架铝型材零件的成形特点，预拉量、包覆拉伸量、补拉量和摩擦力的大小都会影响型材的最终成型质量，目前研究拉弯成形工艺参数优化一般不考虑它们之间的交互影响[11-12]。预拉和补拉可以有效改善型材内部的应力分布情况，一般限定在0.2%～1%之间，型材弯曲的包覆拉伸阶段是其主要变形阶段，造成成形材料起皱和断裂现象的主要原因是拉伸量过大，一般拉伸量限定在1%～3%之间，摩擦系数在生产过程中也会有所波动。拉弯成形水平因素如表2所示。

表2 拉弯成形水平因素取值表Tab.2 Factor levels for stretch forming

3.2 正交试验设计

正交试验是一种研究多因素多水平的试验方法，有助于减少试验数量并通过正交矩阵寻找最佳工艺参数组合，改善型材的成型质量，从而减少试验的成本和时间[13]。根据因素和水平的数目，本次所选用的正交试验设计表为四因素三水平表格L9(34)，共计9组试验，各试验水平如表3所示。

表3 正交试验表Tab.3 Orthogonal experiment table

4 结果与分析

4.1 试验结果

通过数值模拟分析研究不同工艺参数对不规则截面汽车行李架零件成形质量的影响规律，正交试验数据及结果如表4所示。

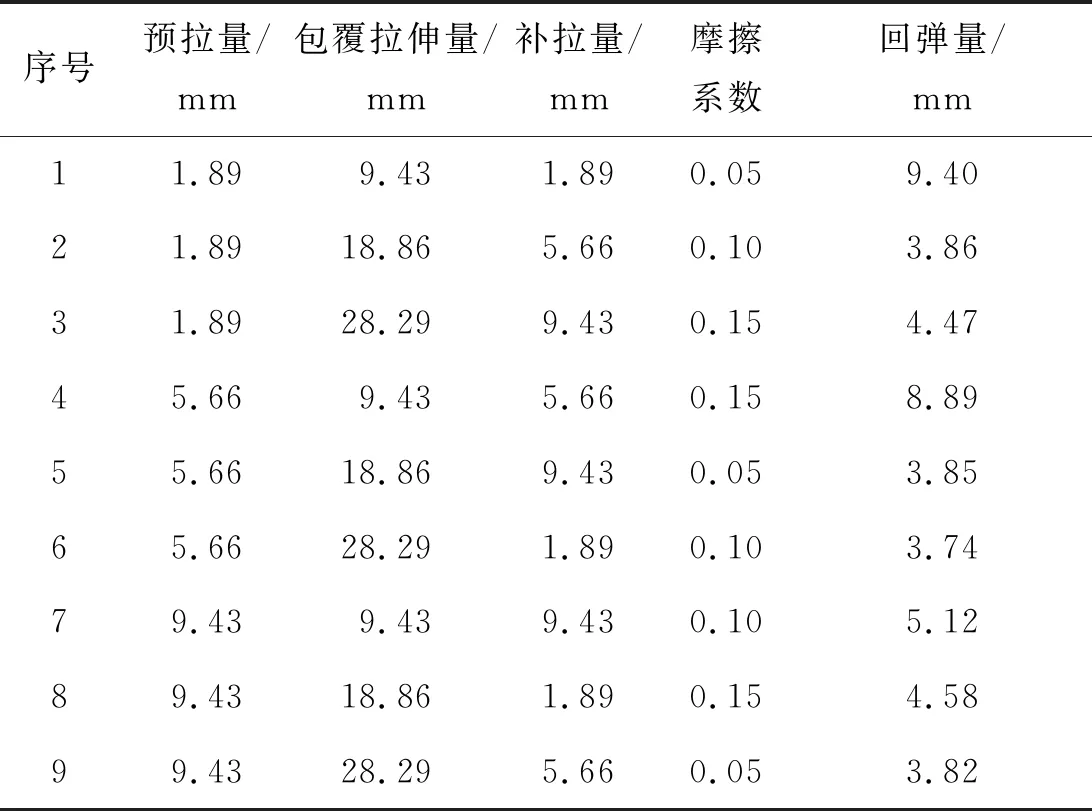
表4 正交试验结果Tab.4 Results of orthogonal experiments

4.2 极差分析

根据极差的计算公式对正交数据进行处理，得到4个工艺参数极差值如表5所示。

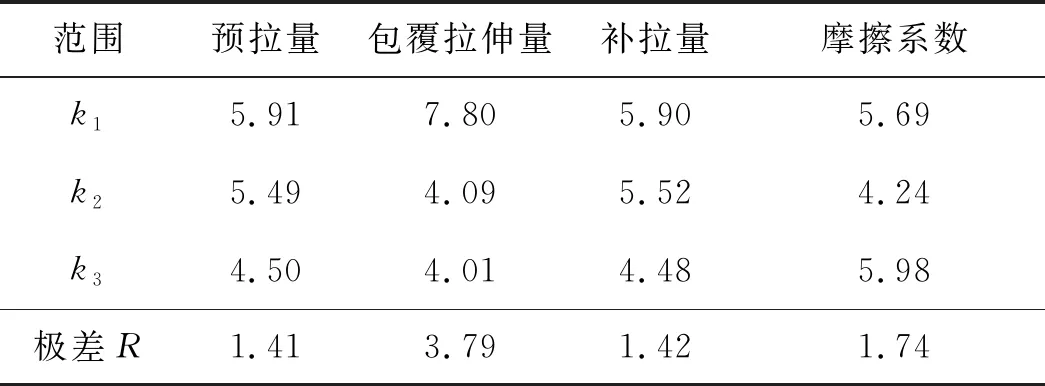
表5 极差分析结果Tab.5 Range analysis results

通过对极差结果的分析，包覆拉伸量是影响回弹的主要因素，摩擦系数、补拉量和预拉量影响较为显著。

4.3 工艺参数影响分析

预拉量对回弹量的影响趋势如图6所示，回弹量与预拉量呈现初负相关，预拉量越大，回弹量越小。预拉量从0.2%增大到1%的过程中，回弹量减少较为显著。主要是因为预拉量越大，型材越容易进入塑性状态，在拉弯卸载后弹性变形区域减少从而减少回弹量[2]。

图6 回弹量随预拉量的变化Fig.6 Variance of the amount of springback varies with the amount of pretension

图7是型材回弹大小随包覆拉伸量变化的趋势图，当包覆拉伸量从1%增大到3%时，回弹量减少明显。由于包覆拉伸阶段是型材弯曲的贴模阶段，型材的主要变形就在包覆阶段，改善包覆拉伸量可以有效改善铝型材内部的应力状态，使塑性变形部分减少，降低回弹量[14]。

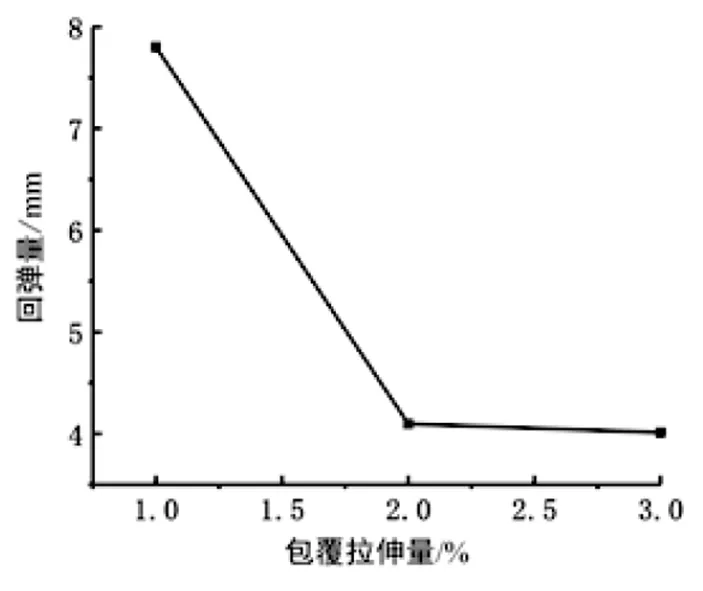
图7 回弹量随包覆拉伸量的变化Fig.7 Variance of springback with the amount of coating stretch

随着补拉量增大，型材回弹大小随补拉量的变化如图8所示，当补拉量从0.2%增大到1%时，回弹量一直是下降的趋势。通过控制补拉量的大小可以改善型材中的应力分布情况，加大补拉量可以使型材的应力分布情况变得更均匀[2]。

图8 回弹量随补拉量的变化Fig.8 Variance of the amount of springback with the amount of supplementary stretch

摩擦系数对回弹量的影响如图9所示。摩擦系数为0.1时，型材的回弹量最小。摩擦系数的增大对回弹量的影响较为明显，且与摩擦系数呈正相关性。摩擦系数越大，相同的拉伸量需要克服的摩擦力越大，以至于型材在塑性变形区域较小，且摩擦力会对型材拉伸有一定的抑制作用，使得型材表面受力分布不均匀。所以在拉弯过程中减少不必要的摩擦因素可以改善型材成型后的回弹量[8]。

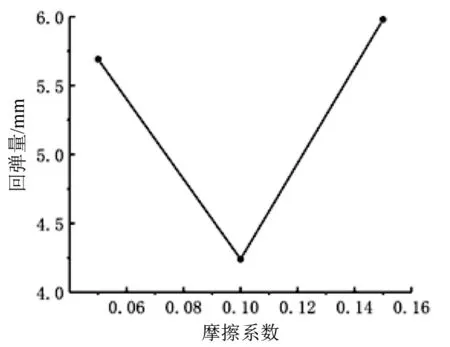
图9 回弹量随摩擦系数的变化Fig.9 Variance of the amount of springback with the coefficient of friction

从正交试验结果可得出拉弯的最佳工艺参数为：摩擦系数0.1，预拉量和补拉量1%，包覆拉伸量3%。针对最佳工艺参数进行了验证试验，试验表明，最佳工艺参数情况下的拉弯成型件回弹量为3.47 mm，回弹量最小。如图10标注位置所示。

图10 回弹量云图(预拉量1%，补拉量1%，包覆拉伸量3%，摩擦系数0.1)Fig.10 Nephogram of springback amount (pre-stretching amount 1%, supplementary stretch amount 1%, coating stretch amount 3%, friction coefficient 0.1)

4.4 包覆拉伸量单因素分析

通过正交试验分析可知，在拉弯过程中，包覆拉伸量对型材的成型质量影响最大，在保证其他几个因素都是最优的情况下，对包覆拉伸量做单因素分析，分析包覆拉伸量分别为1%、2%、3%、4%、5%、6%、7%的回弹量，得到关于包覆拉伸量与回弹量的一元非线性方程：

y=9.58×exp(-x/0.56)+3.45Δ

(8)

函数关系、方程(8)与试验结果散点值的结果拟合度R2达0.999，符合实际的变化规律。如图11所示，当包覆拉伸量达到3%以后，超过了材料的屈服应力，进入塑性变形阶段，回弹量趋于稳定，再增加包覆拉伸量对改善回弹作用不大。在其他工艺参数相同，分别为预拉量1%、补拉量1%、摩擦系数0.1时，对1%和7%包覆拉伸量的型材进行仿真模拟，得到应力云图如图12所示。从应力云图可以看出，改变包覆拉伸量可以有效改善铝型材内部的应力状态，使塑性变形和卸载后弹性变形部分减少，降低成形后的回弹量。

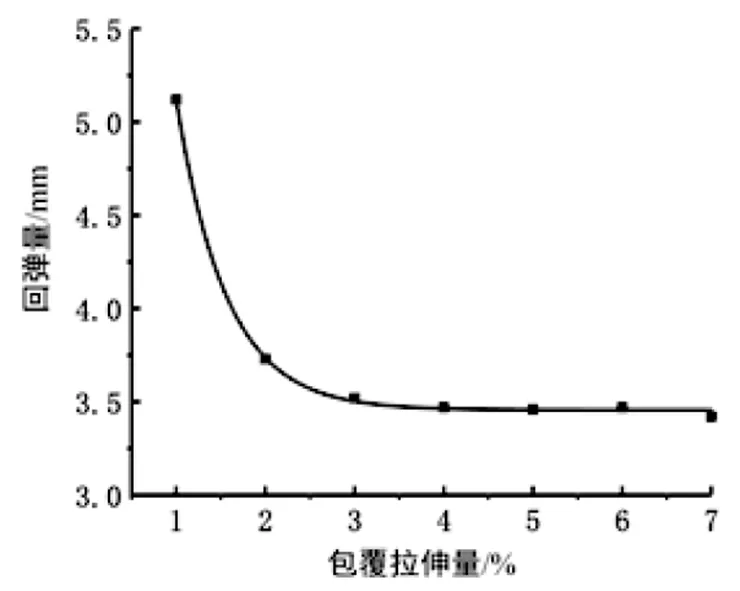
图11 回弹量随包覆拉伸量的变化(预拉量1%，补拉量1%)Fig.11 Change of springback with the coating stretch amount (pre-stretching 1%, supplementary stretch 1%)

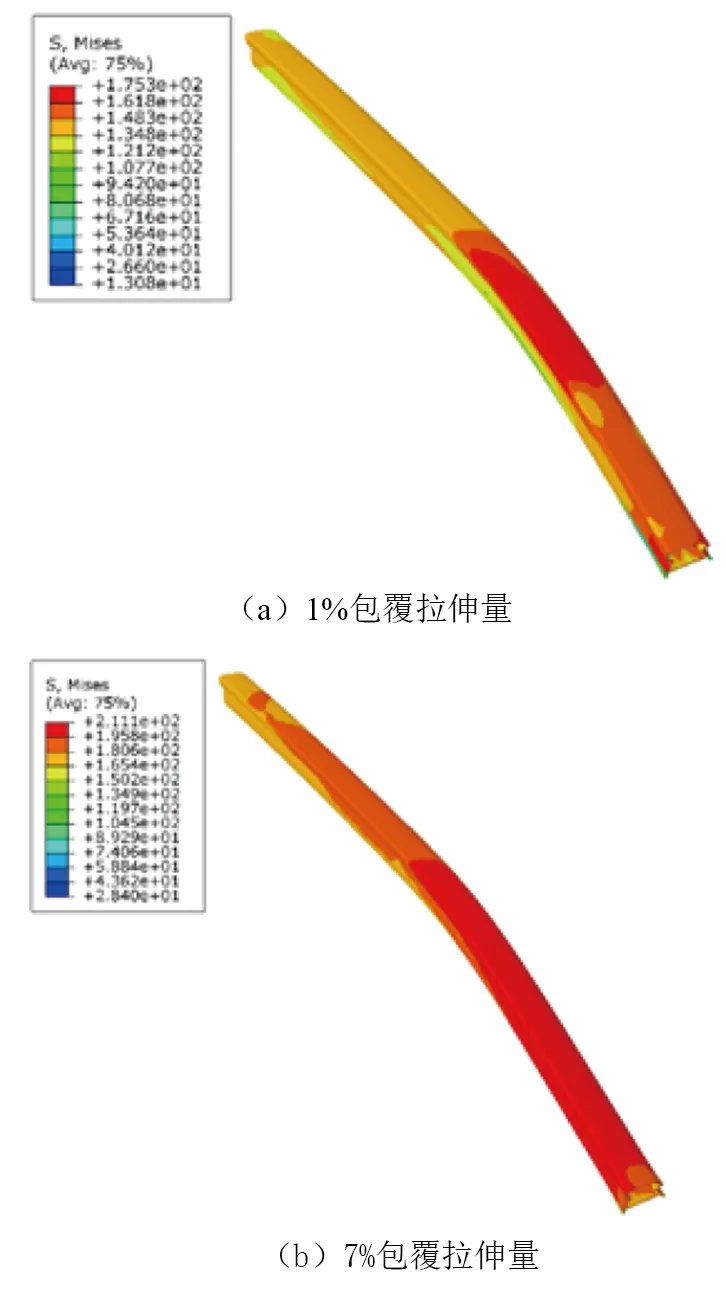
图12 不同包覆拉伸量的应力云图Fig.12 Stress nephogram of different coating stretches

5 结论

1)回弹量与预拉量、包覆拉伸量、补拉量呈负相关性，与摩擦系数成先减小后增大的趋势。

2)通过正交实验得到最佳工艺参数：预拉量为1%、包覆拉伸量为3%、补拉量为1%、摩擦系数为0.1。在最佳工艺参数下，汽车不规则铝型材行李架的拉弯成形回弹量最小。

3)包覆拉伸量对回弹量的影响最为显著，且回弹量随包覆拉伸量的增大而降低；通过包覆拉伸量单因素分析，发现包覆拉伸量超过3%后，回弹量趋于稳定。