RuO2-CeO2复合氧化物相分离现象与本质的分析

王欣, 王虎, 唐中帜, 周扬杰, 唐电1,

(1.福州大学 材料科学与工程学院,福建 福州 350108；2.福州大学 材料研究所,福建 福州 350108；3.中国科学院功能纳米结构设计与组装重点实验室，福建 福州 350002)

金红石RuO2是最重要的活性氧化物之一，但昂贵的价格限制了其推广应用。研究发现，掺杂其它非贵金属氧化物，在降低材料成本的同时能获得更高活性。其中复合RuO2-CeO2催化剂可追溯至1988年：Imamura等[1]制备的RuO2-CeO2在分解甲醛和甲酸等含氧化合物时活性很高。此后RuO2-CeO2的应用日益广泛[2-3]。

就RuO2-CeO2而言，组织与结构极大影响其催化效能[2-5]。特别在制备RuO2-CeO2过程中，固溶体Ru(1-x)CexO2易分解为(1-x)RuO2+(x)CeO2[3-5]单体而致活性降低。因此了解与掌握RuO2-CeO2相分离本质和规律尤显必要。本团队采用第一性原理计算结合热力学分析的方法，获得多个含Ru氧化物体系[4,6,7]固溶体的结构和能量的数据，预测了含Ru氧化物的spinodal分解。基于研究中还观察到含Ru氧化物的quasi-spinodal现象[4,7]，本文拟在已有工作基础上，着重分析金红石和萤石固溶体Ru(1-x)CexO2的分解能、热力学状态图与界面能，并对723 K热分解制备的3种组成的(分别记为高Ru、中Ru和低Ru)(1-x)RuO2-(x)CeO2样品进行相分析，尝试讨论RuO2-CeO2的quasi-spinodal的分解机制。

1 计算与实验

1.1 材料计算方法

分别计算了金红石 (P42/mnm)和萤石结构(Fm/3m)的Ru(1-x)CexO2，其中x分别为0, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875, 1。采用VASP程序软件包进行基于密度泛函理论(DFT)的第一性原理计算。对金红石和萤石分别建立了2×2×1超胞，见图1。交换关联势采用LDA近似。平面波截断能选取520 eV。采用6×6×6的Monkhoot-Pack特殊点对布里渊区行取样。电子弛豫的能量收敛标准为5×10-3eV/atom。计算在实空间中进行，采用Blöchl四面体方法精确计算系统总能。为得到稳定的计算结果，选择对称元素最多的组态进行几何结构优化，并通过Murnaghan状态方程确定平衡状态的能量数据和折合点阵参数。采用热力学方法，进一步计算金红石和萤石相Ru(1-x)CexO2的混合焓和混合自由能，详细过程参见文献[6-7]。

图1 2×2×1超胞结构Fig.1 Structure of 2×2×1 super-cell

1.2 材料制备与相分析

以唐山银河化工厂的RuCl3(ωRu=36.9%)和阿尔法埃莎(Alfa Aesar)公司的CeCl3(纯度为98%)为原料。按Ru∶Ce摩尔比为8∶2、5∶5和2∶8称取药品，溶于无水乙醇溶剂，超声振荡使之充分溶解且均匀分散后，静置12 h。用移液管将涂液均匀涂覆在1.5 mm厚的洁净工业纯钛(TA2)表面，经红外光干燥，在723 K箱式炉中氧化10 min，出炉空冷，继续涂覆，重复上述操作，直至涂料用尽后退火1 h。所获样品分别为Ru0.8Ce0.2O2、Ru0.5Ce0.5O2和Ru0.2Ce0.8O2(简记为RC82、RC55和RC28)，相分析采用Philips.Xpert-MPDX衍射仪，测试条件为：Co靶(Kα1)，Fe滤波，加速电压40 kV，靶电流100 mA，步长0.02°，扫描速率2°/min。

2 结果分析

2.1 Ru(1-x)CexO2、RuO2和CeO2的结构

离子晶体Ru(1-x)CexO2是由Ru4+和Ce4+相互取代而形成的置换固溶体。通过结构优化和Murnaghan状态方程拟合，可获得平衡状态下不同x的金红石和萤石Ru(1-x)CexO2的单胞体积V0。可以看出，金红石和萤石相的V0虽均随Ce/Ru代位含量x的增加而增大，但与置换固溶体遵循的Vegard定律有偏离，相比之下，金红石相偏离程度较大，见图2。

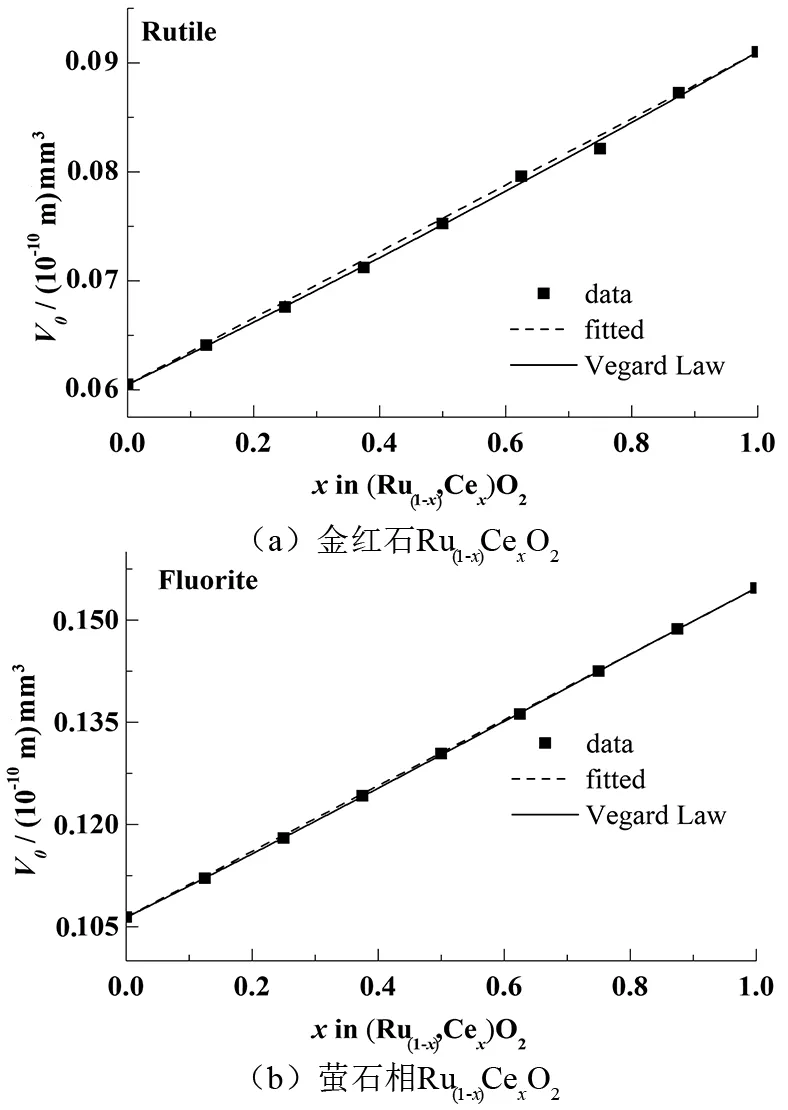
图2 Ru(1-x)CexO2单胞体积V0与组成x的关系曲线Fig.2 Dependence of unit cell volume V0 on composition x for Ru(1-x)CexO2

鉴于固溶体通常无公认和准确的晶体参数数据，为了考察计算结果的可信度，查询了RuO2和CeO2相关文献的计算数据，并与本文结果进行对比。本次计算金红石RuO2点阵参数a(0.443 1 nm)、c(0.308 1 nm)，与文献[8]相对误差分别为0.40%、1.8%；与文献[9]的相对误差则分别为0.045%、0.29%。萤石RuO2点阵参数a(0.443 1 nm)，与文献[10]的相对误差0.042%，与文献[11]的相对误差为2.1%。萤石CeO2的点阵参数a(0.539 8 nm) ，与文献[12]相对误差仅为0.33%，与文献[13]的相对误差仅为0.15%。金红石CeO2的点阵参数a(0.502 5 nm)、c(0.359 8 nm) ，除本次计算结果外未有报导。此外，金红石RuO2点阵参数a、c与标准卡片(JCPDS 40-1290)间相对误差分别仅为1.5%、0.84%。萤石CeO2的点阵参数a(0.539 8 nm)与标准卡片(JCPDS 43-1002)间的相对误差仅为0.22%。由此可认为，本文基于DFT的第一性原理对Ru(1-x)CexO2进行计算，方法可行、数据可信。

2.2 Ru(1-x)CexO2固溶体分解能

处理含活性组元Ru的离子晶体，通常可采用亚晶格模型，即固溶体Ru(1-x)CexO2由组元 (1-x)RuO2和xCeO2二元氧化物复合而成。相应地，固溶体Ru(1-x)CexO2脱溶分解为组元(1-x)RuO2和xCeO2。

温度0 K时Ru(1-x)CexO2的分解能ΔHm，R(x,0)和ΔHm，F(x,0) (R:代表Rutile相; F:代表Fluorite相,下同)可通过公式(1)和(2)计算，并用多项式予以拟合[6,7,14]。

ΔHm,R(x,0)=

54.76x-20.10x2-54.70x3+20.03x4

(1)

ΔHm,F(x,0)=

79.76x-55.67x2-47.92x3+23.83x4

(2)

ΔHm,R(x,T)=ΔHm,R(x,0)+

RT[(1-x)ln(1-x)+xlnx]

(3)

ΔHm,F(x,T)=ΔHm,F(x,0)+

RT[(1-x)ln(1-x)+xlnx]

(4)

其中，T为热力学温度(K)，R为气体常数。

由此，得到0 K和723 K时金红石和萤石相固溶体分解能ΔHm(x,T)与成分x的关系曲线(图3)。由图3可知，ΔHm,R(723 K)和ΔHm,F(723 K)在x为0～1内均为正值，表明金红石和萤石相固溶体具备发生相分离、生成组元RuO2和CeO2的驱动力，这从理论上解释了二元RuO2-CeO2体系常见相分离的实验现象。

图3 Ru(1-x)CexO2的分解能及其拟合曲线Fig.3 Decomposed enthalpy and fitted curves of Ru(1-x)CexO2

2.3 RuO2-CeO2二元体系的热力学状态图

从热力学角度出发，判断固溶体Ru(1-x)CexO2的稳定性及Ru(1-x)CexO2分解时遵循形核-长大还是spinodal机制，需温度TK时，Ru(1-x)CexO2的ΔHm(x,T)-x曲线的一阶导数，并由∂ΔHm(x,T)/∂x=0的边界条件，得到固溶(binodal)曲线；由ΔHm(x,T)-x的二阶导和∂2ΔHm(x,T)/∂x2=0，获spinodal分解曲线。结果见图4。由图4可判断固溶体Ru(1-x)CexO2热力学状态，即状态点位于binodal曲线上方时，Ru(1-x)CexO2固溶体为稳定相；位于binodal曲线和spinodal分解曲线之间的，则固溶体Ru(1-x)CexO2通过形核-长大的方式发生相分离；而位于spinodal分解线下方区域时，固溶体Ru(1-x)CexO2则失稳且自发经spinodal分解机制，生成RuO2和CeO2。

上述理论计算可解释文献[2,3,5]观察的相分离现象。为进一步验证计算的正确性，本文通过常规制备条件获得了723 K热分解温度下的相应样品(见实验部分)。图4表明，723 K时，binodal曲线与纵坐标间无清晰间隙，即此时富Ru(或富Ce)的金红石与萤石固溶体Ru(1-x)CexO2已由形核-长大方式发生分解，生成RuO2和CeO2单体；而Ru与Ce的摩尔比xRu：xCe为0.07～0.98的金红石和0.06～0.98的萤石Ru(1-x)CexO2固溶体，均为热力学不稳相，自发通过spinodal分解机制，生成RuO2和CeO2。由此推断，常规制备条件获得的Ru(1-x)CexO2R和Ru(1-x)CexO2F母相，绝大部分符合自发由spinodal分解发生相分离的热力学判据。因此，本文选择的RC82、RC55和RC28三种成分样品，其中固溶体的分解应遵循spinodal机制。

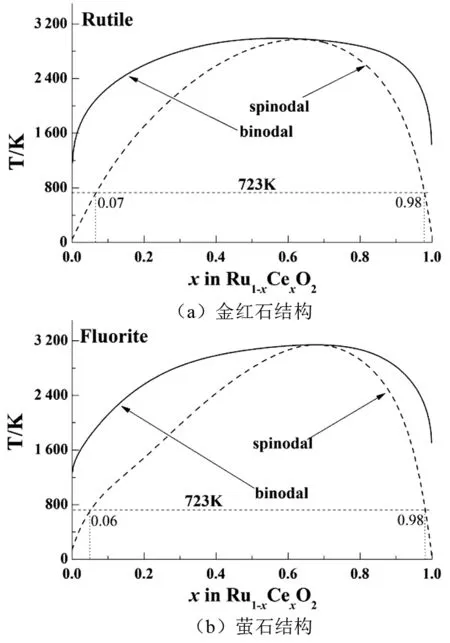
图4 Ru(1-x)CexO2的binodal曲线和spinodal分解曲线Fig.4 binodal and spinodal curves of Ru(1-x)CexO2

2.4 Ru(1-x)CexO2固溶体分解的界面能

进一步细致分析spinodal相变，还需考虑界面能:新相出现增加的界面能是spinodal相变的阻力。按固态相变理论[15]，混合界面能Gm,interface是组成x的函数，还与应变能σ和比表面S有关，用(5)式表达为：

(5)

应变能σ与两相错配度ε有关[10]:

(6)

式中,G为剪切模量，由弹性模量E获得:G=E/2(1+ν)。由于E是组织不敏感参数，故取x=0.5固溶体Ru0.5Ce0.5O2的ER和EF分别为240.2和278.1 GPa[13];ν为泊松比，取0.3;d为晶粒尺度，723 K制备含Ru氧化物涂层，其晶粒尺度d约45 nm，由此计算[2]SR和SF分别为2 452和3 285 m2/mol；ε由(7)式[2,15,16]计算。

(7)

aCeO2和aRuO2分别为RuO2和CeO2晶格常数。Ru(1-x)CexO2R与Ru(1-x)CexO2F分解时的错配度εR和εF,根据由金红石aRRuO2,aRCeO2和萤石aFRuO2,aFCeO2得出。

因此，可以计算Ru(1-x)CexO2R和Ru(1-x)CexO2Fspinodal分解的界面能Gm,interface,R(x)和Gm,interface,F(x)，表述如式(8)、(9)，见图5。

Gm,interface,R(x)=4.47x(1-x)

(8)

Gm,interface,F(x)=3.68x(1-x)

(9)

图5 金红石与萤石结构Ru(1-x)CexO2 spinodal分解界面能Fig.5 Interface enthalpy of rutile and fluorite Ru(1-x)CexO2 in Spinodal decomposition

图6 不同成分配比的Ti/RuO2-CeO2电极样品经723 K烧结后的XRD图谱Fig.6 XRD patterns of Ti/RuO2-CeO2 prepared at 723 K with different composition ratios

2.5 723 K 热分解样品的相分析

制备了3种具代表性(RC82、RC55和RC28)的样品，以考察常规热分解温度(723 K)下固溶体的变化情况。图6为样品XRD图谱。因涂层较薄，XRD中均存在Ti基体衍射峰，以此为内标，可确定并修正涂层中其他物相特征峰。

对比标准卡片(JCPDS 40-1290和JCPDS 43-1002)，XRD谱线衍射峰分别与金红石RuO2(110)、(101)和(211)晶面以及萤石CeO2的(111)、(200)、(220)和(311)晶面相对应(见图6)。Ru与Ce含量相当的RC55，样品涂层内仅见单体金红石RuO2和萤石CeO2。富Ru的RC82，涂层中主要为金红石RuO2，但存在CeO2萤石相。富Ce的RC28，萤石CeO2为主要组成相，但可见金红石RuO2衍射峰。XRD结果说明，成分各异的RC55、 RC28和RC82，尽管固溶体相分离驱动力大小不一，但因3样品的成分点均在固溶体Ru(1-x)CexO2的热力学不稳区内，其分解产物均为RuO2R和CeO2F。

在任务下达后，学生会面临一些需要解决的问题，促使他们必须通过教材的指引、相互讨论来解决。学生始终是课堂的主学生可以通过小组之间相互讨论，自己依据教材的指引寻求解决的方法，着重培养学生自主解决问题的能力，具体体，教师只提供适当的指导，帮助和引导学生思考探究，当遇到操作得不到预期效果时，学生习惯寻问邻座的同学，主动和小组成员进行询问和探讨，共同寻常解决问题的办法。

针对XRD结果，首先RuO2-CeO2体系与满足Hume-Rothery定律、可形成无限固溶体的RuO2-SnO2体系不同，RuO2R与CeO2F结构差异明显、不满足Hume-Rothery定律，彼此互溶差[2,3,5]，Ru(1-x)CexO2固溶体的热力学状态不稳定，发生spinodal分解的倾向明显、反应速度快。而RuO2-SnO2体系的spinodal分解虽也普遍存在[6]，但相对易观测到固溶体-经773 K×1 h退火Ru0.45Sn0.55O2分解为固溶Sn4+的RuO2基固溶体和固溶Ru4+的SnO2基固溶体。这也直接导致鲜见报道Ru(1-x)CexO2固溶体的实验文献。

其次RuO2-SnO2的spinodal分解过程中无晶型的转变，即新/母相均为金红石，相变属于标准spinodal过程[6]。在不同于RuO2-SnO2的RuO2-CeO2中，RC82、RC55和RC28经723 K+1 h退火后，产物为不同晶型的RuO2R和CeO2F，即无论母相原始成分为高Ru、中Ru还是低Ru，Ru(1-x)CexO2固溶体的分解产物都是RuO2R和CeO2F，这虽具备spinodal相变亚稳态母相分解成两个稳定态新相的热力学特征，但不符合常规spinodal相变由母相分解为相同结构新相的要求，据此认为Ru(1-x)CexO2的相变应属于quasi-spinodal分解[4]。

3 Quasi-spinodal分解的讨论与分析

3.1 Quasi-spinodal分解

最早的Spinodal概念，由van de Waals于1850年提出。至1967年Cahn在美国金属学会年会的“Spinodal decomposition”主题报告后，国际固态相变会议上均辟有专题。2010年，徐祖耀院士[18]虽对spinodal分解做了综述，但未提及曾零星报导[19-20]的quasi-spinodal分解。Ru(1-x)CexO2quasi-spinodal分解具备常规spinodal反应“失稳分解”的重要特征，但分解产物彼此结构不同。纳米材料存在quasi-spinodal分解产物结构不同的情况,如金红石分解为萤石[4]、fcc分解出β-相[15]以及hcp分解出fcc[2]。quasi-spinodal分解不仅出现在Ru-Ce-O中[4]， Ru-Zr-O体系也如此[7]。本文尝试从热力学、界面能(结构匹配)和分解机制几方面，对Ru(1-x)CexO2的quasi-spinodal做出初步推断。

3.2 Quasi-spinodal反应的分离能

从热力学角度出发，固溶体Ru(1-x)CexO2R的分解有两种选择，第一为常规spinodal分解，即生成 (1-x) RuO2R+ (x)CeO2R，反应分离能见式(1);第二则为quasi-spinodal分解，相变产物为(1-x) RuO2R+ (x)CeO2F，由于形成自由能CeO2F比CeO2R低约5.10 kJ/molatom[4]，则该反应分离能ΔH则可表述为式(10)。同样，萤石固溶体Ru(1-x)CexO2F的quasi-spinodal反应分离能，因RuO2F比RuO2R的形成自由能高约8.20 kJ/molatom[4]，则可表述为式(11)。

49.66x-20.10x2-54.70x3+20.03x4

(10)

87.96x-55.67x2-47.92x3+23.83x4-8.20

(11)

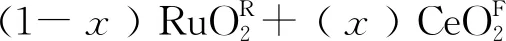
图7 Ru(1-x)CexO2的spinodal和quasi-spinodal分解Fig.7 Spinodal and quasi-spinodal decomposition of Ru(1-x)CexO2

3.3 Quasi-spinodal分解的结构匹配与界面能

一般认为spinodal分解的结构条件是母相与新相结构相同，且有一定的共格匹配以降低界面能，相变无需形核而进行。同样，quasi-spinodal分解也需要共格匹配。以下仍采用反映共格匹配程度的错配度，获得quasi-spinodal分解界面能数据[2,15,16]。

固溶体Ru(1-x)CexO2R经quasi-spinodal分解，产物为RuO2R和CeO2F，分别为体心正方(P42/mnm)和面心立方 (Fm/3m) 结构，见图1。两种结构有相同的阴阳离子比，在一定条件下可以转换：1996年Haines等[21]发现高压时RuO2R转变为RuO2F， 转变通过{101}R‖{100}F、[111]R‖[110]F的切变得以实现，即金红石密排面{101}R和萤石相的{100}F相关联，实现quasi-spinodal分解所需的共格匹配。如此，可利用金红石与萤石密排方向上的阳离子间距差异衡量两相共格程度，即通过以下公式来获得两相的错配度。

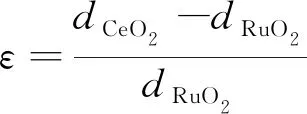
(12)

其中，dCeO2和dRuO2分别为金红石和萤石相密排方向[111]R、[110]F阳离子间距，可由固溶体的具体晶格参数计算得到。并由界面能计算公式(5)获得算出相应界面能，见式(13)和(14)。

Gm,interface,R→R+F(x)=8.23x(1-x)

(13)

Gm,interface,F→R+F(x)=7.02x(1-x)

(14)

通过比较可以发现，quasi-spinodal较spinodal分解的界面能分别提高至1.8与1.9倍，更证实了quasi-spinodal分解因生成新相结构的不同，反应需要克服更高的界面能。

3.4 Quasi-spinodal分解的自由能和相变过程

通过上述针对quasi-spinodal反应分离能和界面能的计算，可得固溶体Ru(1-x)CexO2发生quasi-spinodal分解的总自由能，见式(15)和(16)。

41.43x-11.87x2-54.70x3+20.03x4+

RT[xlnx+(1-x)ln(1-x)]

(15)

89.04x-48.65x2-47.92x3+23.83x4-

8.20+RT[xlnx+(1-x)ln(1-x)]

(16)

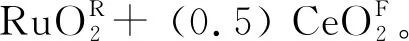
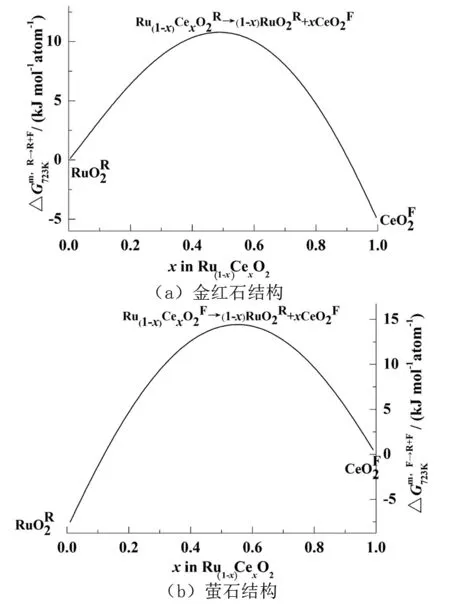
图8 Ru(1-x)CexO2的quasi-spinodal分解曲线Fig.8 Quasi-spinodal curves of Ru(1-x)CexO2

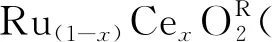
4 结论

2)x为0～1时，固溶体Ru(1-x)CexO2的分解能均大于0，固溶体倾向分解。热力学状态图表明：x为0.07～0.98的Ru(1-x)CexO2R与x为0.06～0.98的Ru(1-x)CexO2F均不稳定，将自发进行spinodal分解，生成端际RuO2+CeO2。

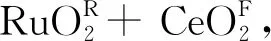
4)对quasi-spinodal反应自由能的计算发现，与常规spinodal分解相比，固溶体Ru(1-x)CexO2选择quasi-spinodal分解后，系统能量更低。初步计算结果与XRD分析一致。