基于有限元的建筑高分子材料热稳定性效果分析
安 昶,孟小丽
(新疆农业职业技术学院,新疆昌吉831100)
近些年我国重要的支柱产业之一便是建筑行业,而建筑中约有90% 左右的建筑物属于非节能型建筑,此类建筑因保温效果不足,导致冬夏两季供暖与制冷所消耗的年均能耗达到我国全部产业总能耗的三分之一,为此需增加节能型建筑,降低我国的能源消耗[1]。随着高分子技术的不断发展,更多的高分子材料类别逐渐出现在不同领域中,因其生产成本低且具备和无机材料与金属材料同等的强度及功能性[2],故被更多领域所应用,其中具有代表性的即为建筑领域。建筑领域选取具备抗菌、防潮湿及保温等性能的高分子材料,用于建筑中能够提升住户的居住感受并有效降低能源消耗。因建筑高分子材料常年处于四季变化的高低温转换环境中,故对其热稳定性效果的分析至关重要。建筑高分子材料热稳定性是指其处于逐渐升温和受热的状况中时[3],其各种化学和物理性能的稳定性,属于检测耐高温材料的关键性能参数[4]。
有限元分析方法是指经过简化实物结构求得有限个数值,以此对实际环境的无数个未知量实现模拟的近似运算方法[5]。在建筑高分子材料的热稳定性检测中加入此方法,对材料受热状况中的各种物理、化学性能予以分析,能够更清晰地分析出材料的热稳定效果。因此,本文提出基于有限元的建筑高分子材料热稳定性效果分析,其结果能为节能型建筑中合理应用此材料奠定基础。
1 基于有限元的建筑高分子材料热稳定 性效果分析
1.1 原料选取
树脂混凝土属于一种建筑高分子材料,其关键组成有骨料、填料及粘结剂[6]。其中,本文选取兼具热力性能的高纯石英砂作为树脂混凝土的骨料,其二氧化硅纯度高达99.6%。以不同尺寸划分所选石英砂为七级,将其用作替换建筑用树脂混泥土内的粗石粗骨料与细砂细骨料;云母粉、石英粉、滑石粉及碳酸钙粉为常用的树脂混凝土填料,本文以云母粉为填料提升普通混凝土的韧性;出于对加工条件的考量,环氧树脂的粘性不易太高,故选取E50 牌号的环氧树脂,并以T30 和二缩水甘油醚分别作为与E50 共同使用的固化剂和稀释剂。
选取三种颗粒尺寸相连的石英砂为骨料,具体尺寸为:0.8mm~1.9mm、1.9mm~2.2mm、2.2mm~3.9mm。不同尺寸级别骨料的配比情况见表1。

表1 骨料的组成配比Table 1 Composition and proportion of aggregate
加入65g 云母粉填料,并根据比例将各级骨料共同减少65g;树脂粘结剂中环氧树脂、固化剂与稀释剂分别为38g、15g、12g。
1.2 待测性能及测试仪器
因本文将树脂混凝土材料作为建筑高分子材料进行分析,故该材料在受热情况下的抗弯曲强度、抗压性能及热膨胀性能等均比较重要[7]。
所用测试仪器包括:高分子材料电热测试机、山东铭高工业装备有限公司生产的ryg01 型号热压罐、北京中西远大科技有限公司生产的RFS10-DF-3000 型号火焰喷涂机及江苏大华激光科技开发有限公司生产的JSDH-4015GF 型号高分子材料切割仪器。
1.3 试样制备工艺
以1.2L 的塑料烧杯作为制备中的模具,为方便成型后脱模可提前在模具内铺好塑料保鲜膜。树脂混凝土试样制备工艺过程描述为:先以表1 中骨料配比为依据称量骨料,根据颗粒直径高低分别放入并均匀混合;再依次对环氧树脂、稀释剂与固化剂进行称量,按所需比例混合后为树脂粘结剂,放入骨料混合物内;另外按所需质量加入云母粉填料,共同混合搅拌;最后倒入模具内成型并予以手动捣实,在常温下放置36h 后固化成型,脱模后获得树脂混凝土试样。制备树脂混凝土试样的工艺过程如图1 所示。

图1 树脂混凝土试样制备工艺过程图Fig. 1 Technological process diagram of resin concrete sample preparation
运用高分子材料切割仪器将制备后的树脂混凝土试样切割为长方体试件,并对其热力学性能进行测试。
1.4 三维热力学模型
在单向拉伸的基础上提出树脂混凝土材料率相关和小变形的一维线性本构方程,可表示为:

式(1)中,弹性模量、粘性系数、热膨胀系数、延迟时间、蠕变残余应变以及形变量依次通过F、φ、β、γ、sω、δ表示,S表示温度。
基于粘弹性力学理论扩展一维热力学本构关系为三维,同时修改成热粘弹性本构模型中的UMAT 材料子程序,实现在应力多变状况下对树脂混凝土材料热力学性能的充分描述[8]。其过程为:如果不将式(1)内的蠕变残余应变与温度影响考虑在内,则所得粘弹性本构方程可表示为:

通过式(2)可得:

通过剪切模量H(t)和体积模量L(t)两个与时间有关的互为独立的系数描述树脂混凝土材料的力学行为。若树脂混凝土材料的体积变形属于线弹性,那么可得出:



修改式(5)为增量形式,其式为:

将热膨胀影响考虑在内,通过式(1)获取的本构关系增量形式可表示为:

在使用有限元实行数值模拟时,可设蠕变残余应变为常量,并为其取93%~94% 的卸载应变值。通过以上过程可得出可用在有限元分析的树脂混凝土材料热力学本构方程:

融合对理想流体力学行为与对理想弹性体力学行为分别进行描述的粘壶与弹簧,实现对树脂混凝土材料粘弹性现象的宏观描述[9-10]。串联一个粘壶和一个弹簧的模型即为Maxwell 模型,并联多个此模型和一个弹簧即为广义Maxwell 模型,此模型更适合用来描述松弛,对树脂混凝土材料力学行为的仿真可采用有限元软件材料库内可直接定义的广义Maxwell 模型实现[11]。通过线性粘弹性本构力学分析树脂混凝土材料的粘弹性,本构关系为:

粘性系数 和剪切模量之间的关系式为:

在材料粘弹性有限元运算时,需转换材料的剪切模量为通过Prony 级数表达的离散形式,其式为:
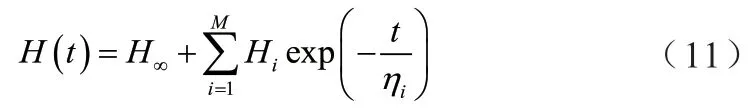
式(11)中,时间与松弛时间分别通过t和iη表示,原状态、时间无限大时的剪切松弛模量、各个时间的剪切松弛模量依次表示为H0、H∞、Hi。因使用Maxwell模型描述粘弹性,故材料在时间接近无限大时,已呈现出流体特征,也就是剪切松弛模量 0H∞= ,那么式(11)能够表示为:


通过有限元无法对所获得的材料松弛曲线直接进行分析运算,为实现在时间- 温度对数坐标系内将log bS值求得,应转换材料松弛曲线为通过Prony 级数拟合剪切模量的离散形式。通过将某温度下所获取的松弛曲线平移,得到各种温度下材料的松弛曲线,此即为材料的时温等效原理[12]。
通过时温等效关系创建(t′,S)或(t,S)间的联系,将独立变量的数量降低,达到简化粘弹性能检测的目的。同时,在各种温度下建立特定时间段的应力松弛曲线,并通过时温等效原理对各种温度下的数据进行平移,形成参考某个温度且可对众多时间数量级实现覆盖的一根组合曲线,减少检测时间[13-14]。树脂混凝土材料的移动因子logb(S)和(S-S0)间的联系可表示为:

式(13)中,材料常数以A1、A2表示,其单位同温度相同。
1.5 有限元模拟
通过有限元软件创建树脂混凝土有限元模型,模型的边界条件为:分别在X、Y、Z 等于0 上对x方向自由度、y方向自由度及z方向自由度进行约束。采用Hex单元形状、C3D8 单元类别实现网格划分。模型的尺寸是30mm×30mm×90mm。有限元模型如图2 所示。

图2 树脂混凝土有限元模型Fig. 2 Finite element model of resin concrete
通过向有限元软件内输入剪切松弛模量Prony 级数拟合系数,实现以广义Maxwell 模型模拟树脂混凝土热力学行为的目的[15]。
2 测试结果分析
以所制备的树脂混凝土试件为例,通过有限元软件从电-热-力性能与纤维体积含量对热稳定性影响两方面进行分析,得出所制备的建筑高分子材料- 树脂混凝土试件的热稳定性效果,具体过程如下。
2.1 树脂混凝土试件的电-热-力分析
从树脂混凝土有限元模型的一端分割出0.6mm 长的模型创建出30mm×30mm×0.6mm 尺寸的树脂混凝土试件三维模型作为应力场分析模型,如图3 所示。

图3 试件应力场分析模型Fig. 3 Stress field analysis model of specimen
以高分子材料电热测试机采集试件电热荷载信息,分别为试件施加3A、5A、7A 电流,测试三种电流作用下试件表层ef 中线上的热应力变化情况。测试结果如图4 所示。

图4 不同电流作用下试件的热应力变化情况Fig. 4 Variation of thermal stress of specimen under different electric current
通过图4 可得出,在电流强度升高的情况下,树脂混凝土试件的热应力也随其升高,且不同电流强度下的试件热应力变化趋势相近,可见本文树脂混凝土试件的热膨胀阻碍效果明显,且热应力性能表现稳定。
将X=15mm 处的电流与热应力变化情况单独呈现,图5 所示。
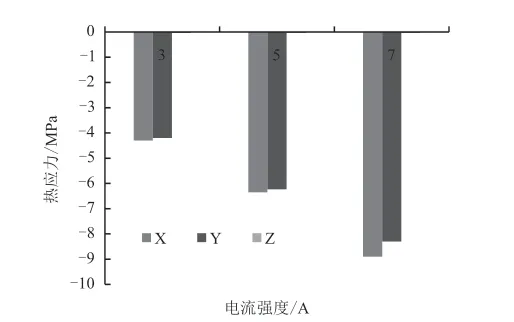
图5 X=15mm 处的电流与热应力变化情况Fig. 5 Variation of current and thermal stress at X =15mm
由图5 能够更清晰地看出,Z 轴方向上的热应力近似于0,且几乎无波动,X、Y 两轴方向上的热应力变化较为明显,热应力和电流处于一种正比关系,由此可见,实验试件的X、Y 轴方向对热膨胀的阻碍更显著,热稳定性效果更好。
2.2 纤维体积含量对热稳定性的影响分析
为检验树脂混凝土试件制备中纤维体积含量不同对其热稳定性的影响,现对树脂混凝土试件中包含10%、20%、30% 三种不同纤维体积含量时试件的应力- 应变关系进行检测,试件检测处于-20℃~60℃的升温环境中,检测结果见表2。

表2 应力-应变关系检测结果Table 2 Test results of stress-strain relationship
由表2 可得知,在同样的升温环境中,试件的纤维体积含量的提升对树脂混凝土材料的热力学性能的影响可通过应力- 应变关系反映出,当达到同等应变时,纤维体积含量越高所产生的内应力越高。
继续检测在升温环境中不同纤维体积含量试件的等效拉伸模量和温度间的变化关系,检测结果如图6 所示。

图6 等效拉伸模量与温度变化关系Fig. 6 Relationship between equivalent tensile modulus and temperature
通过图6 能够得出,同等温度条件下试件的纤维体积含量越高其等效拉伸模量越高,随着温度的升高不同纤维体积含量试件的等效拉伸模量均轻微下降,而含量越高的试件下降趋势越轻微,可见,树脂混凝土材料的纤维体积含量直接影响其热稳定性能,二者呈正比关系。
3 结论
本文提出基于有限元的建筑高分子材料热稳定性效果分析,有限元法是指通过分割物理结构为数个区域,每个区域为一单元,并以节点连接各个单元,同时融合所创建的各单元作用力方程为整体结构的系统方程,对其运算后获取结构近似解的过程,其所用的通用分析软件为有限元软件,具备线性静态分析与繁琐的非线性动态分析等多种分析性能,分析方向有压电分析、热分析与结构分析等。本文以树脂混凝土为例,通过有限元分析方法对其试件的热稳定性效果进行分析,分析结果表明此试件的热膨胀阻碍效果好,热应力性能稳定,热稳定性效果受其纤维体积含量高低影响。在未来的研究中会继续针对建筑高分子材料中的其它材料实行分析,充分验证建筑高分子材料的热稳定性能,为节能型建筑合理应用此种材料降低能耗提供科学依据。

