基于知识维度的高考复数试题评析

彭艳贵,徐 伟,刘 兵,王鹤颖

(1.鞍山师范学院 数学与信息科学学院，辽宁 鞍山 114007；2.东北师范大学 数学与统计学院，吉林 长春 130024；3.鞍山师范学院附属中学，辽宁 鞍山 114007)

复数理论是数学学科的一个重要分支，随着我国基础教育改革的进行，高中复数的课程内容在社会的争议中被逐渐删减.2000年之前的高中数学教学大纲中，复数内容设置基本维持在16课时以上，但在2002年版的教学大纲和2003年版的《普通高中数学课程标准(实验)》(以下简称为“课程标准”)中复数内容设置仅为4课时，与以往详细的复数课程体系相比，这一阶段实施的高中复数课程既不难也不多，在一些师生看来，复数部分似乎已经无关紧要，成为高中数学中最容易忽视的一部分.在高中数学课程“削枝强干”理念下，产生了削枝如何保证强干、如何才能通过复数课程体现数系扩充的目标、如何突出核心概念的理解与掌握等问题，这些问题在任何一个知识主题下都值得思考.根据我国基础教育发展需求，高考作为一种普遍的教育评价方式，在知识的广度意义下可以为相关课程及教学评价研究提供依据.

知识维度是高中数学学习的一个重要方面，2003年版课程标准是过去十几年教学实践的基础，明确了高中复数学习目标为四个方面：“理解引入复数的必要性”“了解数系的扩充”“掌握复数的表示、运算”“复数的几何意义”[1].教育部组织专家在2017年对课程标准进行修订并于2018年发布，目前尚处于初步推广阶段，经过对课程标准文本的比较，可以发现这两个版本课程标准中复数内容的必修部分基本保持一致，但2017年版课程标准中增加了复数的三角表示作为选修内容，反映了专家和学者认为高中复数内容体系需要强化的一种倾向.在课程发展的众多影响因素中，复数试题的知识维度的评价情况是反映复数课程核心要求的一个最基本方面，通过分析高考复数试题的知识维度考查情况，对高中复数课程发展及考试评价等方面的研究具有重要意义.因此，本文围绕以下两点进行分析：第一，2009—2018是现有高中复数课程实施的稳定阶段，对高中复数课程实施具有较好的阶段代表性，所以，本文对这十年高考复数试题进行统计并研究知识点分布，从知识的广度意义分析高考复数试题；第二，借助描述统计方法分析十年中的复数知识点考查倾向性，分析课程标准中“体现数系扩充”这一教学目标的具体表现.通过以上两个方面的研究，在一定程度上能够反映出特定阶段高考复数命题的内容、形式等方面的信息.

1 研究思路与方法设计

1.1 样本选择

多数高考数学试卷只包含一道复数题目，个别试卷不包含复数题目，因此，一套高考数学试卷并不足以反映高考中复数知识考查的倾向性.本研究选择某一个阶段的高考复数试题进行讨论分析[2].自2003年版课程标准实施以来，经过一定时间的推广与实践，2009—2018年间可以认为是课程标准及配套教材实施的相对稳定阶段.高考数学试卷的范围包括全国卷和上海、北京、江苏、浙江、山东、天津、福建、江西、安徽、重庆、辽宁、湖南、湖北、广东、四川、陕西、宁夏、海南等省市的文、理科试卷，共计243套试卷的208道复数题目.

1.2 理论框架与方法设计

本研究主要采用知识点比较的方式进行分析.复数知识点的概念界定参照已有研究的结果，是指课程标准中复数部分明确提到的相对较单一的复数知识系统，一般不再对课程标准中明确提出的单个复数知识性的定义进行细节性的划分[2].按照课程标准的内容表述，高中复数的知识点主要包括：复数概念、复数相等、复数的代数表示、复数代数表示的几何意义、复数代数表示的四则运算、复数代数表示加减运算的几何意义、复数与方程等.复数的模、共轭复数、复数与其他知识主题相结合等知识点，虽然在课程标准中没有直接提及，但在人教版等高中数学教科书和高考题目中，按照知识的邻近拓展原则，也应该包括进去.

首先，统计每年的高考数学试卷中的复数题目数量，确定这些复数题目中包含的复数知识点，从复数知识分布的广度意义上进行分析.其次，由于每年高考全国卷、省市卷的动态变化，使得每年的高考复数题目数不同，所以不能简单地用知识点计数的方式比较高考复数试题的考查情况.将包含某个复数知识点的题目数量占当年复数题目总数进行百分比转换，再对其进行比较，用描述统计方法分析复数知识点的考查倾向性.

2 统计结果与分析

统计的高考试卷中，2009年上海(文科)试卷和2011年上海试卷(文理复数题目相同)各为一道复数解答题，2012年上海试卷(不分文理)包含两道复数题目：一道填空题和一道选择题，除此之外，所选择的每套试卷均包含一道复数题目，题目的形式为选择题或填空题.统计并整理试题中的复数知识点与数量分布，基本统计数据如表1所示.

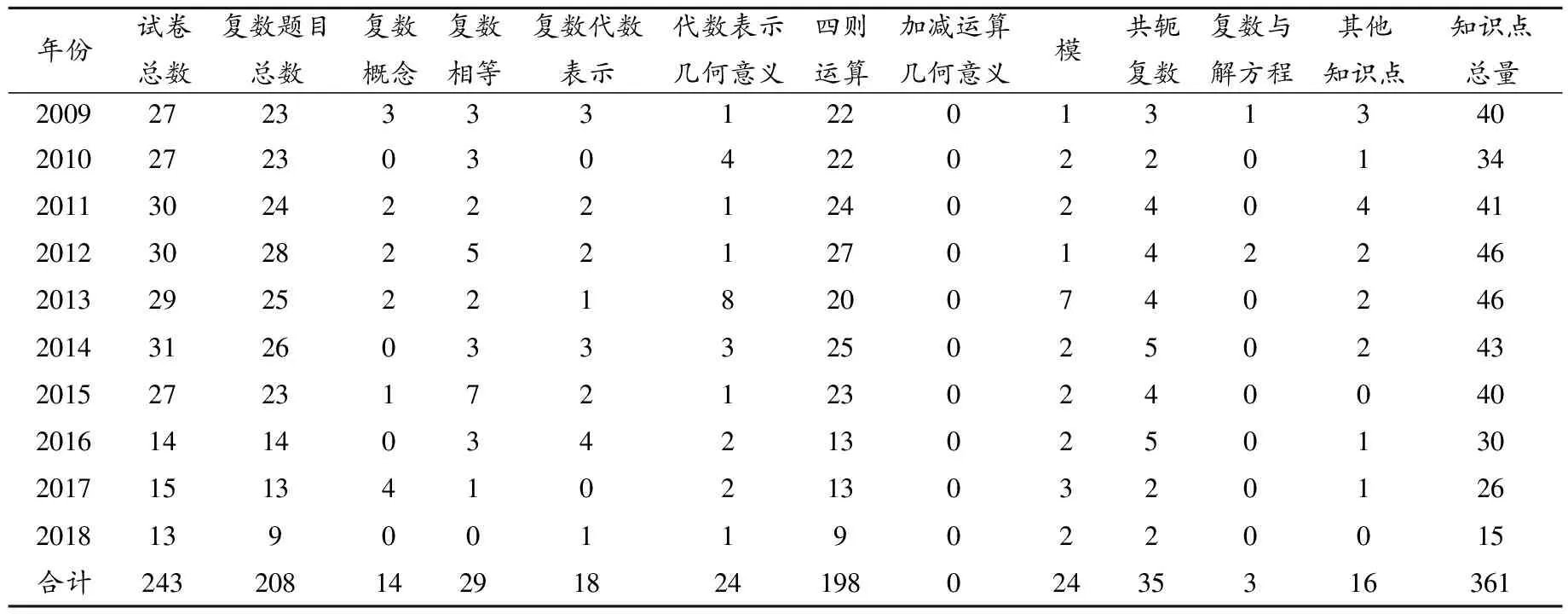
表1 高考试题复数知识点数量分布结果

整理并统计2009—2018年间的高考复数试题，目的是在广度意义下分析高考的评价形式中复数知识点的分布状况及复数内容考查的整体变化趋势.由于全国卷的适用范围和省市自主命题的范围动态变化，每年高考试卷中复数题目数也不同，所以在上述数据表的基础上，进一步统计包含某个知识点的题目数占当年总题目数的比值，如2013年有2道题目考查复数概念，当年复数题目总数为25，占比为8%.详见表2.

表2 考查单个知识点的题目数占比 (%)

从统计结果可以看出，高考中复数知识点的考查范围主要包括：复数概念、复数相等、复数的代数表示、复数代数表示的几何意义、复数代数表示的四则运算、复数与方程、复数的模、共轭复数，以及复数与其他知识主题的结合，共9个知识点，而课程标准中要求的复数加减法几何意义这一知识点在复数试题中没有直接出现.值得注意的是，这些试题中复数的四则运算是重点考查的知识点，复数与方程的试题仅在2009和2012两个年度高考试卷中出现.比较来说，在这十年的高考复数试题中，复数概念、复数相等、复数代数表示、代数表示的几何意义、模、共轭复数、与复数关联的其他知识点的考查也存在一定程度的倾向性.

3 讨论与启示

3.1 复数知识点的考查明显集中在复数代数表示的四则运算

对2009—2018年的高考数学试题分析发现，包含复数代数表示四则运算知识点的题目数占比复数题目总数量中，2013年的比值最低，为80%，其余年份考查复数四则运算的题目均占到90%以上.2003年版的课程标准中，对复数代数表示四则运算的要求是“能进行复数代数表示的四则运算”，课程标准中行为动词“能”对应“知识与技能”目标领域的理解水平，即是在中等认知水平的要求下学习复数代数表示的四则运算，对任意两个代数表示的复数进行加、减、乘、除四则运算.2017年版的课程标准中，对复数运算的要求是“掌握复数代数表示的四则运算”，对这部分认知水平的要求程度有所提高.高考试题也很大程度侧重于考查复数的四则运算，但从高考题目来看，很多的运算题目都属于基本的操作运算，属于较低水平的认知要求，在揭示复数作为数的特征及相关方面表现并不明显.有学者描述数学学习的一种现象是“一看就会，一做就对”，用来形容高中生在复数方面的一些表现再恰当不过，但这并不表明学生真正学会了复数、理解了复数，只是说明低水平要求下，学生在复数代数表示方面可以形式化地学习相关内容，但还需要深入掌握运算的意义和方法等.一方面，在数系扩充理论中，复数系要满足数系扩充前的实数系的各种运算法则；另一方面，在数系的扩充理论中，复数系还要体现出与实数系不同的运算特征，即开方运算的封闭性.这两点是数系扩充理论中在运算意义下体现数系扩充合理性和必要性的两个基本方面.通过分析高考复数题目发现，复数代数表示的四则运算仅是最基本的加、减、乘、除四则运算，没有表现复数运算特征的开方运算，虽然个别题目中包含i2=-1这样的内容，但在思维形式和运算一般性方面都不足以体现复数开方运算的特征，更不足以体现在运算方面引入复数的必要性.

3.2 复数几何意义的知识点考查较少

复数几何意义是复数理论的重要内容，对复数几何意义理解不足将影响学生对运算的深入理解，不利于复数理论的展开.按照课程标准要求，高中复数只要求复数代数表示，无论在复数的定义形式方面，还是在复数的几何意义方面都显得十分单一.在教与学的过程中对复数几何意义的认识局限在“复数代数表示与复平面上的点之间一一对应”.在复数发展历史上，复数的几何解释具有重要地位，这是复数被广泛接受的直接原因.按照弗赖登塔尔的“再创造”原则，高中复数的课程内容和考试评价等方面体现复数几何意义的有关内容是积极且必要的，不仅需要“复数代数表示与复平面上点之间的一一对应”，而且要了解复数运算的几何意义，尤其是能够体现复数本质特征运算的几何意义.

3.3 复数知识点的考查比较单一

调查结果表明，多数高考复数题目的知识点考查比较单一、孤立，不强调知识的深入理解，对学生学习复数知识的过程性体现不够.如果考试强调的是复数知识的琐碎方面，容易被看成是对不连贯教学和机械学习的鼓励，这对高中复数课程的发展是非常不利的.由于课程改革过程中高中复数内容逐渐减少，仅局限于概念、法则等内容的形式化的学习，难以体现高中复数内容学习的必要性.比如，在复数代数表示及几何意义学习过程中，学生很容易把实部和虚部看成独立的两个部分，而不是一个完整的数，把复数运算看成是实部和虚部两个部分单独的实数运算；或者，把实部和虚部组成的数对完全等同于坐标，抑或把复数混淆于向量，这对复数本质的理解、复数运算几何意义的掌握是非常不利的[3].复数的理解过程对应表象的建立过程，复数概念的理解随着表象的不断修正而不断完善.高考复数试题的考查应关注过程性的考查，避免师生在复数学习过程中产生理解偏差.

3.4 在复数范围内求解方程的相关要求较弱

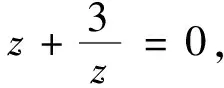
3.5 复数试题的知识维度与课程标准存在一定程度的“不一致”

在课程标准中，明确提到的复数内容包括：“复数的四则运算”“通过方程认识复数”“复数概念”“复数相等”“复数代数表示的几何意义”“复数加减法的几何意义”.复数试题的考查一般仅达到了课程标准要求的较低限度.课程标准中复数代数形式四则运算的认知要求属于理解水平，有的题目的复数运算知识按照运算法则进行简单的加法或乘法运算，如2018年全国二卷中的一道复数题目是计算i(2+3i).所有复数试题中没有对“复数代数表示加减运算的几何意义”这一知识点的考查.还有一些内容超出课程标准和考试大纲的范围[4].“复数的模”和“共轭复数”虽然没有在课程标准中明确提到，但是有一定数量的题目包含这两个知识.间接说明这两个知识点在复数有关内容的理解中是比较核心的内容，作为复数运算和复数几何意义的重要支撑概念，应该得以强化.按照古德莱德(Goodlad)的课程层次理论，这在一定程度上反映了“运作课程”与“经验课程”表现出来的目标性，以及它们与“正式课程”之间的形式不一致性和拓展关联性.

3.6 考查复数与其他知识点联系的内容较少

复数在联系不同数学知识主题和不同学科内容方面具有独到之处，如复数可以联系指数函数与三角函数这两个没有什么直接关系的函数，可以联系数学与物理两个学科之间的知识内容.加强复数与其他知识的联系应该是高中复数教育价值的一种体现.但这十年的高考复数试题中，复数以外知识主题的题目总体不多，主要包括：真假命题、命题的充要条件、集合运算、不等式、轴对称变换、中心对称变换等，直接原因是课程标准对复数内容的定位和要求本身就属于比较基本的水平，普通课程标准对一些复数知识的要求是了解或认识、感受或体会等，形式上按照一定的程序或步骤模仿便可实现，在知识的教学和学习深度上没有过多要求.

从复数的出现到复数理论系统的完善过程中，复数一直与其他数学知识或者物理等其他学科有着广泛的联系，是解决其他学科或实际问题的重要工具.欧拉、高斯等数学家研究发现了复数与其他知识主题的广泛联系性和普遍应用性，如欧拉的复数理论研究把复数与指数函数、三角函数统一在一起.高斯、维塞尔等人给出的复数几何解释让人们在普遍接受和认可复数的同时，也为平面几何问题求解提供了复数方法.建立复数与其他知识主题的广泛联系，有助于学生对复数内容的认识和理解.复数具有多种表示形式，每一种表示形式都能够反映复数的不同特征、对应不同的几何解释形式.因此，强化复数的表示形式，是实现复数与其他知识主题关联的有效切入点.心理学研究表明，呈现多种复数表示形式有利于学生在思维层次上关联其他知识主题，形成正确的心理表征，实现对概念的深入理解.复数的代数形式在表现实数系到复数系的扩充方面的意义是明显的，复数的代数表示也很容易被学生在形式上接受，学生也习惯于类比实数范围内的多项式运算来学习复数四则运算，这样还能够体现出复数与之前知识的关联，以及复数系与扩充前的数系运算的一致性.复数的三角表示是与其他知识主题联系的纽带，是复数理论展开的重要支点.复数的三角表示部分包含复数的模、辐角等内容在复数几何意义方面是必不可少的，初等数学中这些内容紧密联系伸缩变换、旋转变换等几何变换.这些内容与高等数学有着紧密联系，是学生今后继续学习高等数学的基础.

4 结语

泰勒从课程发展的角度，提出教学目标的确定既要符合进步主义观强调学生发展需求，也要符合要素主义观筛选基本知识的观点[5].这种主张指明：在高中复数课程的思考中，综合学生个体的发展需要和知识结构的要素是基本的要求.实际上，不同版本的课程标准对高中复数地位均表现出较为积极的认可，一致强调复数的重要性，认为复数是一类重要的运算对象，有广泛的应用，要求学生理解引入复数的必要性，了解数系的扩充，掌握复数的表示、运算及其几何意义[6].但是在高中复数课程的具体表现方式、知识体系的设置、课时数量等方面存在着对课程的重要性表现不充分的矛盾，尤其是在高考复数试题的考查表现上倾向明显.从研究的总体上，高考复数内容的考查以复数代数表示的四则运算为主，从数系的结构和要求上，强调数集上定义的运算符合课程标准中的数系扩充的课程目标.但为了学生的后续学习，高考中关于复数内容的评价应该紧密结合课程目标的要求，为学生的终身发展服务，实现复数的评价与课程的一致性，在此基础上检验“四基”“四能”等方面的目标要求.在教学评价的意义上，高考考查的内容首先要确定以学生学习目标为导向的目标要求，其次要进行教学内容的整合[7].在内容的组织上，不仅体现对具体复数知识点的考查，更要在客观上体现对一般原理的渗透与揭示，给学生在思考问题的同时以深刻的启示，正如张奠宙先生在高中复数内容方面的主张：内容要更新，但基础决不能削弱[8].因此，在今后的课程研究中有必要进一步研究高中复数的评价与课程的发展、设计等方面的内容.