我国消费价格指数的走势预测及影响因素分析

（平顶山学院 数学与统计学院，河南 平顶山 467000）

一、引言

居民消费价格指数是一种能够反映人们家庭日常生活所消费的产品及服务的重要物价变动指标。通常，CPI的增幅可以用来界定通货膨胀的严重程度，临界点一般为3%和5%。当发生通货膨胀时，一般对应CPI的增长幅度会大于3%，当CPI出现大于5%的增长幅度时，我们会认定发生了严重的通货膨胀。

当CPI的增长幅度反映出我国具有通货膨胀的倾向时，央行将实行紧缩的货币政策和财政政策，这一宏观调控从长远看并不利于经济的稳定发展。因此，加大对该指数的研究和预测对于稳定经济、把握经济运行的规律以及宏观调控的方向有重要意义。

石捡情和杨世娟（2017）选取2009年1月至2017年4月的CPI时间序列数据，采用时间序列分析的方法，对数据进行处理及ADF检验来分析CPI序列的特征，并选择自回归移动平均（ARIMA）模型对我国的居民消费价格指数数据进行建模预测，得出2017年5月CPI指数为101.8%，预计通货膨胀温和[1]。魏静洁（2016）通过选取1990—2014年我国CPI数据，运用单因素分析求和和多元线性回归模型相结合的方法，既可以看出各个因素对我国居民消费价格指数的影响程度，又可以得出各个影响因素和被解释变量之间的模型表达式[2]。杨坚和费俊俊（2014）基于ARMA模型基础，实证分析了我国国内物价水平的总体走势和居民消费价格指数与社会经济发展相联系的变动规律，并根据所建立的模型进行了预测，得出ARIMA模型对居民消费价格指数的数据拟合很好[3]。

二、相关模型

1.ARIMA模型简介

ARMA移动平均自回归模型[4][5]（Autoregressive Moving Average Model），是一类常用的随机时间序列分析模型。ARIMA模型相对ARMA模型，多了差分操作。

具有如下结构的模型称为求和自回归移动平均模型，简记为 ARIMA（p，d，q）模型：

由上式可以看出，模型的实质就是差分运算与模型的组合。

当 d＝0 时，ARIMA（p，d，q）模型实际上就是 ARMA（p，q）模型。

当 p＝0 时，ARIMA（0，d，q）模型可以简记为 IMA（d，q）模型。

当 q＝0 时，ARIMA（p，d，0）模型可以简记为 ARI（p，d）模型。

ARIMA（p，d，q）模型可以对具有季节效应的序列建模。根据季节效应提取的难易程度，可以分为简单季节模型和乘积季节模型。

表1 不同模型的ACF和PACF特征

简单季节模型的产生是由于序列之间的季节效应和其他效应之间存在加法关系，这时，各种效应信息的提取都非常容易，通常简单的周期步长差分即可将序列中的季节信息提取充分。简单季节模型实际上就是通过趋势差分、季节差分将序列转化为平稳序列，再对其进行拟合[6][7][8]。模型结构通常如下：

式中：D为周期步长，d为提取趋势信息所用的差分阶数；εt｛｝为白噪声序列，且Θ（B）=1-θ1B-…-θqBq为 q 阶移动平均系数多项式；Φ（B）=1-φ1B-…-φpBp为p阶自回归系数多项式。

通常而言，由于简单的季节模型并不足以提取序列间的长期趋势效应和随机波动等交互影响关系，因此才产生了季节乘积模型。乘积模型的构造原理如下：

低阶 ARIMA（p，d，q）模型用来提取序列的短期相关性。而当序列具有季节效应，季节效应本身还具有相关性时，季节相关性可以使用以周期步长为单位的ARIMA（p，d，q）模型提取。

乘积模型简记为 ARIMA（p，d，q）×（P，D，Q）S，综合前面的d阶趋势差分和D阶以周期S为步长的季节差分运算，对原观察值序列拟合的乘积模型完整的结构如下：

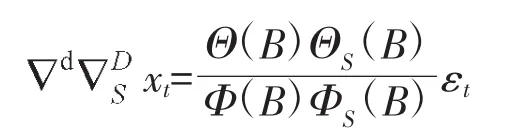
式中：

Θ（B）=1-θ1B-…-θqBq

Φ（B）=1-φ1B-…-φpBp

ΘS（B）=1-φ1BS-…-φQBQS

ΦS（B）=1-φ1BS-…-φpBPS

2.主成分回归

主成分分析是针对多个解释变量，将关系紧密的变量剔除，建立尽可能少的新变量，使这些新变量两两不相关。也就是说，把原来的多个变量重新组合成几个能充分反映总体信息的新变量，新组合的变量之间是相互独立的，而且这些新变量在解释因变量时尽可能保持原有的信息，从而在不丢掉重要信息的前提下消除变量间的共线性问题，便于进一步分析。基本步骤如下：

（1）原始数据标准化。由于原始数据的单位之间存在差异，为了消除各个经济指标在量纲和数量级上的差别，首先对数据进行标准化处理。

（2）计算相关系数矩阵。根据标准化数据建立协方差矩阵R。R是反映标准化之后的数据之间相关关系密切程度的统计指标，值越大，说明越有必要对数据进行主成分分析。

（3）求相关矩阵R的特征根、特征向量和方差贡献率，确定主成分个数。特征值是各主成分的方差，其大小反映了各个主成分的影响力。主成分Z1的贡献率，累计贡献率为。主成分个数的选取原则为特征值大于1且累计贡献率达80%—95%。

（4）计算主成分得分，其得分是相应的因子得分乘以相应方差的算术平方根。

（5）使用主成分代替原始变量与Y建立多元线性回归模型。

三、CPI走势预测结果分析

1.数据获取

研究使用的数据为我国居民消费价格指数，样本区间为2001年1月至2017年12月，数据来自国家统计局官网。

2.模型建立与预测

建立模型之前需要先验证原始序列的平稳性。利用R软件画出序列CPI的时序图，并判断其平稳性，如图1所示。

根据图1，可初步认为CPI序列是平稳的。为了避免判断的主观性，对序列进行单位根检验，进一步确定序列的平稳性，如表1所示。

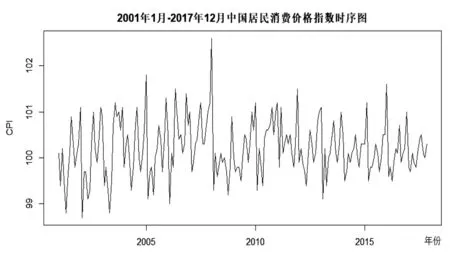
图1 2001年1月至2017年12月中国居民消费价格指数时序图

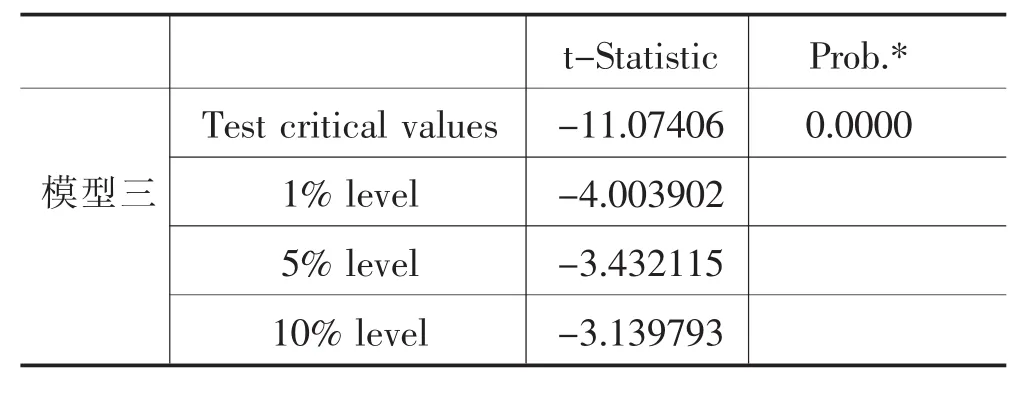
表2 ADF检验结果

上述模型，原假设为存在单位根，序列不平稳；备择假设为不存在单位根，序列平稳。

模型三的t-Statistic值为-11.07406，小于三个测试临界值并且p值显著小于0.05，因此拒绝原假设，表明我国2001—2017年居民消费价格指数序列不存在单位根，序列具有平稳性，可继续进行白噪声检验。

表3 原始序列白噪声检验

白噪声检验的假设条件为：

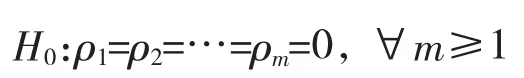
H1：至少存在某个

延迟6阶的LB统计量p-value＝0.01939，延迟12阶的LB统计量p-value＝1.051e-09，统计量的p值远远小于0.05，即拒绝序列为纯随机序列的假定，该平稳序列属于非白噪声序列，可以对其继续研究。

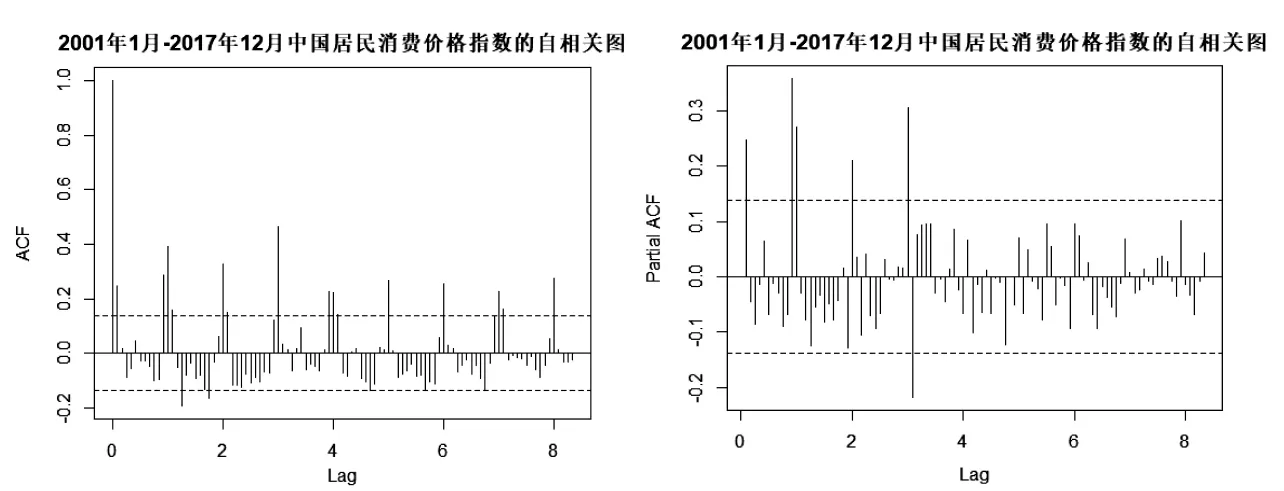
图2 2001年1月至2017年12月中国居民消费价格指数原始序列的自相关图和偏自相关图

从图2可以看出，原始序列的偏自相关图是截尾的，而自相关图以12为周期长度呈现出一定的周期性，因此，应建立季节模型进行进一步分析。

在建立季节模型之前对原始序列进行1阶12步差分来消除季节效应。

接着，利用R语言软件对不含有季节效应和趋势的序列进行系统定阶，可得系统定阶模型ARIMA（1，0，0）（2，1，0）[12]，其中：p＝1，P＝2，D＝1，d=q=Q＝0。

表4 系统定阶模型系数表

模型拟合输出结果，可以得到乘积季节模型ARIMA（1，0，0）（2，1，0）[12]的拟合模型为：

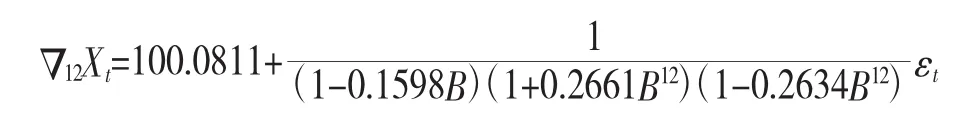
表5 残差白噪声检验结果

由残差白噪声检验结果可以看出，延迟6阶的检验p值为0.5565。在显著性水平α为0.05的条件下，由于概率p值远大于显著性水平0.05，所以要接受原假设，可以认为乘积季节模型提取的数据信息较为充分，该模型的拟合效果较为理想。

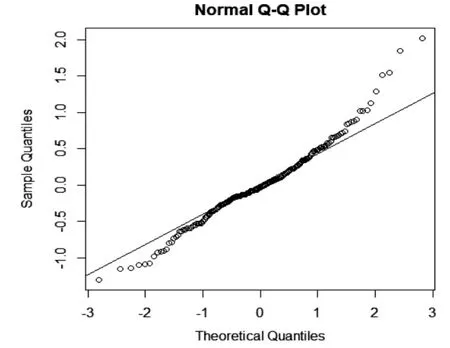
图3 正态检验Q-Q图

图4 残差分布图

由图3、图4可以直观地看出残差是随机的，残差基本服从正态分布，模型是有效的。

预测结果是以1995—2017年的CPI数据为样本，利用系统定阶模型 ARIMA（1，0，0）（2，1，0）[12]对 CPI序列在2018—2019年度的走势进行预测，得出预测结果列。

通过R语言拟合出的系统定阶模型ARIMA（1，0，0）（2，1，0）[12]绘制 2018—2019 年 CPI走势的预测图，以更加直观地感受CPI的变动趋势。

图5 预测图

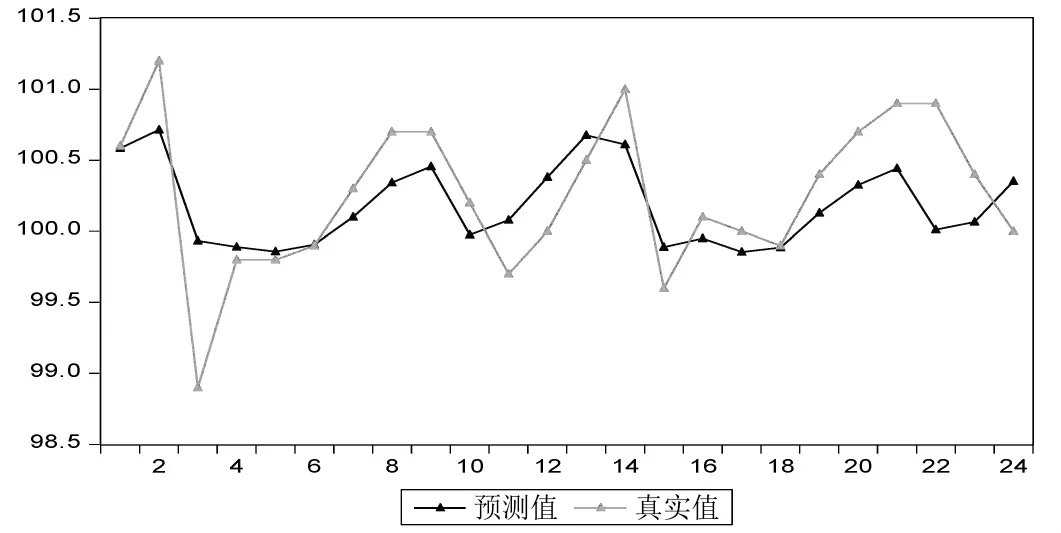
图6 预测结果对比图

表6 预测结果对比表

根据2018年1月至2019年12月的预测值与真实值求得相对误差：

相对误差＝（预测值-真实值）/真实值×100%

将相对误差取绝对值之后求得平均误差为0.33%，一般认为将平均误差控制在5%以内，模型预测效果较好。此处平均误差为0.33%，结合图5和图6我们可以非常直观的得出结论：ARIMA（1，0，0）（2，1，0）[12]模型的预测效果比较可观。

四、CPI影响因素结果分析

1.变量的选择及数据处理

在影响CPI的众多影响因素中，选取全社会固定资产投资（亿元）、人民币对美元汇率（美元＝100）、社会消费品零售总额（亿元）、工业生产者出厂价格指数（上年 ＝100）、货币和准货币（M2）供应量（亿元）、进出口总额（亿元）、GDP（亿元）和外汇储备等8个主要因素为自变量。

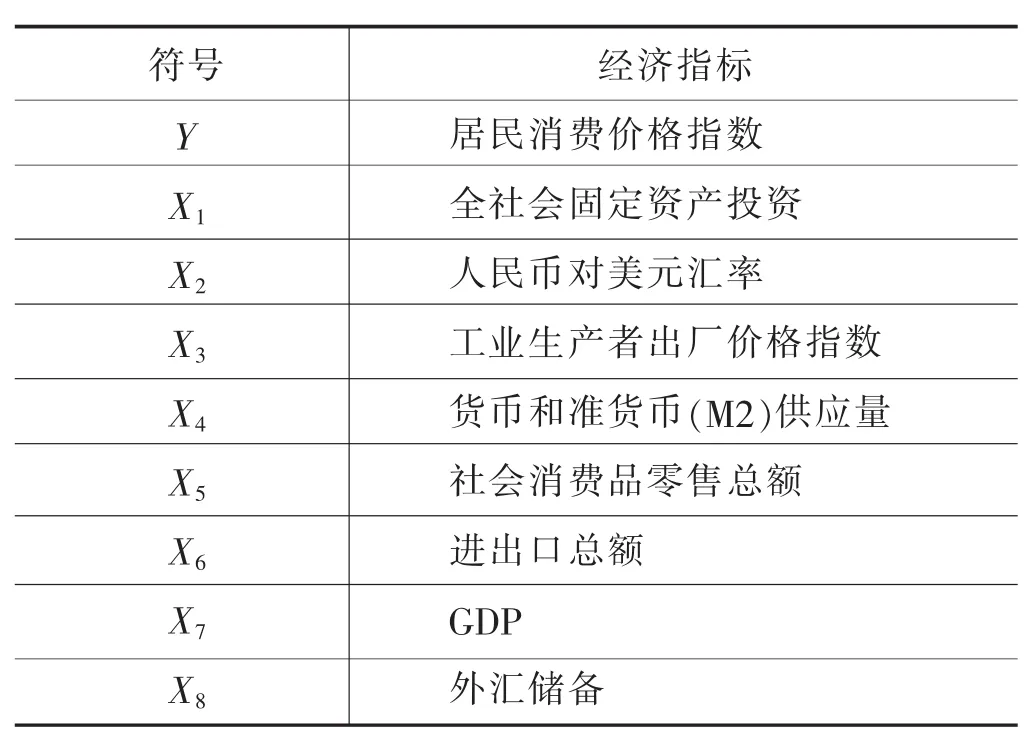
表7 符号说明

收集1995—2019年CPI及影响CPI变动的全社会固定资产投资（亿元）、人民币对美元汇率（美元＝100）、社会消费品零售总额（亿元）、工业生产者出厂价格指数（上年＝100）、货币和准货币（M2）供应量（亿元）、进出口总额（人民币）（亿元）、GDP（亿元）以及外汇储备8个指标的年度数据。其数据均来自国家统计局官网。

为了克服数据在整个值域中处于不同区间的差异带来的影响，将原始数据取对数处理，得到新的变量：ln（Y），ln（X1），ln（X2），…，ln（X8）。

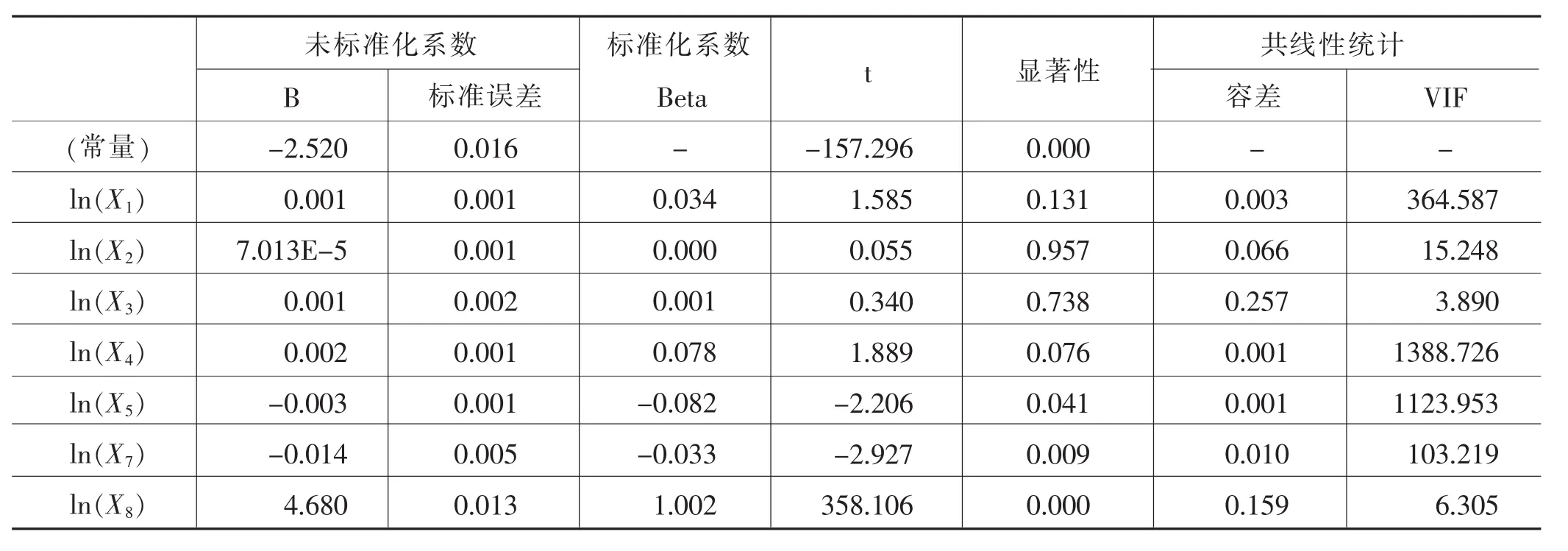
表8 模型系数表

变量间是否存在多重共线性，可以通过容忍度和VIF 值来判断。ln（X3）、ln（X8）的容忍度大于 0.1，加之 ln（X1）、ln（X4）、ln（X5） 的 VIF 值为 364.587、1388.726、1123.953，因此可以确定自变量之间存在严重的多重共线性。此处选用主成分回归方法来消除共线性的问题。

2.主成分回归模型建立

进行KMO检验和巴特利球体检验时，一般而言，KMO值大于0.5意味着因子分析可以进行，而在0.7以上则是令人满意的值。KMO值为0.711，最后一行数据sig值小于0.005，符合标准，各个变量的相关性合理，可以进行因子分析。

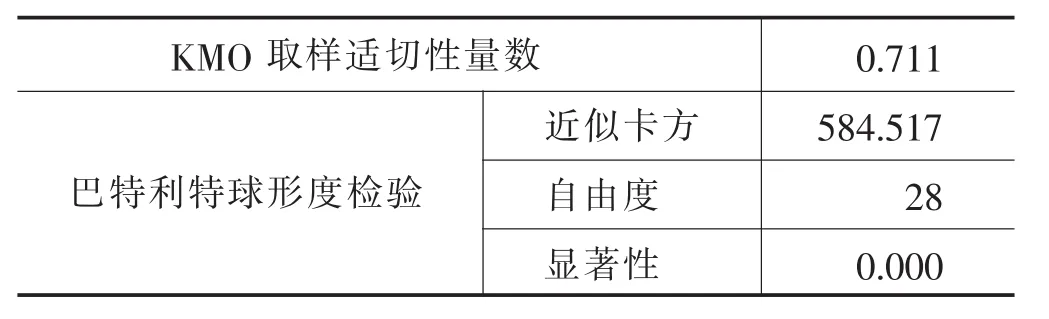
表9 KMO和巴特利特检验

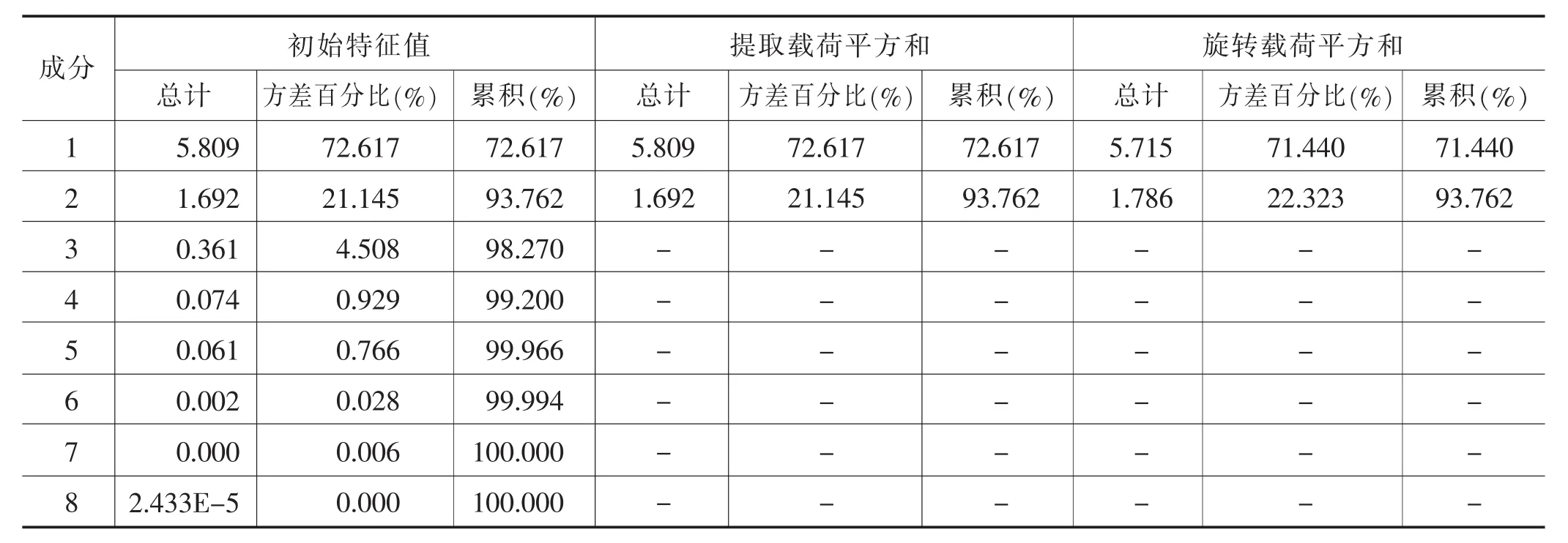
表10 总方差解释

表10第一列为8个成分，第二列为对应的特征值，第三列为主成分贡献率，第四列为累计贡献率。通常SPSS会默认选择将特征值大于1的成分作为主成分。从表中可以得出：成分1和成分2的特征值分别为5.809、1.692，明显特征值大于1；从累计贡献率来看这两个成分可以解释方差的93.762%，即主成分1和主成分2可以解释原来8个自变量93.762%的信息，因此抓住主要矛盾，提取两个主成分。

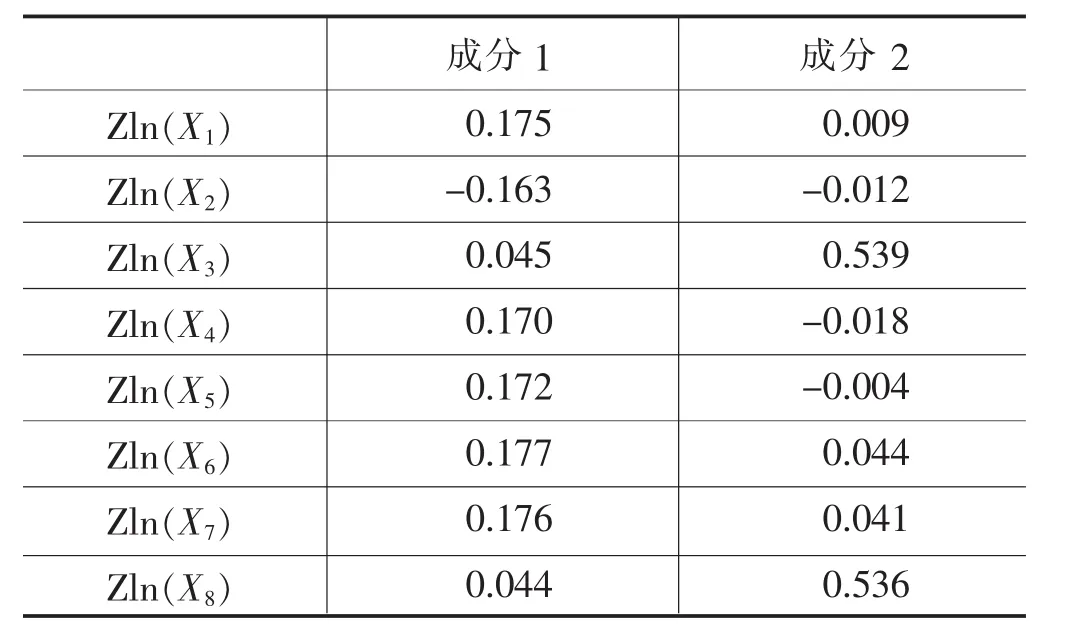
表11 成分得分系数矩阵

成分得分系数矩阵（表11）列出了各主要成分解析表达式中的标准化变量的系数向量，可以得出各主成分解析表达式分别为：

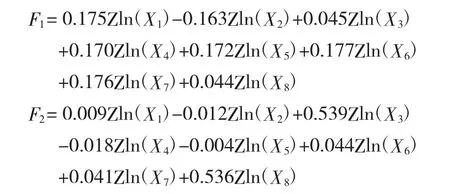
式中 Zln（X1）…Zln（X8）不同于 ln（X1）…ln（X2），而是标准化之后的变量。

用相应的因子得分乘以相应方差的算术平方根得到主成分得分 F1、F2，并且以 F1、F2为自变量，以标准化之后的ln（Y）为因变量建立回归模型。

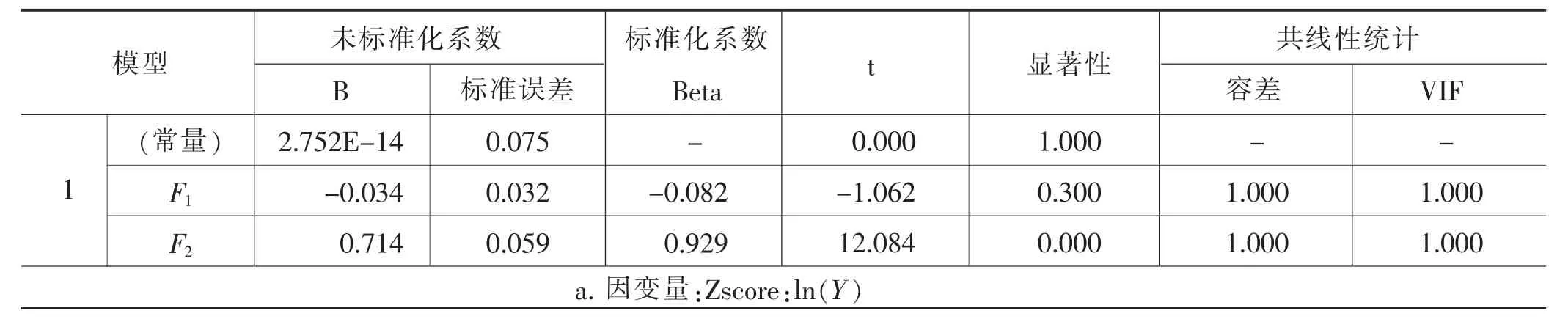
表12 系数表

此时变量F1、F2的VIF都显著小于10，模型不存在多重共线性问题，可以根据更改后的模型系数表，确定各个自变量的系数，得出主成分回归模型。

主成分回归表达式为：Zln（Y）＝-0.034F1+0.714F2

五、结果分析

为了保持物价稳定，减少物价大幅波动，维持我国居民消费价格指数相对稳定，给出以下建议：

1.维持汇率稳定

维持物价、汇率稳定，是各国宏观经济调控的核心内容。汇率稳定与物价稳定相辅相成，国家应从供给与需求两方面进行宏观调控，最大限度减少汇率的波动。

2.大力发展农业生产

既要进一步深化农业供给侧结构性改革，调整农业、畜牧业、渔业、林业的产业结构和产品结构，提升生态农产品、绿色农产品和品牌农产品的比重，又要坚持保供给、保收入、保生态协调统一，促进农民增收。要重点加强科技研发推广，提高绿色农业发展水平。

3.实施积极的财政政策和稳健的货币政策

一方面，把积极的财政政策的重点放在基本物资的保障供给上，合理地引导地方政府处理经济发展与通货膨胀之间的矛盾。另一方面，努力探索货币政策工具的创新，健全货币的决策机制，使我国的经济调节机制更加灵活，更加适应我国国情。◆