考虑任务优先级的超冗余机械臂避障轨迹优化
王 娜,商 丽,孙 军
(1.沈阳城市建设学院交通与机械工程系,辽宁 沈阳 110167;2.沈阳建筑大学机械工程学院,辽宁 沈阳 110168)
1 引言
空间机械臂在执行在轨对接或装配任务时,通常有多种任务要求,以及降低冲击脉冲的要求。碰撞脉冲力的减小需要建立在碰撞动力学模型的基础上。在多体系统碰撞动力学建模领域,已有学者开始进行研究。虽然现有的机械臂轨迹规划方法非常丰富,但很难同时满足上述相关要求和影响性能指标。文献[1]提出一种基于人工势场法的冗余机械臂避障轨迹优化。建立冗余度机械臂的运动学模型,用高斯函数建立虚拟重力势场来处理局部极小问题。文献[2]提出一种基于蛇形曲线的流场中蛇形机器人避障轨迹优化。考虑流体环境对蛇形机器人系统的外部干扰,采用浸入式边界格子Boltzmann 方法建立障碍物通道与流固耦合模型,实现蛇形机器人的运动轨迹跟踪达到有效避障的目的。
但是上述两种方法在超冗余机械臂避障轨迹中耗时过长、稳定性也较差,不适用于精度要求较高的场合。提出一种考虑任务优先级的避障轨迹优化方法。考虑任务优先级实施合理排序,引入臂平面和避障面,运算出超冗余度机械臂的运动学逆解。最后利用任务优先级转换的避障算法对超冗余度机械臂的避障轨迹进行优化。
2 任务优先级确定
在机械臂执行在轨对接或装配任务时,通常会有多重任务要求。任务优先级用于区分不同任务约束的优先级,首先满足高优先级任务约束,然后依次处理低优先级任务约束,不影响高优先级任务约束。根据任务优先级,设定出2 个子任务r1∈Rm1和r2∈Rm2,其中子任务r1比子任务r2的优先级高,q∈Rn所描述的是关节空间变量。q 与ri两者之间的微分联系表达式即:

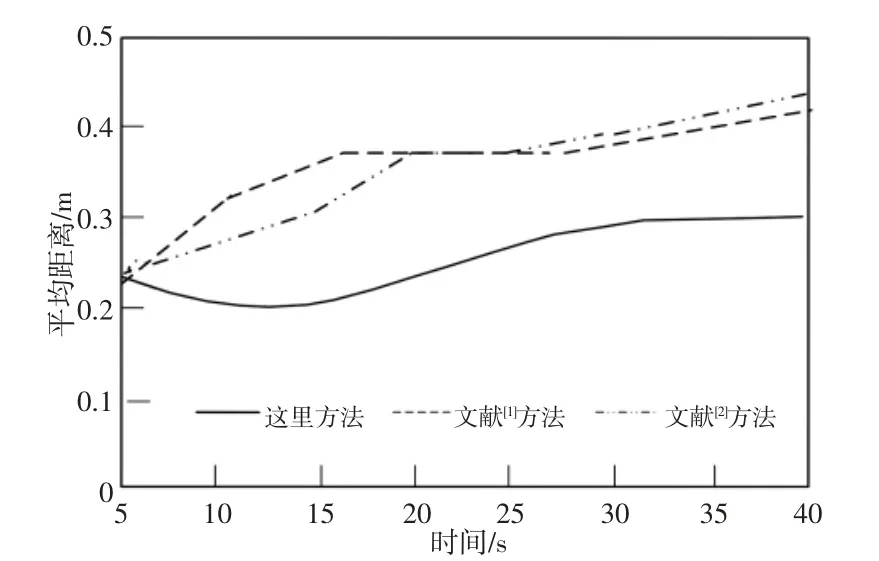
其中,Ji(q)=∂ri/∂q∈Rmi×n作为机械臂的雅克比矩阵。当mi 其中,右边第一项是式(1)的最小范数解,第二项是与式(1)对应的齐次线性方程的通解。代表雅克比矩阵J1的广义逆,I∈Rn×n代表单位矩阵,v 代表在n 维实空间Rn内的任意矢量,可称之为任意的关节速度矢量代表零空间投影矩阵,代表v 在零空间内(N)J 的投影。把式(2)代入到式(1)中,需要使式(1)内i=2,能够得出公式为: 根据式(3)能够获得矢量v 的解,公式为: 然后,将式(5)进行简化处理,得出公式为: 通过式(6)可知,在对下文处理的机械臂避障运动学逆解时[3],低优先级任务不会影响高优先级任务,确保低优先级任务的精度。 图1 7 自由度机械臂结构模型Fig.1 Structural Model of Manipulator with Degree of Freedom 7 自由度机械臂结构模型,如图1 所示。该模型7 个关节均为旋转关节,其中1 轴与电机减速器直接连接,2 轴和3 轴为平行轴,4 轴为左右摆动关节,5 轴、6 轴和7 轴为腕关节。这种结构不仅优化了腕部关节的运动性能,而且还大幅提高了机器人的工作空间范围和工作精度。 与传统的非冗余度机械臂比较而言,超冗余机械臂可以利用冗余度自由度巧妙地避开障碍物,符合机械臂末端位置达到预定任务空间的规格充分发挥超冗余机械臂的运动特性[4]。 在不影响最终任务性能的前提下,对目标函数进行优化。通过一种避障面,并将臂角定义为避障面与臂平面的夹角。若确定了臂角,那么避障面也随之确定[5]。使作为位置矢量,Rj∈R3×3作为旋转矩阵,j 作为参考点。根据手臂平面到避障面的预期自运动,可以作为旋转角度,旋转角度等于手臂角度。矢量的运算公式为: 其中,dse所描述的是上臂长度,dew所描述的是下臂长度,并且需要注意的是的表达式不是唯一确定的,会跟随机械臂参数的定义发生改变[6]。期望臂平面到避障面臂角的旋转矩阵的运算公式为: 式中:fmax—虚拟排斥力的最大数;K—比例系数,其表达式为: 式(13)的概念相当于机械臂的两层保护。在第一层保护内,当机器臂靠近障碍物移动且d 小于安全距离dsafe时,虚拟斥力fv值从0 持续变化到fmax。在第二层保护内,当机械臂离障碍物较近且d 小于极限距离dlim时,虚拟斥力fv 值始终为fmax。此阶段处于紧急状态。为了能够保护机械臂,需要暂时减慢或者停止末端执行器的动作,等待机械臂安全离开极限区域,然后恢复操作[8]。 当环境内有多个障碍物时,虚拟斥力fv 能够作为对应于多个障碍物的虚拟斥力之和,即: 其中,fvn所描述的是对于第n 个障碍物的虚拟排斥力。 针对上述情况,引入一个变换变量,根据机器臂与障碍物之间的距离来改变主从运动的优先级。在运动过程中保持良好的姿态,需要把避障运动的操作空间转化成一维空间。将避障运动的操作空间缩小到一维空间内。设定d0代表障碍物上临近点标志点的矢量,其公式为: 那么标志点运动的雅克比矩阵的简化公式为: 超冗余机器臂的运动学逆解为: 将其简化处理,得出公式为: 根据任务优先级转化的避障算法表达式为: 在上述公式中,v0所描述的是设定的标志点避障速度的初始值,α 和β 所描述的是代入的转化变量,其表达式为: 式中:‖d0‖—通过实时运算获得各构件与障碍物之间的最小距离;dm—给定的距离阈值。需要引入转化变量α 与β,需要引入转换变量,实现主从任务之间的优先级转换,以避免障碍物移动和机械臂运动结束。若最小距离‖d0‖的值较大,那么α=β≈0。式(19)将变为: 由此可见,机器人手臂的末端运动是机器人手臂的主要任务,几乎不受避障运动的影响,能够达到较高的末端跟踪精度。伴随机器臂接近障碍,在‖a0‖≈am的情况下,α=β≈1,式(19)将变为: 在此现象下,机器臂的避障运动是主要任务,但是,末端的轨迹跟踪误差会增加。若最小距离‖d0‖≈0,那么α≈2,β≈1。式(19)将转变为: 此时,避障运动仍然是主要任务,这将产生更大的避障速度。跟踪误差会增大。轨迹跟踪误差还会进一步增大,能够完成超冗余机械臂避障轨迹优化。 对一个7 自由度机械臂进行仿真研究。仿真实验操作系统为Windows2007,电脑内存为Intel R Core Tm i3-7100CPU3.90GHz,3.14GB,仿真软件为MATLAB2015a版。机械臂的轨迹优化任务要求机械臂的终点轨迹为直线段。在机械臂运动过程中,夹持器夹紧面与直线轨迹垂直,机械手工作空间存在空间障碍物。运动的过程是加速、匀速以及减速。比较避障轨迹优化方法与改进人工势场法的冗余机械臂避障算法(文献[1]),基于改进蛇形曲线的蛇形机器人在流场中避障的轨迹跟踪控制律(文献[2])方法的避障时间和障碍物与机械臂的最小距离。避障环境三维空间示意图,如图2 所示。避障空间使用两个(30×30×280)(单位:mm)的型材作为障碍物,两障碍物间距为0.16m,相对X 轴对称放置,布置在在实验室平整地面。目标物为(5×5×5)(单位:cm)正方体。规划机械臂需穿过两障碍物之间到达目标物,且不触碰障碍物,视为避障成功。 图2 避障环境三维空间及不同方法避障轨迹示意图Fig.2 Three Dimensional Space of Obstacle Avoidance Environment and Motion Trajectory of Different Methods 路径的初始构形[-136.85°,-74.35°,141°],初始位置为[-4182,-1573.1]mm,目标位置为[-3695,-4356]mm,做直线运动。在直线运动中主要观察关节臂前3 节的角度变化,对比期望值与实际值,两个值越贴近说明避障效果越好。具体实验结果,如图3 所示。由图3 可知,关节(1~3)的实际值曲线与期望值曲线存在细微的差别,是由于机械臂惯性导致的跟踪滞后,但基本重合,说明此次设计的方法完成避障效果达到了期望值。 图3 机械臂关节(1~3)的期望关节角与实际关节角对比Fig.3 Comparison between the Expected Joint Angle and the Actual Joint Angle of the Manipulator Joint(1~3) 机械臂成功绕开障碍物,并到达期望的末位置。机械臂与障碍的平均距离反应了避障过程中机械臂的稳定程度。平均距离的变化曲线,如图4 所示。通过图4 可以看出,对比方法的平均距离变化幅度在(0.22~0.41)m 之间,而机器人手臂与障碍物之间的平均距离维持在(0.2~0.3)m 之间,因此末端与障碍物之间不会发生碰撞,且稳定性较好。也就是说,当实现避障任务时,同时到达目标位置,证明了算法的有效。 图4 障碍物和机械臂的平均距离Fig.4 Average Distance Between Obstacle and Arm 针对以往冗余机械臂避障算法的不足,提出一种考虑任务优先级的超冗余机械臂避障轨迹优化方法。考虑任务优先级,进行有效排序建立结构模型,充分发挥机械手的运动特性。利用虚拟排斥力推导了超冗余度机械臂的零空间运动方程,利用逆动力学方法求出机械手与障碍物之间最小距离变化。利用任务优先级转换的避障算法对超冗余度机械臂的避障轨迹进行了优化。实验仿真结果表明:在避障过程中直线运动的关节角度实际值与期望值基本重合,且机械臂与障碍物平均距离在(0.2~0.3)m 之间。

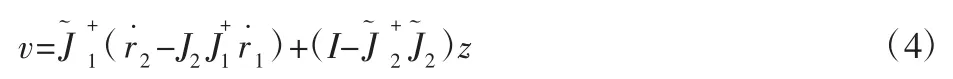


3 超冗余机械臂避障轨迹优化
3.1 7 自由度机械臂结构模型

3.2 避障问题的运动学逆解







3.3 避障运动操作空间缩减




3.4 避障轨迹优化





4 仿真实验与分析

4.1 直线运动实验

4.2 障碍物与机械臂的平均距离对比
5 结论

