基于ANSYS MW 级风电机组门洞焊缝的尺寸优化

李 健，孙 柳，焦 凯，江 涛

（1.常州大学机械工程学院，江苏 常州 213164；2.南京风电科技有限公司，江苏 南京 210046）

1 引言

优化设计的原理是将物理模型转化为数学模型，将限制条件转化为约束条件，然后运用最优化理论和方法，从全部可行方案中，选定最优设计方案。随着计算机技术的飞速发展，可将最优化理论与有限元法（FEM）结合应用于结构分析中，如此，任意复杂的问题都可以通过两种方法的结构响应进行研究。国内外主要在用于铰链梁的研究，并取得了一些成果[1-2]。

一般在保证门洞焊缝满足相应尺寸和强度的条件下，基于ANSYS 软件，结合二次拉格朗日非线性规划优化方法对MW 级风机的门洞焊缝进行尺寸优化。优化模型以门洞门框深度、门框厚度和门框长短径作为设计变量，焊缝Von-Mises 应力为目标函数，门洞大小不影响人员进出为侧面约束条件，对门洞进行尺寸优化，获得满足要求的结构尺寸，并以优化后的模型尺寸，重新建立门洞焊缝的分析模型，进行极限强度分析及疲劳寿命分析，达到减小应力、提高寿命的目的。

2 优化设计基本原理

2.1 结构优化三要素

优化设计是运用合理方法建立优化数学模型，并且用适合的优化算法进行迭代计算，以求得目标函数极值，从而得到最优设计方案。优化设计数学模型的三要素为设计变量、目标函数和约束条件。设计变量是优化过程中发生改变的一组参数；目标函数是随设计变量值改变而发生变化的值，可以是结构重量、结构体积等；约束条件是一个可行设计必须满足的某些限制条件，如强度、刚度等。

2.2 NLPQL 迭代算法

在ANSYS 软件中，选取的优化方法为二次拉格朗日非线性规划法（NLPQL），数学模型为：

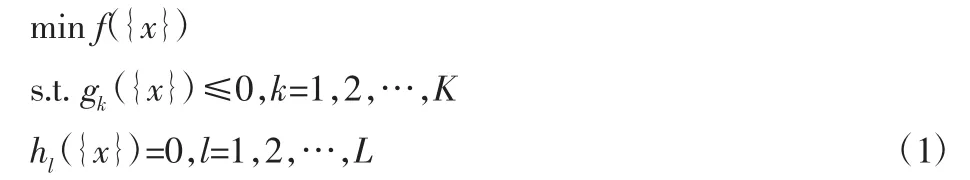
这里，K、L 分别是不等式约束和等式约束的个数。当x 有上下限时，即存在两个不等式约束。为了将优化目标近似成二次子问题，将不等约束条件假设为等式约束条件，则等式约束条件下的拉格朗日函数为：

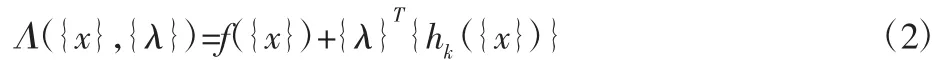
把式（2）作为一个新的无约束条件的目标函数来求解它的极值点，所得的结果就是在满足等式约束条件的原目标函数的极值点。根据极值的必要条件，可得l+n 个非线性方程，从而解得x=［x1，x2，…，xn］T和λ=［λ1，λ2，…，λl］T共l+n 个未知变量的值。所以式（2）可以改写为：

函数集｛F｝为：

参考牛顿法，式（3）中的向量｛Y｝，如下式更新：

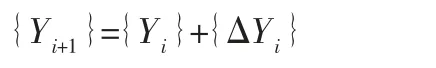
该向量的增量是由牛顿迭代公式（5）给出：

现考虑下面的二阶问题（6）：

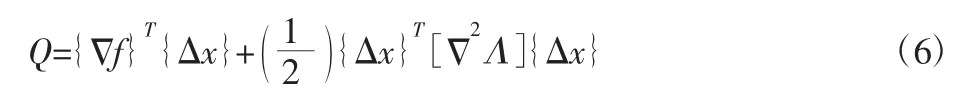
为了求出最小化问题，我们建立拉格朗日方程：

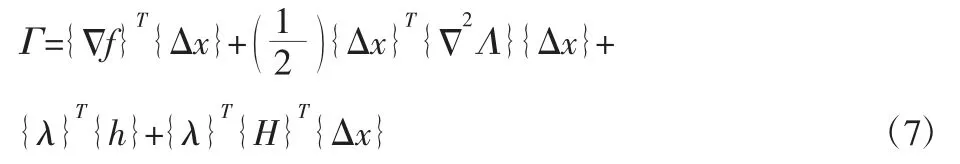
再考虑不等式约束，实际问题的拉格朗日也可以写成一下形式：

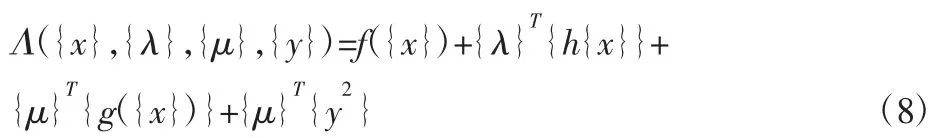
其中，不等式约束加入松弛变量转变为等式约束：

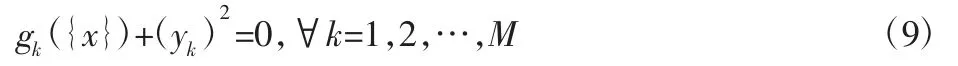
牛顿法应用的线性化方程组最终可以写为如下显示形式：

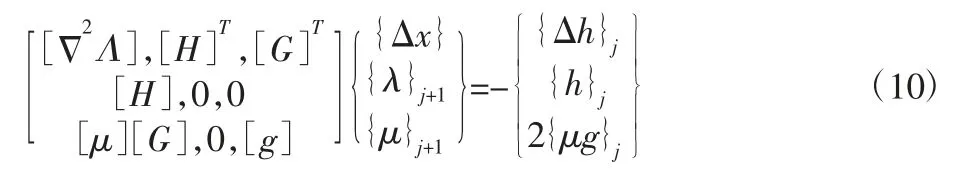
3 有限元优化模型的建立

3.1 有限元分析模型

门洞焊缝模型一般包含若干细小特征，如果在有限元建模中引入这些细小特征，会造成实际建模困难、网格数量偏多、网格质量偏差，从而增加计算时间和影响计算结果精度。因此在前处理过程中对这些细小特征进行简化，简化的原则是在保证计算精度的前提下，忽略对门洞焊缝关键部位应力影响较小的一些非关键细节特征，以提高网格质量和计算速度。

网格划分中，六面体单元除了在扭曲度方面比四面体低之外，其余方面综合性质均高于四面体。由于扭曲度对门洞焊缝的网格质量影响很小。因此，分析采用8 节点六面体单元对焊缝的几何模型进行网格划分。

3.2 定义设计变量、优化目标、约束条件

（1）设计变量。本次优化是在原有设计方案基础上进行的，与焊缝相互连接的其他部件均已确定。因此，本次的优化只选择门框深度、门框厚度、门框长径和门框短径为设计变量，门洞焊缝优化模型，如图1 所示。（2）目标函数。门洞焊缝在初始设计时，由于实际生产制造的限制，焊缝尺寸不够合理，虽具有满足设计规范所要求的强度，但安全余量较小。故本次优化以焊缝的Von-Mises 应力为目标函数。（3）约束条件。进行优化设计时，通过改变特征尺寸以达到降低应力的目的，应力的减小一般意味着尺寸的增加，优化过程中的将满足使用要求的尺寸作为约束条件。

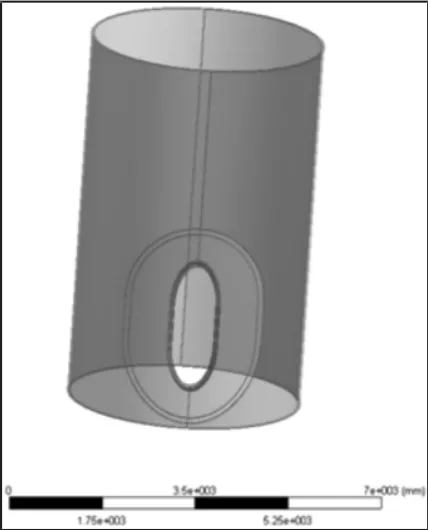
图1 门洞焊缝几何模型Fig.1 Geometric Model of the Door Weld

4 有限元分析的基本参数

4.1 门洞焊缝材料参数

设计中，塔筒材料选用Q345E，门洞焊缝选用E50 型焊条。分析过程中按照设置材料力学性能，如表1 所示。材料强度指标[3]，如表2、表3 所示。

表1 材料参数（常温）Tab.1 Material Parameter（Room Temperature）

表2 塔筒强度标准值Tab.2 Characteristic Value of Strength of the Material

表3 对接焊缝强度设计值（一级焊缝）Tab.3 Design Value of the Weld Strength（First-Grade Weld）

其中：根据DIN18800-1[4]，弹性模量E 的取2.1E+05 MPa。一级对接焊缝强度设计值根据GB50017[5]选取。

4.2 极限载荷及载荷加载方式

由风机整机动力学计算，确定出极限载荷，如表4 所示。载荷作用于塔底载荷坐标系[8]原点，塔底载荷坐标系，如图2 所示。

表4 极限载荷Tab.4 Ultimate Load

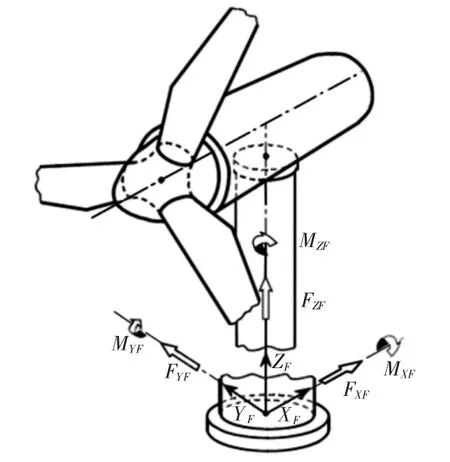
图2 塔底荷载坐标系Fig.2 Tower Coordinate System

5 门洞焊缝优化结果

优化前后的尺寸数据，如表5 所示。两者Von-Mises 应力分析结果[7]，如图3 和图4 所示。确定优化结果后，运用图5 中SN曲线，使用Miner 损伤累积法则[6]计算焊缝的疲劳损伤结果，如表6、图6 所示。结果对比表明，优化后的结构Von-Mises 应力和疲劳损伤均明显降低，达到了优化设计的目的。优化过程中，对目标函数Von-Mises 应力关于设计变量的依赖关系采用敏感性分析，分析结果，如图7、图8、表7 所示。

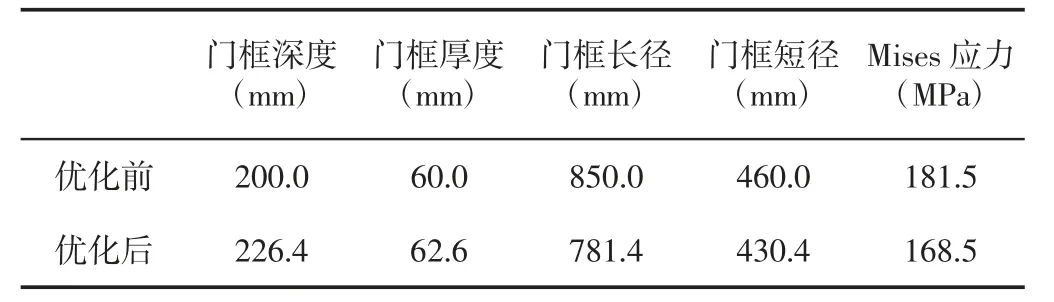
表5 优化前后模型比较Tab.5 Comparison Between The Original and Optimized Model

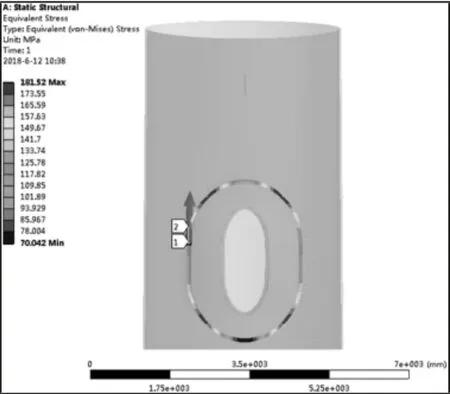
图3 优化前模型的Von-Mises 应力分布图Fig.3 Von-Mises Stress Contour of the Original Model

图4 优化后模型的Von-Mises 应力分布图Fig.4 Von-Mises Stress Contour of the Optimized Model

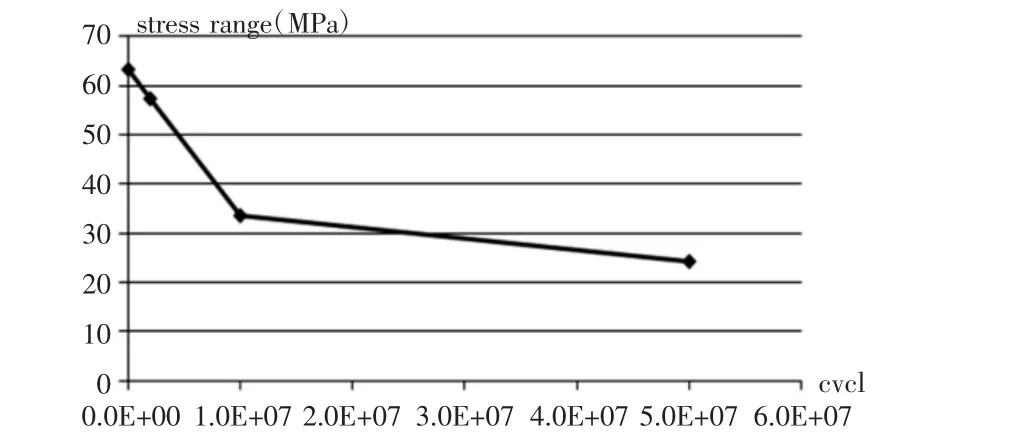
图5 门洞焊缝SN 曲线Fig.5 SN Curve of the Door Weld Joint

表6 优化前后焊缝的疲劳损伤对比Tab.6 Fatigue Damage of the Original and Optimized Model

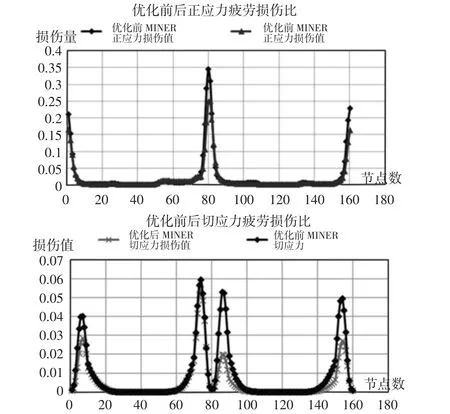
图6 优化前后疲劳损伤损伤对比图Fig.6 Fatigue Damage of the Original and Optimized Model

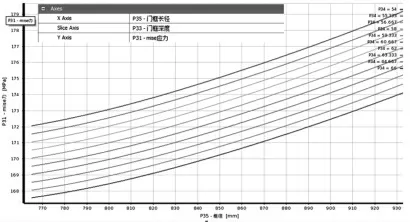
图7 极值点确认Fig.7 Confirmation of the Minimum Value

表7 Von-Mises 应力关于设计变量的敏感性系数Tab.7 The Sensitivity Coefficient of Von-Mises Stress vs.Design Variables

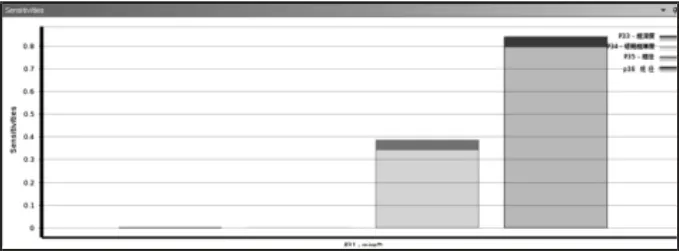
图8 Von-Mises 应力关于设计变量的敏感性系数Fig.8 Sensitivity Coefficient of Von-Mises Stress vs.Design Variables

6 结论

通过优化前后的模型计算对比，基于二次拉格朗日非线性规划优化方法和有限元方法的结构尺寸优化可以有效减小门洞焊缝的Von-Mises 应力，提高焊缝的强度安全余量；降低焊缝疲劳损伤，延长焊缝的服役寿命。敏感性分析表明，门洞焊缝Von-Mises 应力关于门框长、短径的敏感度远大于门框厚度及其宽度等参数，结论对于风电行业企业进行塔筒门洞焊缝设计提供了较大的借鉴意义。以ANSYS 等商业有限元分析软件为平台的结构优化方法对解决工程结构优化问题是实用的，可以有效缩短设计迭代周期，减少设计成本，是现代结构设计的一个重要发展方向。