吸盘机械手运动参数设计和优化
夏 梦,杨玉萍,季彬彬,陈丰明
(1.南通大学机械工程学院,江苏 南通 226019;2.无锡鼎茂机械制造有限公司,江苏 无锡 214107)
1 引言
近年来随着智能化、自动化技术的进一步升级,机器手被广泛应用于搬运、焊接、装配、喷涂及机械加工等诸多领域,其中搬运机械手用途最为广泛,主要用于自动化生产线的上下料、搬运及码垛等操作。然而,某些搬运机械手在特殊应用场合下,其执行末端需具有柔性特征,同时需要满足高速、高加速及频繁启停的生产工艺要求,这就使得机械手在完成预定动作后执行末端会产生残余振动,影响其定位精度和工艺质量[1]。
以吸盘机械手为研究对象,对其进行运动规划,该机械手是预装拉链工作台的子模块,其主要功能是将已裁切成形的塑料拉链搬运至目标位置进行压烫。吸盘机械手执行末端为硅橡胶吸盘,具有柔性特征,由生产工艺及效率要求确定其纵向搬运距离为162mm,定位精度为±0.02mm。预装拉链工作台的最大工作速度为120Pcs/min,吸盘机械手需在0.5s 内完成拉链吸取、纵向进给、热封延时、拉链脱开、纵向复位等一系列动作。由于机械手运动较为频繁,如果在运送过程中出现较大的冲击振动,必然会导致吸盘工作异常,造成拉链放置歪斜,甚至出现拉链脱落现象,严重影响拉链薄膜的生产质量,因此,对吸盘机械手的运动规划显得尤为重要。论文基于Adams 软件对吸盘机械手的速度进行梯形曲线和S 形曲线规划,结合仿真结果分析并优化了S 形曲线的运动参数,获得了冲击最小的运动曲线,保证了其运动精度和可靠性。
2 吸盘机械手几何建模
建立吸盘机械手的三维模型,如图1 所示。该结构以伺服电机为驱动系统,以同步带为传动系统,并由线性导轨、连接块、气动吸盘及吸盘固定架等构成执行系统。在导入Adams 分析前,为了减少计算量,有必要简化模型,简化后的模型只保留执行系统。
由于吸盘机械手的执行末端具有柔性特征,且对定位精度有较高的要求,为了精确的模拟出吸盘的运动状态,应用Adams软件建立刚柔耦合系统。柔性体在受力时会产生变形,而刚性体不受影响。连接块和线性导轨在运动中变形较小且对定精度影响较小,视为刚体,而吸盘变形较大,吸盘架需要分析应力应变,视为柔性体,如图1 所示。文献[2-4]建立柔性体有三种方法:离散柔性连接杆、FEA 有限元软件输出mnf 文件、ADAMS/ViewFlex 模块生成mnf 文件。第一种方法只限于构件是简单构件时使用,第二种方法需要定义外联点且柔性体替代刚性体时需进行位置调整,计算量较大。第三种方法直接将柔性体替换刚性体,替换后的刚性体的运动副或载荷等会自动转移到柔性体上,无需多余的操作就可以进行运动仿真,为使问题简化,采用第三种方法[5]。建立的刚柔耦合模型,如图2 所示。

图1 吸盘机械手三维模型Fig.1 3D Model of Sucker Manipulator

图2 吸盘机械手刚柔耦合模型Fig.2 Rigid Flexible Coupling Model of Sucker Manipulator
3 运动曲线参数设计与仿真
根据机械结构组成和工艺要求确定相关参数,吸盘机械手采用伺服电机的额定转速n 为3000r/min,同步带轮的齿数Z 为30,节距P 为5mm。吸盘架通过同步带固连,将电机的回转运动转化为平动,经计算机械手的额定速度为2000mm/s。机械手允许的最大加速度由伺服电机、传动装置和负载的运动状态决定,一般由现场调试确定。加速度越大,机械手工作时间越短,工作效率越高,而运动冲击引起的振动也越强烈,加速度过大不仅影响吸盘的定位精度还会降低相关零件的使用寿命,所以确定合理的最大的加速度至关重要。
3.1 梯形运动曲线设计
实际生产中常用的运动曲线为梯形曲线,梯形曲线为3 段方程曲线,相比S 形7 段方程曲线计算简单,实现容易[6]。设梯形曲线各段加速度数值均为ai,目标位移为162mm,加速时间为t1,匀速运动时间为t2。梯形曲线的加速度函数如下:

已知V=2000mm/s,S=162mm,可以求得t1+t2=0.081s。
通过上述条件可以参数化加速时间来驱动机械手的运动仿真。对机械手驱动类型为加速度,运动方向为Z 向。设计变量加速时间设为t1,标准值为40ms,取值区间为(20~60)ms。设计5 组实验,即对20ms,30ms,40ms,50ms,60ms 的加速时间进行分析。取图2 中的A 点作为执行末端的测量点,设定仿真时间为0.2s 和仿真步数为300 步。
Motion 函数如下:

机械手沿Z 方向(机器纵向)运动,如图2 所示。执行末端为柔性体,在Z 向运动平稳,变形不大,但在X 方向(机器横向)和Y方向(与地面垂直)出现了明显的变形,如图3、图4 所示。

图3 吸盘节点X 方向的形变曲线Fig.3 Deformation Curve of Sucker Node in X Direction
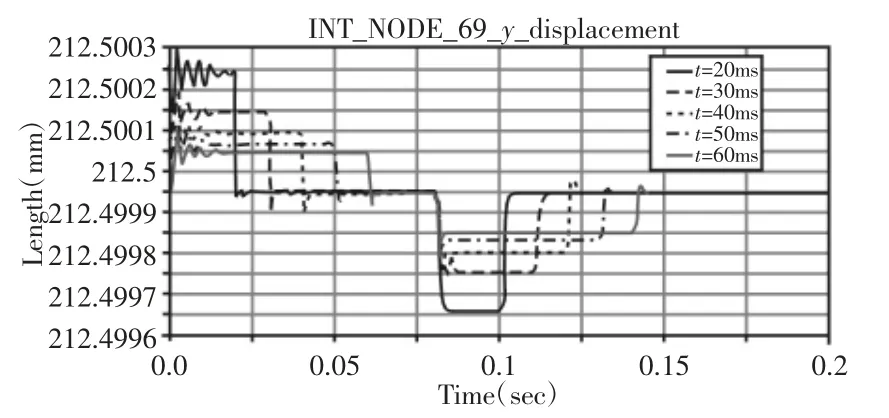
图4 吸盘节点Y 方向的形变曲线Fig.4 Deformation Curve of Sucker Node in Y Direction
从图3 图4 可以看出吸盘在X 和Y 方向变形的时间节点基本一致,但在X 方向振动更剧烈。启动初期吸盘形变较大,振动最剧烈,匀速运动时,形变稍小,减速时,形变又开始增大,到达目标位移后,该节点仍在振动,影响定位精度。X 和Y 方向振动幅度最小的是t=60ms 的曲线,振动结束时间最短的是t=20ms 的曲线,加速度越大,运动时间越短,但形变量越大,振动越剧烈。辅助设备的工艺要求机械手应在0.15s 内到达指定位移并停止振动,满足该要求的曲线是加速时间为20ms,30ms,40ms 的曲线,为保证运动过程的平稳性,选取加速时间为40ms,加速度为50000mm/s2梯形曲线作为机械手的最大工作速度时的运动曲线,其速度曲线如图4 中T-curve 所示。
3.2 S 形运动曲线设计与仿真
梯形曲线的加速度是突变的,容易对运动系统造成冲击,而S 形曲线的加速度是连续变化的,相比梯形曲线更具有优势[6-10]。为了增强机械手的运动平稳性,需进行S 形速度曲线规划。
设S 形曲线的阶跃为Jt,变加速的时间和匀加速的运动时间相等为t3,由于是在梯形曲线的基础上优化,匀速运动时间,总体运动时间,最大速度,位移,与T 形曲线一致。根据S 曲线阶跃、加速度、速度、位移之间的关系,可以求出Jt=5625000mm/s3,amax=7500mm/s2。
对S 形曲线进行仿真分析,motion type 为加速度,运动方向为Z 向,驱动函数为:

选取图2 的A 点作为执行末端的测量点,从图3 图4 可知,X 方向的振动更剧烈,所以仅测量该节点在XZ 方向的速度,并与梯形曲线对比,如图5、图6 所示。

图5 Z 方向的梯形速度曲线和S 形曲线Fig.5 Trapezoidal Velocity Curve and S Curve in Z Direction

图6 X 方向的梯形速度曲线和S 形曲线Fig.6 Trapezoidal Velocity Curve and S Curve in X Direction
由图5 可知,Z 向的S 形速度曲线相比梯形速度曲线更加平滑。图6 则表明,当机械手处于启动和变速状态时梯形曲线在X方向上会产生较大的波动,而S 形速度曲线只在启动阶段会有微小的抖动,这是由于梯形曲线在变速时,加速度是突变的,跃度趋向于无穷大造成的。
由图3 图4 可知,相同的线形,加速度越大,对运动零件造成的冲击越大。由于S 形曲线相比梯形曲线多了变加速的过程,相同的最大加速度,S 形曲线完成相同位移的时间更多,为了保证相同的运动时间,需要增大S 形曲线的最大加速度,因此需要对比两种曲线对零件的运动冲击。通过Adams 后处理模块的Animation 功能显示吸盘固定架的应力应变情况,吸盘固定架S曲线和梯形曲线的应力应变云图,如图7 所示。
S 形曲线和梯形曲线对吸盘安装架的的最大应力分别为0.334472MPa 和0.364754MPa。尽管S 形曲线的最大加速度大于梯形曲线,但是由于S 形曲线变速平缓,其造成的运动冲击仍然小于梯形曲线。

图7 S 形曲线和梯形曲线的应力应变云图Fig.7 Stress-Strain Nephogram of S Shape Curve and Trapezoidal Curve
4 S 形曲线参数优化
4.1 优化模型
由本分析可知,S 形曲线运动平稳性明显优于梯形曲线,但由于惯性的影响,其在加减速状态下运动仍然存在柔性冲击。吸盘机械手的执行末端是硅橡胶,属于超弹性体,运动过程的振动明显要高于刚性零件,尤其是在启动阶段。S 形曲线一般选取对称的形式,每个变速阶段的阶跃大小相等,但是这并非最好的运动规划参数,因为这样的曲线没有将惯性能在时域上进行最优分配,而非对称S 曲线运动中的不同运动段选用合适的运动参数可以抑制运动过程中产生的振动,能更合理地分配惯性能[1]。
通过Adams 的参数优化模块对S 形曲线的跃度进行优化,以获得波动最小的运动曲线参数。由于执行末端只在启动阶段产生较大的振动,且停止阶段的振动较小,所以对加加速和减加速阶段的阶跃进行优化。在仿真模型中,设加加速和减加速的阶跃为J1、J2,运动时间为T1、T2,匀加速时的运动时间为T3,目标位移为Q,Z 方向的最大运动速度为Vmax。根据S 曲线跃度、加速度、速度、位移之间的关系,建立约束:J1*T1=J2*T2,T1+T2+T3=0.04s。为了使运动过程中的振动最小,优化目标是执行末端在X 方向速度的最大值,设为Max(Vx),优化变量为J1、J2、T1、T2、T3。优化模型如下:

4.2 优化过程和结果
设J1、J2的初始值均为1.0×107mm/s3,T1、T2、T3为0.01s,设置仿真步数为200,仿真时间为0.2s,采用OPTDES-SQP(序列二次规划法)进行优化,各运动参数优化结果,如表1 所示。

表1 各运动参数优化结果Tab.1 Optimization Results of Motion Parameters
迭代优化过程,如图8 所示。由图8 可得,经过6 次迭代优化后,Vmax基本趋于稳定,第7 次达到最小值,Vmax从0.323187 下降到0.0576516,减少了82.2%。对比上述S 曲线0.1451mm/s 的最大速度,优化了60.26%。优化后加加速和减加速阶段的跃度为4.62×106mm/s3、6.73×106mm/s3,加加速、匀加速、减加速的运动时间为0.017774s、0.010020s、0.012207s。最优S 曲线降低了启动时的跃度,延长了启动加加速阶段的时间,虽然增大最大加速度,但是合理分配了运动各个阶段的时域惯性能,使得运动曲线更加平缓。执行末端X 方向速度的优化过程,如图9 所示。

图8 迭代优化过程Fig.8 Iterative Optimization Process

图9 X 方向速度曲线的优化过程Fig.9 Optimization of Velocity Curve in X Direction
5 结论
通过Adams 运动仿真软件,首先,对吸盘机械手的速度进行了梯形曲线规划,设置了5 组试验,得出:加速度越大,运动冲击越大,并根据设计要求的最大工作速度和定位精度要求,选择了合适的最大加速度。然后,在满足相同时间和位移的情况下,对机械手进行了S 形曲线规划,S 形曲线相比梯形曲线更平缓,在运动过程中X 方向和Y 方向产生的振动更小,尽管增加了最大加速度,吸盘固定架的应力应变云图显示S 形曲线的最大冲击应力依然小于梯形曲线。最后,基于Adams 参数优化模块对S 形曲线的加加速和加减速阶段的阶跃和各运动时间进行了优化,优化后的曲线减小了启动阶段的阶跃,延长了加加速的时间,使得启动时运动更加平缓。现场调试表明,这里提出的优化改进方法有效改善了吸盘机械手的运动精度和可靠性,实现了高速、高精度及高稳定性的工艺要求。

