爬楼轮椅运行复合参数多目标优化研究

曹永跃，魏永辉

（1.河南大学濮阳工学院，河南 濮阳 457000；2.燕山大学里仁学院，河北 秦皇岛 066004）

1 引言

轮椅使用者的活动范围随着无障碍设施的增加而变大，但是轮椅在楼梯间活动依旧受到一定的限制[1-2]。在智能轮椅开发功能中的导航功能存在运行偏移的情况，导致在爬楼的过程中，智能轮椅无法严格的按照规划生成路线，需要对轮椅运行过程中的路线以及姿态参数进行优化，以保证智能轮椅运动爬楼路线的准确性。

任猛基于利用步进电动机反向追踪车轮的纵向加速度以衰减轮椅座椅处纵向加速度的变化速度的原理，使用加速度传感器探测轮椅行驶状况，将信息传递到控制系统，控制动力源做出实时响应。根据路面激励对轮椅姿态进行调节，显著提高了轮椅行驶时的平顺性[3]。但现阶段使用的参数优化方法普遍存在两个较为严重的问题，一个是姿态调节方法无法适配于智能轮椅上，而另一个问题就是当智能轮椅处于信号复杂的运动环境中，姿态调节的容错性大大下降，即抗干扰性较低[4-5]。

针对上述问题，需对其进行多目标优化，引入NSGA-Ⅱ算法，将这种技术应用到爬楼轮椅运行参数优化当中，可以计算出规划爬楼路线与实际路线的偏移情况，以此为数据基础实现姿态的调节。通过对传统调节方法的优化设计，在保证调节功能正常运行的同时，优化轮椅运行参数，提高了姿态调节的工作性能。

2 爬楼轮椅传感器与控制器改进设计

智能轮椅姿态参数调节涉及到传感器与控制器的规划，主要用来采集初始信息，为姿态参数调节提供数据来源，生成对应的调节任务程序[6-8]。为了解决传统方法中存在的适配性的问题，需要改装传感器与控制器设备。

2.1 传感器与控制器的选择与应用

2.1.1 横摆角速度传感器

改装传统的角速度传感器，由于智能轮椅在一般情况下只在平面上运动，不涉及到空间竖直方向上的位移，因此在传统传感器的基础上加入横摆方向[9]。

2.1.2 姿态参数传感器

智能轮椅中应用的姿态参数传感器包括一个倾角传感器和一个陀螺仪，由此构成姿态参数传感器用来监测智能轮椅平台的运行姿态参数[10]，如表1 所示。

表1 传感器改装结果Tab.1 Modification Results of Sensors

2.2 姿态参数调节控制器

调节控制器的控制核心为TM320LF2407A 芯片，根据软件程序生成调节任务指令，通过一定的调节策略计算出偏移量和调节值[11]，再经过脉宽调制调节控制以及驱动设备放大处理，驱动直流电动机运转，及时调整智能轮椅的运动角度和运行速度，从而实现对智能轮椅姿态参数的调节。

3 爬楼路线与姿态复合参数多目标优化

在上述传感器与控制器调试完成的情况下，实现调节功能。智能轮椅依照生成的爬楼路线移动到指定的位置[12]。

3.1 NSGA-Ⅱ算法流程

对复合参数进行多目标优化，通过非支配排序NSGA-Ⅱ算法，降低了计算复杂度，将父带种群与子代种群进行合并，在双倍空间中选择下一代种群，使得种群中优秀个体得到保留。

（1）采用实数编码：根据实数编码方式，1 个实数对应1 个等位基因；

（2）初始值赋给：给定各个设计变量初始值，使其处于0 到1之间，随后通过随机函数产生初始值；

（3）适应度函数：在种群非支配函数过程中，给定不同非支配层虚拟适应度值，加快算法收敛速度，使非支配层收敛于最优区域；

（4）遗传算子：通过轮赛制的方式对算子进行选择，选择两个个体，选择非支配排序序号较小的个体，若比较过程中发生排序序号相同，则根据拥挤距离进行个体选择，选取拥挤距离较大的个体，采用二进制交叉算子，选择多项式变异算子作为编译算子；

（5）运行参数：种群大小选择为500，变异概率为0.1，交叉概率为0.9，运行迭代数为500。

多目标优化测试函数ZDT1、ZDT2、ZDT3 分别如下所示：

引入变量，构建等价关系，根据重要性的不同对各个目标fi（X）赋予一定的权值，将其映射到偏好点附近的权值向量修改为ωi=（fi1，…，fiM），其中：

在权值赋予过程中，动态惯性权值呈现线性变化，其大小会随着测度函数改变出现变化，对此，可以通过线性递减权值对惯性权值进行动态计算，即：

式中：Tmax—最大迭代数；ωmax、ωmin—最大惯性权值和最小惯性权值。确定各个单目标优化的权值，依据转弯角约束以及爬行仰角约束，获取多目标最优点。

3.1.1 转弯角约束

智能轮椅的速度与转弯角之间具有密切关联，最大转弯角要满足物理约束的限制，爬行路径的转弯角应小于或等于预先设定的最大角度。转弯角约束函数可以被定义为：

式中：p—常数，在爬行路线中有转弯角大于预设的最大转弯角时应对该路线加以约束，不利于爬行的路线可以通过增加P值与可行路线进行区分；αmax—设定的最大转弯角；αi—水平爬行路线上路径点i-1、i 和i+1 组成的转弯角。

3.1.2 爬行仰角约束

爬升仰角代表垂直方向的角度变化，在智能轮椅在爬楼过程中出现改变高度的动作时需加以考虑。最大坡度角限制了垂直方向的轨迹，爬升仰角的约束函数可以被描述为：

式中：［βmin，βmax］—爬行仰角的范围；βi—第i 个倾斜角，由i-1、i 间的路径点组成。

多个目标综合优化的最优点表达式如下所示：

综上得到多个目标综合优化的最优点，实现遵循最短路径原则和避障原则多目标优化。

3.2 智能轮椅移动爬楼路线规划优化

假设智能轮椅的初始位置坐标和目标位置坐标分别为（x0，y0）和（xn，yn），设置移动的初始速度为v，加速度为a[13-15]。将规划环境中的任意一个障碍点O 的坐标用（xO，yO）表示，那么该障碍点产生的势场可以表示为：

式中：r—以障碍物为中心的干扰半径。当式（2）中的计算结果<1时立即调整移动方向，最终所有移动路径点组成的移动路线可以用式（11）来表示。

为了保证位置定位结果的准确性，标定并配准定位坐标。当智能轮椅的位置与目标位置的坐标重合时，路线规划结束，得出由若干个平面节点组成的移动路线。

3.3 多目标优化特征匹配

多目标优化技术的实现建立在对应的硬件设备的基础上，遵循最短路径原则和避障原则，搜索到实际移动路线与规划移动路线之间的偏移节点，并计算出偏移量。假设在（xi，yi）位置上出现路线偏移情况，则该点为偏移节点，偏移量可以用式（10）来计算。

接着计算该点的位姿情况，计算公式可以表示为：

式中：S—当前位姿的泰勒系数；Tk—传感器采集的第k 个位置信息[16]。

以计算得出的偏移节点和偏移量为数据基础，分别从智能轮椅的角度、位置和速度三个方面调节轮椅姿态参数[17]。通过对应的硬件设备得出有关于姿态参数的偏移量解算结果，记为β。那么调节的过程即可以用式（12）来表示。

式中：q（n-1）—移动路线中上一个特征节点的位姿值；qt—实际运行中当前节点的位姿值。将智能轮椅恢复到上一个步骤并按照调节结果重新移动，从而实现智能轮椅位姿的调节[18]。

4 测试实验

为验证NSGA-Ⅱ算法的爬楼轮椅运行参数多目标优化研究设计成果的性能，设计测试实验。为了保证测试实验结果的变量唯一，需要保证测试环境与实验对象均相同。按照智能轮椅姿态调节方法的设计过程，改装并调试实验对象。可以实际移动路线特征点的提取结果，如图1 所示。

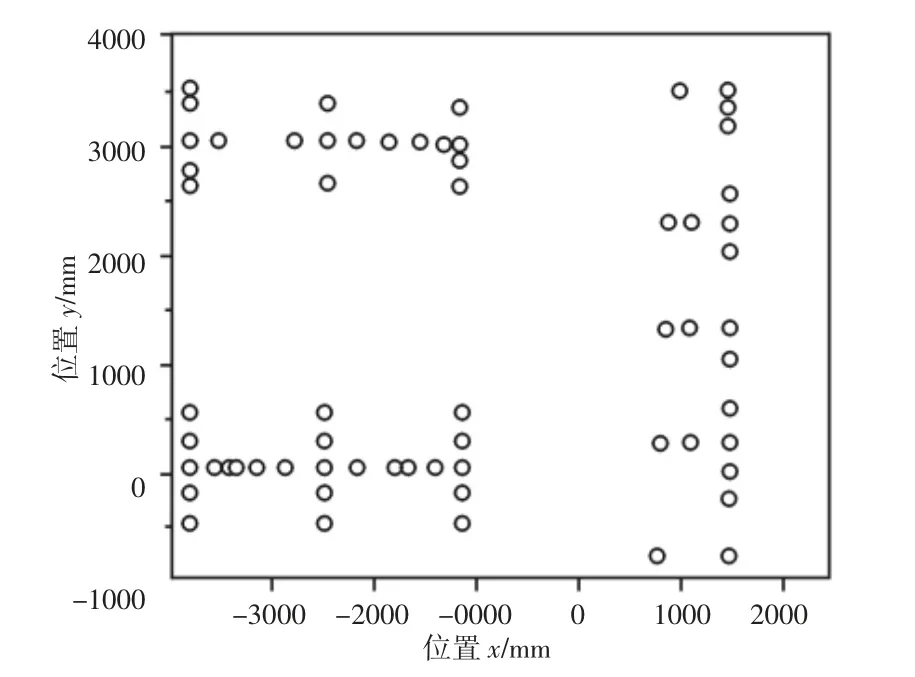
图1 爬楼路线特征点提取结果示意图Fig.1 Schematic Diagram of the Result of Feature Point Extraction of the Route

主要就是检测通过优化设计是否解决了传统方法中存在的适配的问题。得出功能测试的实验结果，如表2 所示。

表2 功能测试结果Tab.2 Functional Test Results

通过调节，测量值无限靠近设置的标准值，将表中的数据输入到Develve 统计软件中，经过统计、分析与对比发现基于NSGA-Ⅱ算法的智能轮椅姿态调节匹配程度为92%，而传统方法仅为85%。

为验证基于NSGA-Ⅱ算法的多目标优化性能，采用ZDT1、ZDT2、ZDT3 多目标测试函数进行实验。假设ZDT1、ZDT2、ZDT3三个测试函数所对应的种群个数均为100，最大迭代次数分别为100、200、400。在线性递减惯性权值中，ωmax=0.7、ωmin=0.4，线性递减惯性权值实验运行30 次。多目标优化测试函数ZDT1、ZDT2、ZDT3 的计算时间，如表3 所示。

表3 多目标测试函数计算时间Tab.3 Calculation Time of Multi-Objective Test Function

由表3 的时间结果可以看出，相比于ZDT2、ZDT3 函数的计算结果，ZDT1 函数所对应的计算时间较短，证明收敛速度较快，表明这里方法多目标优化速度较快，具有较好的优化效果。

通过求解得出路线特征的多目标优化结果，如图2 所示。

图2 多目标特征匹配示意图Fig.2 Mapping of Laser Scanning Features

由上图可以看出，多目标匹配后，爬楼轮椅路线得到纠正，能够准确沿着预期轨道行进。主要原因在于这里方法对运行中的路线设定以及姿态参数进行优化，引入了NSGA-Ⅱ算法，将这种技术应用到轮椅爬楼路线与姿态调节当中，可以计算出规划爬楼路线与实际路线的偏移情况，以此为优化数据纠正智能轮椅偏移路线。

5 结论

在爬楼的过程中，智能轮椅无法严格的按照规划生成路线，提出NSGA-Ⅱ算法的爬楼轮椅运行复合参数多目标优化方法，遵循最短路径原则和避障原则实施多目标优化，计算爬楼路线的偏移量，分别从运动角度、位置和速度三个参数实现对轮椅姿态的调节，实现复合参数多目标优化，能够在智能轮椅移动的过程中自行判别并调节轮椅路线与姿态。