提梁机车轮纯滑动时车轮和轨道的热弹塑性分析

乐 锋

（中铁十七局集团，河北 石家庄 050000）

1 引言

随着我国高速铁路的建设的发展，对大吨位提梁机的需求越来越多。提梁机属于典型的低速重载工程机械，目前对提梁机的研究内容很多，大多集中在强度和刚度等方面[1-3]，而对于某些细节方面却没有重视，如起重小车在运送梁的时候，有时候可能会出现车轮打滑的情况，尤其是制动时，此刻的牵引力和制动力大于粘滑力[4]，起重小车和轨道会发生滑动现象，滑动过程中的接触区会产生大量热量，致使温度升高，会对轨道和车轮产生不可修复的破坏，更严重的会对提梁机的安全产生影响。将运用有限元软件ABAQUS 建立提梁机的起重小车和轨道的热力耦合二维热弹塑性有限元模型，分析车轮和轨道在纯滑动过程中的温度场及应力场分布，以及残余应力及塑性应变变化情况，最后分析不同工作参数（工作载荷、摩擦系数、滑动速度）对结果的影响。

图1 某型号国产提梁机Fig1 Beam-Carried Crane

2 数值计算模型

2.1 轮轨接触模型

提梁机的车轮和轨道之间的接触关系可以简化为2 个圆柱之间的接触关系，如图2 所示。根据目前的文献[4-6]介绍，车轮和轨道之间的接触是满足Hertz 接触条件的。则两个圆柱接触区为椭圆形，如图3 所示。其压力分布可以由由Hertz 接触理论[5]得到：

式中：x1、x2—纵向和横向坐标；a、b—椭圆斑的长半轴和短半轴；p0—接触斑上的最大接触压力。其中：

式中：常数A 和B 具体数值可以参见文献[6]；系数m 和n 与A、B有关，亦可以由文献[6]查得。E1和E2代表车轮和轨道的弹性模量，v1和v2代表车轮和轨道的泊松比。

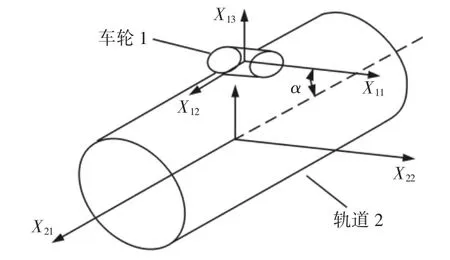
图2 车轮和轨道Hertz 计算模型Fig.2 Hertz Model of Wheel and Rail

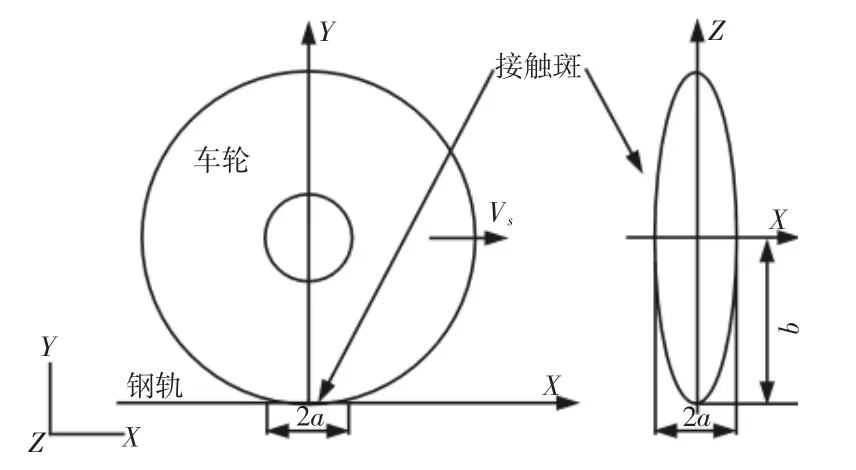
图3 接触斑示意图Fig.3 Schematic of Contact Spot

最大接触压力：

式中：W—轮重。

接触斑的切向力为：

式中：vs—车轮滑动速度。

故椭圆斑的热流密度为：

2.2 热力耦合模型

根据传热学理论，整个系统的温度场方程[7]方程如下：

式中：a—热扩散率；T—温度；t—时间。整个系统有三类边界条件：

（1）滚动前系统初始温度场：

（2）滚动时，系统产生的热流：

（3）滚动过程中的系统换热：

式中：λ—热导率；

Tw—界面温度；

Tf—环境温度；

h—表面传热系数；

n—边界法向单位向量。

2.3 有限元仿真模型

由于提梁机轮轨实际模型很复杂，所以需要建立简化的轮轨三维模型，如图4（a）所示。其次考虑到计算量，以及最大温度和应力分布在其截面中心，故最终二维模型作为分析对象，且在研究过程中发现温度及应力分布主要在接触区，故选择车轮的1/18 模型及取轨道的上轨面部分作为分析对象，如图4（b）所示。

直接在ABAQUS 软件中建立车轮和轨道二维模型，设置3个分析步，都选择Dynamic，Temp-disp，Explicit 分析步类型，第一个分析步加载机械载荷，时长0.1s，第二个分析步加载热流，时长4s，第三个分析步设置为冷却工况，将时长设置为10s。将轨道最底部全约束，车轮耦合到其旋转轴中心点，释放垂向和沿着轨道方向的自由度，并设置其匀速位移速度为0.1m/s，建立轨道和车轮直接的接触关系，设置摩擦系数为0.1。初始温度设置为20℃。使用CPE4RT 单元划分单元格。

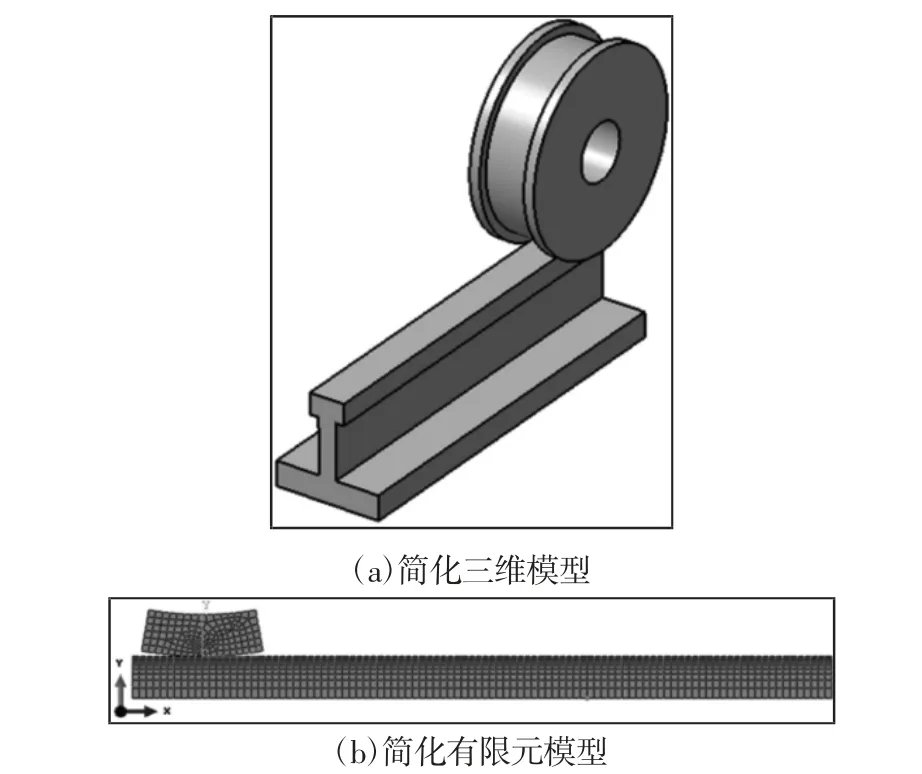
图4 简化三维模型及简化有限元模型Fig.4 Simplified 3D and FEA Model

材料部分，相关参数[8-10]，如表1、表2 所示。

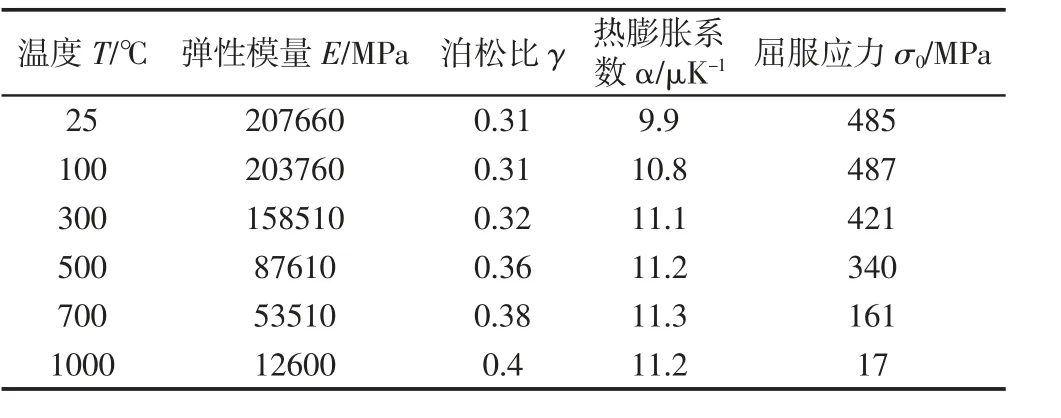
表1 弹性模量和泊松比Tab.1 Elastic Modulus and Poisson′s Ratio of Rock

表2 热传导系数和比热Tab.2 T Hermal Conductivity and Specific Heat

3 仿真结果与研究

3.1 温度场及应力场分布

本部分的分析工况为工作载荷500t、滑动速度0.1m/s、摩擦系数0.1。在只考虑机械载荷时，其应力分布，如图5（a）所示。由图可以看出，在机械载荷作用下，车轮和轨道的应力场分布形状呈现扇形，车轮和轨道的应力比较小，最大为262MPa，且最大应力点位置在车轮上；当车轮在轨道上出现纯滑动时，即机械载荷和热应力载荷的耦合工况时，其结果，如图5（b）所示。由图可以看出，耦合工况下的应力为632MPa，比纯机械工况提高近1.5倍。车轮上的最大应力分布主要在接触区域，而轨道上的应力分布呈现细长条状，其主要原因为热量的散失比较慢，车轮滑过后，没有散失的热量依然会影响轨道，其次是表层的热量渗透到轨道内部，在表面和内部的热量共同影响下，轨道的应力分布呈现细长条状。车轮和轨道的温度场分布图，如图6 所示。由图可以知道，最高温度已经达到了1126℃，最高温度点在车轮上，并呈现辐射状向车轮中心处分布，轨道的温度分布形状亦是呈现细长条状，其原因与轨道应力分布形状的一样。且由图可以明显看出，轨道的最高温度点相对于车轮的接触点，有明显滞后。

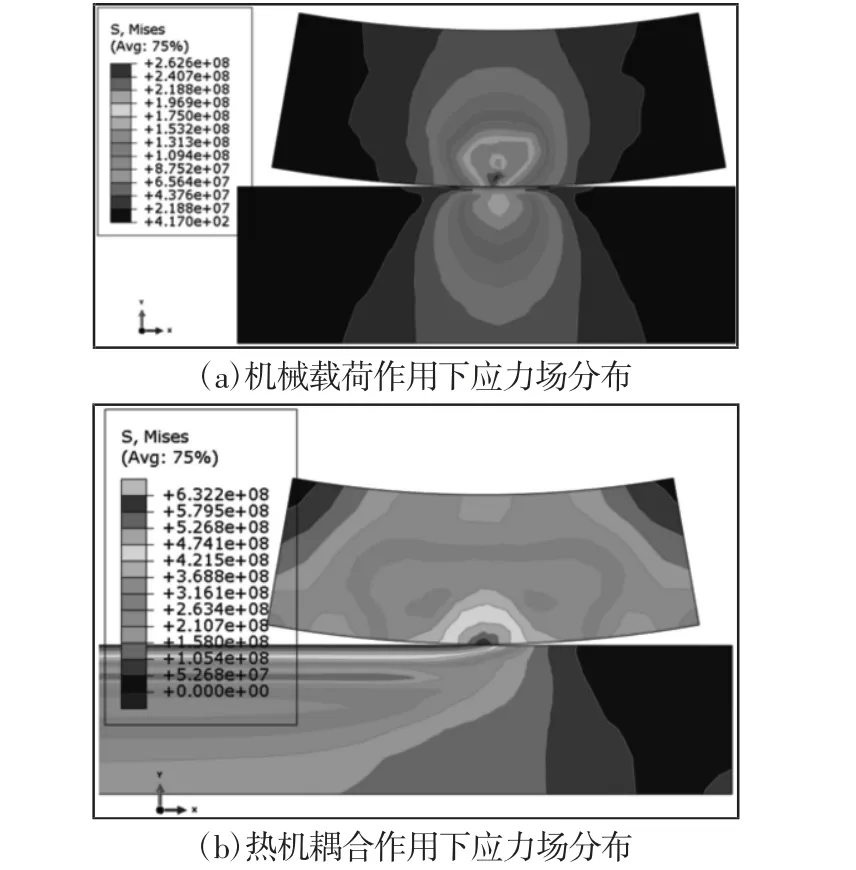
图5 应力场分布图Fig.5 Stress Distribution

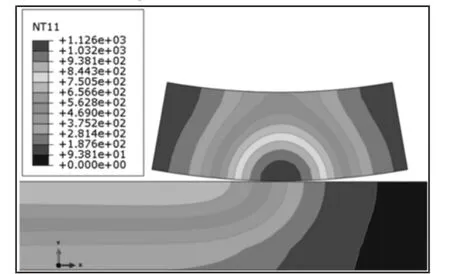
图6 温度场分布Fig.6 Temperature Distribution

分析车轮和轨道不同深度点的温度随时间的变化情况，具体，如图7 所示。由图可以，车轮表面温度最高，在滑动过程中，温度迅速上升，随着时间的增加，温度继续上升，但是上升幅度越来越小。其主要原因为在滑动过程中，车轮接触斑一直与轨道接触，温度会越来越高，但是随着与外界热交换越来越多，最终会达到平衡，所以温度上升速度越来越慢，最终会达到一个定值。应力的变化趋势与温度相似，在此不再说明。轨道表面的温度在接触斑到来后，迅速达到最高温，然后才缓慢降温，不同深度的温度变化略有不同，其原因为热量的传导需要时间。

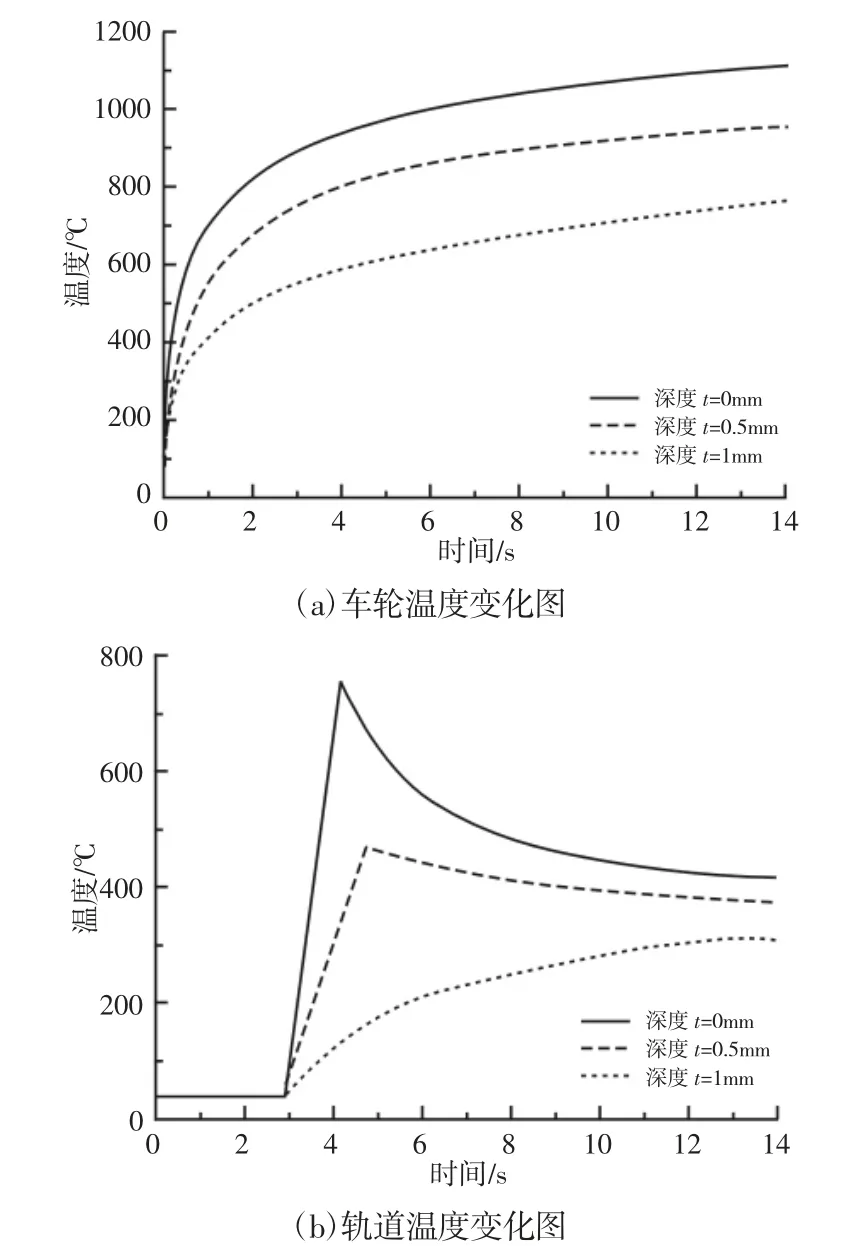
图7 车轮和轨道不同深度点温度变化图Fig.7 Change Chart of Temperature

3.2 塑性变形分析

由以上分析内容，高温导致的应力已经超过了材料的屈服强度，车轮和轨道都会发生塑性应变，此次只分析轨道的残余应力和塑性应变。残余应力为卸载后，温度回到常温时的应力大小，由于回到常温的运算时间非常长，此处的残余应力可等效为应力不变的情况，塑性应变亦是如此。为了消除边界效应，分析结果取轨道中间部分数据。具体结果，如图8 所示。

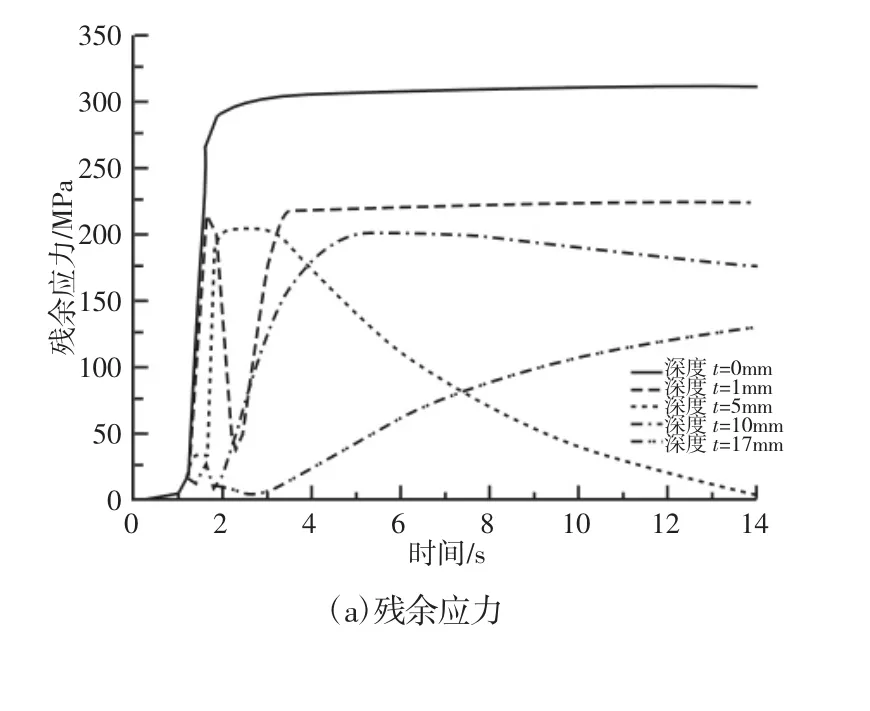
图8 轨道残余应力与塑性应变图Fig8 Residual Stress and Equivalent Plastic Strain of Rail

图8 （a）中可以看到轨道表层的应力在接触斑到来后，应力迅速升高，并且维持300MPa 左右不变，深度1mm 的变化趋势与表层相似，深度5mm 时，其应力迅速上升，后面再缓慢下降，深度越深，残余应力逐渐减小，并在一定深度点没有残余应力，此可以有图8（b）看出，图中深度0mm、1mm 和5mm 的塑性应变变化趋势与残余应力的变化趋势吻合，当深度为10mm 时，已经没有塑性应变发生。

3.3 不同工况研究

本节分析不同参数（工作载荷、摩擦系数和滑动速度）对结果的影响。将工作载荷P 分别设置为400t、500t 和600t，将摩擦系数μ 分别设置为0.1、0.2、0.3，将滑动速度v 分别设置为0.1m/s、0.2 m/s 和0.3 m/s。最终的结果，如图9 所示。由图可以得到，轨道的最高温度和最大应力值与工作载荷、摩擦系数及滑动速度基本呈现正相关关系，其原因可以有式（5）和式（7）看出，此三个参数与热流密度都是正相关关系。车轮的结果和轨道类似，在此不再赘述。

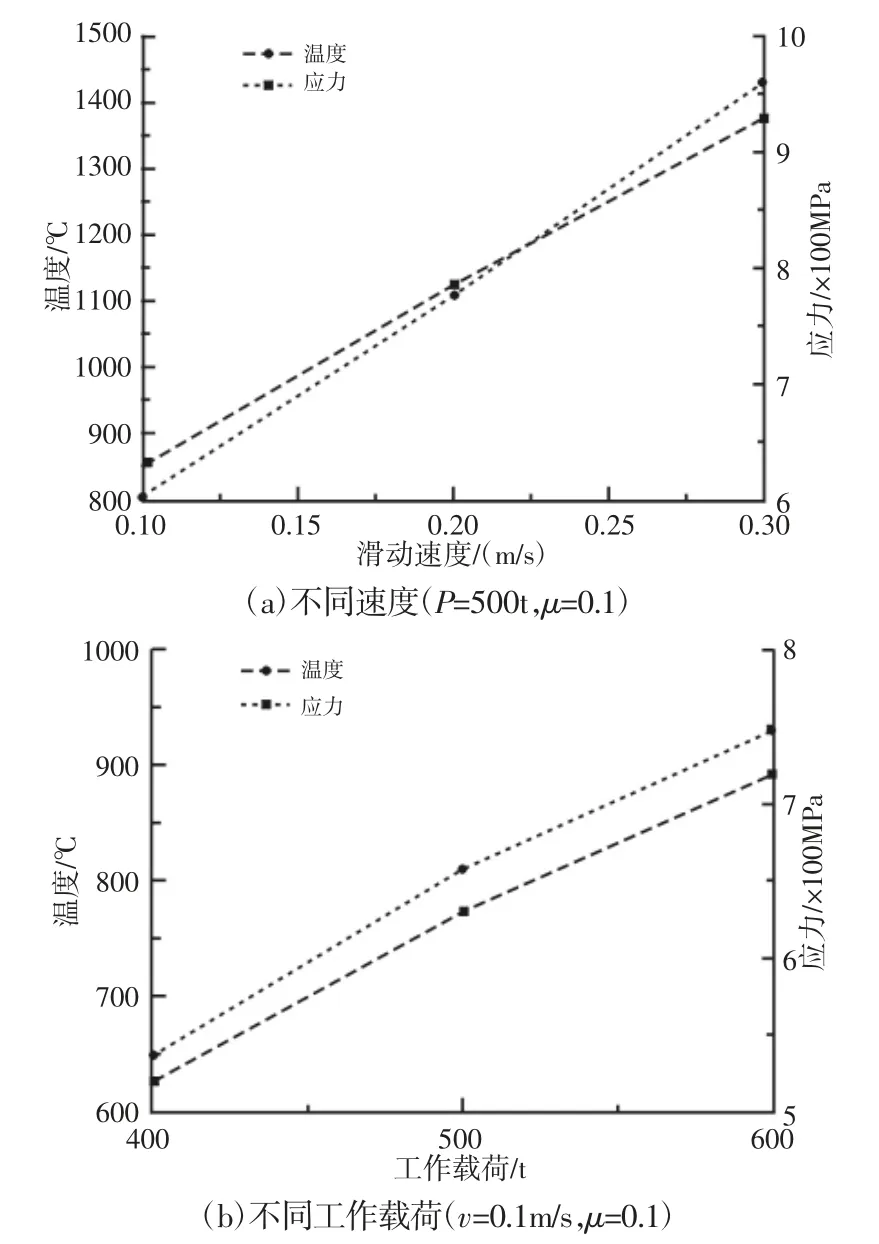
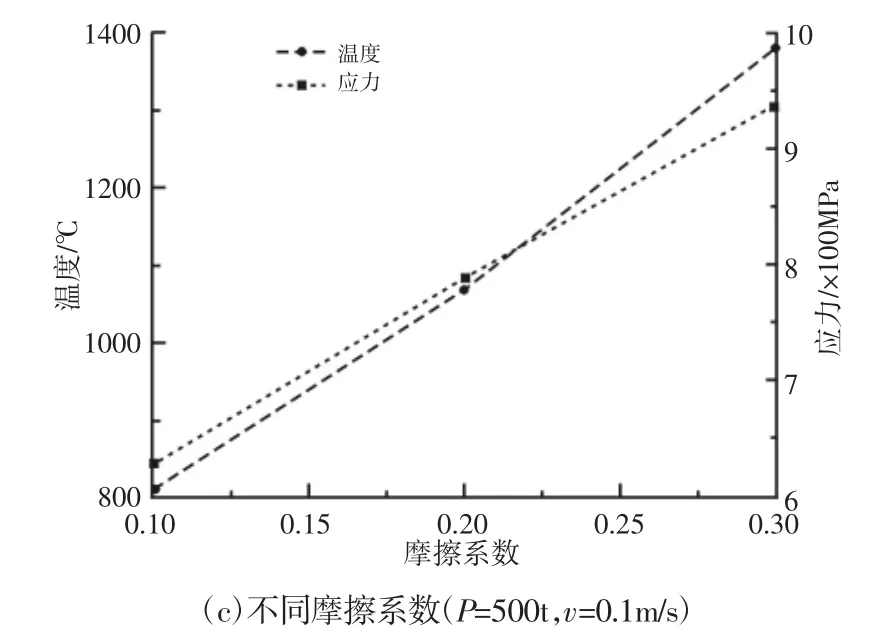
图9 不同参数对最大温度及应力的影响Fig.9 Temperature and Stress Influenced by Different Parameter

4 结论

（1）在纯滑动时，提梁机的最高温度在车轮的接触区上，而轨道上的温度低于车轮上，形状呈现为条带状；

（2）车轮上的温度呈现一直增加的趋势，但是温升量越来越小，轨道上的温度趋势呈现快速升高，缓慢下降的趋势；

（3）车轮在滑动过程中，会发生塑性变形，并会有残余应力产生；

（4）轨道的最高温度和最大应力和工作参数（工作载荷、摩擦系数和滑动速度）呈现正相关关系；

（5）要防止提梁机的车轮在运行过程中出现纯滑动现象。