车辆自载重测量系统的研究

何 磊，王志刚，郭宇飞，孟 浩

（武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉 430081）

1 引言

近几十近年来，我国道路运输车辆超载现象日益严重，因超载运输产生的道路维修费用高达几百亿元。为了消除超载现象，设计一种车辆称重装置显得尤为重要。现代学者们提出了几种载重测量方式，如：车辆电容测量装置[1]、BP 神经网络车辆测量装置[2]、位移传感器车辆测量装置[3]和拉力传感器测量装置[4]等。这些方法都有一个共同点，都是基于位移式传感器感知车身结构的变化，从而测量出车辆的载重。因车身结构的变化主要是由于钢板弹簧的变形产生的，因此，对钢板弹簧分析的准确与否直接影响到汽车载重测量信息的准确性。现代学者们通过对钢板弹簧的分析，提出了几种计算方法，如：共同曲率法[5]、集中载荷法[6]和主片分析法[7]等。这些方法虽然都能计算板簧刚度的近似解，但其求得的汽车载重误差比较大。而应用有限元技术，能够准确的模拟出钢板弹簧在工作过程中所受到的各种因素，包括板簧的大变形和簧片间的接触等。

为了分析钢板弹簧的刚度和应力分布，许多学者都对其进行研究，其中，文献[8]研究了钢板弹簧的摩擦特性，文献[9]采用有限元分析了钢板弹簧的迟滞特性，文献[10]采用有限元分析了钢板弹簧的刚度特性，文献[11]等利用有限元分析了针对某汽车后悬架钢板弹簧的静态强度特性。

由于采用位移式传感器测量汽车载重时，位移传感器只能感知钢板弹簧的变形量，而板簧各片间存在着摩擦，其刚度特性复杂，所以通过计算钢板弹簧刚度以求得的变形与载重是有误差的。为解决上述问题，提出一种基于应变传感器的汽车载重系统，在钢板弹簧上安装应变传感器，利用有限元方法模拟钢板弹簧的工作状况，通过所测应力值来获得其所承受的载荷量。汽车的载荷不仅包括静态载荷，还包括汽车车身驾驶过程中产生的动态载荷，自载重测量系统主要是测量静态载荷，如果汽车在行驶过程中振动小，则简化为静态载荷，如果振动过大，则会产生动态载荷。因此，为了获得汽车的载重量，需对钢板弹簧进行静动态特性研究。

2 传感系统工作原理

2.1 载重测量工作原理

由于主要当汽车受到载荷作用时，钢板弹簧产生变形，在这一过程中，钢板弹簧可等效于悬臂梁，集中力作用下的悬臂梁模型，如图1 所示。

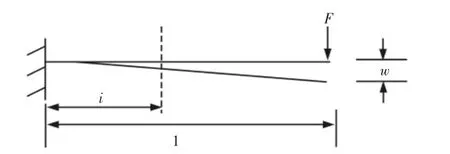
图1 集中力作用下的悬臂梁模型Fig.1 Cantilever Beam Model Under Concentrated Force

根据材料力学原理，集中力作用的悬臂梁挠度方程及x 截面处的弯矩方程分别为：

式中：ω—挠度；F—集中力；x—集中力与固定端的距离；E—弹性模量；I—截面惯性矩；l—悬臂梁长度；M—弯矩。

又因应力与应变关系式为：ε=σ/E，而矩形截面梁上的最大正应力为σMAX=M/WZ，因此截面x 处梁表面上的应变与弯矩的关系为：Mi=WZEεi，因此悬臂梁的挠度方程可写为：

式中：εi—i 处的应变值；h—矩形截面梁的高；WZ—抗弯截面系数；I—截面惯性矩。

因此只需测得i 处截面梁表面上的应变值，便可求出梁上任意x 处的挠度值，再根据有限元分析得出的钢板弹簧上载荷与形变的关系，可求出单个板簧所承受的汽车载荷。

2.2 应变传感器的安装

应变传感器的安装结构图，如图2 所示。

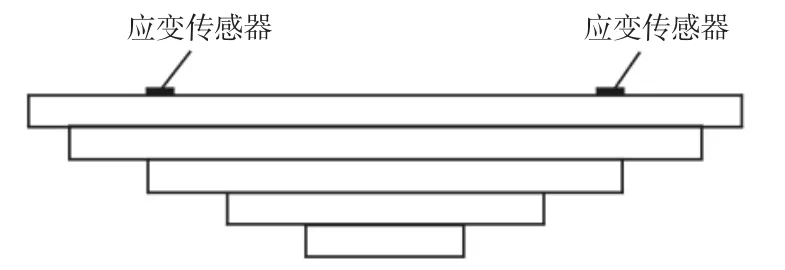
图2 车载式应变传感器安装示意图Fig.2 Vehicle-Mounted Strain Sensor Installation Diagram

在载荷作用下，汽车的钢板弹簧产生变形，使得应变传感器数值发生变化。预先标定出传感器电路输出电压值与该板簧载荷值之间的关系，就可根据各传感器电路的电压值得到该板簧的载荷质量。将各板簧的载荷量采用“加权求和”的方法，得到汽车的载荷量。

在实际过程中，为了能够准确得到汽车载重测量的信息，需要对其钢板弹簧进行分析，在不同影响因素下分析其对汽车载重测量系统的影响。

3 钢板弹簧静态特性的有限元分析

3.1 模型的建立

某车型5 片等截面对称的钢板弹簧模型，其半长模型，如图3 所示。

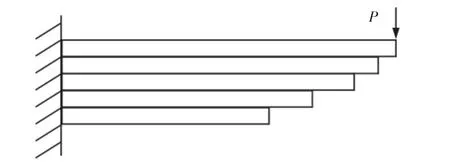
图3 钢板弹簧的半长几何模型Fig.3 Semi-Long Geometric Model of Leaf Spring

钢板弹簧的具体几何尺寸，如表1 所示。在建模的过程中，由于钢板弹簧具有对称性，故只需对钢板弹簧的一半进行分析即可。

表1 钢板弹簧各片的几何尺寸Tab.1 Geometrical Dimensions of Each Leaf Spring

3.2 模型的计算结果分析

在满载的条件下摩擦系数为0.1、0.15、0.2 的Von-Mises 等效应力云图，如图4 所示。

图4 不同摩擦系数条件下的最大等效应力云图Fig.4 Maximum Equivalent Stress Cloud Diagram Under Different Friction Coefficients

通过仿真得出的最大等效应力值，如表2 所示。

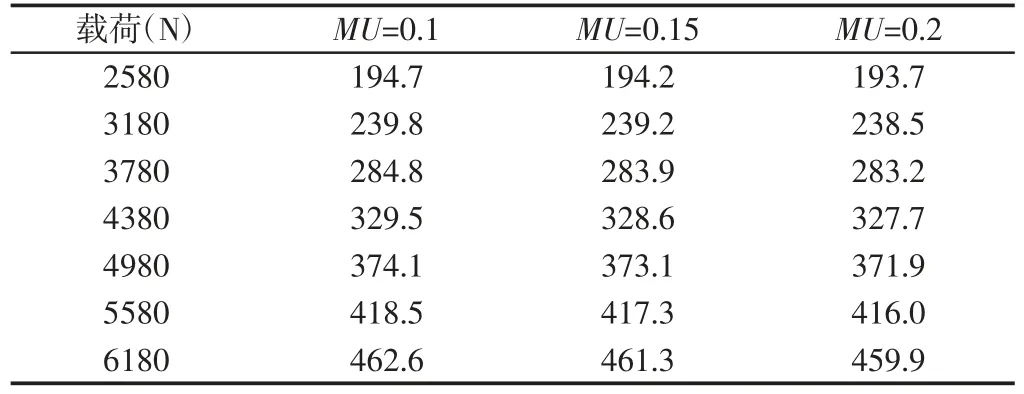
表2 不同摩擦系数和不同载荷条件下的最大等效应力值（单位：MPa）Tab.2 Maximum Equivalent Stress Value Under Different Friction Coefficients and Different Load Conditions（MPa）

从图4 中分析得到的等效应力云图可以看出，在不同摩擦系数条件下，钢板弹簧的应力分布范围大致相同。

从表2 可以看出，随钢板弹簧簧片间摩擦系数的增大，其最大等效应力值减小，但这种减小量在（0.2～0.3）%，即随摩擦系数的变化，簧片间的应力变化小，基本可忽略，所以应用应变传感器能够有效的测量出钢板弹簧的应力值。

不同摩擦系数分别0.1、0.15、0.2 在满载的条件下的位移云图，如图5 所示。

图5 不同摩擦系数条件下的最大变形云图Fig.5 Maximum Deformation Cloud Diagram Under Different Friction Coefficients

从图5 可以看出，在不同摩擦系数条件下，悬臂端的位移也不同。通过仿真得出的变形量，如表3 所示。由表3 可以看出：在相同载荷条件下，随钢板弹簧簧片间摩擦系数的增大，其端部变形量减小，但这种减小量在（0.3～0.4）%，即随摩擦系数的变化，簧片端部变形量变化小，基本可忽略，不影响钢板弹簧所受载荷与形变的关系。利用MATLAB 软件处理表3 中的数据，可得到钢板弹簧的刚度特性曲线图，如图6 所示。

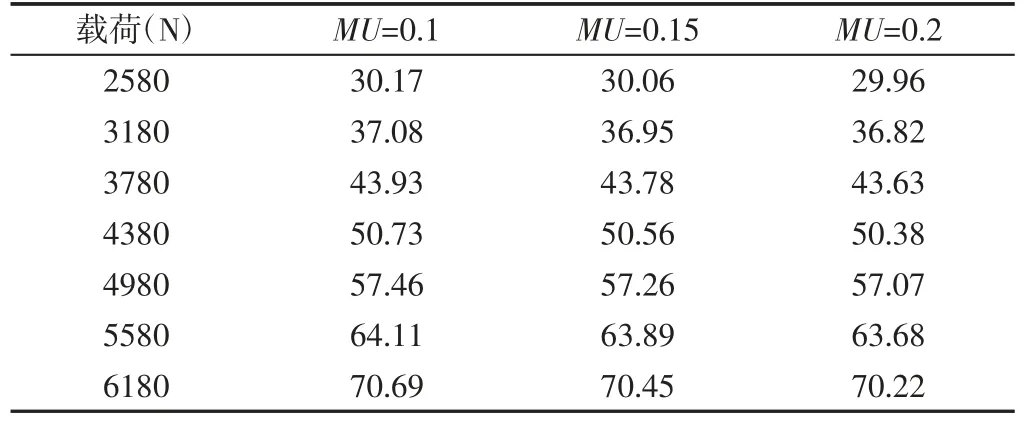
表3 不同摩擦系数和不同载荷条件下的变形量（单位：mm）Tab.3 Different Friction Coefficient and Deformation Under Different Load Conditions（mm）

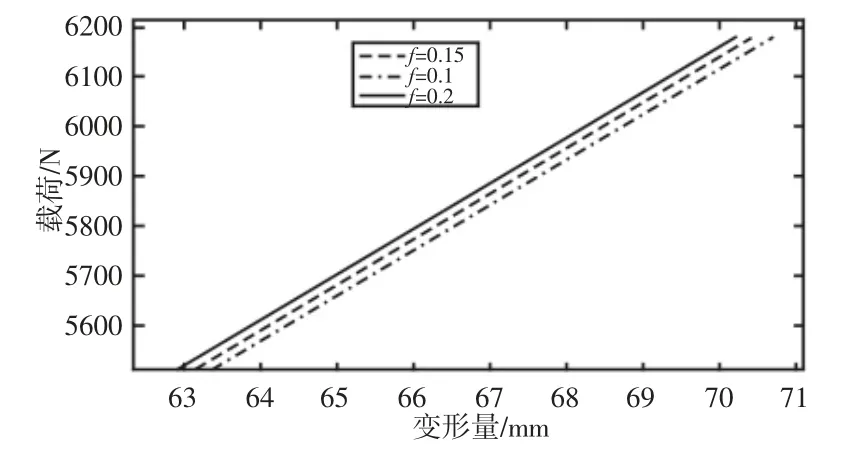
图6 不同摩擦系数条件下的钢板弹簧刚度特性曲线图Fig.6 Stiffness Characteristic Curve of Leaf Spring Under Different Friction Coefficient Conditions

由图6 可得出不同摩擦系数条件下的平均刚度值，如表4所示。

表4 不同摩擦系数条件下的平均刚度值Tab.4 Average Stiffness Value Under Different Friction Coefficients

从图6 可以看出，在不同摩擦系数下，钢板弹簧的载荷-位移曲线是线性的；在相同载荷下，摩擦系数越大，钢板弹簧的位移越小，说明摩擦系数越大，钢板弹簧的刚度也越大，但强度会降低。

当摩擦系数变化时，刚度变化量很小，说明板簧摩擦因素对应变传感器输出影响较小，不影响应变传感器的测量，即利用应变传感器能够有效的测量汽车的载重。

4 钢板弹簧动态特性的有限元分析

4.1 周期载荷下的迟滞特性

分析模型同静态分析模型相似，不同在于其钢板弹簧悬臂端施加的是一个正弦周期载荷，其载荷表达式为：

模型加载及其边界条件仍然采用静态分析时的加载方式和约束条件，利用有限元分析得到钢板弹簧的瞬态位移响应，摩擦系数为0.2 的载荷-位移曲线，如图7 所示。由图7 可以看出，在正弦载荷作用下，钢板弹簧的位移响应曲线滞后于载荷响应曲线，并且在加载和卸载过程中，都存在着一定的空隙，且在载荷极值处，空隙最大。板簧在正弦载荷作用下的载荷-位移曲线，如图8 所示。由图8 可见，在正弦载荷作用下，由于板簧间存在着摩擦，加载和卸载曲线不重合，导致加载和卸载过程中的动刚度不同，形成如图8 所示的迟滞回线，即说明钢板弹簧自身存在阻尼，表现为钢板弹簧的非线性和迟滞特性，图中曲线所包围的面积即钢板弹簧簧片间摩擦力所做的功。

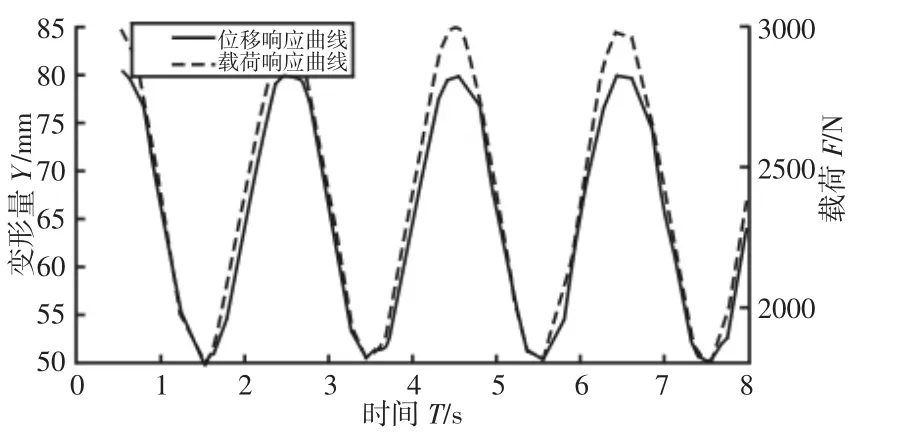
图7 钢板弹簧正弦载荷与位移响应曲线Fig.7 Sinusoidal Load and Displacement Response Curveof Leaf Spring

图8 正弦载荷作用下的载荷-位移图Fig.8 Load-Displacement Diagram Under Sinusoidal Load

钢板弹簧所产生的迟滞特性可以看作是在线弹性系统中加入相应的阻尼元件，阻尼元件的引入会影响汽车自载重测量的准确性，为了了解各因素对迟滞特性的影响程度，须对钢板弹簧进行参数性研究。

4.2 迟滞特性对汽车载重的影响

根据文献[9]，假设钢板弹簧在一个周期内形成的阻尼用阻尼系数为K 的速度阻尼来等效，则该速度阻尼消耗的功为：

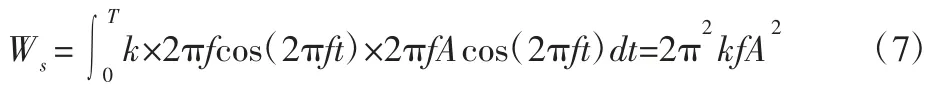
根据Ws=Wf，可得：

设在加载和卸载过程中产生的载荷差为ΔF0，且该载荷差值随变形线性变化，则WF=2AΔf0，得出：

式中：Ws—速度阻尼消耗的功；Wf—摩擦阻尼消耗的功；T—周期；K—等效阻尼系数；f—频率；A—振幅；ΔF0—载荷差。

式（9）说明钢板弹簧的等效阻尼与加载和卸载过程的载荷差值成正比，与激振振幅都成反比。通过对上述仿真分析可知，钢板弹簧簧片间的摩擦是导致迟滞特性产生的主要原因，也是影响汽车载重测量的主要原因。

为了减小摩擦特性对汽车载重测量的影响，该汽车载重测量系统的使用范围通常是在钢板弹簧簧片间静摩擦因数为（0.2～0.3），动摩擦因数为（0.15～0.2）之间，这样摩擦因数对汽车载重测量影响较小。

5 结论

（1）通过对钢板弹簧的静态仿真可以得出，当钢板弹簧簧片间的摩擦系数发生变化时，板簧簧片的应力值和刚度也会发生变化，则根据汽车载重测量的原理，当应力值和刚度改变时，汽车测量的载重也会改变，但从上述仿真结果可以看出，摩擦系数对板簧的应力值和刚度影响较小，不影响汽车载重的测量。

（2）通过对钢板弹簧的动态仿真可以看出，由于簧片间存在摩擦，导致钢板弹簧产生迟滞特性，摩擦越大，迟滞特性也就越明显，等效阻尼也就越大，导致汽车载重测量误差偏大，通常采用软件补偿的方法来减小板簧的迟滞特性。

（3）应变式汽车载重测量装置结构简单、测量电路简单、抗干扰性好、体积小、造价低等特点，在性能方面重复性误差及非线性误差较小，具有良好的使用前景。