铁磁性材料的脉冲涡流测厚与特征量提取

王安泉,陈健飞,杨 勇,韩 庆,宫 昊,闫泰松

(1.中国石油化工股份有限公司胜利油田分公司技术检测中心, 东营 257000；2.胜利油田检测评价研究有限公司, 东营 257000)

承压设备在使用过程中会因冲刷和腐蚀作用出现壁厚减薄的情况，当壁厚减薄到一定程度时会突然发生爆裂，进而对人员和外部环境造成严重伤害，因此为了保障承压设备的安全运行，减少爆裂情况的发生，需定期对其剩余壁厚进行检测[1-2]。脉冲涡流检测具有传统涡流检测的非接触、成本低、对人身和环境无危害等特点，并且脉冲信号具有宽频谱的特性，又使得脉冲涡流检测具有穿透能力强、检测速度快、漏检率低等特点，因此其被广泛应用于金属的缺陷和厚度的检测中[3-4]。脉冲涡流检测中一个至关重要的工作是提取检测信号中剩余壁厚的特征量，而脉冲涡流检测信号中包含着众多的频谱信息，特征量提取时存在一定困难。陈兴乐等[5]以有限厚导体与无限大导体之间的感应电压差峰值时间作为特征量，实现了铝板厚度测量；王志春等[6]分别从时域和频域提取特征值，针对不同电导率层，给出了相对较适合的特征值；刘丽冰等[7]以时域信号峰值、过零时间及上升时间为特征量实现了缺陷的分类识别；GIGURE等[8]指出提离交叉点不受传感器提离高度的影响，可以用于缺陷定量、裂纹检测；柯海等[9]的研究表明峰值、峰值时间、过零点、提离交叉点等特征量难以适用于铁磁性试件的测厚，并提出了基于信号斜率的测厚方法。由于铁磁性材料磁导率的不均一性和非线性，故特征量的提取更加困难且研究较少，因此文章开展了提取铁磁性材料测厚特征量的研究，仿真试验结果表明，可以使用差分电压信号峰值、差分电压信号峰值时间及单对数坐标系下晚期信号斜率为特征量来测量铁磁性材料的壁厚。

1 脉冲涡流测厚的基本原理

将激励线圈放置在被测试件上方，在其两端加载一定幅值、频率和占空比的脉冲信号，由法拉第电磁感应定律可知，当脉冲信号发生跳变时会在激励线圈周围感生出快速衰减的磁场B1，变化的磁场B1又会在被测试件中感应出变化的涡流(脉冲涡流)，在脉冲涡流向着被测试件内部进行扩散衰减时会在其周围产生另一个变化的磁场B2，通过检测线圈检测磁场B2的变化并转换为随时间变化的电压信号，当试件厚度发生变化或者存在缺陷时，对应的检测信号也不相同，因此通过对检测信号进行分析和特征量提取，找到特征量与被测试件厚度的关系，就能实现壁厚的测量[10]，脉冲涡流的测厚原理如图1所示。

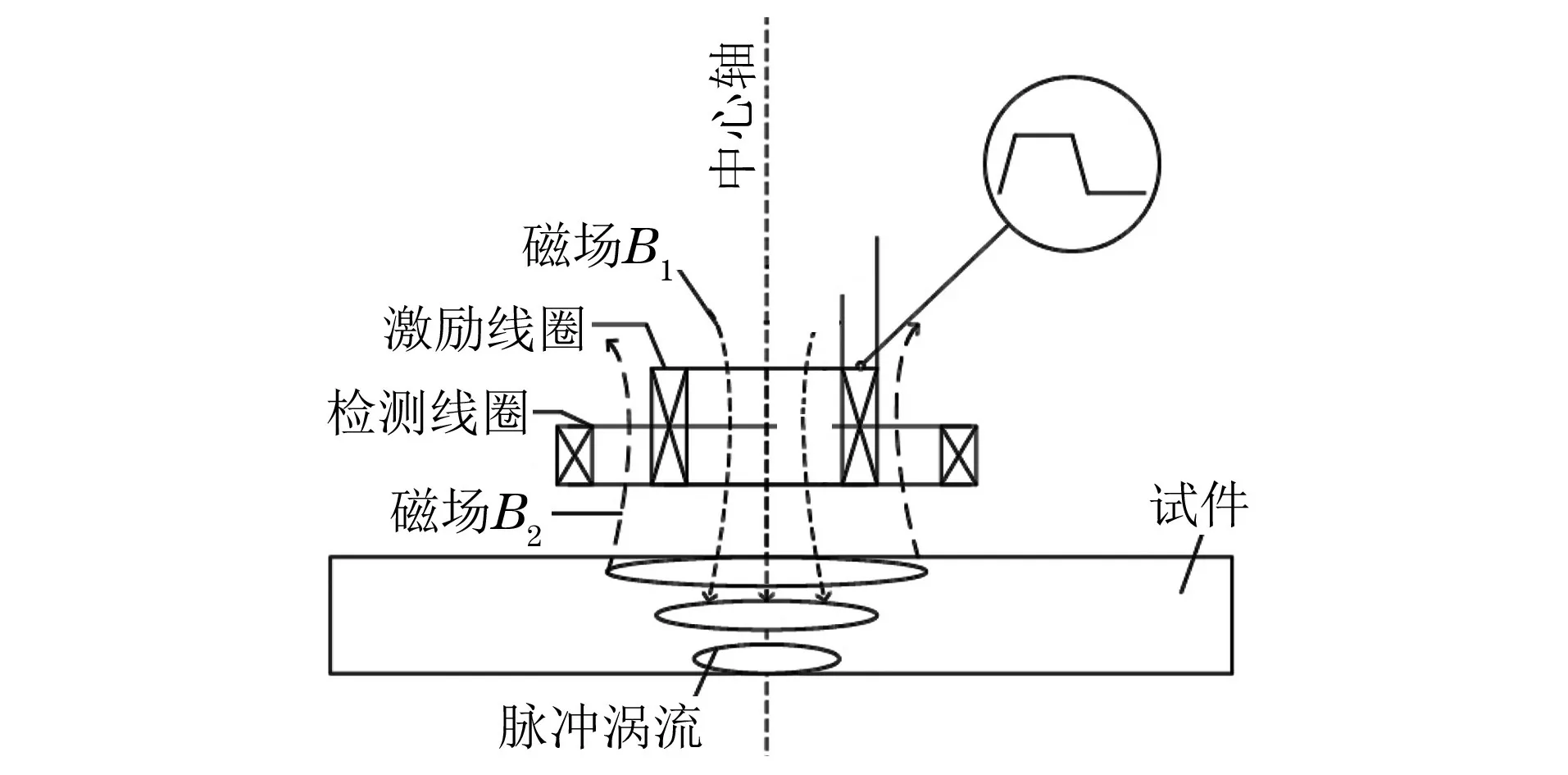
图1 脉冲涡流测厚原理示意

2 有限元建模与仿真

2.1 有限元仿真模型的建立

根据脉冲涡流检测原理并结合实际情况，使用COMSOL Multiphysics软件建立了脉冲涡流测厚的仿真模型，整个模型包括激励线圈、检测线圈、被测试件(Q235钢板)及空气域，激励线圈和检测线圈均为空心圆柱形结构，两个线圈同轴放置，激励线圈在内，检测线圈在外。为简化模型，以厚度均匀的钢板替代管道作为被测试件，由于模型具有对称性，同时为了减小计算量，故将三维的仿真模型转化为二维的仿真模型，脉冲涡流测厚的二维仿真模型如图2所示。

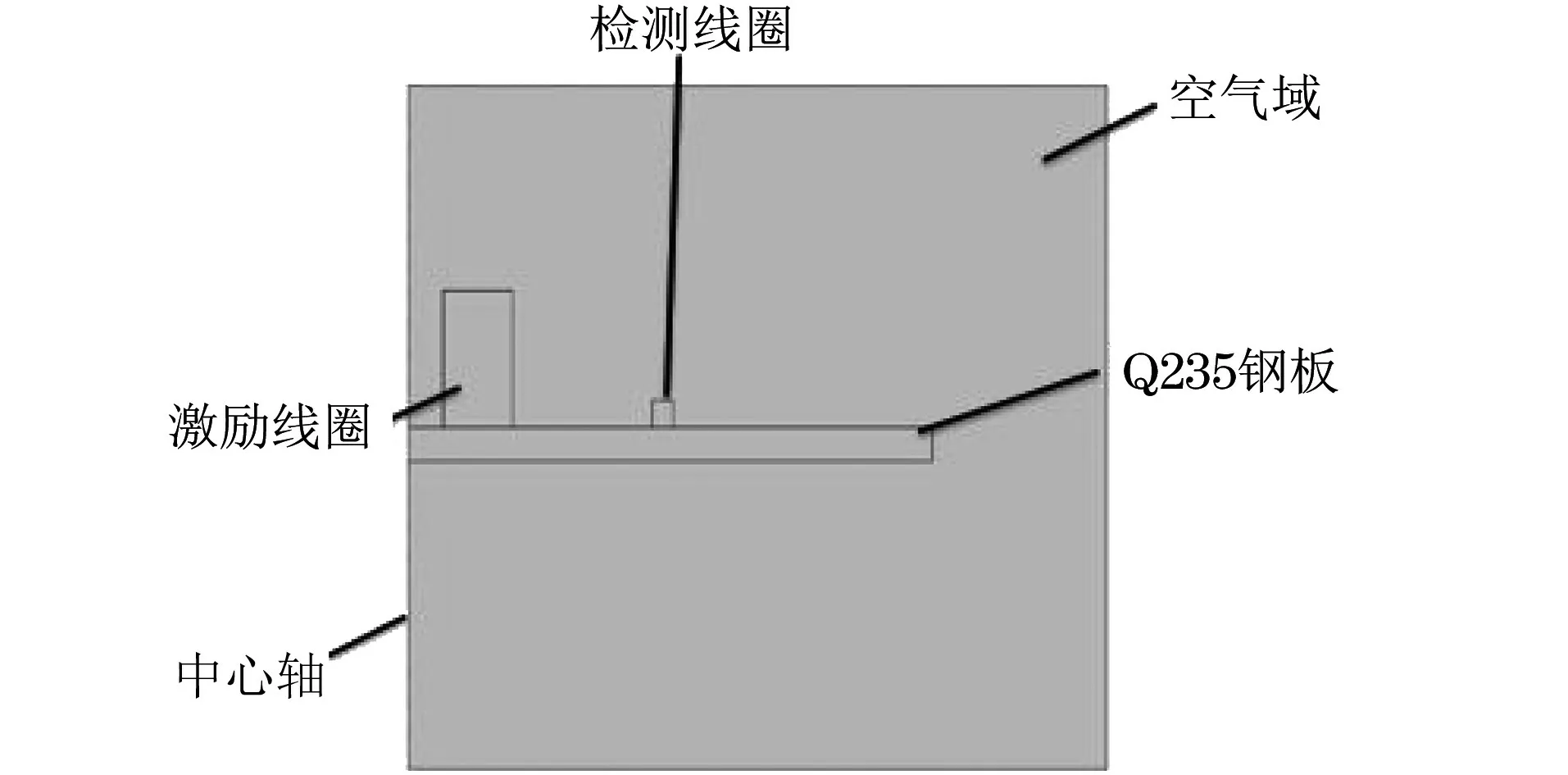
图2 脉冲涡流测厚的二维仿真模型

2.2 仿真参数的选取

测厚模型中的激励线圈和检测线圈与被测试件之间无提离，激励线圈、检测线圈及脉冲激励的参数如表1所示，被测试件及线圈导线的参数如表2所示。

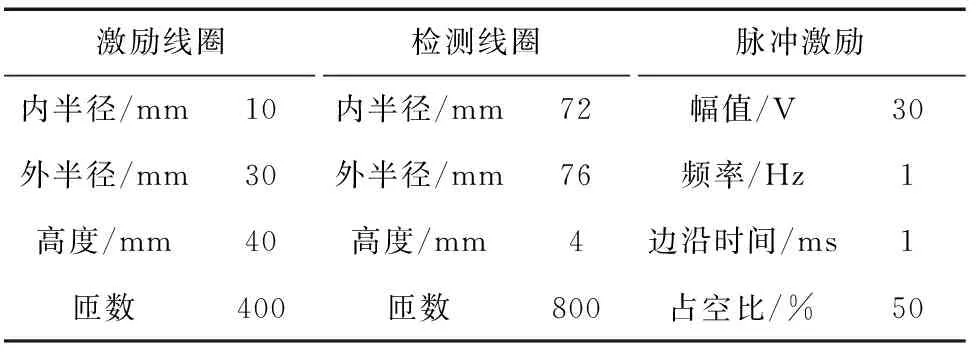
表1 仿真试验参数

表2 被测试件及线圈导线参数

模型区域采用自由网格进行划分，计算求解时选用瞬态求解器，求解步长为0.01 ms，求解终止时间为500 ms。11 mm厚试件的仿真检测信号如图3所示，只需要找到检测信号中特征量与被测试件厚度的关系，即可实现对被测试件厚度的测量。

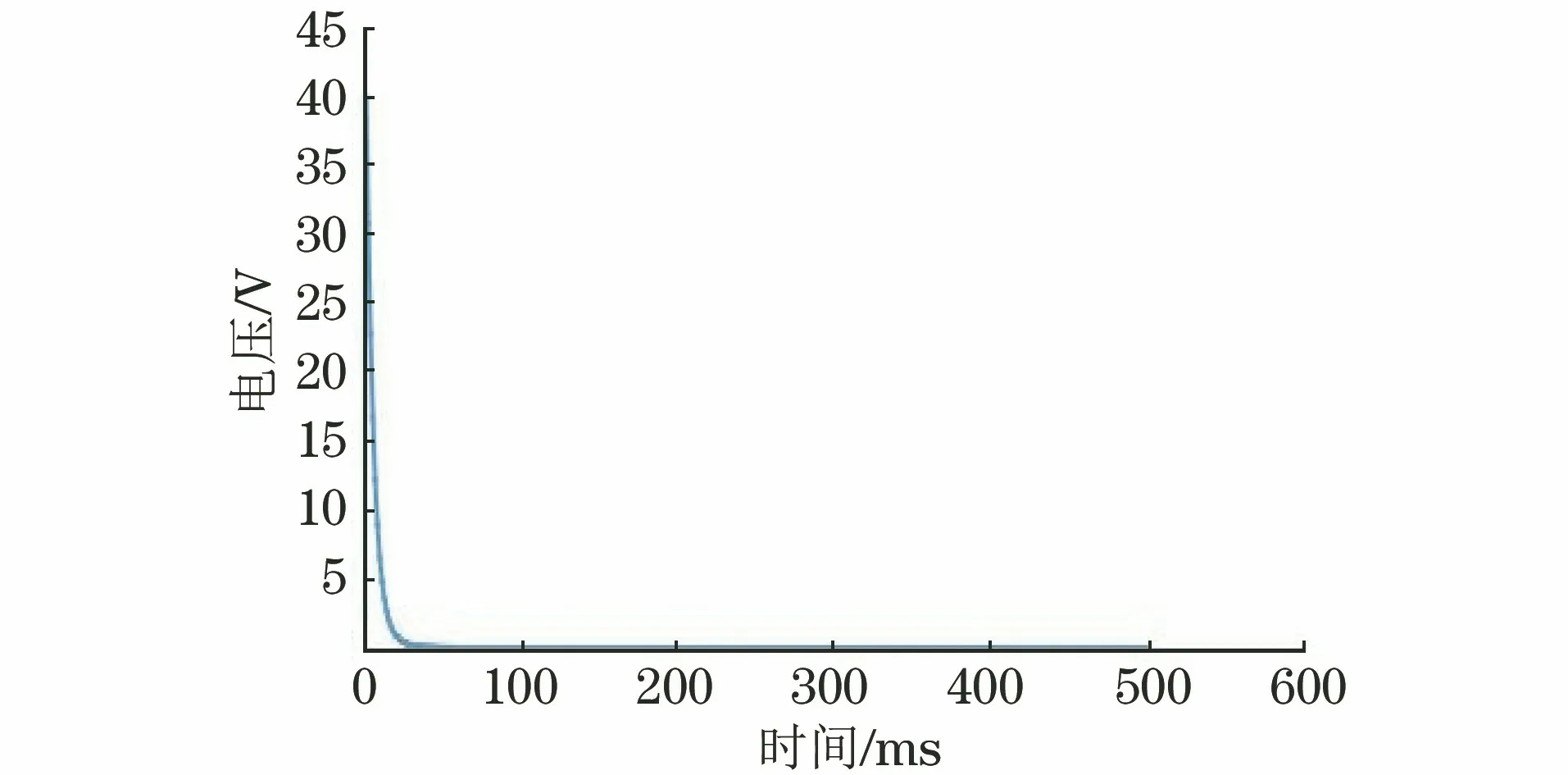
图3 11 mm厚试件的仿真检测信号

3 数据处理与特征量提取

3.1 差分电压信号

通过仿真试验得到了420 mm厚试件的检测信号，将厚度为11，20 mm的检测信号绘制在同一直角坐标系下(见图4)，由图4可以看出厚度越大信号衰减得越慢。

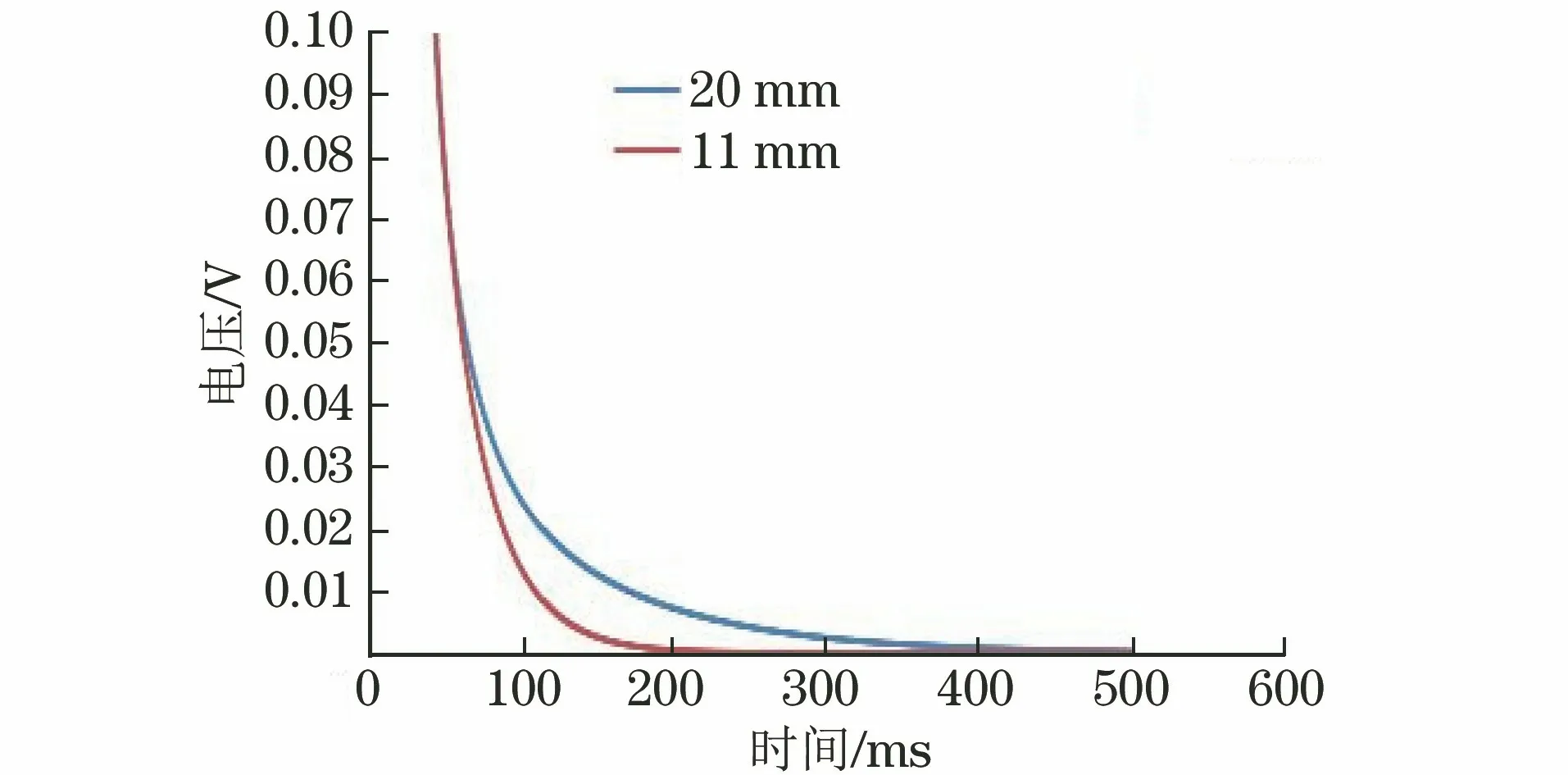
图4 11,20 mm厚度试件的仿真检测信号

以厚度20 mm处的检测信号为参考信号，用参考信号减去检测信号得到的就是差分电压信号[11]，不同厚度所对应的差分电压信号如图5所示，从图5中可以看出，差分电压信号曲线有两个重要的特征，分别差分电压信号峰值和差分电压信号峰值时间。

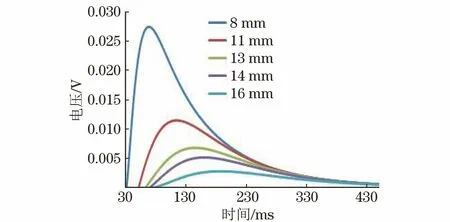
图5 不同厚度试件对应的差分电压信号

3.2 基于差分电压信号峰值的壁厚测量

从图5中可以看出，厚度越小则差分电压信号峰值越大，不同厚度对应的差分电压信号峰值如表3所示，将表中数据绘制在直角坐标系中得到差分电压信号峰值-厚度曲线(见图6)，使用MATLAB软件对差分电压信号峰值和厚度进行拟合，发现在417 mm厚度内差分电压信号峰值与厚度呈现较好的幂函数关系，二者的关系式如式(1)所示(式中x1,y1分别为差分信号峰值与试件厚度)，因此可以得出结论，以差分电压信号峰值为特征量能够测量的厚度范围为417 mm，但差分信号峰值均为毫伏级，在实际应用中检测易受噪声干扰，使得检测准确度降低，所以该技术不适用于工程应用。

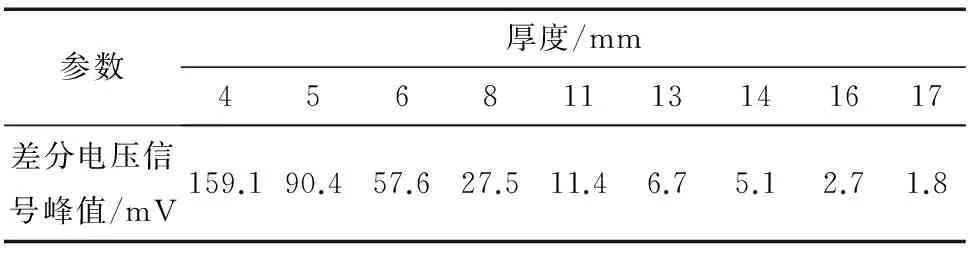
表3 不同试件厚度对应的差分电压信号峰值

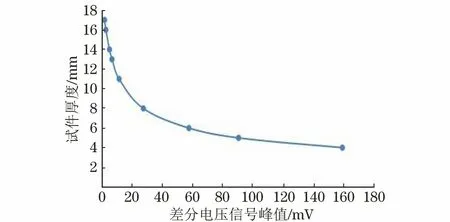
图6 差分电压信号峰值-厚度曲线

(1)

3.3 基于差分电压信号峰值时间的壁厚测量

从图5中可以看出，试件厚度越大则差分电压信号的峰值时间越大，不同厚度对应的差分电压信号峰值时间如表4所示，将表中数据绘制在直角坐标系中得到差分电压信号峰值时间-厚度曲线(见图7)，使用MATLAB软件对差分电压信号峰值时间和厚度进行拟合，发现在417 mm厚度内差分电压信号峰值时间与厚度呈现较好的线性关系，二者的关系式如式(2)所示(式中x2,y2分别为差分电压信号的峰值时间与试件厚度)。

y2=0.071 32x2+2.737

(2)

表4 不同试件厚度对应的差分电压信号峰值时间

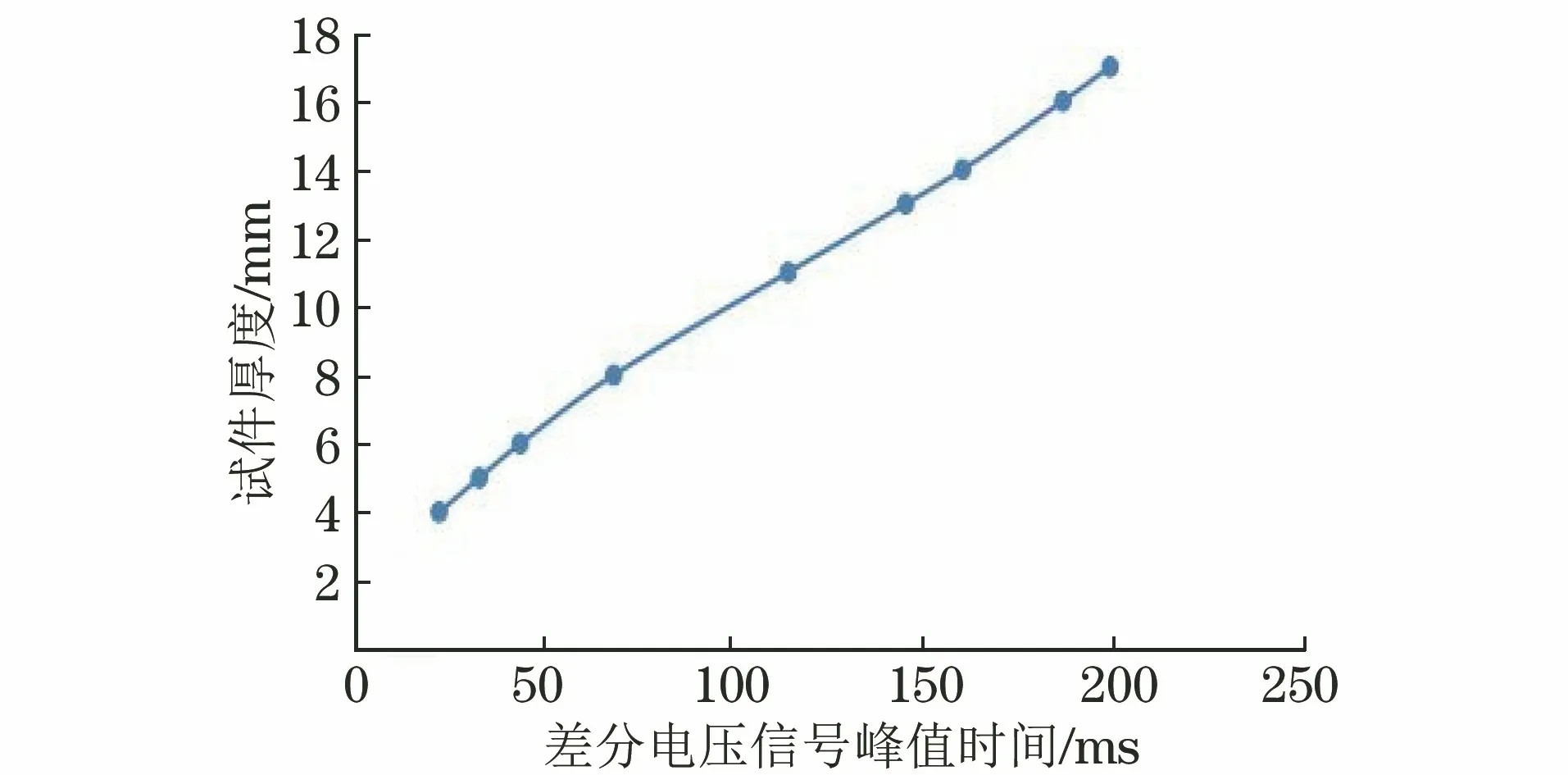
图7 差分电压信号峰值时间-厚度曲线

因此可以得出结论,以差分电压信号峰值时间为特征量能够测量的厚度范围为417 mm，但在实际检测过程中,该特征量存在提取困难的弊端，亦不适用于工程应用。

3.4 基于单对数坐标系下晚期信号斜率的壁厚测量

通过仿真试验得到了1.545 mm厚试件的检测电压信号，观察可以发现峰值之后的晚期电压信号时域变化规律不同，使用峰值后的信号，将不同厚度的检测电压信号绘制在单对数坐标系中(见图8)，从图8中可以看出不同厚度所对应的晚期信号斜率不同，不同厚度所对应晚期信号斜率如表5所示，结果显示，424 mm内的厚度与晚期信号斜率呈现幂函数关系，晚期信号斜率-厚度曲线如图9所示，使用MATLAB软件对晚期信号斜率(x3)和厚度(y3)进行拟合，得到二者的关系如式(3)所示。

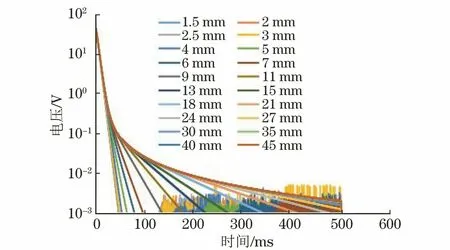
图8 单对数坐标系下的检测电压信号

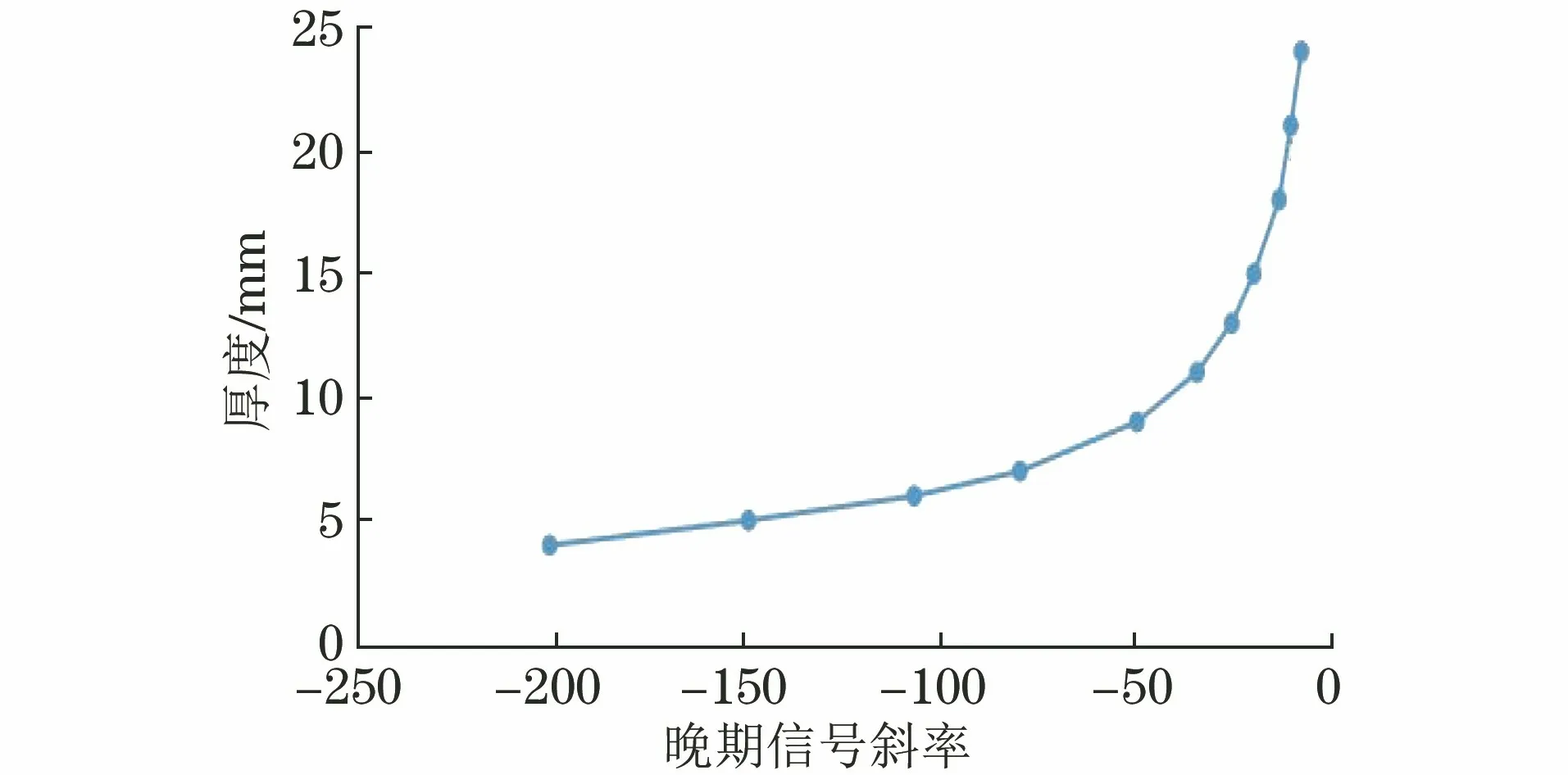
图9 晚期信号斜率-厚度曲线

表5 不同试件厚度对应的晚期信号斜率

y3=71.71(-x3)-0.53

(3)

因此可以得出结论，以晚期信号斜率为特征量能够测量的厚度范围为424 mm，而噪声导致的局部畸变信号可以通过信号处理的方式来剔除，对斜率特征影响较小，因此晚期信号斜率这一特征量对于脉冲涡流测厚技术具有较大的工程应用价值。

4 结语

使用有限元法建立了铁磁性材料的脉冲涡流测厚的仿真模型，获得了不同厚度铁磁性材料所对应的检测电压信号，对信号进行分析和特征量提取后得知，以差分电压信号峰值、差分电压信号峰值时间和晚期信号斜率为特征量能测量壁厚，以差分电压信号峰值为特征量能够测量的厚度范围为417 mm，以差分电压信号峰值时间为特征量能够测量的厚度范围为417 mm，以晚期信号斜率为特征量能够测量的厚度范围为424 mm，但由于差分电压信号峰值为毫伏量级，差分电压信号峰值和峰值时间的提取较为困难，故在实际检测过程中，多以晚期信号斜率为特征量来反演壁厚。