笔算加法中进位错误的解决策略

□李小明

从二年级初学笔算加法到中高段练习多位数加法，不少学生会出现一种“平凡又频繁”的错误：满十不进一或知道进一却漏加。二年级的两位数加两位数笔算是笔算的起始课，是种子课，起着“筑基”的重要作用。因此笔者通过实践与思考，提出以下解决策略。

一、激活“内需”

在学习笔算前，学生会用口算解决计算问题。两位数加两位数，大部分学生能通过数的分解、组合，口算出得数。如果要求用笔算计算，学生需求不强，反而认为麻烦。教学时教师可以出示多数位的复杂题目，让学生从内心感受到竖式计算的必要。

比如在课始教师可以出示“2126+472”，提问：“你能口算出它的得数吗？”“看到这样的题目你有什么感觉？”学生可能会说眼睛都看花了。教师首先引导学生思考有没有好办法能够让自己看得不那么累且可以轻松计算？然后请学生将该题列成竖式进行计算。学生感受到竖式真是解决复杂计算题的好助手，激发起学习竖式的需求。

复杂的多位数加法由于位数多，要对各个数位上的数进行组合，学生很容易看错数，口算起来并不方便。教师通过提问，启发引导学生思考如果将两个数数位对齐排列就能很方便地算出得数。

二、亲历过程

口算和笔算虽然都是按照相同单位的数相加的算理进行计算，但记录方式有所不同。口算的记录是一次完成，两位数加两位数笔算的记录要分多次完成。教学时如果缺少对口算与笔算的沟通，学生面对笔算也就无从下手，或仍用口算算出得数后一次记录完成。

如教学“34+25”，学生在经历用小棒、图形摆的过程后，教师引导学生看图说说是怎么算出得数的。教师先按照学生的表达做好记录：①30+20=50，4+5=9，50+9=59；②4+5=9，30+20=50，50+9=59。再引导学生说说怎样才能把思考过程方便地记录下来。学生尝试用竖式记录时可能会出现两种不同的方式：从低位开始记录或从高位开始记录。这时教师应引导学生将笔算记录与口算过程进行有效对接（见图1），让笔算的算理可视化，使学生感受到笔算就是把口算的过程一步步记录下来的计算，并理解为什么要这样记录，知其所以然。

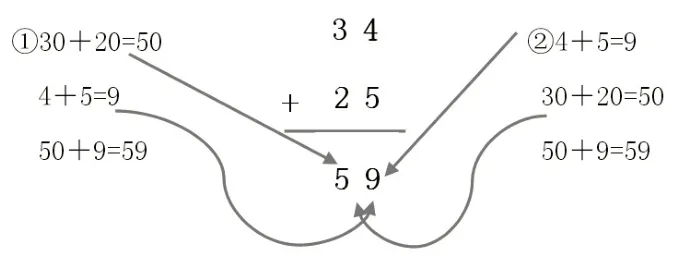
图1

三、构建模型

数形结合不仅是一种重要的数学思想，也是一种常用的数学方法。竖式对比横式，其特点是相同单位对齐，计算时不需要对数进行重新组合。学生是否理解竖式的这一特点，体会到它的方便呢？后测中仍会看到部分学生对竖式感到茫然：竖式是怎么来的？怎样依据竖式想象实物图呢？所以建立竖式模型十分重要。

如在教学两位数加两位数（不进位加）的引入环节，教师可以直接出示“34+25”让学生口算，然后思考用小棒可以怎么摆。接着教师呈现图2，提问：“怎样摆小棒可以较快地数出小棒的数量？”学生回答：“整捆和整捆的放在一起，单根和单根的放在一起。”教师呈现图3，提问：“除了用小棒表示数，还可以用什么来表示呢？”学生交流后教师呈现图4、图5。最后由直观图抽象出竖式，再让学生看图说说竖式的计算方法。

在这个过程中，教师放慢节奏，让学生经历竖式的抽象过程，建立竖式模型的表象。

四、加深表象

教育心理学家认为儿童的认识按照“动作思维—表象思维—抽象思维”的路径发展。教学笔算两位数加两位数（进位加）时，教师让学生摆小棒感知算理，当单根小棒数合起来超过十时，需把10根扎成一捆，把这一捆放到整捆的小棒中，学生依据操作抽象出竖式算法。这样的教学符合学生的认知规律，然而在教学中笔者发现，仅有25%的学生能完成这样的操作，说明学生对于单根小棒满十根要扎成一捆的意识不强。教学时能否用一种载体迫使学生采用个位相加满十了必须向十位进“1”的操作？笔者使用了计数器。

比如教学28+45，引导学生借助计数器来算。

师：28加45我们除了可以用小棒来摆，还可以用计数器来算。请同学们在自己的计数器上拨一拨、算一算。大家想一想，先拨几，再拨几呢？

生：我先拨出28，然后十位上再拨4，个位上再拨5，8加5满十向十位进“1”，个位上是3，十位上就是7，所以结果就是73。

生：我先拨出28，然后拨5个，个位满十向十位进“1”，个位上拨3，十位上再拨4个，最后2+1+4=7，所以是73。

师：不管怎么拨，你们发现它们有什么共同的地方了吗？

生：十位和十位的数拨在一起，个位和个位的数拨在一起。

生：个位相加满十，都要向前一位进“1”。

教师顺势引导学生将拨珠子的过程用竖式记录下来。

计数器形象直观，学生通过动手拨一拨，加深了对满十进“1”的认识，突破了教学的难点，也为后面教学多位数笔算进位加法做了铺垫。

五、主动建构

由于看书、写字一般都是按照从左往右的顺序进行，所以笔算时，学生也习惯从左往右进行记录，哪怕是进位加时，还依然从左往右计算。如何让学生体会到笔算加法从低位加起的简便，并主动改变习惯，从低位开始算起，形成算法呢？教学时如能让学生比较与交流这两种笔算的方法，体验到从右往左计算的方便，学生便能领会竖式计算从低位算起的必要性。

如教学28+45时，学生拨计数器记录操作过程，有的学生先算十位2+4，在十位上记6，再算个位8+5=13，个位上写3后，发现高位写6不对，于是擦去6改成7；有的学生算好2+4=6后不急着记录,先看一下个位相加是否满十，然后在十位上写7，最后在个位上写3；还有的学生先算8+5=13，先在个位上写3再向十位进“1”，接着算2+4+1=7。交流时，教师引导学生比较从高位算起和从低位算起这两种方法。学生在对比中感受到从高位算起，记录起来很麻烦要涂改，如果从低位算起就可以直接写得数了，最后得出“两位数加两位数从低位算起”的结论。

六、形成技能

练习是形成技能的重要一环。两位数加两位数进位加的笔算学生易出现个位相加满十不向前进“1”的情况或进“1”却忘了加上去的错误，因此教师应该设计有针对性的练习，以提高计算练习的实效性。

如学习进位加后可进行以下题组练习。题1是从一位数加一位数的进位加、两位数加一位数的进位加一直到两位数加两位数的进位加，使学生通过练习发现题组中个位都有“7+6”，计算时都要向十位进“1”。题2是让学生说说五角星下藏着的数是几。需要学生思考“个位两个数相加是否满十”。题3引导学生有序思考问题，进一步思考个位相加是否满十，在确定十位上数的时候应考虑进位“1”。

1.笔算下列各题，并说说你发现了什么？

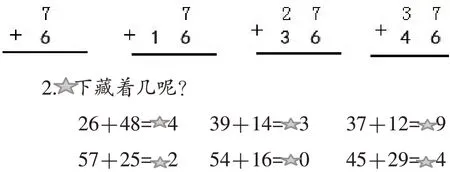
3.竖式中的图代表几呢？想想可以从哪里先思考。

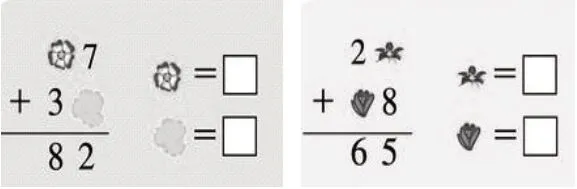
针对性的练习既可以“治病”，又可以“防病”，有的学生作业求快、字迹潦草、练习后不检查，导致数字抄错、运算符号看错、计算出错等，所以教师还应培养学生良好的笔算习惯，要求学生做到以下几点:①看清数字与符号，专心计算；②书写工整、格式规范；③算好后要验算、检查。教师对学生的检查要给予方法上的指导，如一步一回头式的检查、交换加数的位置重新算一遍、估一估等，帮助学生养成检查的习惯。