主成分回归方法解决实际问题

孙嘉聪 王飞 沈丹

【摘要】主成分回归是在确保丢失的有用信息最少的情况下，将多数原始变量转化成几个少数综合变量的一种降维回归方法.主成分回归能够很好地解决当样本数据存在一定程度的重复性并且在高维的空间中做分析时比较复杂的问题.它是一次对回归自变量重新选择的过程.

【关键词】主成分回归;主成分分析;特征值;贡献率

一、主成分回归的含义

主成分回归是根据降维的思想通过线性变换，将样本中的多个指标组合成少数几个相互独立的并且能充分反映总体信息的指标，在不丢掉重要信息的条件下避开了变量间的共线性问题，进而分析.

二、主成分回归的基本步骤

首先利用主成分分析得到自变量的主成分矩阵和各个主成分累计方差的百分比;其次根据累计方差的百分比大于百分之八十的原则，得到新的回归方程，再从得到的新的主成分回归方程中选出最佳标准化主成分回归方程;最后对最佳标准化方程中新的自变量、因变量做最小二乘估计转换成一般线性回归方程.

三、相关定义

样本数据标准化后，其相关阵的特征值为λ1≥λ2≥…≥λp≥0，φ1，φ2，…，φp为对应的单位正交特征向量，Var（Ri）=λi，i=1，…，p且Var（R1）≥Var（R2）≥…≥Var（Rp）.

贡献率：λl∑pi=1λi为主成分Zl的贡献率.

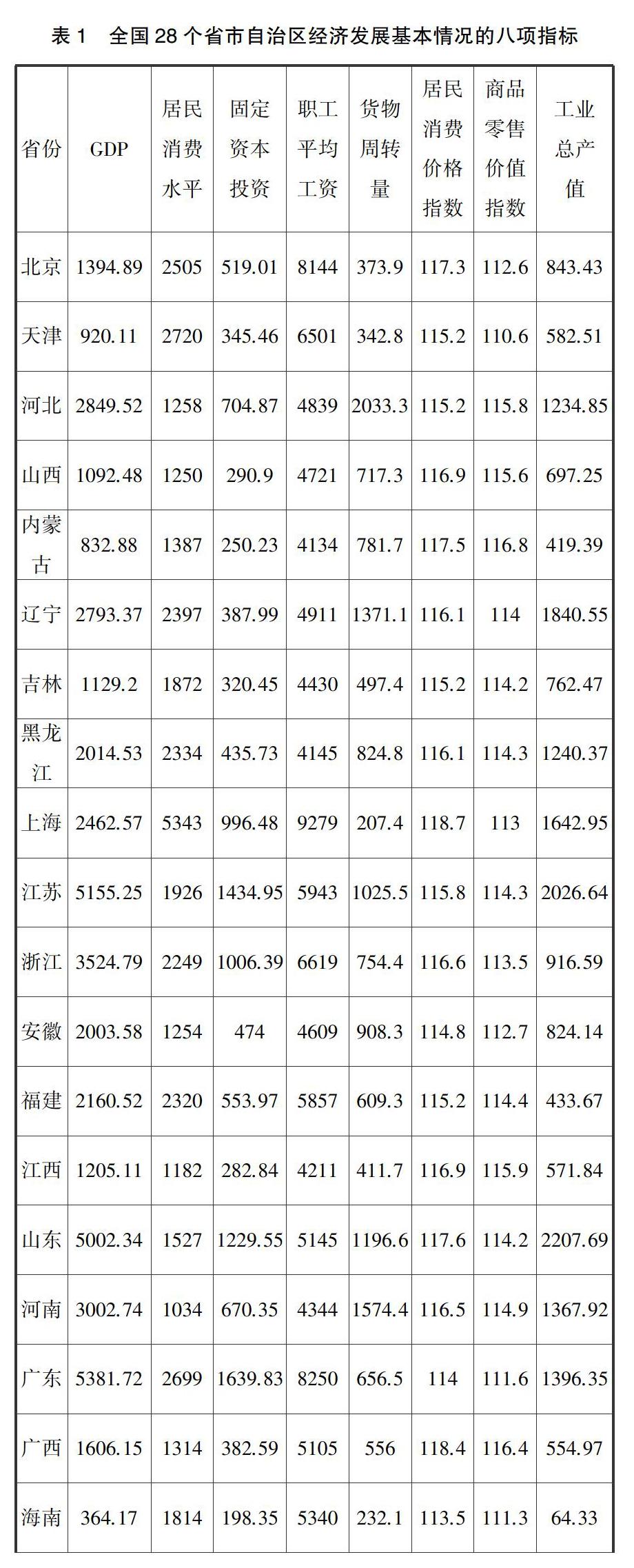
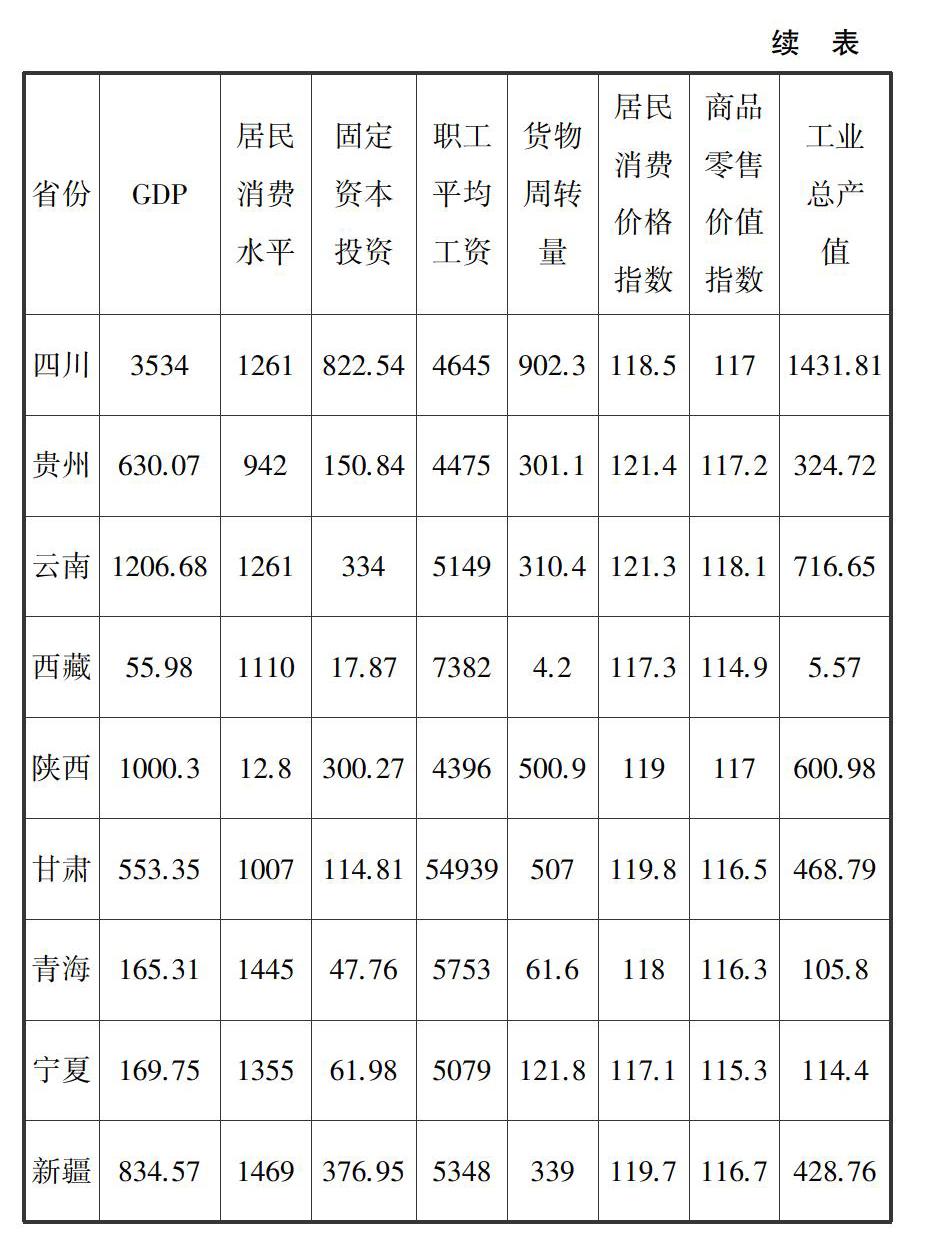
累计贡献率：∑qk=1λk∑mi=1λi为主成分Z1，Z2，…，Zq（q

均方误差：MSE（）=E（-θ）T（-θ）=E‖-θ‖2，其中为θ的一个估计.

四、实际应用

对全国28个省市自治区经济发展基本情况八项指标做主成分分析，数据如下：

求R的特征值及各特征值的贡献率

如图1所示前三个特征值累计贡献率已达89.5%，则前3个主成分基本包含了全部指标具有的信息，所以我们取前三个特征值，并计算出相应的特征向量.

α1=（0.4706410.4567080.424712-0.31944

0.3127290.2508020.240481-0.26267）T

α2=（0.1079950.2585120.2875360.400931

-0.404310.498801-0.488680.167392）T

α3=（0.192410.1098190.192410.397525

0.24505-0.247770.3321790.723351）T

即前三个主成分分别为：

F1=0.470641X1+0.456708X2+0.424712X3-0.31944X4+0.312729X5+0.250802X6+0.240481X7-0.26267X8

F2=0.107995X1+0.258512X2+0.287536X3+0.400931X4-0.40431X5+0.498801X6-0.48868X7+0.167392X8

F3=0.19241X1+0.109819X2+0.19241X3+0.397525X4+0.24505X5-0.24777X6+0.332179X7+0.723351X8

从第一个主成分表达式中可得知，前三项指标的系数比较大，起主要作用;我们可以把第一个主成分看成是前三项指标（GDP、居民消费水平、固定资本投资）反映经济发展状况的综合指标.

從第二个主成分表达式中可得知，第四、五、六、七项指标系数比较大，且第六、七项指标的影响尤其大，则将其看成四、五、六、七项（职工平均工资、货物周转量、居民消费价格指数和商品零售价值指数）的综合指标.

从第三个主成分表达式中可得知，第八项的指数影响最大，远超过对其他指标的影响，则可单独看成是工业总产值的影响.

由以上分析可知，主成分回归的主要目的是要提取隐藏在矩阵X中的相关信息，然后用于预测变量Y的值.这种做法可以保证让我们只使用那些独立变量，从而达到改善预测模型质量的目的.由于主成分之间的互不相关的性质，因此它们携带的最初变量的信息是没有重复的，起到相互补充的作用.主成分回归在解决实际问题上是非常重要的.

【参考文献】

[1]王松桂.主成分的最优性与广义主成分估计类[J].应用概率统计，1985（01）：27-34.

[2]童恒庆.线性回归模型及计算[M].安徽教育出版社，1987.

[3]王松桂等.主成分的最优性质[J].科学通报，1984（08）：449.

[4]杨维权.多元统计分析[M].北京：高等教育出版社，1989.