基于键合图的动力稳定装置夹钳油缸的参数优化研究*

李佳奇，王立华*，严 波

(1.昆明理工大学 机电工程学院，云南 昆明 650500；2.昆明理工大学 艺术与传媒学院，云南 昆明 650500)

0 引 言

轨道动力稳定车是一种针对道床松散横向阻力不够的一种大型铁路养护设备，具有极高的工作效率。其中，动力稳定车中的核心部件为动力稳定装置，主要作用为产生水平激振力，传递下压力[1,2]。

目前，已有很多学者对动力稳定装置进行了研究。程立[3]采用了试验与定性分析结合的方式，对WD-320型动力稳定车的横向稳定性进行了分析，得出了车辆转向架心盘踞、整车偏载增加的原因，同时得出XJJ-60K型金属橡胶减振器的减振性能不稳定等因素是造成装置不稳定的主要原因。吴汶滨[4]针对WD-320动力稳定装置箱体容易底板断裂工程问题，采用有限元法分析了裂纹形成的主要原因，并且从选材以及结构两方面提出了解决问题的方法。

20世纪50年代，PAYNTER H M提出了键合图理论，根据键合图模型，可以建立规则化的状态方程[5]；刘宏飞等[6]基于双因果键合图模型的因果路径分析法，提出了一种以系统故障可隔离性为性能指标的方法，并用实验加以了验证；KAZEMI M G等[7]基于切换观测器和键合图方法相结合的故障检测方案，提出了一种基于平均观测时间方法的线性连续时间切换系统。FAN X等[8]提出了一种先导式压力调节电磁阀的建模方法，并验证了模型的正确性；NARWAL A K等[9]基于键合图理论，建立了柔性联轴器模型，求解出了激振频率的取值范围；MONTAZERI-GH M等[10]基于键合图方法，对喷气发动机动力性能和飞机的运动进行了仿真；SINGH R等[11]基于键合图理论，建立了两足Biped机器人的三维模型，然后将键合图模型转换为Simulink模型，验证了模型的正确性。

综上所述，目前对动力稳定装置的研究主要是采用有限元法，对装置局部的疲劳寿命进行分析，或者是针对装置运行过程中的横向稳定性进行分析，但是缺少对包含液压油缸在内的动力稳定装置-轨道横向耦合系统进行的研究。

由于键合图理论可以针对多能域系统进行建模，且对动力稳定装置-轨道横向耦合系统具有极强的适用性，笔者提出一种基于键合图理论、Hertz非线性接触理论以及Euler梁理论的动力稳定装置-轨道横向耦合系统的键合图模型。

1 动力稳定装置工作原理

动力稳定装置是动力稳定车中的核心组成部分，其示意图如图1所示。

图1 动力稳定装置示意图

动力稳定装置由激振器中液压马达带动主轴旋转以及主轴上偏心块旋转，经啮合齿轮驱动从动轴旋转，带动从动轴偏心块旋转，产生水平振动，并经过下压力的配合，使道砟以一种稳定的结构重新排列，以提高道床整体的横向阻力。

动力稳定装置中的走行轮具有引导稳定装置在钢轨上走行，将水平激振力及下压力传递给钢轨的作用。稳定装置中的夹钳轮主要是与走行轮共同作用夹紧钢轨，使动力稳定装置与钢轨形成一体，从而更好地传递激振力。

2 轮轨接触分析及键合图模型

考虑到轮轨间的间隙接触与冲击力，笔者采用Hertz非线性弹性力Fk[12]与粘滞阻力Fc的分段函数及布尔运算，对夹钳轮、走行轮与钢轨间间隙传动的动态特性进行研究。

一对夹钳轮与钢轨对应Hertz非线性弹性力分段函数表达式为：

(1)

轮轨相对运动接触面的粘滞阻尼力分段函数为：

(2)

采用布尔运算表述上式，可得出间隙传动状态方程为：

(3)

式中：δZn—轮轨间嵌入量；G—轮轨间接触常数；c—轮轨间阻尼系数；v—轮轨间相对速度；u1—布尔变量；u2—布尔变量；ф1—布尔变量；ф2—布尔变量。

u1、u2、ф1、ф2对应的状态为：

(4)

(5)

每个方程中若一个布尔变量为1，另一个则为0。动力稳定装置中其他夹钳轮、走行轮与钢轨的间隙传动表达式与上式类似，只是弹性力与阻尼力的正负与取值区间取决于轮轨相对位置。

3 液压油缸及其键合图模型

动力稳定装置的液压回路有卸荷保压系统，当液压回路所受压强过大时，卸荷阀将会卸掉液压回路中的压强，保持液压回路压强的恒定。

动力稳定装置液压油缸的原理为：

(6)

式中：A1—有杆腔的有效面积；A2—无杆腔的面积；Q1—为输入流量；p1—压强；Q2—输出口流量；p2—压强；Fa1—活塞输出力；Fa2—液压油缸缸体输出力；v1—活塞杆速度；v2—液压油缸缸体速度。

液压油缸的键合图模型如图2所示。

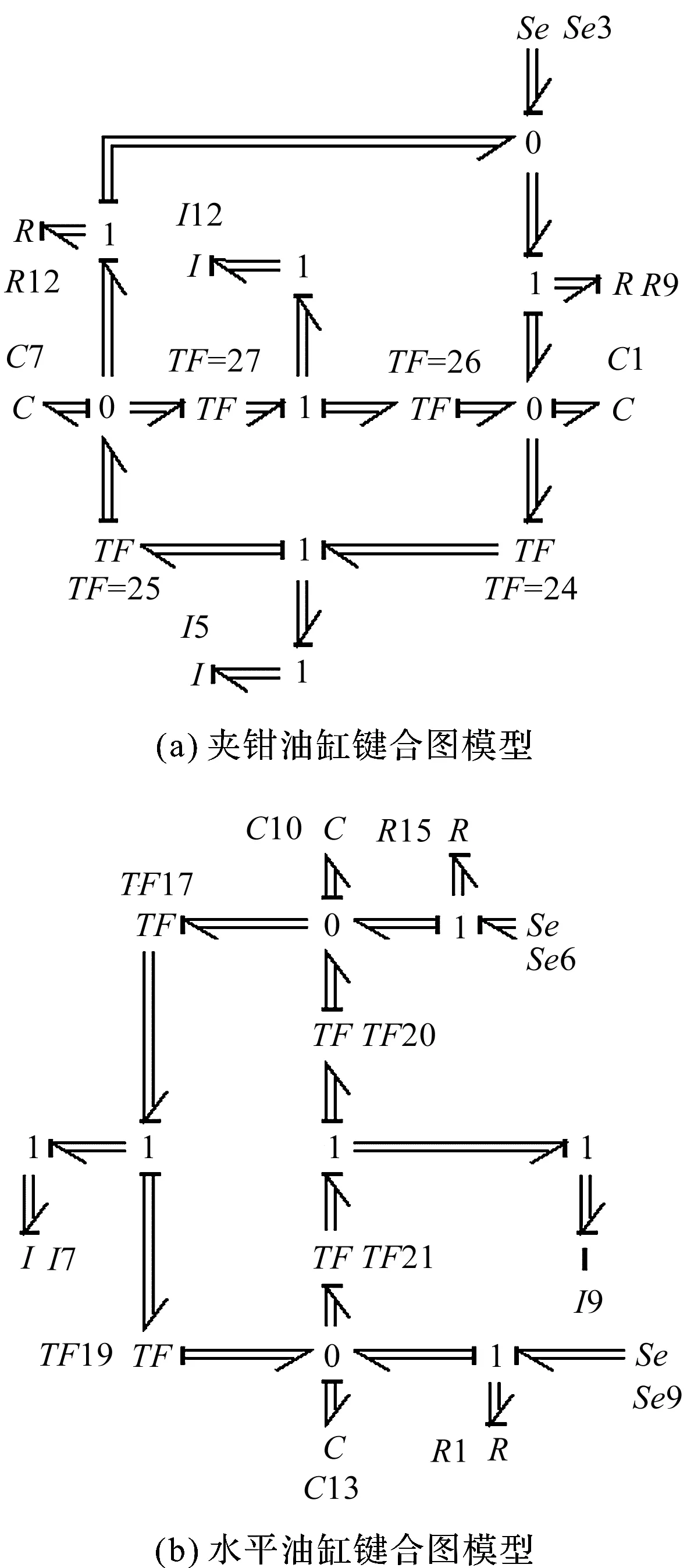
图2 液压油缸键合图模型I12—夹钳油缸缸体质量；I9—水平油缸缸体质量；I5—夹钳油缸活塞质量；I7—水平油缸活塞质量；C1—夹钳油缸无杆腔液容；C13—水平油缸无杆腔液容；C7—夹钳油缸有杆腔液容；C10—水平油缸有杆腔液容；R12—夹钳油缸出油口液阻；R9—夹钳油缸进油口液阻；R1—水平油缸进油口液阻；R15—水平油缸出油口液阻；Se9—进油口压强；Se6—出油口压强；Se3—差动连接的供油压强

图2中，动力稳定装置的夹钳油缸为差动连接，油缸的进出油压等于液压回路的压强，活塞杆因为有杆腔与无杆腔的压力差向前伸出，对轮对提供压力；水平油缸的出油口直接与油箱相连接，所以水平油缸的进油口压强等于液压回路压强，出油口压强为0 MPa。

夹钳油缸与水平油缸的键合图模型均考虑了油缸的液容效应及进出油口处的液阻效应。

4 轨道键合图模型

虽然理论上钢轨为无限长度支撑梁，但当计算长度取足够长，提取到足够的模态组数时，可以获得相对精确的结果[13]。基于Euler梁建模时，钢轨所受的力分别为走行轮、夹钳轮与走行轮对于钢轨的横向作用力，及扣件对钢轨提供的横向支撑力。

钢轨柔性化键合图理论模型如图3所示。

图3 钢轨柔性化键合图理论模型0—梁上的等势节点；TF—振型函数ф(x)；C—模态刚度ki；I—模态惯性Mi；1—广义坐标q(t)

模态刚度Ki与模态惯性Mi分别为：

(7)

式中：ωi—梁的固有频率；ρ—钢轨密度；A—钢轨的横截面积。

单根钢轨与2个动力稳定装置的6个车轮接触点的振型函数表达式为：

(8)

式中：xw0—前动力稳定装置前走行轮坐标；xc0—前动力稳定装置夹钳轮坐标；xr0—前动力稳定装置后走行轮坐标；xw1—后动力稳定装置前走行轮坐标；xc1—后动力稳定装置夹钳轮坐标；xr1—后动力稳定装置前后行轮坐标；v—动力稳定装置的走行速度；l—钢轨长度。

5 整体键合图模型

为确保结论准确可靠，笔者选取100 m长钢轨，167根轨枕，及钢轨的前100阶模态用于计算。

动力稳定装置-轨道横向耦合系统键合图模型如图4所示。

图4 动力稳定装置-轨道横向耦合系统键合图模型Se5—激振源；I13—动力稳定装置质量；TF13—左端走行轮在钢轨上振型函数；TF14—右端走行轮在钢轨上振型函数；TF2—左端夹钳轮在钢轨上振型函数；TF4—右端夹钳轮在钢轨上振型函数；TF1—右端扣件在钢轨上振型函数；TF3—左端扣件所对应钢轨位置的振型函数；Lpr—左端夹钳轮与钢轨间的弹性力；Rpr—右端夹钳轮与钢轨间的弹性力；R5右端夹钳轮与钢轨间的阻尼力；R3—左端夹钳轮与钢轨间的阻尼力；C—右端扣件的刚度；C5—左端扣件的刚度；R—右端扣件的阻尼；R4—左端扣件的阻尼；C2—轨枕道砟间的弹性力；R1—轨枕道砟间的阻尼力；I3—轨枕质量；TF6—右端轮轨接触力与动力稳定装置转矩的比例关系；TF11—左端轮轨接触力与动力稳定装置转矩的比例关系；TF8—前激振力与动力稳定装置转矩的比例关系；TF9—后激振力与动力稳定装置转矩的比例关系；Se1—前激振力；Se2—后激振力；I4—动力稳定装置的转动惯量；I5—左端前夹钳轮质量；I6—左端后夹钳轮质量；I11—右端前夹钳轮质量；I17—右端后夹钳轮质量；I6—动力稳定装置车轮质量；C6，C3—钢轨左端与右端的模态刚度；I12，I1—钢轨左端与右端的模态惯性；Area A—动力稳定装置的左端夹钳油缸键合图模型；Area B—右端夹钳油缸键合图模型；Area C—水平油缸键合图模型

笔者建立了完整的动力稳定装置轨道耦合模型，共包括2个动力稳定装置，考虑了动力稳定装置走行、横向振动与摆头转动3个自由度；将道床与轨枕间的接触简化为弹簧阻尼系统；同时也考虑了液压油缸的双向支撑作用。

6 仿真结果与实验结果对比

6.1 动力稳定车试验

为了验证键合图模型的准确性，笔者进行了轨道动力稳定车现场实车实验，装置现场实验图如图5所示。

图5 动力稳定装置现场实验图

笔者在动力稳定装置与轨枕上分别安装了加速度传感器，以便提取动力稳定装置与轨枕的横向加速度。

6.2 理论模型验证

为验证仿真结果的准确性，笔者将激振频率为35 Hz下动力稳定装置与轨枕横向加速度的实验结果与仿真结果进行对比。

动力稳定装置-轨道横向耦合系统具体的参数如表1所示。

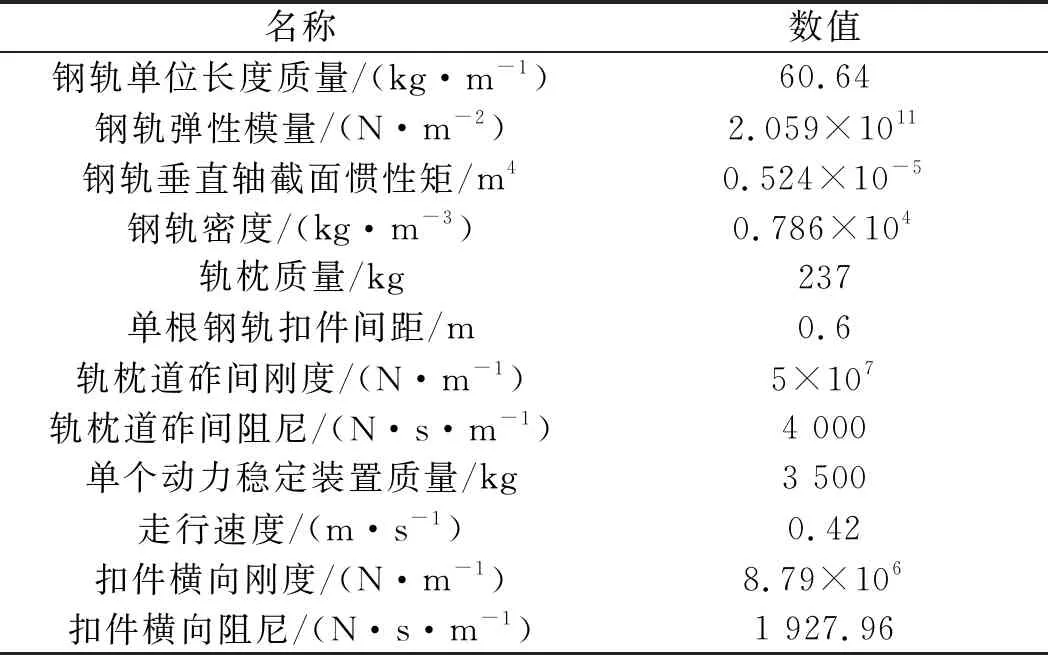
表1 动力稳定装置-轨道横向耦合系统参数

实验与仿真响应结果的对比图如图6所示。

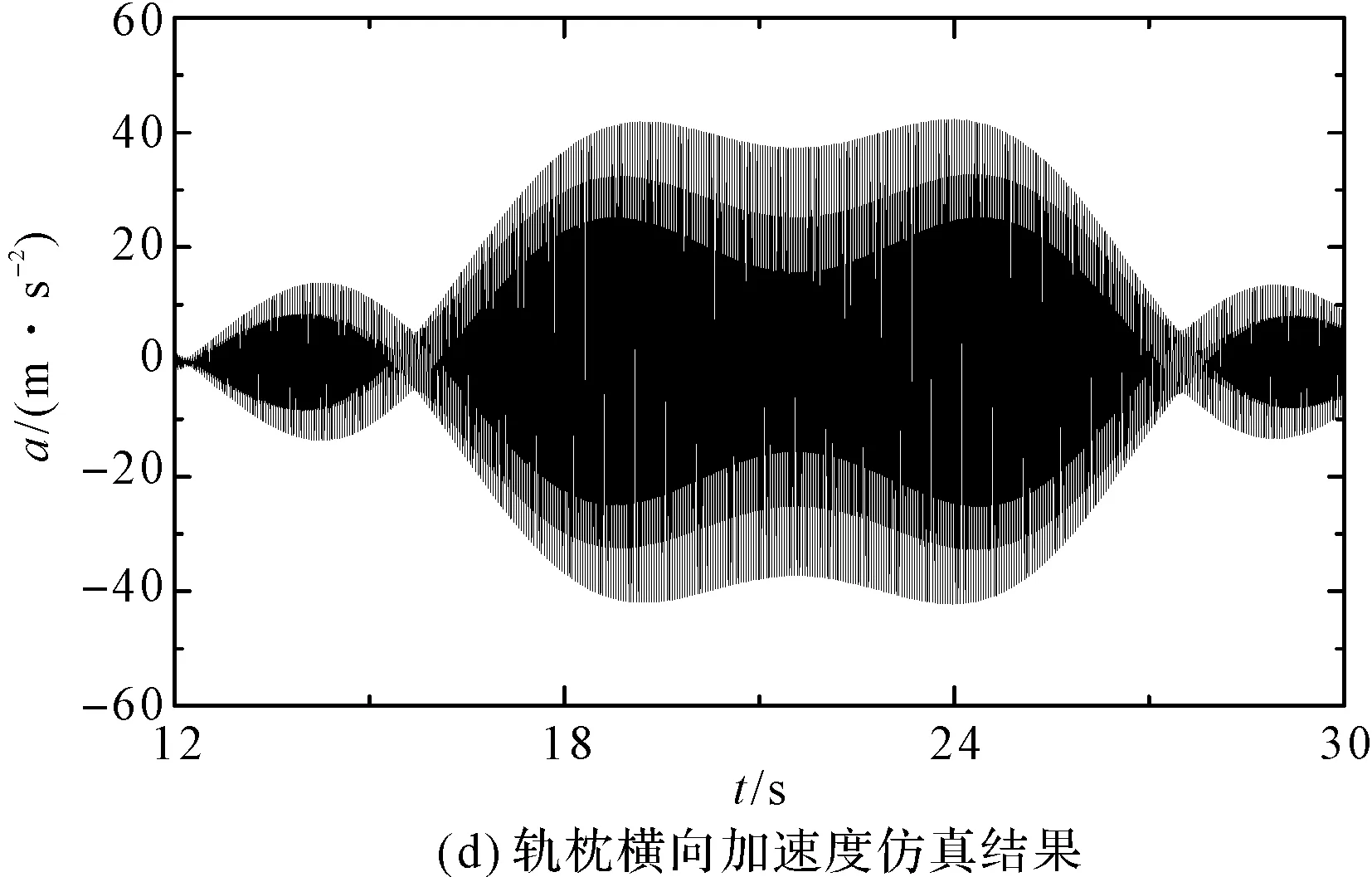
图6 实验与仿真响应结果的对比图

从图6中可知，动力稳定装置的横向加速度在50 m/s2上下波动，横向加速度稳定在53 m/s2；从对比结果可知，仿真结果与实验结果幅值较为贴近，并且趋势相同，很好地反映了动力稳定装置的横向振动特性；

从图6中还可知，轨枕的仿真结果与实验结果幅值较为贴近，并且趋势相同，反映了2个动力稳定装置从轨枕上方经过时轨枕加速度的动态特征；随着第1个动力稳定装置靠近加速度幅值逐渐增大，第1个动力稳定装置远离后加速度幅值逐渐减小，到第2个动力稳定装置靠近远离重复上面结果。

7 基于整体键合图模型的仿真分析

在传递激振力与维持轮轨的关系中，液压油缸起到了至关重要的作用。

在激振频率为30 Hz，水平油缸为6 MPa的情况下，夹钳油缸不同压强对应的轮轨间相对距离(正数为轮轨嵌入深度，负数为轮轨间隙)如图7所示。

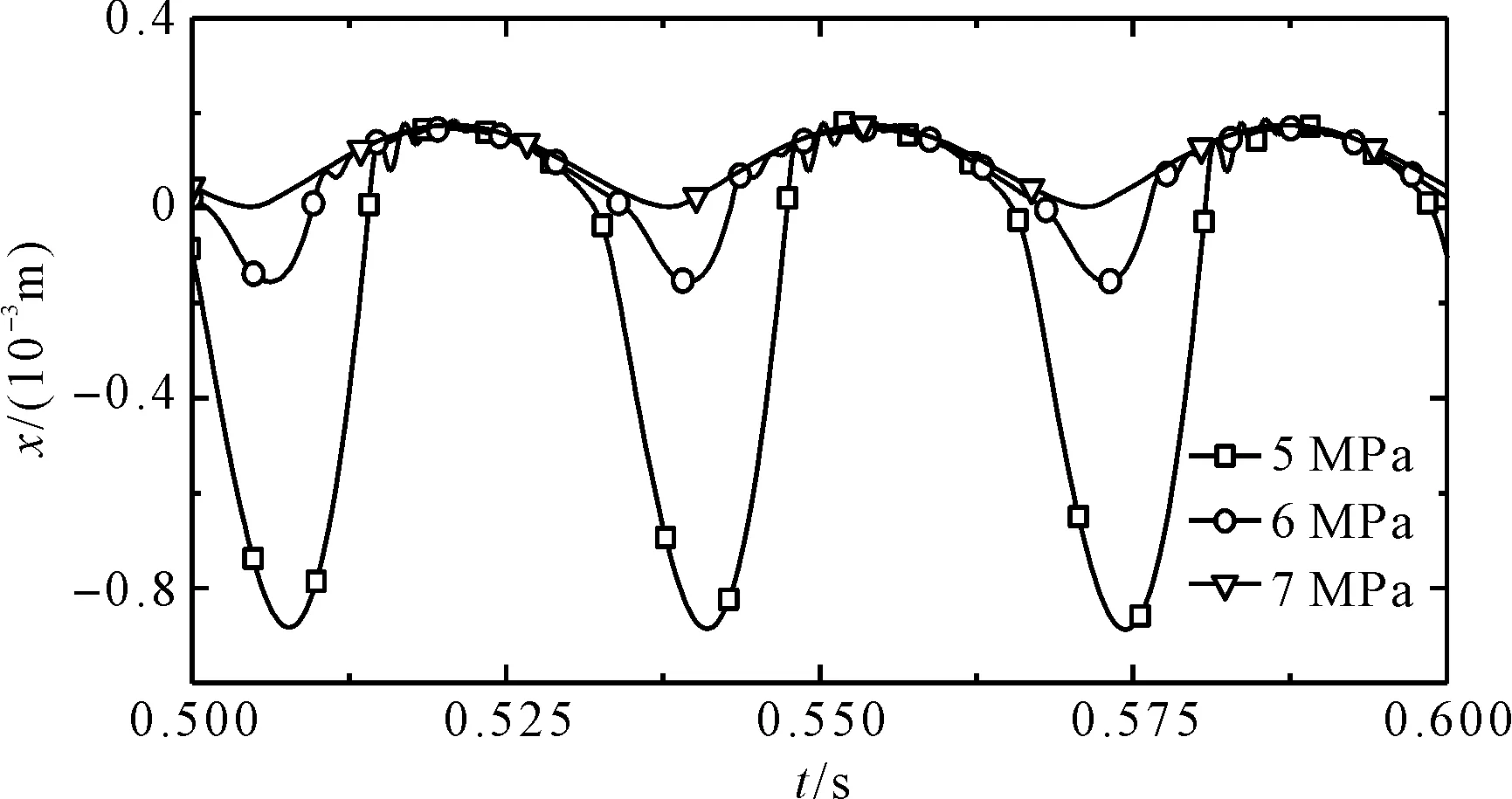
图7 不同油缸压强下的轮轨相对距离

图7中，当动力稳定装置夹钳油缸工作压强为5 MPa时，夹钳轮与钢轨间产生0.000 9 m左右的较大间隙；当达到夹钳油缸的工作压强为7 MPa时，轮轨间隙为0 m。由此可见，在此情况下可以维持相对稳定的轮轨关系。

笔者在20-Sim仿真软件中，对夹钳油缸的压强进行参数扫描，得到不同压强下的轮轨间能量传递效率。

不同油缸压强下的轮轨能量传递效率如图8所示。

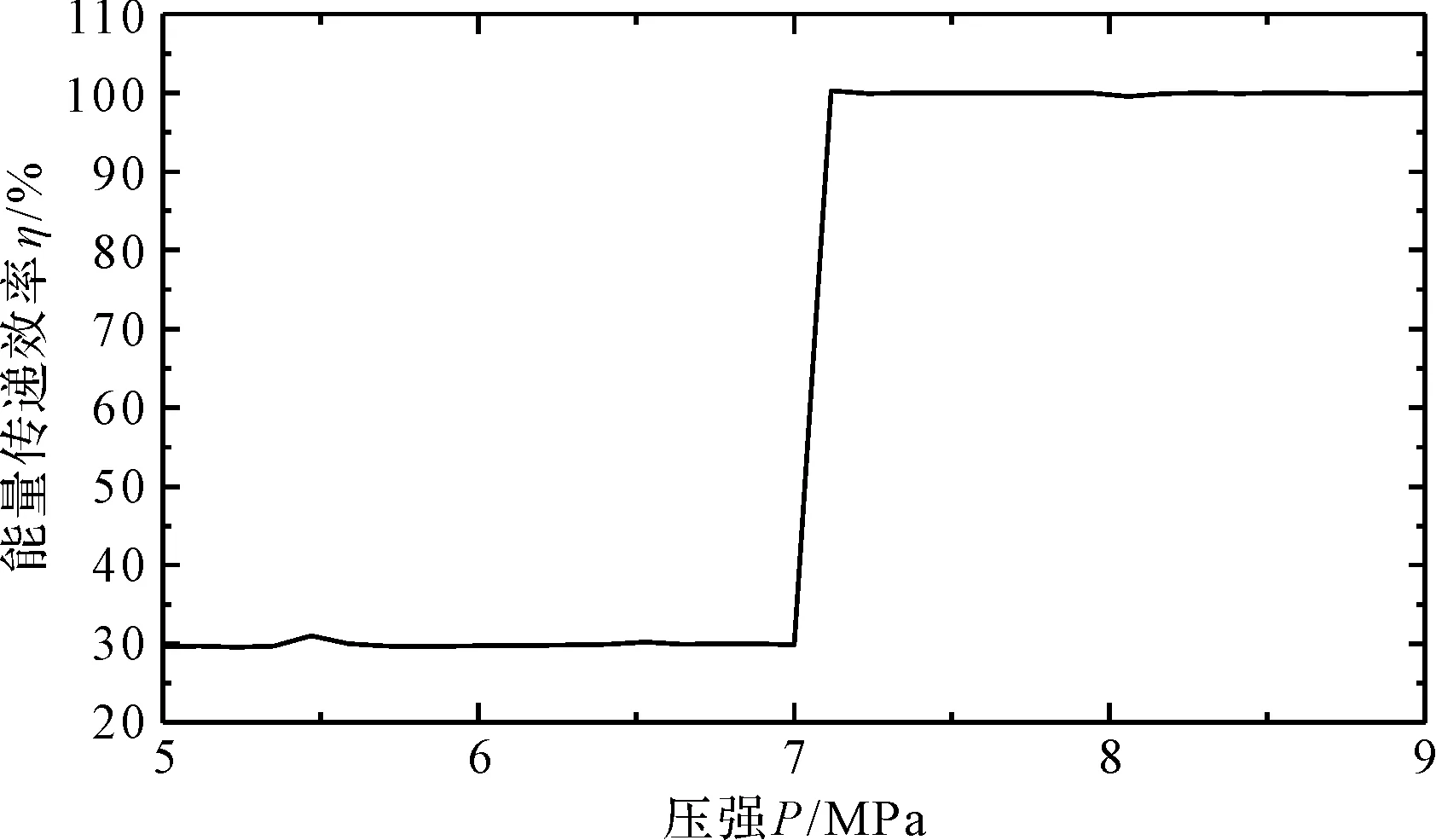
图8 不同油缸压强下的轮轨能量传递效率

图8中，在轮轨间隙消除时(夹钳油缸工作压强为7 MPa)轮轨间能量传递效率会从30%激增到99%左右，提升了66%。这是由于当轮轨间隙消除时，不存在轮轨间的冲击力，因此阻尼力对能量的消耗急剧减少，从而较大程度地提升了轮轨间能量的传递效率。

同样的，在20-Sim仿真软件中，对激振频率30 Hz，夹钳油缸为10 MPa，水平油缸为6 MPa时的夹钳油缸的进出油口的液阻参数进行参数扫描，得到不同液阻参数下的轨枕单位时间内位移的绝对值之和。

不同液阻系数对应的轨枕总位移如图9所示。

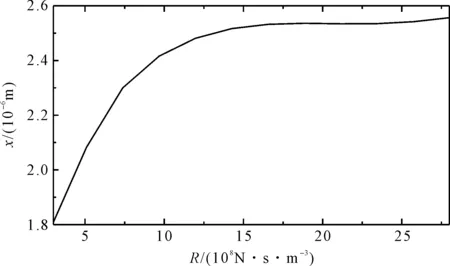
图9 不同液阻系数对应的轨枕总位移

从图9中可以看出，进油口出油口处的液阻也会对作业效果产生很大的影响；随着液阻系数的不断增大，动力稳定装置的作业效果变得明显，且当液阻参数达到1.2×109N·s/m5后趋于稳定。

8 结束语

为准确地模拟动力稳定装置实际作业的动态特性，笔者分别针对轮轨间Hertz非线性接触特性、轮轨间间隙传动、油缸的结构特性等进行了分析；结合Euler梁理论建立了动力稳定装置-轨道横向耦合模型，并根据对上述模型的分析得出以下结论：

(1)当激振频率恒定时，如果夹紧液压缸的压力增加，则轮轨关系将变得更紧密，从而可以提高能量的传递效率；在激振频率为30 Hz时，至少需要7 MPa的压强才能维持稳定的轮轨关系；当轮轨间隙消失时，轮轨间能量传递效率会激增66%；

(2)随着夹钳油缸的进出油口液阻系数的增加，可以明显改善动力稳定装置的工作效果；液阻参数至少要求1.2×109N·s/m5，才能保证工作效果。