基于RBF神经网络的电磁轴承基础激励主动控制研究*

赵宏凯，蒋科坚

(浙江理工大学 信息学院，浙江 杭州 310018)

0 引 言

主动电磁轴承(AMB)也可称为电磁轴承，是一种新型的转子悬浮支承技术。与滚动轴承和滑膜轴承相比，电磁轴承不但可以无接触地支承转子，还可以有效避免传统机械轴承耗损大、不耐磨、能效低等问题。在某些高性能要求环境下，例如高转速机械等领域有着广泛的应用，电磁轴承还可以通过控制策略实现对支承特性的有效调节，达到对电磁轴承转子系统的主动控制。

电磁轴承的动力学建模是研究电磁轴承的前提之一，其控制方法的优良和控制器设计的好坏是决定电磁轴承系统旋转精度、动态性能和稳定性能的关键。

目前，学者们在电磁轴承动力学建模和控制算法的研究上，已取得了不少成果。田拥胜等[1]针对一台4 000 r/min、50 kW的高转速电磁轴承转子系统进行了承载力建模，并对其刚度阻尼和系统性能进行了分析，给出了高转速下电磁轴承的运行规律；SUN Z等[2]提出了一种单元映射的全局分析方法，在获取电磁轴承全局结构的同时，研究了各参数对性能的影响。胡永等[3]将电磁轴承的动力学内容与传统机械轴承进行了对比，并在磁力轴承API617标准下进行了动力特征分析，得出了两者的不同之处；莫逆等[4]通过有限元方法，计算了转子在外扰力作用下的传递频率响应、位移响应及动态力响应，并与滚珠轴承进行了对比，考察了电磁轴承的振动传递特性；LYU M等[5]在电磁轴承系统响应识别的基础上，提出了一种阻尼系数整定PID控制方法，有效地抑制了转子振动；YUAN Y等[6]选取控制电流和目标平衡位置，在不涉及任何模型信息的基础上，提出了一种三自由度电磁轴承无模型自适应控制方法，简化了模型分析过程；蒋科坚等[7]提出了一种基于基础加速度信号为参考信号，包含自适应滤波器的电磁轴承-刚性转子系统的基础激励响应抑制方法，有效抑制了基础激励造成的转子振动响应，但基础激励仅为平稳振动时才有效。

随着现代控制技术的发展，神经网络智能控制方法被广泛应用于高精度、高效率的控制器设计中，有效提高了系统的控制性能。KUMAR P等[8]针对未知非线性SISO非仿射系统，基于Lyapunov稳定性理论，提出了一种RBF网络估计等效仿射非线性系统的控制方法；罗隆等[9]提出了一种渐近稳定的自适应神经控制方法，在连续的自适应鲁棒控制项中，实现了闭环系统的渐近跟踪，减轻了控制输入的颤振问题；SUN Y G等[10]在磁悬浮非线性仿射的数学模型上，设计了一种基于RBF神经网络的滑模控制器，并采用最小参数学习法代替网络的权重，证明了控制方法的有界性和收敛性。

在电磁轴承系统的动力学分析中，虽然有大量的研究成果，但在建模过程中，通常假设转子系统安装在静止载体的基础上。然而，在实际应用当中，电磁轴承转子系统往往安装在移动载体上，此时转子系统必然会受到来自外部基础激励的干扰，引起电磁轴承转子的振动响应。因此，在静止基础上得到的动力学模型，难以满足移动载体上的电磁轴承控制设计要求。

笔者在考虑移动载体下电磁轴承的动态变化基础上，对电磁轴承转子系统进行受力分析，提出一种基于RBF神经网络的PID控制算法，来对由系统引起的振动响应进行抑制；在移动载体上电磁轴动力学模型的基础上，通过RBF神经网络实时调节PID控制参数，实现在非随机和随机基础激励下电磁轴承转子系统的稳定悬浮。

1 基础激励下电磁轴承系统动力学建模

笔者对电磁轴承支承特性的研究，沿用了传统机械轴承-转子系统等效刚度和等效阻尼的分析方法。对于电磁轴承控制系统，其支承特性总可以用支承的等效刚度和等效阻尼来表示。在线性范围内，由于单自由度电磁轴承模型能够较好地反映基础激励下系统的主要性能，笔者将电磁轴承的电磁力等效为一个单自由度的质量-弹簧-阻尼系统。

在忽略转子陀螺效应的前提下，笔者建立了基础激励下的单自由度电磁轴承支承系统，如图1所示。

图1 基础激励下的电磁轴承支承系统

在基础激励下，根据牛顿定理，笔者建立数学模型表达式如下：

(1)

(2)

式中：mr—转子质量；ms—定子质量；Ks—等效弹簧刚度系数；Cs—等效弹簧阻尼系数；Kt—定子刚度系数；U—外加控制力。

(3)

结合式(1,2)，可得基础激励下电磁轴承系统的空间状态变量表达式为：

(4)

由式(4)可得状态方程的系统矩阵A和输入矩阵B为：

(5)

(6)

(7)

计算可得电磁轴承系统的输出向量表达式为：

(8)

由式(8)可得状态方程的输出矩阵C和直接传递矩阵D为：

(9)

(10)

为观测移动载体上单自由度电磁轴承转子控制系统构造的基本特性，需要结合式(5,6)和式(9，10)进行系统能控性和能观性的判定。

根据状态能控和能观的判定定理[11]，当Ks≠Kt≠0，且mrms不为0情况下，可得：

rank(Γc[A,B])=rank([BABA2BA3B])=4

(11)

由式(11)可知，系统能控性矩阵的秩等于4，与系统的阶数相等，即电磁轴承转子系统是能控的。这意味着当定子上的转子稍稍偏离平衡位置时，总可以通过在定子-转子间施加一个适当的外力，使得将转子稳定在平衡位置，即：

(12)

由式(12)可知，系统能观性矩阵的列向量秩为4，为列满秩，即电磁轴承转子系统是能观的。这意味着，可以通过观测其转子的位移信号来确定系统中转子的速度、定子的位移量和速度等信息。

由于移动载体上电磁轴承转子系统具有可控性和可观性，则必定可以设计状态反馈控制器，来使系统保持稳定。

2 基础激励模型

在移动载体上运行时，电磁轴承所受到的基础激励有多种形式，例如随机激励和非随机激励、确定激励和非确定激励、周期激励和非周期激励等。载体以及外部环境对基础激励的大小及变化影响很大。

笔者以车辆作为移动载体，研究分析随机和非随机基础激励下的电磁轴承支承特性。其中，非随机激励选取正弦信号和方波信号；在随机激励选取上，由于得到完整全面的路面轮廓数据的难度很大。为方便实验分析，采用高斯白噪声通过一个积分器来产生随机路面不平度时间轮廓的方法。

在垂直方向上的移动载体外部激励输入模型的表达式为：

(13)

式中：f0—下截止频率，Hz；G0—路面不平度系数，m3/cycle；v0—前进速度，m/s；ω—数字期望为零的高斯白噪声。

车辆载体在行进过程中，由于存在前后轮轴距，后轮与前轮之间的外部基础激励在时间上存在一定的偏差。为方便仿真分析，此处忽略后车轮相对于前车轮的基础激励产生的时滞，将其视为同一个外部激励。

电磁轴承的非随机和随机基础激励曲线如图2所示。

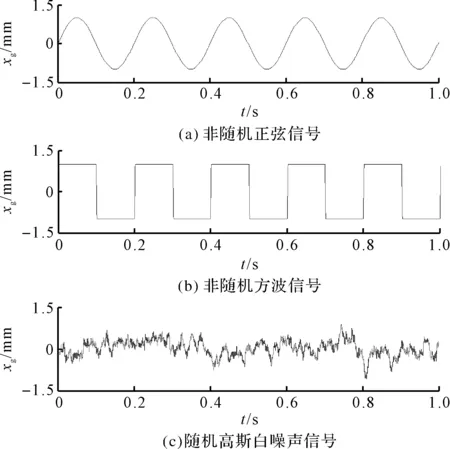
图2 非随机和随机基础激励曲线

由图2可知：在非随机信号选择上，采用频率为5 Hz，幅值为1的正弦信号和占空比为50%，频率为5 Hz的方波信号；在随机信号选择上，选取G0=16×10-6，v0=60 km/h，采样时间为0.05 s，仿真时间为1 s的随机高斯白噪声信号。

3 基于RBF神经网络的PID控制器

3.1 RBF神经网络

RBF神经网络通常分为3层，依次为输入层、隐含层和输出层。相较于BP神经网络[12]，在映射过程中RFB不会陷入局部最小，有较好的拟合效果。

RBF神经网络结构如图3所示。

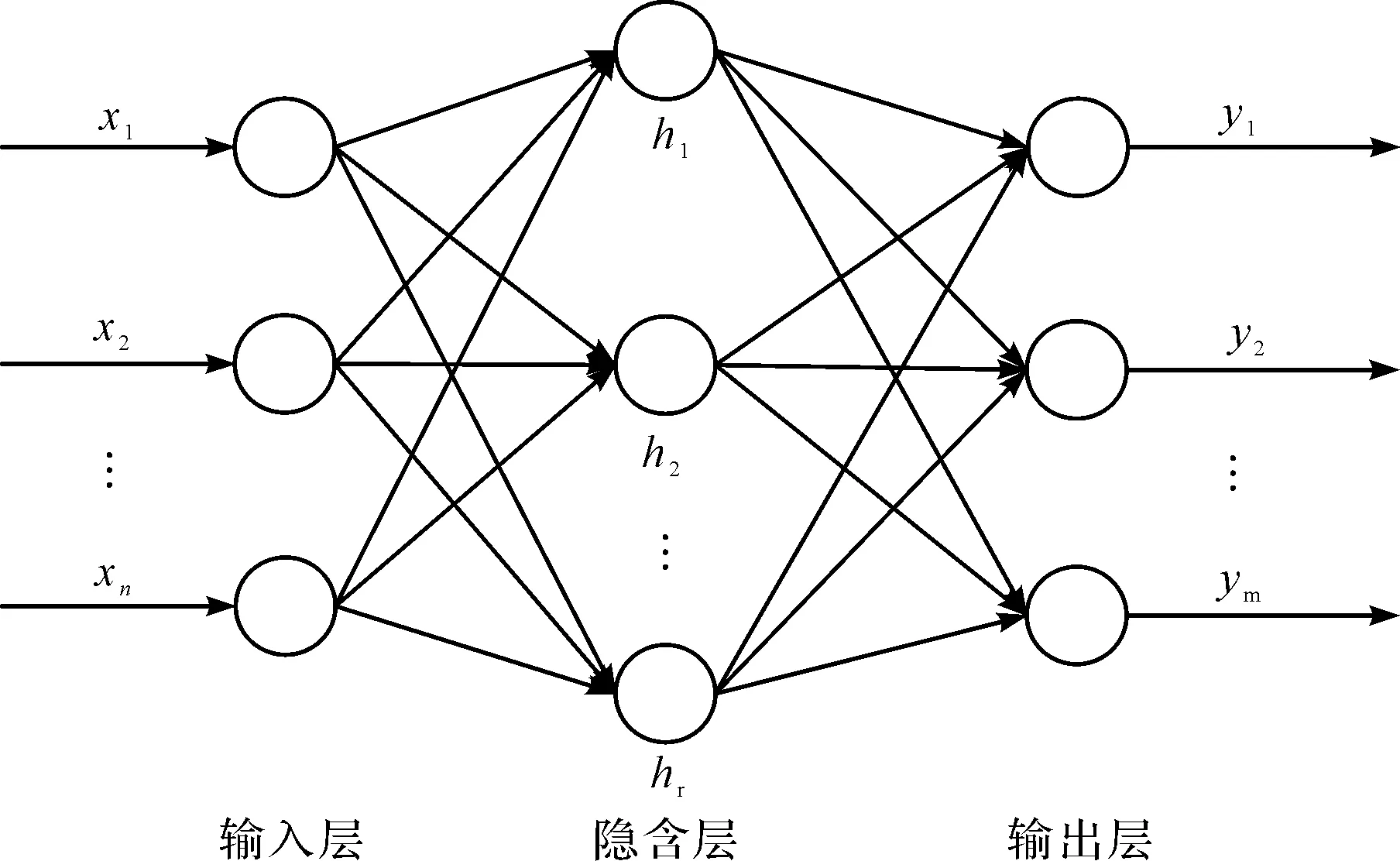
图3 RBF神经网络结构模型

RBF神经网络的隐含层采用径向基高斯函数作为激活函数，通过对各个输入数据相乘相加的计算，来实现输入向量的非线性变换，通过隐含层的多个神经元实现对任意函数的逼近。

隐含层中所用的激活函数的表达式为：

(14)

式中：cj—第j个隐含层节点的中心径向基矢量；bj—第j个隐含层节点的基宽系数；hj—第j个隐含层节点的输出向量。

RBF神经网络的输入与输出之间的关系可表示为：

(15)

式中：wij—第i个输入层节点与第j个隐含层节点之间的权重系数；uj—第j个输出层节点的输入量；ym—第m个输出层节点的输出量。

具体的迭代计算过程如下：

(16)

结合式(14，15)可得被控对象的输出与控制输入的比值，即Jacobian辨识信息矩阵为：

(17)

3.2 RBF神经网络控制器

在电磁轴承转子系统的模型基础上，笔者采用RBF神经网络控制PID的原理如图4所示。

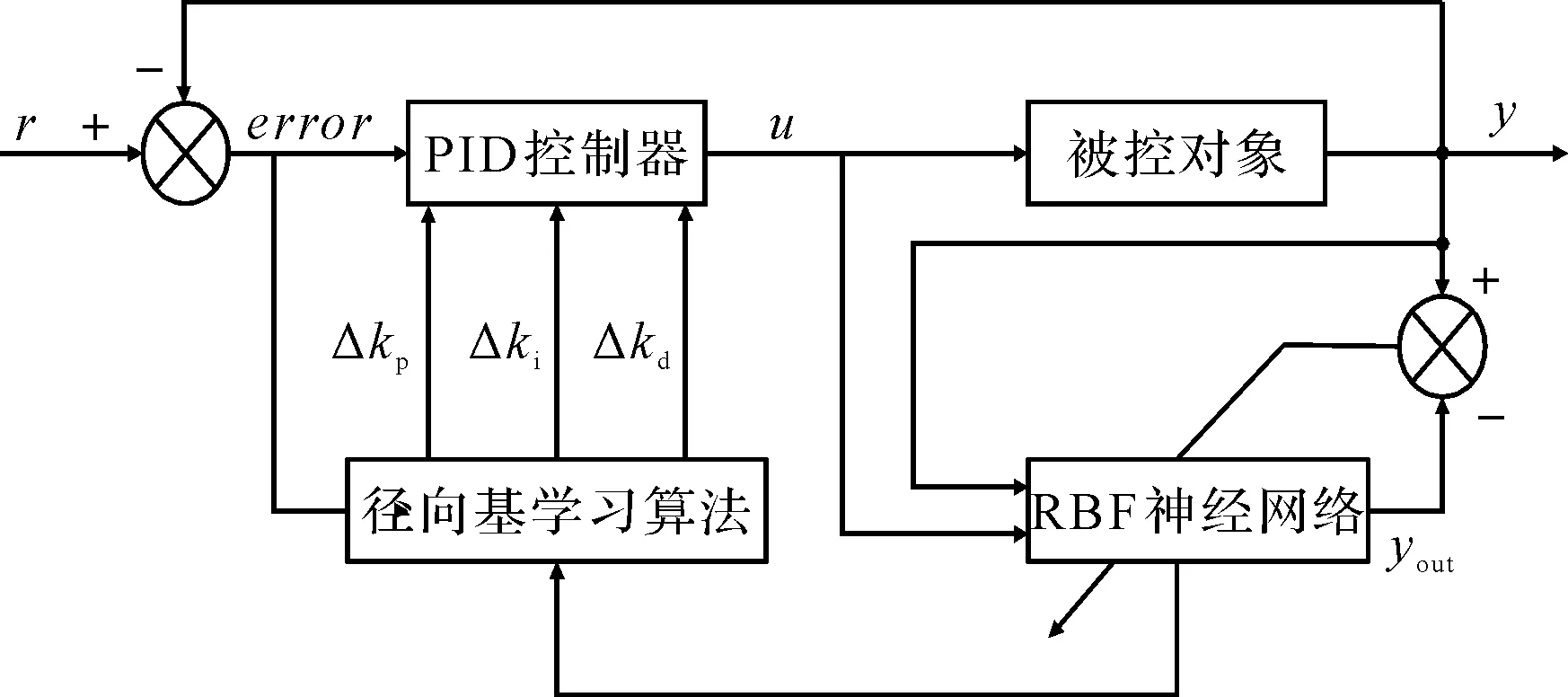
图4 RBF神经网络控制原理

笔者首先设计PID控制器，以降低转子竖直方向上的加速度为控制目标，将转子加速度的真实值和期望值之间的差值输入至PID控制器当中；在外部激励的干扰下，PID控制算法的参数不可动态调节。

笔者将PID控制方法与RBF神经网络相结合，利用RBF神经网络实现对PID参数的实时整定，以满足移动载体下电磁轴承转子系统的稳定控制。

控制偏差为e(k)下的RBF神经网络PID控制器的算法为：

Δu(k)=kp(e(k)-e(k-1))+kie(k)+kd(e(k)-2e(k-1)+e(k-2))

(18)

具体计算过程如下：

(19)

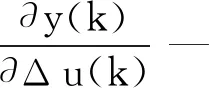
其中：x1=e(k)-e(k-1)；x2=e(k)；x3=e(k)-2e(k-1)+e(k-2)。

4 仿真及结果分析

利用MATLAB，笔者对移动载体上电磁轴承的基础激励控制系统进行仿真实验。

电磁轴承的基本参数如表1所示。

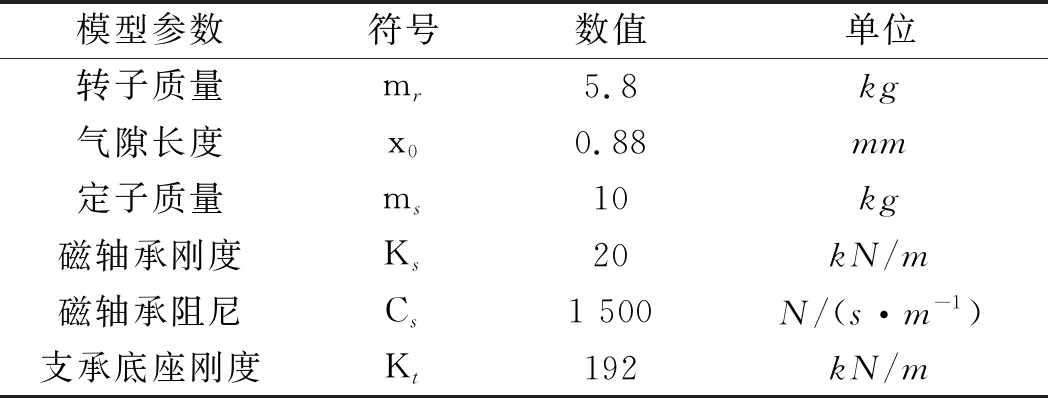
表1 电磁轴承的基本参数

根据移动载体上的电磁轴承支承模型和PID控制器模型，笔者采用基于RBF神经网络的参数自整定控制方法进行仿真。

其中，RBF神经网络的结构为3-6-1，学习速率为0.5，动量因子为0.05，初始PID控制参数为kp=0.01、ki=0.01、kd=0.01，仿真可得非随机输入信号为正弦信号的控制响应曲线，如图5所示。

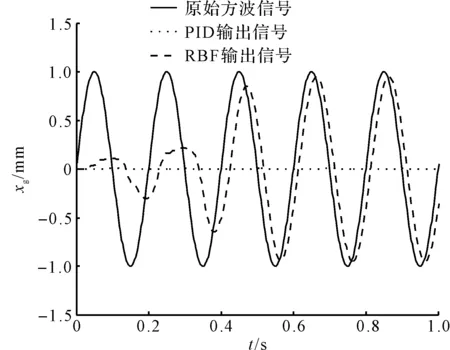
图5 正弦信号控制响应曲线

从图5中可见：由于PID控制算法的参数固定，不能随着输入波形进行实时调参，单单采用PID控制方法，在未调参的情况下，控制效果非常不理想。

RBF神经网络通过对PID参数的实时调整，在正弦信号的第3个周期，输出信号就可基本跟随输入信号，明显提高了系统的输出跟踪能力。

非随机正弦信号的控制参数调节曲线如图6所示。

图6 正弦信号控制参数调节曲线

从图6中可知：在控制初期，比例系数、积分系数和微分系数的变化波动较为明显；在0.5 s后，控制参数不再变化，达到稳定状态。

在相同条件下，仿真可得非随机输入信号为方波信号的控制响应曲线，如图7所示。

图7 方波信号控制响应曲线

在非随机方波信号下，笔者采用RBF神经网络，同样实现了控制参数的实时调整，在不进行人为参数调整的情况下，及时遵循输入信号的动态过程，输出信号在第2个周期就可基本跟随输入信号。

控制参数调节曲线如图8所示。

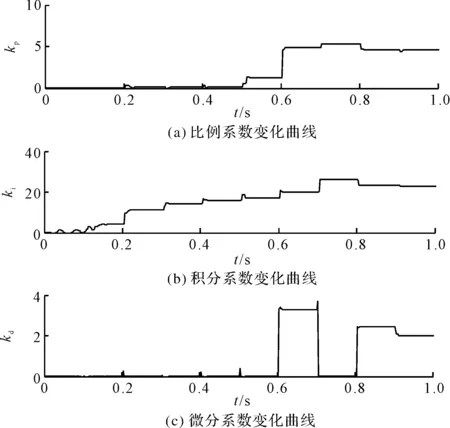
图8 控制参数自适应调节曲线

由图8可见，控制参数在方波信号下的调节呈现阶梯状，控制初期的参数变化较为平缓，在0.5 s后，比例系数和微分系数产生较大变化，并最终可得非随机方波信号的比例系数、积分系数和微分系数分别为4.5、24和2。

根据电磁轴承在移动载体上的支承模型与RBF神经网络控制模型，笔者将控制力U和随机基础激励信号xg作为输入变量，以降低最能反应转子悬浮性能的转子加速度为控制目标，通过MATLAB建模仿真，得到了移动载体下电磁轴承的转子加速度、转子动位移和定子动位移的振动响应，如图9所示。

从图9可以发现：采用RBF神经网络控制方法比采用单一PID控制方法有着更小的动态范围，控制性能也有较大地提高；

在电磁轴承转子系统的转子加速度、转子和定子动位移指标上，对于随机基础激励的振动抑制效果明显。

电磁轴承转子控制性能的均方根值如表2所示。

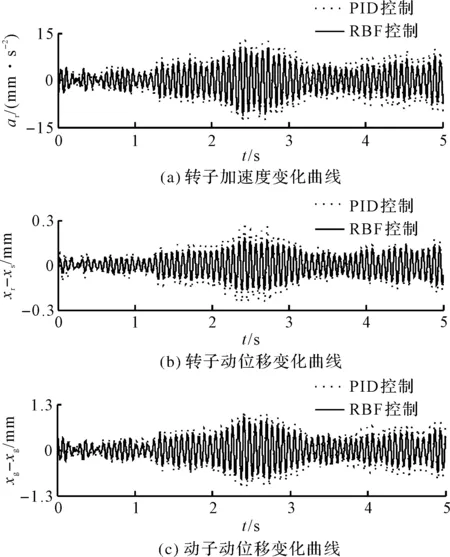
图9 随机激励下的振动响应曲线

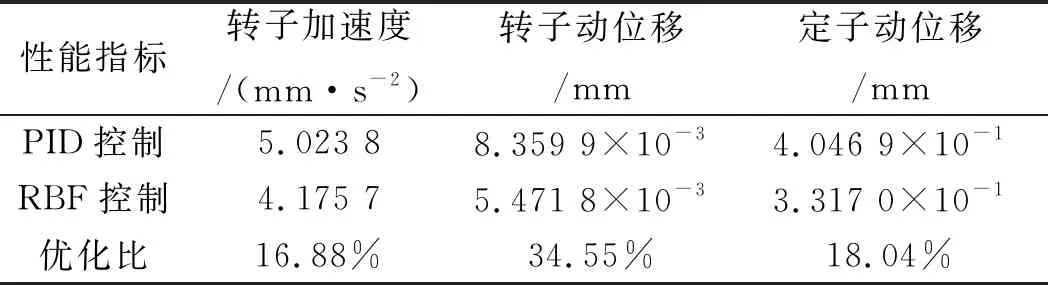
表2 电磁轴承转子控制性能的均方根值

由表2可得：在随机基础激励下，相比于PID控制方法，采用RBF神经网络控制方法在转子加速度、转子动位移和定子动位移的优化比分别为16.88%、34.55%、18.04%，有效改善了电磁轴承系统的动态变化，提高转子的悬浮稳定性。

笔者对移动载体上电磁轴承转子系统进行功率谱分析，可得到随机激励下的转子加速度、转子动位移和定子动位移的功率谱幅值曲线，如图10所示。

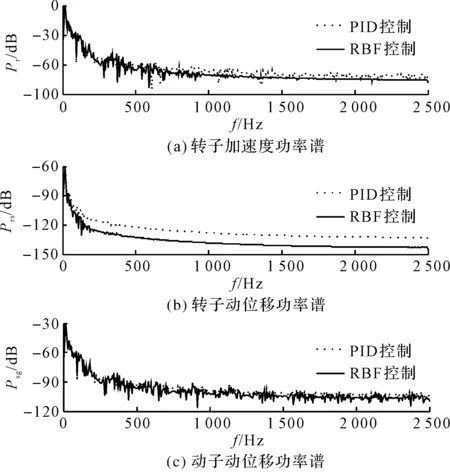
图10 随机激励下的功率谱

图10中，对比两种控制方法下的功率谱曲线可以看出：

(1)在移动载体上，相比于采用PID控制方法，电磁轴承转子系统采用RBF神经网络方法得到的幅值更低，说明该方法可以有效减小电磁轴承随机基础激励的振动；

(2)进一步观察可以发现，随机基础激励对电磁轴承转子系统的振动集中在低频部分，随着频率的增大，振动幅值逐渐降低，可见在基础激励下的电磁轴承转子系统的控制研究上，应当关注低频部分对其产生的影响。

5 结束语

笔者通过建立移动载体上的单自由度电磁轴承支承模型，研究了在非随机基础激励和随机基础激励下，采用RBF神经网络控制方法的情况下，电磁轴承系统的转子加速度、转子动位移和定子动位移的变化趋势，通过仿真分析，可得到如下结论：

(1)移动载体上的单自由度电磁轴承系统的空间状态模型具有可控性和可观性；

(2)在周期正弦信号和方波信号下，RBF神经网络控制方法可以有效提高系统的控制性能，可自适应调节PID参数，使系统输出紧紧跟随期望输入；

(3)在随机高斯白噪声信号下，RBF神经网络控制方法对转子的加速度、转子动位移和定子动位移改善明显，性能分别提升了16.88%、34.55%和18.04%，使电磁轴承转子系统在随机基础激励下实现稳定悬浮；

(4)移动载体上的电磁轴承转子系统的振幅最大值出现在频率较小处，低频基础激励对电磁轴承系统的振动影响较大。