基于内阻估计燃料电池热功率的建模与分析

魏永琪，赵玉兰，贠海涛

（青岛理工大学机械与汽车工程学院，山东青岛 266520）

质子交换膜燃料电池（proton exchange membrane fuel cell）因其环保、启动快、运行温度低、高效、不存在卡诺循环限制等优点，已成为世界各国推动汽车研究迈向新时代的重要研究对象之一［1-2］。质子交换膜燃料电池系统是多输入、多输出的系统［3］，与主要参数之间相互耦合不易单一控制。考虑到系统的复杂性，设计更为可靠的质子交换膜燃料电池管理系统对其在汽车领域的商业化具有重要意义。

质子交换膜燃料电池热功率是燃料电池系统在运行过程中的重要产物之一。燃料电池自身的散热处理能力不仅关乎燃料电池运行的稳定性，也关乎燃料电池的寿命。实现燃料电池运行过程中的温度可控，将燃料电池的温度稳定在合理范围内是本研究的核心。

目前，燃料电池自身热功率的研究已取得一定进展。李菁等［4］从燃料电池汽车的散热角度出发，设计了针对全功率燃料电池的汽车散热系统，研究对象不仅包括燃料电池，同时包含了DC/DC、空压机和负载电机的散热处理器件，利用 GTCOOL软件模拟燃料电池汽车的散热系统，并与实际数据对比证明模型的准确性。张宝斌等［5］从燃料电池自身的散热角度出发，论述了目前针对燃料电池散热的诸多控制策略和冷却方法。展茂胜［6］从质子交换膜燃料电池热功率数学模型出发，基于冷却循环的控制策略，对燃料电池的冷却子系统进行相应的优化研究。上述关于质子交换膜燃料电池的产热和散热研究［7-9］中，主要是从燃料电池的产热功率计算开始，基于此热功率值进行散热系统或散热控制策略的研究，所建立的燃料电池热模型并不能更深入地反映燃料电池的内部运行情况。同样，热模型也缺少一些燃料电池内部情况的真实显现。

本研究中，建立以内阻估计为基础的针对燃料电池热功率计算的数学模型。燃料电池内阻并不是一个真实存在的物理值，而是建立在燃料电池等效输出模型基础之上估算的等效内阻。等效内阻即燃料电池自身极化损失的数值化和具体化。极化损失为供给至燃料电池内部的反应物蕴含的化学能，并未完全转化成相应的电能（剩余部分转化成热能）。燃料电池自身的热能不仅包括此部分还包括在燃料电池内部完成物质传输（电子移动、质子移动等）时所产生的热量。因此，建立基于等效内阻的燃料电池热功率模型，以实现对燃料电池运行过程的进一步描述。

1 质子交换膜燃料电池结构及模型

1.1 燃料电池内阻分析

对燃料电池内阻进行分析前，先对燃料电池的极化曲线进行描述。本实验中，燃料电池单体的极化曲线见图1。

从图1可以看出，燃料电池单体电压随着输出电流密度的增加经历了3部分区域。这3部分区域分别为活化极化区域、欧姆极化区域和浓差极化区域。根据Kim等［10］对燃料电池电压经验模型的研究，燃料电池单体电压与输出电流密度之间的关系为：

式中：E0为理论上燃料电池单体的开路电压（V）；E为燃料电池单体的输出电压（mV）；Id为燃料电池单体的输出电流密度（A· cm-2）；A为燃料电池单体的活化面积（cm2）；b为Tafel斜率；RΩ为燃料电池单体欧姆内阻；m和n均为常数，其值分别与电压和电流密度有关。

结合以上分析和相关燃料电池的结构知识，将燃料电池内阻分为大致3种：①活化极化内阻：由燃料电池内部进行的电化学反应体系的性质决定；②欧姆极化电阻：主要包括燃料电池各单体内部的结构内阻，如双极板自身电阻、扩散层自身电阻、催化层自身电阻和质子交换膜自身电阻等，该部分电阻是燃料电池内阻的主要部分；③浓差极化电阻：主要由反应离子浓度变化造成。

为便于对上述燃料电池极化损失进行解释，同时为了进行燃料电池内阻估计，采用Randles电路模型［11］来表示燃料电池等效电路，其结构如图2所示。图2中，E为燃料电池的理论输出电压；U为燃料电池的实际输出电压；RΩ为燃料电池的欧姆等效内阻；Rp为燃料电池活化极化损失和浓差极化损失等效电阻之和；Cp为燃料电池内部双层结构的等效电容。

1.2 燃料电池内阻估计器

燃料电池内阻估计器主要由两部分组成：一部分是内阻估计器所需的算法，另一部分是基于算法的估计器数学模型。

1.2.1 卡尔曼滤波算法

卡尔曼滤波（Kalman filter）算法适用于不易直接监测参数数值的估算，同时具有可实时在线监测的优点。卡尔曼滤波的运算过程需要建立在相应的模型之上，将模型的状态方程进行离散化，通过一步预测和一步预测值优化的过程不断使估计结果越来越准确。此过程也包括对预测方差的不断优化。优化均依靠核心数据即卡尔曼增益矩阵。

卡尔曼滤波算法主要包括5个步骤。

步骤1 状态参数预测。

步骤2 状态更新。

步骤3 协方差矩阵预测。

式中：P为协方差矩阵；Г为噪声驱动矩阵；Q为白噪声矩阵。

步骤4 协方差优化。

式中：P·为协方差优化值；In为单位矩阵；H为观测矩阵。

步骤5 卡尔曼增益矩阵计算。

式中：R为白噪声矩阵，与Q不相关。

卡尔曼滤波算法作为内阻估计过程中的重要算法，实现燃料电池内阻估计还需燃料电池的等效模型。基于卡尔曼滤波算法的内阻估算模型结构见图3。

1.2.2 内阻估计数学模型

以燃料电池等效电路模型为基础，由于在燃料电池的运行过程中对各项参数的监测有相应的时间间隔，所以数据的采集是离散的。使用卡尔曼滤波算法前，首先将等效电路模型状态方程离散化：

式中：uc为等效电路中电容两端的电压；Rp为活化极化和浓差极化致使电压损失的等效电阻；Cp为双层电容，用以体现燃料电池内部表面的多孔结构电学特性；Ea为在输出电流为I的情况下燃料电池的输出电压；RΩ为燃料电池欧姆内阻；E0为燃料电池的理论输出电压；w和v分别是系统噪声和观测噪声，二者为不相关的白噪声；T0是定值，为采样时间周期。

燃料电池内阻估计的数学模型为：

式中：ucp为电容Cp端电压预测值；k为离散时间点；ucn为电容Cp端电压预测优化值。

式中：Pcp为状态的协方差预测值；Pcn为状态的协方差最优估计值；Qp为一个系统噪声方差。

在电容Cp端电压的预测过程中，卡尔曼增益为：

式中：Kc为电容Cp端电压预测过程中的卡尔曼增益；Hc为观测系数矩阵；Rc为电容Cp端电压预测过程中观测噪声的方差矩阵。

电容Cp端电压的优化预测值为：

其中，

电容Cp端电压预测过程中协方差优化矩阵为：

则燃料电池内阻为：

式中RΩ为燃料电池在输出电流为I时的内阻。

需要注意，进行燃料电池内阻估算时要做燃料电池等效电路初值的设定，燃料电池内阻初值则根据单体电压极化曲线欧姆区域斜率来获得，初始电容Cp两端电压为0。

1.3 燃料电池热模型计算

对燃料电池输出电流密度进行相应设定，即规定燃料电池的输出在欧姆区域，故此刻燃料电池内阻主要是等效欧姆内阻。此内阻估计值表示燃料电池在运行过程中极化损失的数值化，而损失的化学能并没有转化成电能，而是转化成相应的热能。基于此，燃料电池的热功率计算数学模型为：

式中：PH为燃料电池的产热功率（W）；Kst为燃料电池热模型修正系数。

在模型中，燃料电池热功率模型修正系数表明：针对电堆在实际运行过程的校正，而加入欧姆内阻估计值则是将燃料电池在运行过程中的化学能损失数值化代入到燃料电池热功率的分析过程中。

2 燃料电池系统模型及实验过程

以实际的质子交换膜燃料电池为核心，进行燃料电池内阻的估计实验和热功率计算模型的仿真实验。

2.1 PEMFC及其供给系统

实验中采用的质子交换膜燃料电池的额定输出功率为45 kW，由EK公司生产，燃料电池电堆实物图见图4。电池电堆的基本参数如表1所示。

表1 燃料电池电堆结构参数

燃料电池能产生电能是依靠与氢气（H2）、氧气（O2）的氧化还原反应，两种反应物并未直接混合，分别处于不同的反应室，产生相应电子的外部移动从而形成电流。两个反应室分别称为阴极和阳极。阳极的化学方程式为：

阴极的化学方程式为：

2.2 PEMFC冷却循环子系统

燃料电池冷却液循环子系统中核心部件之一是水泵，其功用是使冷却液获得相应的流动速度和相应的绝对压力，让冷却液在管路中流动将燃料电池内部的热量带出，维持燃料电池内部的温度平衡。实验台架中使用的水泵为EMP公司出产，其map图见图5。

2.3 实验过程设计

实验过程设计主要为燃料电池内阻的估计和燃料电池在同一工况运行条件下热模型的建立。

2.3.1 内阻估计过程

在以质子交换膜燃料电池为核心的实际实验台架上，PEMFC模拟运行的工况为FTP（federal test procedure）工况。在此模拟工况中通过对燃料电池输出电压、输出电流密度等相关参数的监测，燃料电池控制单元（FCU）运用监测数据和设计好的内阻估计器进行内阻估算。燃料电池在FTP工况模拟中的主要参数如表2所示。

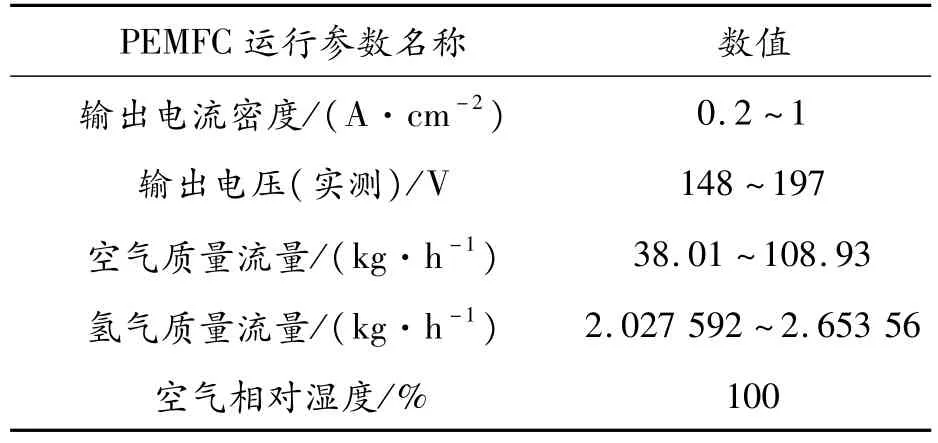
表2 燃料电池运行参数

2.3.2 热模型建立与仿真过程

在热模型建立与仿真过程中，最为重要的部分是利用燃料电池实际运行中的参数对文献［12-15］中的热模型进行校正，从而使其适用于此电堆。其次，将此校正热模型计算的热功率与实验中的热模型进行对比，验证基于内阻热模型建立的可行性。这部分主要在Matlab/Simulink平台完成。文献［12-15］中的热模型见图6。

3 实验结果与分析

3.1 内阻估计结果与分析

通过燃料电池系统中电流密度传感器和输出电压传感器等设备的工作，相应的数据监测值由CAN网络传输至FCU。在FCU内部设定的内阻估计程序中，将燃料电池输出电流密度作为扰动值，并结合内阻初始值和相应的参数进行内阻估计的实时在线迭代过程。内阻估算结果被传输至上位机保存。在FTP工况中，燃料电池输出电流密度和欧姆内阻见图7，燃料电池输出电流密度和仿真电压见图8。

在此模拟工况中，燃料电池的欧姆内阻范围为0.331 22～0.419 56Ω。可以看出，燃料电池欧姆内阻的波动较为剧烈，但燃料电池欧姆内阻的波动范围较小。燃料电池欧姆内阻值快速变化的直接原因是燃料电池电流密度的波动。在图8中，两者之间的关系为反比例关系，造成这种现象的原因包括：

1）燃料电池输出密度增加时，各单体内部化学反应迅速，阴极处有大量水产生，而阳极处的水含量少，便会在浓度差的作用下发生水分的渗透现象，从而使燃料电池内部的质子交换膜、催化剂得到相应的增湿，化学反应效率提高，内阻降低。

2）燃料电池输出上升时，反应气体的流量会相应提高，同时反应气体的压力增大。反应物压力增大会在一定程度上对燃料电池的输出性能起促进作用，使燃料电池的效率提高，极化曲线斜率降低，欧姆内阻相应降低。

3）当燃料电池输出密度降低时，反应物也会随之降低，但是空压机和氢气供应设备的响应较慢于燃料电池输出电流密度的下降，反应物较大的流量和压力会带走大量的水分，同时燃料电池输出电流密度的降低会减缓燃料电池内部水的产生，欧姆内阻有增大趋势。

对内阻估计算法进行验证，比较燃料电池的实测输出电压与采用估计内阻计算出的燃料电池输出电压。输出电压误差的仿真结果如图9所示。

从图9可以看出，误差为1.1%～1.5%，证明了内阻估计算法的准确性，但在燃料电池电流密度波动时误差变化迅速。

3.2 热模型热功率计算与分析

上述建立的燃料电池热功率数学模型中，热功率计算值去除了废气带走的热量和电堆自身的热辐射值。基于内阻的热模型计算的热功率和文献中经过校正的热模型功率值如图10所示。

从图10中可以看出，两者具有极高的一致性。表3展示了内阻估计值、热模型计算值和文献热模型计算值的部分数据。欧姆内阻和基于内阻热功率见图11。

基于内阻建立燃料电池热模型对计算燃料电池热功率具有较高的可行性，同时可间接证明基于卡尔曼滤波估算燃料电池欧姆内阻的准确性。燃料电池热功率在高电流密度输出情况下较高。受输出扰动的影响，在燃料电池功率变化时，基于内阻的燃料电池热功率高于文献热模型热功率计算值。

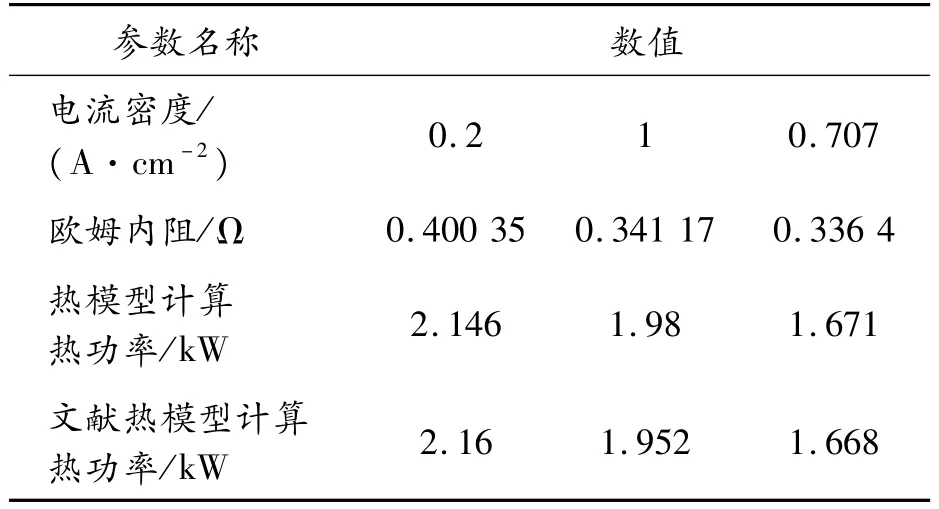
表3 内阻估计值、热模型计算值和文献热模型计算值的部分数据

4 结论

1）证明了基于欧姆内阻建立燃料电池热模型的可行性，为建立燃料电池热管理的控制策略拓宽了思路。

2）将燃料电池产热功率与运行内阻联系起来，可为燃料电池冷却液循环系统提供依据，即通过调节冷却液流量和散热器功率，将燃料电池的温度控制在合理范围内，保护燃料电池内部结构，维持良好的使用性能。

3）运用估算内阻计算输出电压与实测输出电压进行比较，证明了卡尔曼滤波算法的应用价值。燃料电池在大电流密度情况下，欧姆内阻相对较小，反之欧姆内阻则较高。此现象与燃料电池内阻产水量有较大关系。