基于平方根UKF的伪卫星动态跟踪定位算法
段晨浩 王珏 邓志鑫


摘 要: 为了解决传统Kalman滤波在处理非线性系统时的局限性,以及扩展Kalman滤波(EKF)在处理强非线性系统时发散性和精度较差的问题,结合动态导航系统中的目标跟踪定位问题,在不敏Kalman滤波(UKF)算法的基础上,提出了一种基于平方根UKF的动态跟踪定位算法,在递推运算过程中采用协方差矩阵的平方根代替传统算法计算过程中的协方差矩阵。MATLAB仿真结果表明,平方根UKF算法的精度比EKF提升了54.7%,比UKF提升了14.8%。所提出的算法解决了Kalman处理非线性系统的局限性以及传统EKF和UKF算法精度不高的问题,为伪卫星系统的高精度定位研究提供了有力支撑。
关键词: 算法理论;动态定位跟踪;伪卫星;平方根滤波;卡尔曼滤波算法;非线性
中图分类号:TN967.1文献标识码: A
doi:10.7535/hbkd.2020yx06003
Pseudolite dynamic tracking and positioning
algorithm based on square root UKF
DUAN Chenhao1, WANG Jue1, DENG Zhixin1,2
(1.The 54th Research Institute of CETC,Shijiazhuang,Hebei 050081,China;2.State Key Laboratory of Satellite Navigation System and Equipment Technology,Shijiazhuang, Hebei 050081,China)
In order to solve the limitation of traditional Kalman filter in dealing with nonlinear system and the problem of divergence and poor accuracy of extended Kalman filter (EKF) in dealing with strong nonlinear system, a dynamic tracking and positioning algorithm based on square root UKF was proposed based on the unscented Kalman filter (UKF) algorithm in combination with the problem of target tracking and positioning in dynamic navigation system. In the process of recursive operation, the square root of covariance matrix was used to replace the covariance matrix in the calculation process of covariance algorithm. The MATLAB simulation results show that the accuracy of the square root UKF algorithm is 54.7% higher than that of the EKF algorithm, and 14.8% higher than that of the UKF algorithm. The proposed algorithm solves the limitation of Kalman processing nonlinear system and the problem of the low accuracy of traditional EKF and UKF algorithms, and provides a strong support for the high-precision positioning of pseudolite system.
algorithm theory; dynamic positioning and tracking; pseudolite; square root filtering; Kalman filter algorithm; nonlinearity
為了解决传统卫星星座在某些特定区域(如峡谷、隧道、密林等)受地形遮挡[1]定位授时精度难以达到要求以及信号功率相对较弱容易受到复杂环境影响干扰欺骗的问题,作为一种区域增强系统,伪卫星能有效弥补卫星信号受遮挡的问题,并提供较强的导航信号。近几年,空基伪卫星成为研究热点。相比于陆基伪卫星,空基伪卫星虽有着更加灵活、应用场合更为多样、覆盖区域更广的优势,但也面临着诸多问题[2-4]。
空基伪卫星这一动态平台的自身位置对整个系统的定位精度有着重要影响。针对动态系统的定位跟踪,常采用Kalman滤波算法及扩展Kalman滤波算法。一般而言,Kalman滤波算法或者在其基础上演变的相关算法,在处理线性或者弱非线性系统方面效果较为理想,但对于较为复杂的非线性系统,其处理结果对于较高精度的动态跟踪定位来说很难达到要求[5-7]。针对上述问题,本文提出一种基于平方根UKF的动态目标跟踪定位算法,并与常见的EKF以及UKF算法进行仿真分析对比。
1 传统跟踪定位算法
空基伪卫星动态平台在运动过程中,伪卫星飞行状态之间、状态与观测量之间存在严重的非线性关系,因此需要采用非线性滤波技术得到其状态变量的最优估计值,将滤波算法运用到动目标跟踪定位中,通过引入滤波方法对动目标的行进路线进行预测与估计。常见的用于目标跟踪定位算法的滤波方法有Kalman滤波算法、EKF算法和UKF算法。
1.1 Kalman滤波算法
Kalman滤波是根据一定的滤波准则,采用最优化估计方法对观测系统的状态进行估计与预测的一种最优估计或最优滤波。其思路是在估计过程中,用上一次的最优状态估计和最优误差估计计算这一次的先验状态估计和先验误差估计,再用得到的先验误差估计以及量测噪声得到Kalman增益,结合前面所得到的先验估计和Kalman增益得到本次的最优估计,不断重复这个过程,用本次的最优估计来估算下一次的先验估计[8-9]。
假设动态系统的状态空间模型为
X(t+1)=ΦX(t)+ΓW(t),
Y(t)=HX(t)+V(t),
式中:X(t)为系统在时刻t的状态;Y(t)为对状态的观测值;W(t)为系统噪声,其方差矩阵为Q;V(t)为观测噪声,其方差阵为R;Φ为状态转移矩阵;H为观测矩阵;Γ为系统噪声驱动矩阵。Kalman滤波的计算流程如下。
计算状态一步预测:
[AKX^](t+1|t)=Φ[AKX^](t|t);
计算新息:
ε(t+1)=Y(t+1)-H[AKX^](t+1|t);
计算状态估计值:
[AKX^](k+1|k+1)=[AKX^](k+1|k)+K(k+1)ε(k+1);
计算Kalman滤波增益:
K(t+1)=P(t+1|t)HT[HP(t+1|t)HT+R]-1; (1)
计算一步预测均方误差:
P(t+1|t)=ΦP(t|t)ΦT+ΓQΓT; (2)
计算一步预测估计均方误差:
P(t+1|t+1)=[In-K(t+1)H]P(t+1|t)。 (3)
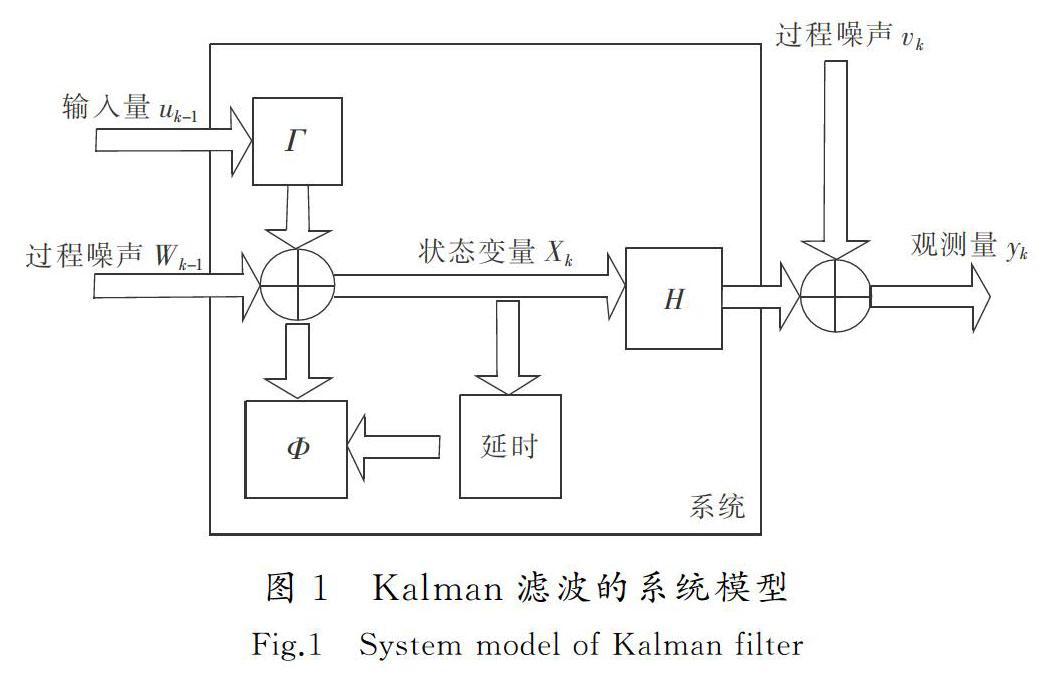
为了更形象地说明Kalman滤波原理,图1给出了Kalman滤波的系统模型框图。
1.2 EKF以及UKF滤波算法
Kalman滤波在处理线性高斯模型以及弱非线性系统时有着比较理想的效果,误差显著减少,但是在处理较强非线性系统时其滤波效果大部分情况下很难满足要求。而在实际应用场景即空基伪卫星在飞行过程中存在严重的非线性问题,此时常采用EKF以及UKF滤波方法对动目标的行进路线进行预测与估计[7]。
EKF的基本思路是围绕滤波值将非线性函数f(*)和h(*)展成Taylor级数,将一般的非线性系统处理为一个线性化系统的模型,再使用上述提到的传统Kalman滤波进行滤波处理[10]。但是Kalman滤波存在数值稳定性以及模型偏差等问题,同时又要求系统模型和系统噪声的统计特性精确已知,因此当系统具有较强的非线性或者初始误差较大时,EKF的滤波精度就会明显下降,甚至会出现发散[11]。
不敏Kalman滤波器(UKF)是针对非线性系统的一种改进型Kalman滤波器,采用Kalman线性滤波框架,对于一步预测方程使用不敏(UT)变换解决协方差以及均值的非线性处理问题。UKF实质上不是对非线性函数进行近似,而是对非线性函数的概率密度分布进行近似,同时也不需要对Jacobian矩阵求导,没有忽略高阶项,这就使得UKF克服了EKF精度低、稳定性差的缺点[11]。
UT变换与线性化方法的比较如图2所示。
2 平方根UKF滤波算法
在传统UKF滤波算法中,需要对每个采样点进行非线性变换,计算量比较大,而且数值计算的误差也比较明显,估计误差协方差矩阵的非负定性和对称性会因此受到影响,从而影响滤波算法的收敛速度以及稳定性[12]。为了提高滤波算法的滤波效率以及滤波精度,在递推运算过程中采用协方差矩阵的平方根来代替传统算法计算过程中的协方差矩阵,这种方法称为平方根不敏Kalman滤波算法[12]。
由式(1)—式(3)及初始值[AKX^]0=E[X0],P0=E[(X0-[AKX^]0)(X0-[AKX^]0)T],根据定义,在这里Pk及其预测Pk,k-1至少是非负定的,但是在舍去误差的情况下,很难保证这一点。因此,在递推过程中将Pk的递推式改为Pk平方根Sk的递推式,从而建立平方根滤波方程。
2.1 Pk的平方根递推方程
根据定义,Pk-1具有对称非负定性,设
Pk-1=Sk-1STk-1,
于是
Pk/k-1=Φk/k-1Pk-1ΦTk/k-1=Φk/k-1Sk-1STk-1ΦTk/k-1=Sk/k-1STk/k-1,
将式中的Sk/k-1=Φk/k-1Sk-1代入到式(3)中,
Pk=[I-KkHk]Pk/k-1=Sk/k-1{I-STk/k-1HTk[HkSk/k-1STk/k-1HTk+Rk]-1HkSk/k-1}STk/k-1, (4)
记Fk=STk/k-1HTk,式(4)可写成
Pk=Sk/k-1{I-Fk[FTkFk+Rk]-1FTk}STk/k-1=Sk/k-1[I-akFkFTk]STk/k-1,
式中ak=[FTkFk+Rk]-1。
2.2 平方根濾波方程
平方根滤波方差可写为
[AKX^]k=Φk/k-1[AKX^]k/k-1+Kk[Zk-HkΦk/k-1[AKX^]k-1],
[AKX^]0=E[X0],
Kk=akSk/k-1STk/k-1HTk=akSk/k-1Fk,
Fk=STk/k-1HTk,
Sk/k-1=Φk/k-1Sk-1, P0=S0ST0,
Sk=Sk/k-1[I-akrkFkFTk], rk=11±akRk。
根据以上平方根滤波方程进行滤波,每一步得到的Pk以及Pk/k-1至少是非负定的。
根据平方根滤波的原理,可以得到平方根UKF的滤波过程如下。
1)初始化
[AKX^]0=E[X0],SX0=sqrt(E[(X0-[AKX^]0)(X0-[AKX^]0)T])。
系统的初始增广状态变量为
[AKX^]a0=E[Xa]=[[AKX^]T0 [AKW-]T [AKV-]T]T,
系统
Sa0=sqrt(E[(Xa0-[AKX^]a0)(Xa0-[AKX^]a0)T])=SX0
SW
SV。 (5)
式中:W和V分别为系统过程噪声以及观测噪声向量;SW=RW,RW为过程噪声协方差矩阵;SV=RV,RV为观测噪声协方差矩阵。
2)对于k=1,2,3的实现步骤
计算Sigma点向量:
ξak-1=[[AKX^]ak-1 [AKX^]ak-1+γSaXk-1 [AKX^]ak-1-γSaXk-1]。
计算权值和参数:
γ=n+λ,
ω(m)0=λλ+n,
ω(c)0=ω(m)0+(1-α2+β),
ω(c)i=ω(m)i=12(n+λ), i=1,2,…,2n,
式中:λ=α2(n+κ)-n为复合刻度参数;n为增广状态向量的维数;α为决定先验均值周围Sigma点分布广度的主要刻度因数;β为强调验后协方差计算的零阶Sigma点权值的第二刻度因数;κ为第三刻度因数。
计算时间更新方程:
ξXk,k-1=f(ξak-1,ξWk-1, uk-1),
[AKX^][AKk-]=∑2ni=0ω(m)iξXi,(k,k-1),
S[AKX-]k=qr{[ω(c)1(ξX(1∶2n),(k,k-1)-[AKX^][AKk-])]},
S[AKX-]k=cholupdate{S[AKX-]k,ξX0,(k/k-1)-[AKX^][AKk-],ω(c)c},
χk,k-1=h(ξXi,(k/k-1), ξVk-1),
[AKZ^][AKk-]=∑2ni=0ω(m)iχi,(k/k-1)。
计算观测更新方程:
Sk=qr{[ω(c)1(χ(1∶2n),(k/k-1)-[AKZ^][AKk-])]},
Sk=cholupdate{Sk, χ0,(k/k-1)-[AKZ^][AKk-],ω(c)c},
PXkZk=∑2ni=0ω(c)i(ξXi,(k,k-1)-[AKX^][AKk-])
(χi,(k,k-1)-[AKZ^][AKk-])T,
Kk=(PXkZk/STk)/Sk,
[AKX^]k=[AKX^][AKk-]+Kk(Zk-[AKZ^][AKk-]),
U=KkSk,
SXk=cholupadate{S[AKX-]k,U,-1}。
式中:线性代数运算符“”表示利用下三角Cholesky分解得到的矩阵方根;qr(A)表示对矩阵A进行qr分解得到的下三角部分R矩阵;cholupdate{R,U,±V}表示矩阵(R±VUU)的Cholesky分解。
3 仿真分析
3.1 Kalman性能仿真分析
仿真条件设置如下:从初始位置X0(0,0)以X方向2 m/s,Y方向20 m/s的速度行进,时间总长为80 s,图3、图4分别为线性状态及非线性状态2种场景下Kalman滤波的跟踪轨迹及误差情况。
由图3可以看出,Kalman滤波在处理线性及弱非线性时的效果较为理想,误差显著减小。由图4可以看出,当处理较强线性处理效果不太理想时,Kalman滤波几乎没有什么效果,噪声也太大,随机扰动性增大导致”无规律可循”。
3.2 EKF,UKF及平方根UKF滤波性能对比分析
图5是3种算法的非线性定位跟踪效果,图6是3种算法的非线性定位跟踪误差,表1示出了估计误差均方差及运行时间,图7是95%置信区间下平方根UKF的跟踪定位效果。
由图5及图6可以较为明显地看出,在较强的非线性条件下,EKF的滤波精度较差且会出现明显的发散情况;图7在
95%的置信区间平方根UKF的大部分真实值都可以遍历到。由表1 可以看出,EKF估计误差均方差为9.640 3 m,虽然小于10 m但还是有明显差距。UKF的估计误差均方差为5.090 0 m,平方根UKF估计误差均方差为4.366 2 m,相比于EKF精度提升了54.7%,相比于UKF精度提升了14.8%。
在滤波过程中,不计算协方差矩阵及其预测,而是计算其平方根,虽然提升了精度以及稳定性,但会引起计算量的提升,EKF算法的运行时间为0.657 s;UKF算法的运行时间为0.723 s,平方根UKF算法的運行时间为 1.044 s。
4 结 语
1) 在滤波过程中采用协方差矩阵的平方根代替协方差矩阵参与递推过程,保证了递推过程中的稳定性。
2) 与EKF以及UKF相比,利用本文提出的以平方根Kalman滤波算法的动态定位跟踪算法,解决了发散问题,精度也有了较明显的提升。
3)本研究解决了Kalman处理非线性系统的局限性以及传统EKF和UKF算法精度不足的问题,为伪卫星系统的高精度定位提供了有力的支撑。
4) 由于递推过程中计算量的增加,使得算法运行时间有所增加,后续将在算法稳定性及运算速度方面进行深入探讨。
参考文献/References:
[1]李占营. 基于伪卫星技术的室内定位系统硬件设计及实现[D].成都:电子科技大学,2018.
LI Zhanying. Hardware Design and Implementation of the Indoor Positioning System Based on Pseudo Satellite Technology[D].Chengdu: University of Electronic Science and Technology of China,2018.
[2] 李坤.北斗伪卫星系统高精度定位关键技术研究[D].成都:电子科技大学,2018.
LI Kun. Key Techniques for High Accuracy Positioning of Beidou Pseudolite System[D].Chengdu: University of Electronic Science and Technology of China,2018.
[3]谢瑞煜,孙瑾.伪卫星辅助复杂地形卫星标定方法研究[J].现代防御技术,2019,14(5):22-28.
XIE Ruiyu,SUN Jin. Calibration method of pseudo-satellite assisted satellite incomplex terrain[J]. Modern Defence Technology,2019,14(5):22-28.
[4]史海青.北斗伪卫星空基增强网络优化与高精度动态时间同步[D].南京:南京航空航天大学,2014.
SHI Haiqing.Research on Enhancement Network Optimization and Precise Timing Synchronization for Air-borne Pseudo-satellites of Beidou[D]. Nanjing:Nanjing University of Aeronautics and Astronautics,2014.
[5]邹俊成.GNSS接收机中卡尔曼滤波的研究[D].广州:广东工业大学,2015.
ZOU Juncheng. Research of Kalman Filtering in GNSS Receiver[D].Guangzhou:Guangdong University of Technology,2015.
[6]周成松.GNSS 导航中卡尔曼滤波优化算法研究[D].长沙:国防科学技术大学,2016.
ZHOU Chengsong. Research on Kalman Filtering Optimized Algorithms in GNSS Navigation[D].Changsha: National University of Defense Technology,2015.
[7]毛秀華,吴健.卡尔曼滤波算法研究[J].舰船电子对抗,2017,40(3):64-68.
MAO Xiuhua,WU Jian. Research into Kalman filter algorithm[J].Shipboard Electronic Countermeasure,2017,40(3):64-68.
[8]黄小平,王岩.卡尔曼滤波原理及应用[M].北京:电子工业出版社,2015.
[9]杨元喜.动态Kalman滤波模型误差的影响[J].测绘科学,2006,31(1): 17-18.
YANG Yuanxi. Influence of dynamic Kalman filter model error[J].Science of Surveying and Mapping,2006,31(1): 17-18.
[10]冯亚丽.非线性卡尔曼滤波算法的改进及精度分析[D].重庆:西南大学,2017.
FENG Yali. Improvement and Accuracy Analysis of Nonlinear Kalman Filtering Algorithms[D].Chongqing:Southwest University,2017.
[11]叶松庆.非线性卡尔曼滤波算法研究[D].北京:中国科学院大学,2016.
YE Songqing. Research of Nonlinear Kalman Filtering Algorithm[D].Beijing: University of Chinese Academy of Sciences,2016.
[12]王海春,贾小林,李鼎. 北斗三号卫星广播星历精度评估分析[J].导航定位学报,2019,7(4):60-63.
WANG Haichun,JIA Xiaolin,LI Ding. Accuracy assessment and analysis of broadcast ephemeris of BDS-3 satellites[J]. Journal of Navigation and Positioning,2019,7(4):60-63.
[13]KAZMIERSKI K,SO[KG-*4]S[DD(-*2]'NICA K, HADAS T. Quality assessment of multi-GNSS orbits and clocks for real-time precise point positioning[J].GPS Solutions,2018,22(11):678-683.
[14]BRADLEY W. Near-optimal low-thrust earth-mars trajectory via a genetic algorithm[J].Journal of Guidance,Control and Dynamics,2015,28(5):1027-1031.
[15]CHANDRA K P B,GU D W,POSTLETHWAITE I.Square root cuba-ture information filte[J].IEEE Sensors Journal,2013,13(2):750-758.
[16]VO B T,VO B N,CANTONL A.The cardinality balanced multi-target multi-bernoulli filter and its implementation[J]. IEEE Transactions on Signal Processing,2009,57(2):409-423.
[17]VO B N,VO B T.Labeled random finite sets and the multi-object conjugate priors[J]. IEEE Transactions on Signal Procession,2013,61(13): 3460-3475.
[18]王海环,王俊. 一种改进的多伯努利多目标跟踪算法[J].西安电子科技大学学报,2016,43(6): 176-182.
WANG Haihuan,WANG Jun.Multi-target tracking with the cubature Kalman multi-bernoulli filter[J].Journal of Xidian University,2016,43(6):176-182.
[19]张栋,焦嵩鸣,刘延泉. 互補滤波和卡尔曼滤波的融合姿态解算方法[J]. 传感器与微系统,2017,36(3):62-65.
ZHANG Dong, JIAO Songming,LIU Yanquan. Fused attitude estimation algorithm based on complementary filtering and Kalman filtering[J]. Transducer and Microsystem Technologies,2017,36(3): 62-65.
[20]谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2012.
[21]王见,马建林.EKF与互补融合滤波在姿态解算中的研究[J].传感技术学报,2018,
31(8): 1187-1191.
WANG Jian,MA Jianlin. Research on attitude algorithm of EKF and complementary filtering fusion[J]. Chinese Journal of Sensors and Actuators, 2018,31(8): 1187-1191.
[22]张苏英,赵国花.基于改进的蚁群算法的移动机器人路径规划[J].河北工业科技,2019,36(6):390-395.
ZHANG Suying,ZHAO Guohua. Path planning of mobile robot based on improved ant colony algorithm[J]. Hebei Journal of Industrial Science and Technology, 2019,36(6):390-395.

