基于海洋性专业人才培养的高等数学教学改革研究

刘祖林 何家洪 宋翌

摘 要：高等数学是理工科和经济管理等专业的公共基础课，它对学生专业的发展起着至关重要的作用。学生高数水平的高低很大程度上影响了学生专业的发展。目前，高等数学在教学过程中还存在一些问题。本文以北部湾大学海洋性专业18、19级的学生为研究对象，首先通过问卷调查获取影响学生高数水平的因素，然后采用层次模糊综合评价法进行分析，最后根据影响因子综合评价指标的优先级给出基于海洋性专业人才培养的高数教学改革的建议。

关键词：海洋性专业;层次模糊综合评价法;影响因子;综合评价指标优先级;建议

一、课题研究的现状和意义

高等数学是高校中衔接的专业门类较广且接触的学生数量较庞大的一门公共基础课程。由于它的内容比较抽象且逻辑推理较强，它给学生的学和教师的教带来了很大的困难。但高数是很多专业的基础，学生高数水平的高低对其专业的发展起着至关重要的作用。因此，高校需要不断地完善高数的教学改革，以便满足学生专业发展的需求。目前，很多学者基于特色专业人才的培养对高数的教学改革进行了研究，并给出了相应的改革建议[1-3]。但是，当前的高数在教学过程中仍存在着一些问题：高数的任课教师不了解高数与所授课学生专业的相关性，在教学过程中不能把高数与学生的专业紧密地结合;教师的教贯穿了整个课堂，忽视了学生是课堂的主体，缺少了与学生之间的互动，不了解学生的学习方式和思维模式;针对不同专业的学生，任课教师选用了相同的教材和制定了相同的教学计划，缺乏了考虑学生的数学基础和专业的差异性，形成了无差异的教学;考核方式单一，很多高校都采用了（平时10%+期中30%+期末60%）的考核方式，一定程度上影响了学生课堂学习的积极性和对知识的渴望;部分任课教师为了完成教学任务，过于依赖PPT，对新的概念照本宣科，成为了定理证明过程的搬运工，对学生着重强调计算而忽视了知识背景的重要性以及对新概念的理解和定理的证明;上述问题很大程度地制约着任课教师高数教学水平的提升，影响了学生专业的发展。

海洋性专业具有区域性的特点，它对沿海城市经济的发展举足轻重。它的健康发展不仅可以加快地方经济发展的进程，同时可以辐射周边的城市，带动周边城市经济的快速发展。高等数学作为海洋性专业的基础课程，它的健康发展对海洋性专业的发展起着至关重要的作用。通过对基于海洋性专业人才培养的高数教学现状进行研究分析，寻找任课教师在教学过程中存在的问题，了解学生对高数知识的需求，才能更好的对高数的教学进行改革和建设，为高校的特色专业制定人才培养方案和专业课程的建设提供有价值的参考性建议，为社会培养高质量的人才具有积极的意义。

二、基于海洋性专业人才培养的高数教改的调查与分析

本文以北部湾大学的特色专业海洋性专业（海洋、海运、机械与船舶海洋工程）18、19级的学生为调查对象，发放300份问卷，有效收回285份。问卷的主要目的是研究学生自身和任课教师两个方面对学生高数水平发展的影响因素，为高数的教学进行改革研究提供依据。问卷的内容主要分为两部分，一是学生自身因素，二是任课教师对学生的影响因素。第一部分主要包含学生对高等数学与专业相关性的认知，对高等数学难易度的感知以及学生的学习方式和学习时间对学生高数水平的影响程度;第二部分主要包含教师对教材与教学内容的选择、考核方式以及课堂氛围对学生高数水平的影响程度。

本文主要采用模糊综合层次分析法，建立相应的层次模型对问卷数据进行分析处理，给出影响因子的模糊判断矩阵，通过加权平均算术的方法获得各个影响因子的隶属度以及综合隶属度，最后根据各级影响因子评价指标隶属度的优先级做出判定，并给出相应的结论和建议。建立具体的模糊层次结构如下：

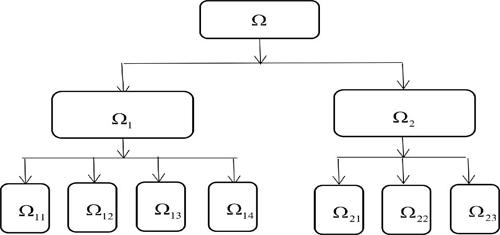
目标层：高等数学的综合影响因子Ω

准则层一级指标：学生Ω1，教师Ω2;

准则层第一个二级指标：高数与专业相关性的认知Ω11，高数的难易度Ω12，学习方式Ω13，学习时间Ω14;

准则层第二个二级指标：教材与内容的选择Ω21，考核方式Ω22，课堂氛围Ω23;

根据各个影响因子对学生高等数学水平的影响程度，类似文献[4]给出了五个等级评价指标：影响大、影响较大、影响一般、影响较小、没有影响，构成评语集          。

通常在实际中，很难给出任意两个影响因子两两比较的精确值。为了更合理的描述任意两个影响因子之间的偏好关系，学者们采用了模糊数去量化不确定的因素[5-6]。如区间模糊数表示为      ，当   时，表示指标aj优于ai;当

时，表示指标ai优于aj;当   且   时，表示ai优于aj在

与 之间;当     时，表示ai与aj优先级相等。通过对各级影响因子进行两两比较构造的一级影响因子的区间模糊互补矩阵如下：

第一个二级影响因子的区间模糊互补矩阵：

第二个二级影响因子的区间模糊互补矩阵：

根据文献[7]，从区间模糊互补判定矩阵中构造两个互补判定矩阵        ，其中

利用公式（1）从区间模糊互补判定矩阵A，B，C中分别得到互补判定矩阵A1，A2，B1，B2，C1，C2如下：

根据文献[8]-[9]的方法，利用下列公式：

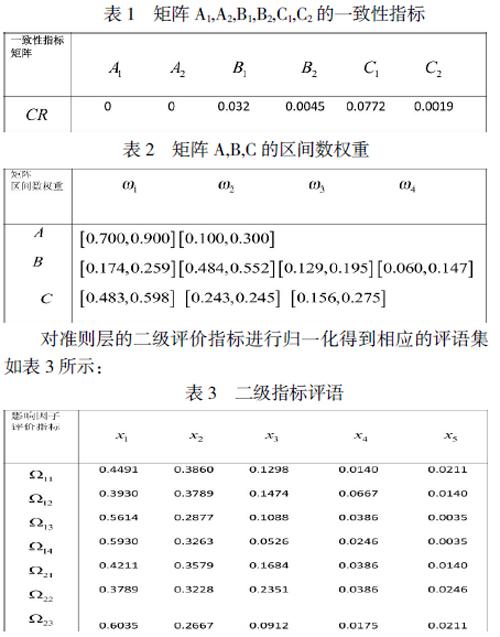
得到判定矩阵A1，A2，B1，B2，C1，C2的一致性指标和A，B，C的区间数权重如表1和表2所示：

对准则层的二级评价指标进行归一化得到相应的评语集如表3所示：

从表1可知，互补判决矩阵的一致性指标均小于0.1，因此各判段矩阵均具有满意近似一致性，从而可知矩阵A，B，C均具有滿意近似一致性。

从表3中分别获得第一个和第二个二级影响因子的指标的判定矩阵如下：

利用如下公式：

其中，                     ，

得到第一个和第二个二级影响因子的区间数综合评价指标分别为：

利用文献[10]的可能度公式，得相应的可能度矩阵分别为：

根据区间数的可能度矩阵可知，第一个和第二个二级影响因子的评价指标优先级分别为：            。

一级影响因子对目标层的综合评价指标为：

通过计算得到的可能度矩阵为：

得到目标层影响因子的综合评价指标优先级为：

三、基于海洋性专业人才培养的高数教学改革的总结与建议

（1）根据影响因子综合评价指标隶属度的优先级，我们获得影响学生高数水平的结论如下：

a：目标层影响因子的评价指标E1和第一个二级影响因子的综合评价指标E2隶属度的优先级一样，其中最优隶属度为影响大，说明了学生自身对高等数学与专业相关性的认知以及高等数学难易度的感知，学生的学习方式和学习时间对学生高数水平的发展影响非常大。

b：第二个二级影响因子的综合评价指标E3与目标层影响因子的评价指标E1隶属度的优先级一样，最优隶属度均为影响大，说明了教师对学生专业教材以及教学内容的选择，对学生的考核方式以及营造的课堂氛围对学生高数水平的发展影响也非常大。

上述结论表明学生自身和任课教师对学生高数水平的发展都有非常大的影响。根据问卷调查分析可知，当前，我校基于海洋性专业人才培养的高等数学在教学过程中还存在一些问题：

①任课教师在教学过程中，针对不同的专业选用了相同的教材和制定了相同的教学计划，没能充分地与学生专业知识紧密的结合授课，使得学生缺乏对高等数学与专业相关性的认知，如海洋性专业的流体力学问题与高数知识的关联性;

②教师缺乏了解学生的学习方法和思维模式，没能给与学生恰当的指导。部分学生不适应大学课堂的上课方式，在学习过程中套用以前的学习方法，即只注重公式的记忆和应用。通常为达到巩固知识的目的而花大量的时间进行题海战术，却经常忽视了理清知识点的来龙去脉，理解概念的含义以及定理的证明思想;

③考核方式比较单一，如平时成绩占10%（上课+作业），期中30%，期末60%。平时成绩比值偏小且考核单一，影响了学生参与到课堂问答环节的积极性，增加了任课教师了解学生对知识的理解和掌握情况的困难，降低了课堂的教学质量和学生的学习效率;

④部分任课教师为了完成教学任务，对概念照本宣科和做定理证明过程的搬运工，课堂上缺乏与学生之间的互动，营造了枯燥乏味的课堂氛围，使得学生不能自控地睡觉，或开小差、玩手机等一些与课堂无关的事。这直接导致了学生学习效果差，增加了学生对高数的难度感，降低了学生学习的兴趣，挫伤了学生学习的积极性;

（2）针对上述存在的问题，给出基于海洋性专业人才培养的高等数学教学改革的建议：

①任课教师在教学过程中应了解高数与所授课学生专业的相关性，选用适合的教材和制定相应的教学计划，帮助学生提高高数与专业相关性的认知度。如海洋性专业中的流体力学问题，涉及到的高数内容主要有格林公式、高斯公式、斯托克斯公式等重要内容。在教学过程中应结合学生专业的具体实例进行分析和讲解，进一步加强学生的理解能力和对知识的掌握;

②任课教师应深入了解学生的学习方法、思维方式，并给与恰当性的指导。如建议学生先了解知识的背景，然后加强对概念的语言表述、逻辑关系的理解，掌握定义的核心思想;注意相关定理的前提条件，多问为什么，理清定理的因果关系，以便提高学生分析问题和解决问题的能力;

③改变单一的考核方式，把考核方式设置为平时30%（课堂问、答20%+课堂作业5%+课后作业5%）+期中20%+期末50%。通过增加课堂的问答和课堂作业环节，有利于調动学生参与课堂活动的积极性，提高课堂的教学质量;有利于学生及时地发现自身的问题，有利于教师及时地了解学生对知识的掌握情况;

④教师应做好课堂的充分准备，摆脱对PPT的过度依赖，丰富教学手段，加强课堂与学生之间的互动，帮助学生理解概念和定理的证明思路，增加课堂的趣味性，减少外界对学生的干扰，提高学生对高数的兴趣，降低学生对高数的难度感，提高学生的学习效率，增加学生学习的积极性。

上述调查结果分析表明，我校基于海洋性专业人才培养的高等数学在教学过程中还存在一些问题。但高等数学作为海洋性专业的基础，它对学生专业的发展起着至关重要的作用。因此，只有不断地完善高数的教学改革，才能更好地促进学生专业的发展，为国家和地方的发展输送高质量的人才，促进国家和地方经济的快速发展。

参考文献：

[1] 周江羽， 张晓军， 刘常青. 基于特色和品牌专业建设的新一轮本科教学体系改革——以资源勘查工程专业为例[J]. 中国地质教育， 2010（01）：68-71.

[2] 赵华杰. 基于专业发展的应用型院校高等数学教学改革研究[J]. 科技创新导报， 2019（14）.

[3] 边平勇. 基于应用型人才培养的高等数学教学改革探索[J]. 长春理工大学学报（社会科学版）， 2013（07）：205-206.

[4] 李红刚， 沈世云， 邹杨. 高等数学对学生个人发展影响的调查分析[J]. 重庆第二师范学院学报， 2014（03）：85-88.

[5] Xian S D . A new fuzzy comprehensive evaluation model based on the support vector machine[J]. Fuzzy Information and Engineering， 2010， 2（1）：75-86.

[6]姚敏， 黄燕君. 模糊决策方法研究[J]. 系统工程理论与实践， 1999， 19（11）：61-64.

[7] Liu F . Acceptable consistency analysis of interval reciprocal comparison matrices[J]. Fuzzy Sets and Systems， 2009， 160（18）：2686-2700.

[8] Saaty T L. A scaling method for priorities in hierarchical structures， Journal of Mathematical Psychology 15 （1977） 234–281.

[9] Xu Z S ， Cuiping W. A consistency improving method in the analytic hierarchy process[J]. European Journal  of Operational Research， 1999， 116（2）：443-449.

[10]Liu F ， Shang Y F ， Pan L H . A Modified TOPSIS Method for Obtaining the Associated Weights of the OWA-Type Operators[J]. International Journal of Intelligent Systems， 2015， 30（10）：1101-1116.

作者简介：

刘祖林（1990-），男，广西玉林，北部湾大学理学院，讲师。