基于改进神经网络的航班延误预测

陈兴瑞；何光勤

（中国民用航空飞行学院，广汉618307）

1 影响航班延误的因素

由于航班数量的不断增加、航空密度也在不断加大，航班延误问题日益凸显,导致航班延误的主要因素有天气原因、机械故障、交通流量控制等。

1.1 天气原因

能见度、雷雨区，强侧风是影响航空正常飞行的因素。如果出发地机场天气状况不适合飞行、目的地机场天气状况不适合降落、飞行航路上气象状况不适合飞行、因恶劣天气导致机场设施受损、跑道不够标准等都会造成航班延误。即使出发地阳光明媚，也可能因天气原因导致航班延误。

1.2 交通流量控制

我国为了确保国防安全，对空域使用范围实行了严格限制，军用空域占80%，民航方面可调节的范围只有20%。我国航班总量急剧攀升，而与之对应的地面设备、导航设备发展滞后，不能完全适应当前快速发展的民航业，航线结构不合理，造成空中塞车现象，所以流量是导致航空延误的一个无法忽略的原因。

1.3 机械故障

若飞机在登机前或飞行中出现机械故障，必须延迟登机或返航、就近降落，再按照维护程序进行必要的检查、分析，排除故障，检测安全性，或者安排其他航班运送旅客，都会造成航班延误。

2 神经网络简介

神经网络 （Back Propagation） 是以 Rumelhart 和McCelland 为首的一些科学家小组提出的，是目前应用最广泛的神经网络模型之一，这是一种按照误差反向传播算法训练的一种多层前置反馈网络。其中BP 网络能按照算法学习并存贮大量的输入-输出映射模式这种关系的网络，而且是不需要提前揭示描述这种映射关系的数学方程。神经网络是由输入层结构，输出层结构和一个或多个隐层节点结构互连而成的一种多层网络，这种特殊的结构使多层前馈网络结构可以在输入结构和输出结构间建立许多合适的线性或者一些非线性关系网络。

3 基于改进神经网络的航班延误预测模型建立

传统神经网络下降梯度慢，误差较大，为了避免这一问题的产生，采用了附加动量法进一步加快收敛的速度，减小结果误差。

3.1 向前传播阶段

①首先要从样本集中选取适当样本Pi，并将样本Pi输入网络；

②根据输入输出值计算出初步误差测度Ei和实际输出Ei=FL（…（F2（F1（PiW1）W2）…）WL）；

③然后再对权重值W1，W2，…WL各做一次调整，继续进行重复这个循环，直到∑Ei<ε。

3.2 向后传播阶段——误差传播阶段

①首先计算出实际输出值Ei与理想输出值Ei的差值；

②然后根据输出层输出的相对误差进一步调整输出层中的权矩阵结构；

3.3 附加动量项

在进行梯度下降搜索的时候，如果目前梯度下降和前面的一个梯度下降是相同方向，则进行加速搜索，相反就进行降速搜索。

式中Δω（t）是第t 次迭代市的对应的参数调整量，η为对应的学习率，g（t）为第t 次迭代时进行计算得出的梯度。式中 Δω（t）是第 t 次迭代的参数调整量，η 为学习率，g（t）为第t 次迭代计算出的梯度。

改进的神经网络在添加过动量项后，基于下降梯度的相关参数就进一步更新为：

Δω（t）=η[（1-μ）g（t）+μg（t-1）]Δω（t）=η[（1-μ）g（t）+μg（t-1）]

式中，μ 为动量因子（取值 0～1）。上式也等价于：

Δω（t）=αΔω（t-1）+ηg（t）Δω（t）=αΔω（t-1）+ηg（t）

式中 α 称为遗忘因子，αΔω（t-1）αΔω（t-1）表示上一次进行梯度下降的方向以及大小等信息对当前所处梯度下降的调整影响。

进一步用实际误差估计出与输出层直接相连接的前导层的先相对误差，再用和输出层连接前导层的相对误差进一步估计更前一层之间的误差。如此循环往复获得其他部分所有各层之间的误差估计值；并利用这些误差估计值实现对权矩阵的进一步修改。然后进一步形成一种将输出端的误差值沿着与输出信号完全相反的方向逐级向输出的过程中不断进行修正网络权值和阈值使误差函数沿负梯度方向下降，当逼近期望值时输出。隐层可以有一层或多层，图 1 是 m×k×n 的三层 BP 网络模型，网络选用 S 型传递函数通过反传误差函数用于函数逼近、模型识别分类、数据压缩和时间序列预测等不断调节网络权值和阈值使误差函数E 达到极小。

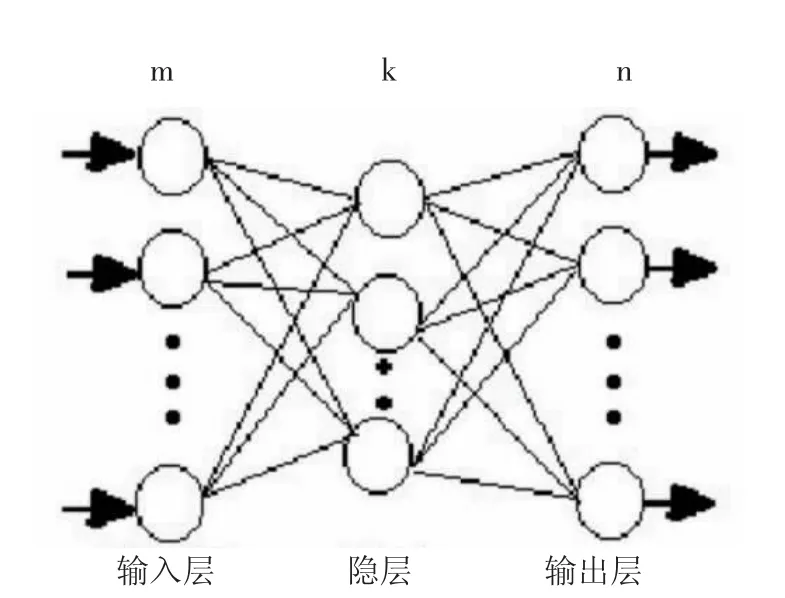
图 1 m×k×n 三层 BP 网络模

3.4 隐含层设计

根据有关研究表明，当系统含有单个隐层的神经网络时，如果神经网络系统中隐含节点数量足够多，那么可以用任意一个精度无限逼近一个非线性函数。因此，本文拟采用仅含有单个隐含层结构的三层结构多输入结构单输出的结构网络来建立延误预测模型。在进行网络设计的过程中，隐含层神经元数量的确定非常重要。如果隐含层中含有的神经元的个数较多，就会进一步加大网络计算的计算量并且容易发生过度拟合问题；隐含神经元个数较少时，就会进一步影响系统的网络性能，结果就是达不到之前预期想要的效果。神经网络中隐含层神经元的数量一定要结合要解决实际问题的复杂度来考虑，输入层结构的神经元数量和输出层结构的神经元数量以及对期望误差数值的大小的设定之间有着密切的联系。目前为止，关于隐层结构中神经元个数的确定还没有具体公式，最终选取了以下的经验公式

式中，n 表示为输入层神经元数量，m 表示为输出层神经元数量，其中a 为[1，10]之间的所有常数。该延误预测模型以五组天气情况数据指标作为输入层结构，以航班延误时间作为输出层结构，所以可以看出输入层的节点数量为5，输出层的节点数量为1，在本次实验中选择隐层神经元个数为2。

4 结语

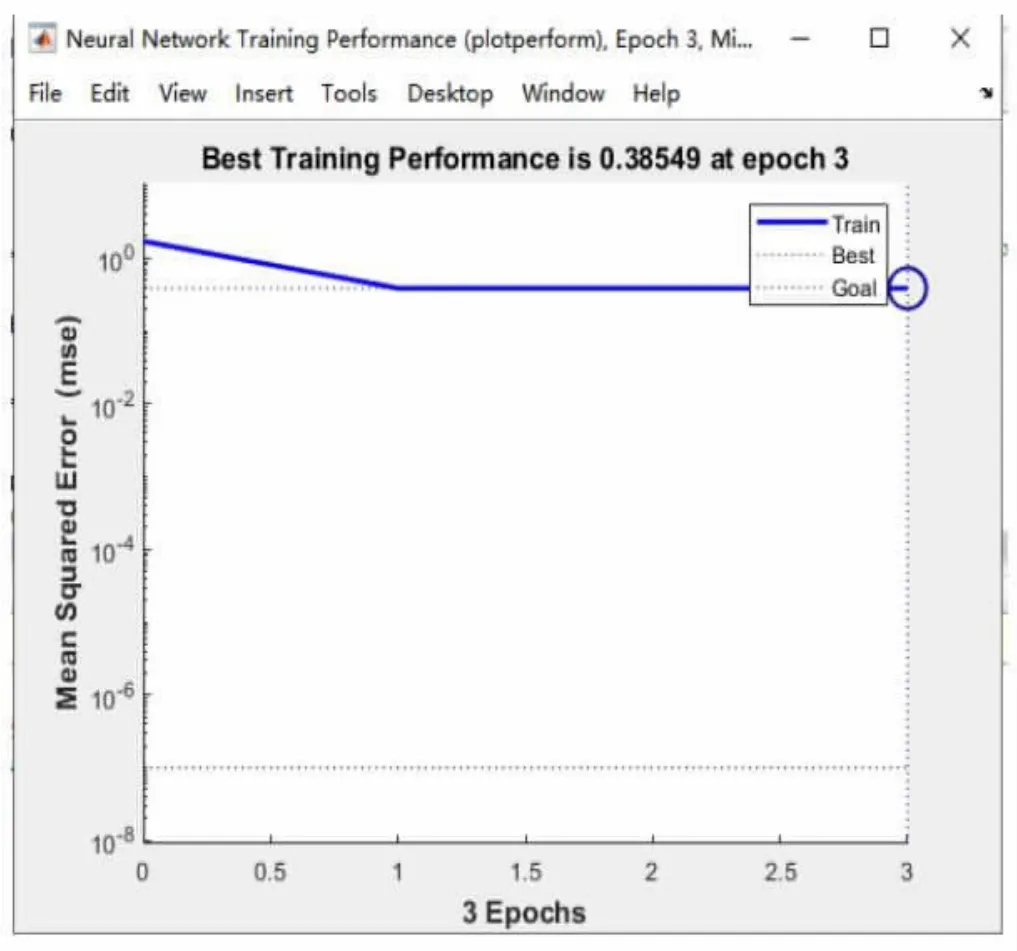
图2

改进型神经网络在进行处理训练的时候有时会陷入局部最小困局，也就是说误差变化很小，那么反馈信号对于权值的调整影响就会很小，但总误差计算出来又大于结果所设定的总误差。所以在这个时候增加入单个动量因子帮助其增大反馈的误差信号从而使神经元的权值重新开始振荡起来。对选取的样本数据进行训练后，根据结果可以看出此模型非常实用，校核方法从预测输出和期望输出的情况来看，改进的神经网络在一定程度上实现了对航班延误时间的判断，训练误差大大降低。