基于SINTAP转变区间内非均质材料断裂韧度预测方法
张亚林,惠 虎,黄 淞,周忠强,丛湘纯
(华东理工大学 机械与动力工程学院,上海 200237)
0 引言
核压力容器用铁素体钢(如SA-508,SA-738等)具有显著的韧脆转变现象,其断裂韧度值与温度的关系曲线分为:上平台、韧脆转变区和下平台。在韧脆转变区,断裂韧度随温度的下降而剧烈降低,且材料的断裂形式由延性断裂转变为脆性断裂。脆性断裂在断裂时并不会有明显的征兆,突然的失稳断裂会造成严重的安全隐患。核电一回路铁素体钢,长期遭受中子辐射材料的性能可能会大幅脆化,造成韧脆转变温度升高[1-3]。一旦材料力学性能下降到发生脆断的临界条件,处于高温高压下的反应堆压力容器会发生瞬时破坏[4]。因此,为保障反应堆压力容器的安全,必须确保材料的断裂韧度满足安全要求,这对于确保核电站安全可靠运行具有重要的现实意义。
铁素体钢由于断裂韧度的本质分散性[5],其韧性表征一直是工程上比较困难的问题。直到Wallin等[6-7]提出主曲线法,只需要通过断裂韧度试验确定一个参考温度T0,就可以得到不同累积失效概率下断裂韧度随温度的分布规律。然而,主曲线法只适用于宏观均匀的铁素体钢,这给非均质材料的韧性预测带来阻碍[8]。而高温高压下的反应堆压力容器(RPV)涉及很多典型的宏观非均质材料,如厚截面钢和焊接接头。厚截面钢由于在淬火的过程中可能会导致表面和心部显微组织差别较大,从而导致不同厚度方向力学性能有明显差异,其中脆性断裂韧度受组织敏感性更大。焊接热循环导致过热区的组织粗大劣化是焊接接头抗断裂的薄弱环节。因而,能准确表征非均质材料的断裂韧度,对保障承压设备的安全运行至关重要,尤其对存在辐照脆化风险的反应堆压力容器。在2019年新出版的ASTM E1921标准附录X5中提到了一种解决方案引起了笔者的关注,查阅后发现这版新增补的附录实质上是在1999年出版的欧洲结构完整性评价标准SINTAP上的改进,本文后续称为SINTAP法。然而查阅数据库,在国内有关非均匀材料转变区间的韧度预测却鲜有报道。
本文首先梳理SINTAP法的过程,并将复杂的数值过程通过MATLAB编程实现;然后结合国内外文献中的数据,探讨SINTAP法非均匀筛查中所存在的问题。以核电60 mm厚SA738Gr.B钢手工电弧焊焊接接头为研究对象,试验测得焊接接头母材、焊缝和热影响区的断裂韧度,并通过SINTAP法表征非均匀焊接接头3个区域韧脆转变区间的韧性分布,并和主曲线法的预测结果进行对比,为非均匀材料韧性预测给出合理的建议。
1 基于SINTAP改进的主曲线法
1.1 SINTAP法的步骤
SINTAP法主要是为了分析随机非均匀性材料的断裂韧度,其中包含3个步骤,每一个步骤的不同点在于用于数据分析的标准不一样。值得注意的是,SINTAP法依然是建立在主曲线法的两个前提假设之上,也即统计基础依然满足脆性断裂韧度在转变区间的分布符合三参数Weibll分布;经验基础依然满足断裂韧度和温度的关系曲线形状不变。SINTAP法中若使用单温度法,会得到一个下包络形状参数K0或者一个偏大值的参考温度T0;若使用多温度法,仅会得到一个偏大值的参考温度T0。综合的结果是,SINTAP法可以提供一个偏于保守的韧性估计,其原理主要是通过统计筛查的原理处理了非均质材料中韧性较好的那部分试验数据,因而它是一种适用于工程中结构完整性评价的方法。除此之外,SINTAP法还可以用于判断一组试验数据是否非均质。本文结合1999版的SINTAP和新出版的ASTM E1921—2019说明SINTAP法的步骤,并将复杂数值过程通过编程实现。
步骤1本质上是一个标准的主曲线法过程,其操作步骤可以参考标准ASTM E1921。这一步是用来检查断裂韧度数据的有效性,有效的数据可以依据主曲线法得到相关的参考温度T0(step1)或者K0(step1)。同时求出试验温度为Ti时,50%累计失效概率下的中值断裂韧度KJc(med)作为步骤2中的数据处理指标KCENSi,其公式如下:
KCENSi=30+70exp[0.019(Ti-T0(step1))]
(1)
步骤2是一个截尾(lower-tail)样本下的极大似然估计。比较经厚度换算为1T的KJci与KCENSi的相对大小。若KJci≥KCENSi,则令KJci=KCENSi,且检查常数δi=0;若KJci T0(step2-1)≥T0(step1)+0.5 (2) 步骤3是断裂韧度的最小值估计,对应的参考温度T0(step3)应为最大值。该步骤是试验样本较少时的预测方法,一般为试样数目N<9时。对于每一个δi=1,即符合有效性检验的等效1T试样的KJci值,可以通过公式(3)计算每个数据点的T0i,所有结果的最大值即为T0(step3)。 (3) 当第1.1节中的预测结果满足公式(4)时,则认为试验材料为宏观非均质的;反之,则认为材料是宏观均质的。均质材料的参考温度采用步骤1中的T0(step1);对非均质材料,若试样样本值大于9,则采用步骤2的T0(step2)作为材料的参考温度。若试样的样本容量小于9,对比步骤2和3中参考温度,若步骤3的结果比步骤2高出8 ℃,则采用步骤3的T0(step3)作为材料的参考温度,否则采用步骤2的T0(step2)作为材料的参考温度。 (4) 式中β——样本容量的不确定度因子,定义见ASTM E1921—2019中第10.10节; r——有效试样的数目。 为了探讨SINTAP改进的主曲线法用于预测非均质材料的适用性,本文以厚度60 mm核电用SA738Gr.B钢及其手工电弧焊焊接接头为研究对象,测试了母材、焊缝和热影响区的断裂韧度;将SINTAP复杂的数值和统计过程通过编程实现,并用于预测焊接接头不同区域处的参考温度T0及韧脆转变区间韧性分布情况。对比标准主曲线法和SINTAP改进主曲线法预测结果的差异,探讨非均质对韧性评估的影响。通过试验数据和文献调研发现SINTAP法中非均质筛查条件,可能会产生错误的结果。更进一步的讨论将于第3部分进行。 试验母材为SA738Gr.B钢,板厚为60 mm,属于低合金高强钢。出厂时为调质态,室温组织为粒状贝氏体加少量铁素体,这类钢具有明显的韧脆转变现象。焊接试板采用埋弧焊的焊接方法,其坡口和焊接顺序如图1所示。焊缝的长度为1 000 mm。 图1 焊接坡口和顺序示意 断裂韧度试验标准参考ASTM E1921—2019。母材采用厚度为1T的标准C(T)试样,数目为10个,板厚中面附近取样,宽度方向为横向裂纹扩展沿着轧制方向。由于材料的限制,焊缝和热影响区采用1T比例缩小的0.5T的C(T)试样,焊缝和热影响区试样皆为19个,取样方位为裂纹面沿着焊缝轴线且试样厚度方向和板厚一致,取样方案见图2。所有试样的裂纹由线切割机械加工的长度和疲劳试验预制的裂纹长度两部分组成,预制的疲劳裂纹接近2 mm,使裂纹的总长度和试样的宽度比a/w约等于0.5。 图2 取样位置示意 为了获得参考温度,试验温度的选取至关重要,依据前期的经验积累[9-10],母材试样选择在-147 ℃下进行,焊缝和热影响区试样选择在-70,-80 ℃下进行。整个试验的降温过程采用液氮喷淋的方式,试验温度和目标温度的误差不超过3 ℃。为了检验断裂韧度数据的有效性,保证所有数据结果接近高拘束情况,需要获取断裂韧度的上限值。因而,母材和焊缝处各选取3个拉伸试样,获取材料的基本性能参数。 表1列出不同试验温度下母材、焊缝和热影响区断裂韧度测试值。依据ASTM E1921的要求,将0.5T的断裂韧度结果转换成1T的结果,转换公式见式(5)。经有效性检查,仅热影响区有一个无效数据点,无效数据点检查常数δi取0。 KJc(1T)=20+(KJc(0.5T)-20)×0.841 (5) 表1 母材、焊缝和热影响区断裂韧度 有效性检查需要每个数据小于KJc(limit),KJc(limit)的计算公式如下: (6) 式中b0——初始韧带长度,mm; σys——室温下的屈服强度,MPa; E——弹性模量,GPa; Mlimit——无量纲变形极限,常取Mlimit=30; υ——泊松比。 若数据KJci>KJc(limit),则将KJc(limit)的数值赋予给KJci且检查常数变为0。参考ASTM E1921,将所有数据代入式(7)迭代计算出不同材料的参考温度T0。 (7) 依据第1.1节,自编程序可以得到3个步骤的预测结果,如表2所示。 表2 母材、焊缝和热影响区SINTAP法预测结果 (a)母材 从表2可以得到标准主曲线法的参考温度,其中母材为-145.03 ℃、焊缝为-69.38 ℃、热影响区为-145.66 ℃。这意味着焊缝金属是这个焊接接头的薄弱环节。热影响区和母材参考温度的数值相当且都比较小,说明热影响区性能劣化不严重。这和国内的一些低合金钢的测量结果不太一致,通常来说热影响区由于焊接热循环的作用应为韧性较差的部位。仔细分析后发现,在显微镜下,热影响区的宽度为3 mm左右,而粗晶区仅为0.5 mm。取样时尽管严格控制操作流程,也只能保证初始裂纹面位于热影响区,而具体是在热影响区的粗晶区还是细晶区是随机分布的。这就有可能导致落在韧性较好区域的试样较多,而韧性较差的粗晶区试样较少,从而导致热影响区整体的韧性偏高。相应的韧脆转变区间的预测曲线见图3。从图3(c)可发现,热影响区断裂韧度的分散性很大,高的特别高、低的则特别低,有较多的数据点落在5%和95%上下包络边界。这就是热影响区组织非均匀性导致断裂韧度性能非均匀的具体体现。为了获取热影响区中的薄弱环节,仅凭标准主曲线法很难实现。从分散性来看,母材和热影响区比焊缝金属具有更大的分散性。 表2同时给出了依据SINTAP法3个步骤的参考温度的预测。母材经过5次迭代后得到参考温度为-111.13 ℃,比标准主曲线法的升高了23.4%;焊缝金属经过1次迭代后为-69.35 ℃,和标准主曲线法保持一致;热影响区经过6次迭代后得到参考温度为-131.72 ℃,比标准主曲线法的升高了9.6%。SINTAP法和标准主曲线法的预测结果如图4所示。经比较可以看出,非均质的母材和热影响区的预测曲线在相应的主曲线法预测曲线的右下方。因此,针对分散区间较大的断裂韧度样本,本文所提到的方法可以适当降低韧性较好部分高断裂韧度的影响,从而获得偏保守的估计结果。在课题组之前积累的数据和研究中发现[9-10],非均质会导致断裂韧度的实际分布偏离基于主曲线法的三参数Weibull分布,且实际分布位于右侧,这意味着忽略非均匀性会导致危险的估计结果。 表3列出SINTAP法步骤2中的迭代结果,可以看出,非均匀性越大的材料迭代的次数就越多。对均质材料,SINTAP法和标准主曲线法的估计结果相当,如焊缝金属;对非均质材料,则会提高材料的参考温度,断裂韧度曲线将向高温区移动。 从宏观非均匀的筛查结果来看,母材被认为是非均质材料。然而,母材在断裂韧度试样取样时,严格控制了取样要求,所有试样的取样方向和相对位置保持一致(见图2)。为探讨非均匀筛查准则的可靠性,本文在第3.3节进一步进行讨论。 (a)母材 (b)焊缝 (c)热影响区 表3 SINTAP法步骤2迭代过程 为了讨论非均匀筛查准则的可靠性,收集了大量文献中的数据来检验公式(4),文献中的试样有清楚的取样位置和方向,运用非均匀性筛查准则得到每种材料的判定结果,如表4所示。文献[11]中测试了20个16MnR的断裂韧度数据,经分析是非均质的;文献[12]中测试了两种不同焊接工艺(仅焊剂选取不同)的16MnR焊缝断裂韧度,经判定一种是均质的、一种是非均质的;文献[13]中测试了大量A533B钢不同厚度的三点弯曲试样断裂韧度试验数据,测试温度都是-91 ℃,经非均匀筛查发现,厚度8 mm和31.8 mm的筛查结果是非均质的,而其他厚度是均质的。而事实是,这些不同厚度的三点弯曲试样都是取自同一批次的材料,非均质的筛查结果理应相同。因此可以看出,非均匀筛查准则可能会产生错误的结果,可能会将均质材料判定为非均质。对于统计分析和筛查,为了避免小样本的不确定性,ASTM E1921—2019建议筛查时应不少于20个数据。表4中文献[11-12]中的试验数据表明,即使到达20个数据点,依然很难准确判别材料是否非均匀。 表4 均匀性筛查统计 可见SINTAP法非均质筛查准则可能过于严格,会将一些均质数据集误判为非均质的。统计结果的准确性和数据数量直接相关,受限于材料实际情况,往往不允许开展大量的断裂韧度试验。那么SINTAP法到底需要几个数据点能够得到稳定可信的估计结果,以及非均质筛查的置信度和数据量之间的关系如何。受限于文章篇幅,关于这两点,笔者拟在下一篇文章中进一步讨论。 本文根据1999版欧洲结构完整性评价标准以及ASTM E1921—2019标准附录X5,介绍了用SINTAP判断一组断裂韧度试验数据是否非均质的步骤,用厚度60 mm的SA738Gr.B钢及其埋弧焊接头为研究对象,对母材、焊缝以及热影响区的断裂韧性进行了测试,用自编的SINTAP法执行程序统计并分析了断裂韧度的试验数据,给出3个区域的参考温度和转变区间内韧度分布。根据本文试验和相关文献的试验数据,得出了非均质筛查准则的应用范围。主要结论如下。 (1)标准主曲线法不适用于非均质材料,SINTAP法是一种解决非均质问题的有效手段。对非均质材料,会有效降低非均质的影响,产生适用于结构完整性评估的断裂韧度值;对均质材料,SINTAP法和标准主曲线法是等效的。 (2)SINTAP法中的非均质筛查准则比较严格,可能会产生错误的结果,有可能会将均质材料误判成非均质材料,使用时应谨慎对待。1.2 非均匀性筛查准则
2 试验研究
2.1 材料准备
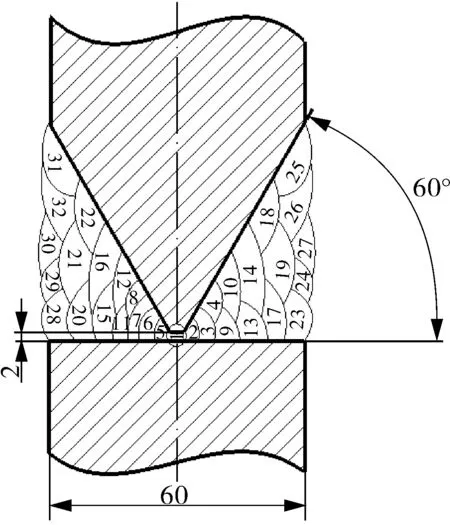
2.2 断裂韧度试验

3 结果与讨论
3.1 断裂韧度试验结果


3.2 SINTAP法预测结果


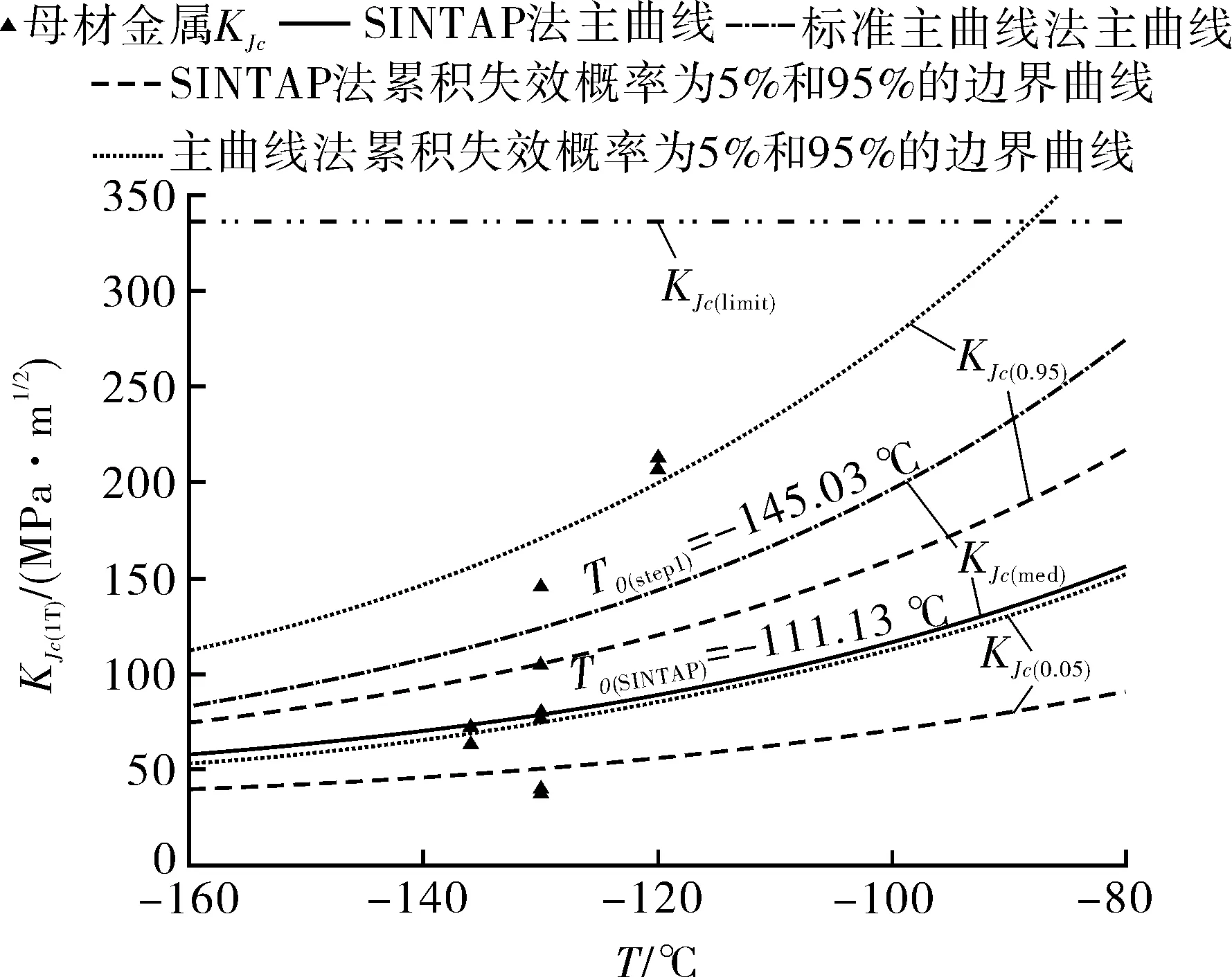



3.3 SINTAP法非均匀筛查可靠性讨论

4 结论

