基于健康监测的斜拉桥恒载索力提取与评估

宋晓东 崔珊珊 熊 文 吴 阅

(1东南大学交通学院, 南京 211189)(2安徽省交通控股集团有限公司, 合肥 230088)

结构健康监测(structural health monitoring, SHM)技术可以通过传感设备实时获取桥梁的结构响应，进而达到长期监测、检测结构损伤或退化的目的，因此在国内外大跨径桥梁上得到了广泛应用.由于SHM采集的桥梁响应包含了活载、温度、风等可变荷载产生的效应，采用SHM原始数据进行桥梁结构性能评估时缺乏统一的评估标准.因此，很多学者对基于SHM的荷载效应特征值抽取进行了研究.刘夏平等[1]采用最小二乘法建立了温度与挠度之间的关系，进而分离温度引起的挠度变化.Wang等[2]基于线性贝叶斯模型对温度引起的斜拉桥应变进行了预测分析.陈国良等[3]采用时间序列分析对斜拉桥的挠度与温度的相关性进行了研究.Wu等[4]基于多尺度模型对温度和车辆荷载引起的悬索桥应变成分进行了分离.Zhu等[5]采用移动主成分方法对桁梁桥的温度应变进行了抽取.刘纲[6]根据荷载效应的重现周期对温度、混凝土收缩徐变等效应信号进行了分离.

拉索索力是斜拉桥的重要指标之一，代表了斜拉桥的服役性能.剔除温度、活载等可变荷载效应后获得的恒载索力可以直观地反映整个结构的受力状态.任远等[7]以南京三桥封桥检测数据为基础，分析了索力与温度的相关性，进而对恒载索力的变化趋势进行了研究.Liu 等[8]采用统计分布拟合的方法得出索力的统计分布规律，并将最大概率密度的位置参数作为索力的恒载特征值.Ren等[9]提出了基于影响线和监测数据来获取恒载索力值的评估方法.上述研究对温度效应的研究较多，而对活载效应剔除方法的研究相对较少，缺乏对恒载索力特征值的抽取与评估的系统分析.

本文以某双塔双索面斜拉桥为研究背景，基于健康监测数据实现索力的高精度自动识别，并通过集合经验模态分解法(ensemble empirical mode decomposition, EEMD)来分离活载效应，通过数据拟合来识别温度效应，进而抽取恒载索力特征值，最终对结构的索力状态进行评估.

1 基于SHM的索力识别

1.1 背景工程

安庆长江公路大桥位于长江安庆河段，其结构型式为主跨510 m的双塔双索面斜拉桥，跨径布置为50 m+215 m+510 m+215 m+50 m，大桥主梁采用扁平流线形钢箱梁，桥宽30 m.箱梁沿桥纵向横隔板间距4.0 m.索塔采用钢筋混凝土分离上塔柱倒Y形索塔，总塔高184.781 m，拉索编号分别为A1～A16和J1～J16，其中A8、A16、J8和J16号上游和下游的拉索均安装了加速度传感器用于索力监测，其总体布置示意图如图1所示.

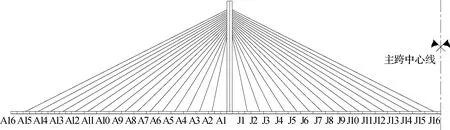
图1 安庆长江公路大桥拉索编号

1.2 基准频率自动识别

安庆长江大桥被SHM监控的斜拉索均为抗弯刚度可忽略不计的中长索，将加速度时程经过频谱分析后来确定拉索的自振频率，再基于自振频率与索力的关系确定索力.由于加速度传感器安装位置偏下，基频及其他低阶峰值能量较小，且第1阶频差与高阶频差相差较大，采用直接读取基频的方法会产生较大的误差,因此，分别采用平均频差法[10]和新基频法[11]来减少误差.经试算，对于安庆长江大桥，新基频法使得频谱图中个别尖峰的少量偏移对基频的识别结果影响较小，鲁棒性较强.因此本文采用新基频法进行分析，即先寻找频谱图中最高点对应的频率fp(峰值点频率)，再判断其对应的阶次n，进而获得拉索的基准频率.

为了判定阶次n，首先从频谱图中粗略估读出基频fe，选取频谱图中较为清晰可读的区间并识别出该区间中所有尖峰频率，然后将这些尖峰的平均频差作为基频的估算值.为了提高频谱峰值识别的可靠性，在此选择幅值不小于最高峰幅值20%的尖峰，认为其可读，并将以这些频率中最小、最大值为端点的区间定义为可读区间，如图2所示.

由于频谱图中存在大量的局部极值点，各尖峰的幅值大小差异较大且无定量规律，因此无法简单地根据极值点的判定方法来判读具有物理意义的尖峰，这为频率自动化识别带来了困难.为此，本文提出一种变间距栅格法用于尖峰的识别，具体为：将可读区间划分为形如栅格的若干等间距子区间，由于各尖峰近似等间距，若栅格间距接近尖峰间距(即频差)，则每个栅格中将有且仅有一个尖峰，且尖峰为该栅格中的最大值(见图3).由此，尖峰的搜索及定位问题转化为栅格合理间距di的确定问题，i为循环次数.

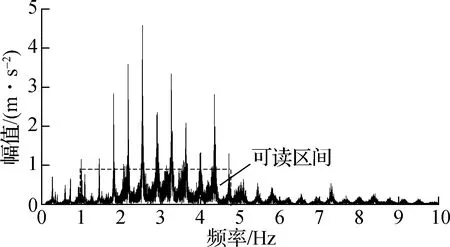
图2 可读区间的选取

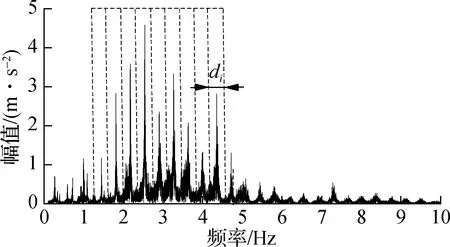
图3 栅格的选取

根据可读区间的定义，频谱图中最高峰位于可读区间中.设初始栅格间距为d0，为了后续方便搜索尖峰，将栅格的起点定在fp-0.5d0处，由起点从左向右划分栅格，直至最后一个栅格的右端点刚好不超出可读区间，这样可保证频谱中最高峰落在其所在栅格的中间位置；且确定栅格合理间距后，其余尖峰也将位于各自所在栅格的中间位置附近，如图3所示.若最高峰接近可读区间右端，可将频谱图水平翻转后进行上述过程，以保证栅格总长度尽可能覆盖可读区间的较大部分.

由此，设定栅格间距d0后，若存在一个栅格，其最大值位置接近该栅格的左右端点(例如，与栅格端点的距离小于栅格间距的20%)，则称该子区间为无效栅格.将无效栅格的数量与栅格总数的比值定义为无效栅格比例.若无效栅格比例不小于α(例如10%)，则认为该栅格间距d0不合理，此时按下式更新栅格间距为d1，重新判定其是否合理：

d1=d0+dΔ

(1)

式中，dΔ为每次循环时栅格间距增加的步长.由此循环，直至找到栅格合理间距di.根据实测频谱图的清晰与洁净程度，选择合适的α值，可避免将合理的di值误判为无效.

栅格间距确定后，即可在各栅格中搜索最大值及其对应频率，即找到了可读区间范围内的各阶尖峰频率；按从小到大顺序排列搜索到的尖峰频率，并计算相邻2个频率值的频差，获得频差向量F={F1,F2,…,Fr}，r为频差向量中的元素数量.考虑到传感器的位置不同，有可能发生个别阶频率不出现而造成频差计算误差较大的情况，在此采用3σ准则剔除偏离均值较大的频差，然后按下式计算即可得到基频的估值fe：

(2)

式中，j为频差向量F中的元素序号.得到基频估值fe后，即可用其判断最高峰频率fp对应的阶次n，进而根据两者的比值获得基准频率的准确计算值f.

由于监测数据时程存在野值，采用中位数绝对偏差法(MAD)进行了野值剔除，获得的基准频率如图4所示.当索力较小时，拉索的基频不等于频差，此时采用变间距栅格法只能获得高阶频率的频差，不能通过这种方法直接获得拉索的基准频率.

图4 J16号索的基频时程(2015年5—8月)

1.3 拉索张力计算

目前普遍采用简化张紧弦模型得到拉索张力与自振频率间的简化函数关系，简化的关系忽略了拉索抗弯刚度与垂度的影响，便于工程上的快速应用，但可能带来无法接受的误差.本文采用基于能量[12]并考虑拉索抗弯刚度与垂度效应情况下的索力计算方法，计算公式如下：

(3)

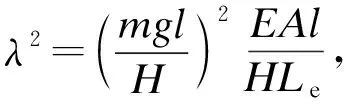
由于式(3)中存在超越方程，可能需要用迭代法计算索力T，λ2的计算也需要用到T值，因此首先估算T值，并由此大概确定λ2所处区间，进而选择公式计算索力.由于监测获得的索力时程存在噪声、缺失等问题，分别采用移动平均、分段三次Hermite插值法解决这些数据缺陷，提升数据的可读性，并与人工巡检数据相结合验证SHM数据均值的正确性，剔除了索力时程数据中由加速度传感器异常引起的异常数据，如图5所示.

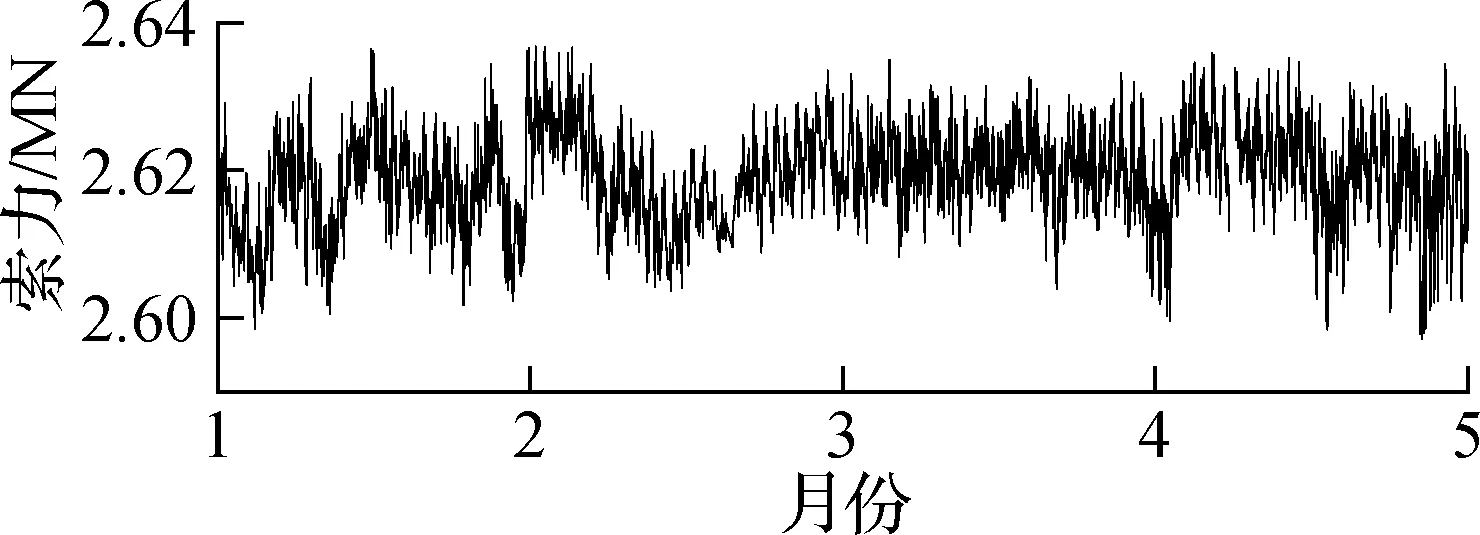
图5 J16号索的索力时程(2015年1—4月)

2 索力恒载特征值提取

2.1 活载效应剔除

据孙宗光等[13]和刘小玲[14]的研究，索力受温度的影响最大，远远大于其他因素的影响，车辆荷载的影响为短时的突变，因此本文仅进行活载和温度效应的剔除.首先，选用集合经验模态分解法(EEMD)[15]进行活载效应剔除，将索力原始信号分解为若干阶本征模态函数(IMF)及残差(residual)，如图6所示.对于图6这段索力时程，EEMD将原信号分解为8阶IMF及1个残差.由结果可知，EEMD分解所得各阶IMF，阶数越低越趋向于高频信号，阶数越高越趋向于低频信号，这也与EEMD逐阶分解的特性相吻合.得到各阶IMF后，接下来需要考虑的是剔除哪些IMF以达到剔除活载效应的目的.

当忽略风荷载效应的影响时，剔除活载效应的索力时程只含温度与恒载成分，即相对低频缓变的成分.因此应从残差开始，从高阶向低阶选取IMF，并确定IMF阶数的阈值[16].此外，索力温度效应的变化与温度的变化存在约1 h的时滞，但二者的变化存在周期性，相关性较强[13].因此考虑计算SHM温度数据、各阶IMF的频谱，找到与温度变化频率最接近的IMF(频谱图中峰值频率相等)，将该IMF、更高阶的所有IMF以及残差求和，即可得到仅含有温度效应的索力时程.

提取J8号索(下游)附近的温度传感器2015—2016年的监测数据，并去除噪声、离群值及小段缺失后进行频谱分析，结果如图7所示.由图可知，SHM温度数据最主要的频率成分为11.64 μHz，而11.64 μHz对应的周期为0.994 d.因此，温度变化的主要周期成分为1 d，各阶IMF的FFT频谱图如图8所示.由图可知，第1阶和第2阶IMF频谱中没有明显峰值，表明IMF1与IMF2为与白噪声类似的随机过程，与活载效应的特性相符；第3阶和第4阶也没有明显的峰值，但是峰值较高的频率区域不断缩小；第5阶的主要频率成分为11.65 μHz，与温度变化频率非常接近；第5阶及更高阶IMF的频率成分均小于11.65 μHz.由于温度效应和活载效应是引起索力波动的2个重要因素，而车辆荷载的激励频率更高，因此将11.65 μHz作为温度效应和活载效应的分解，即将高于这一频率的本征模态值(IMF1～IMF4)归于活载效应引起的波动.根据上述结果及前述分析，将IMF5～IMF8及残差相加，并将此作为剔除活载效应后(仅含温度效应)的索力时程，如图9所示.

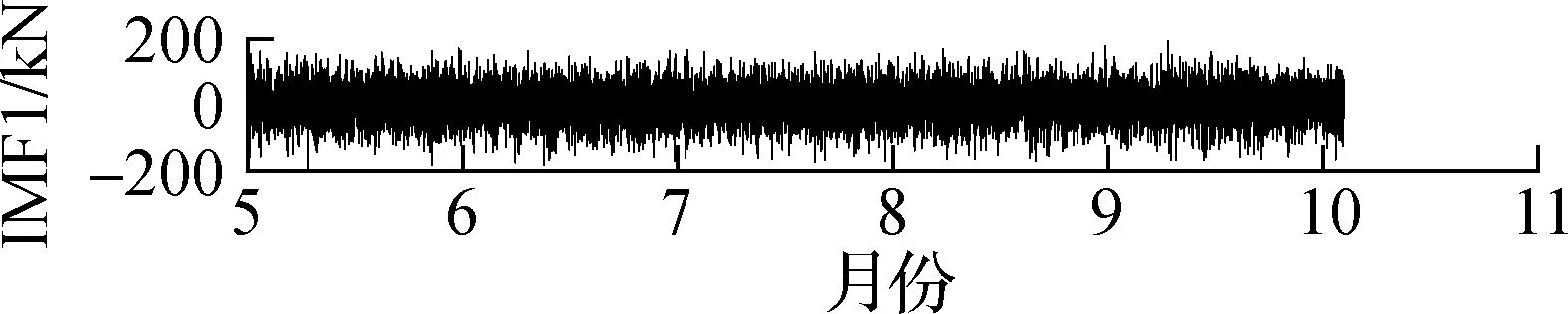
(a) IMF1

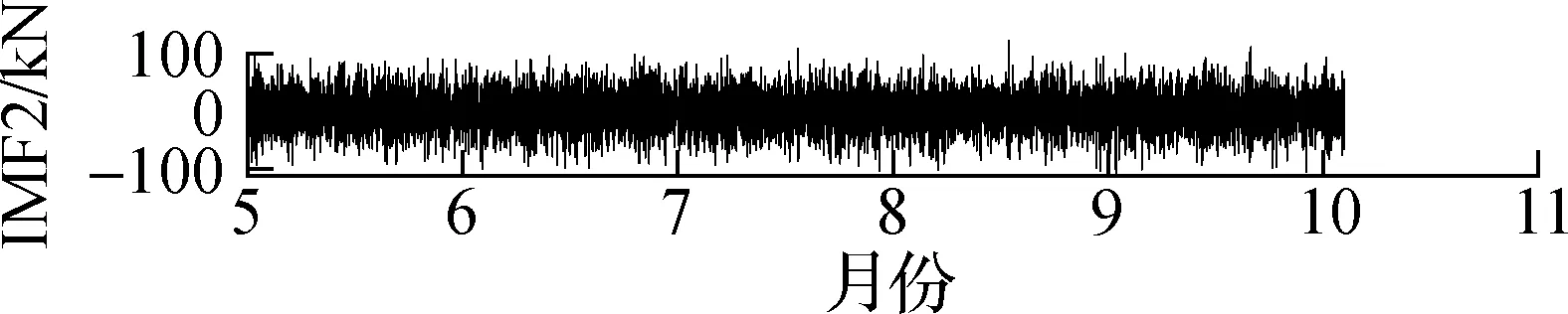
(b) IMF2

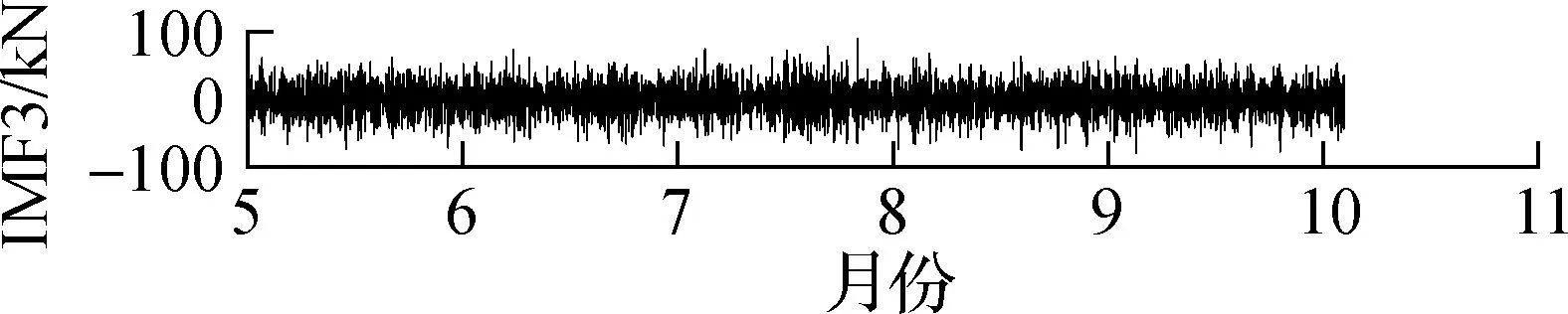
(c) IMF3

(d) IMF4

(e) IMF5

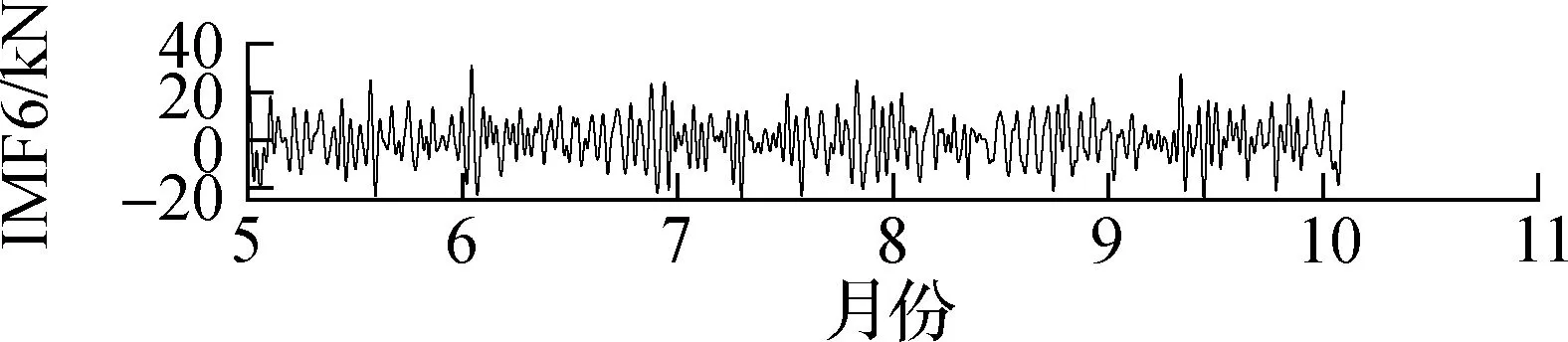
(f) IMF6

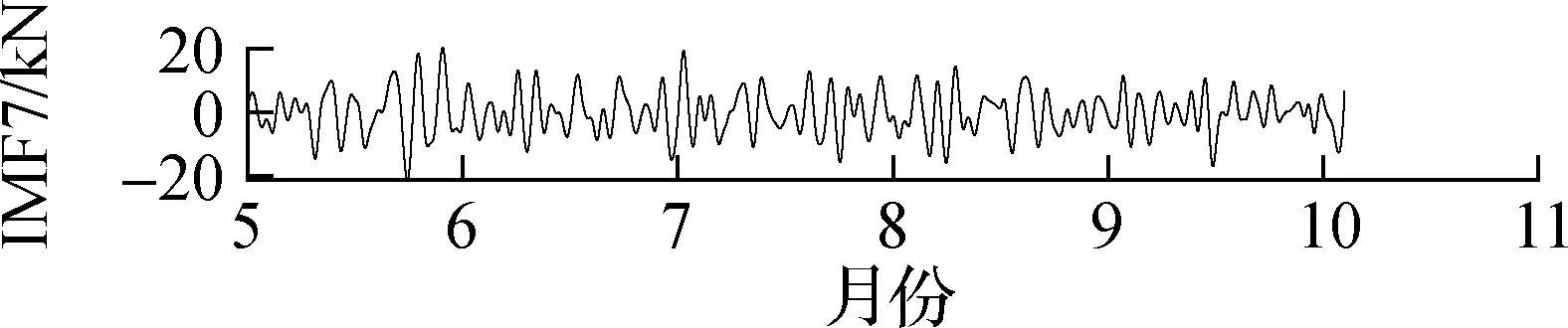
(g) IMF7

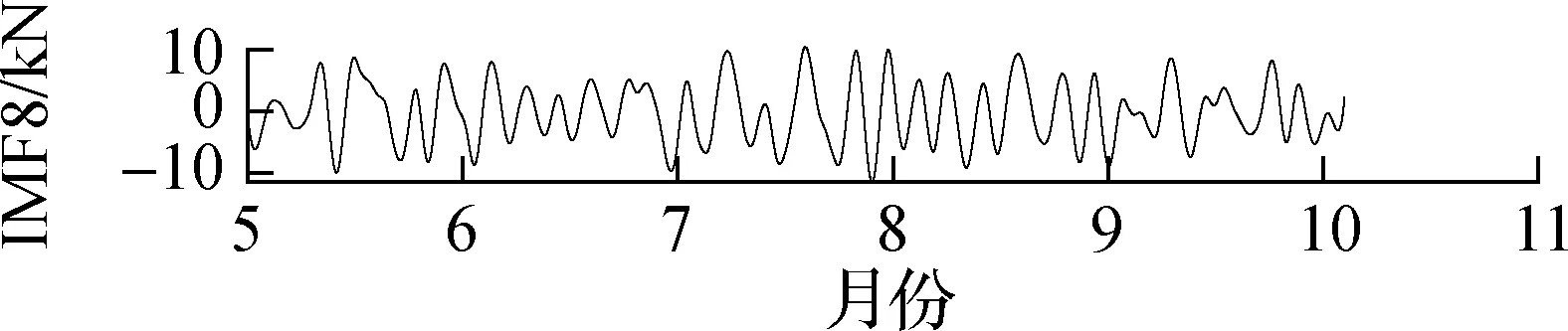
(h) IMF8

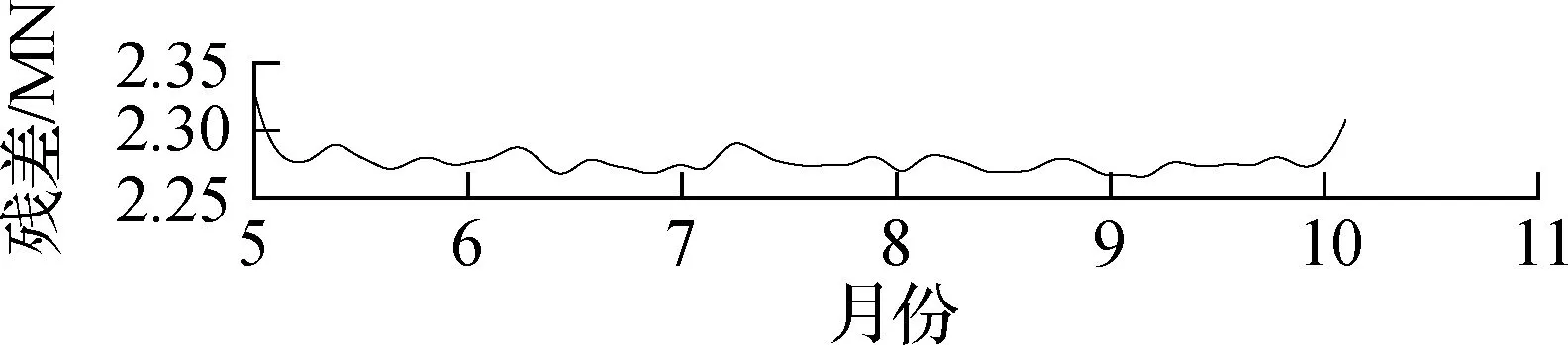
(i) 残差

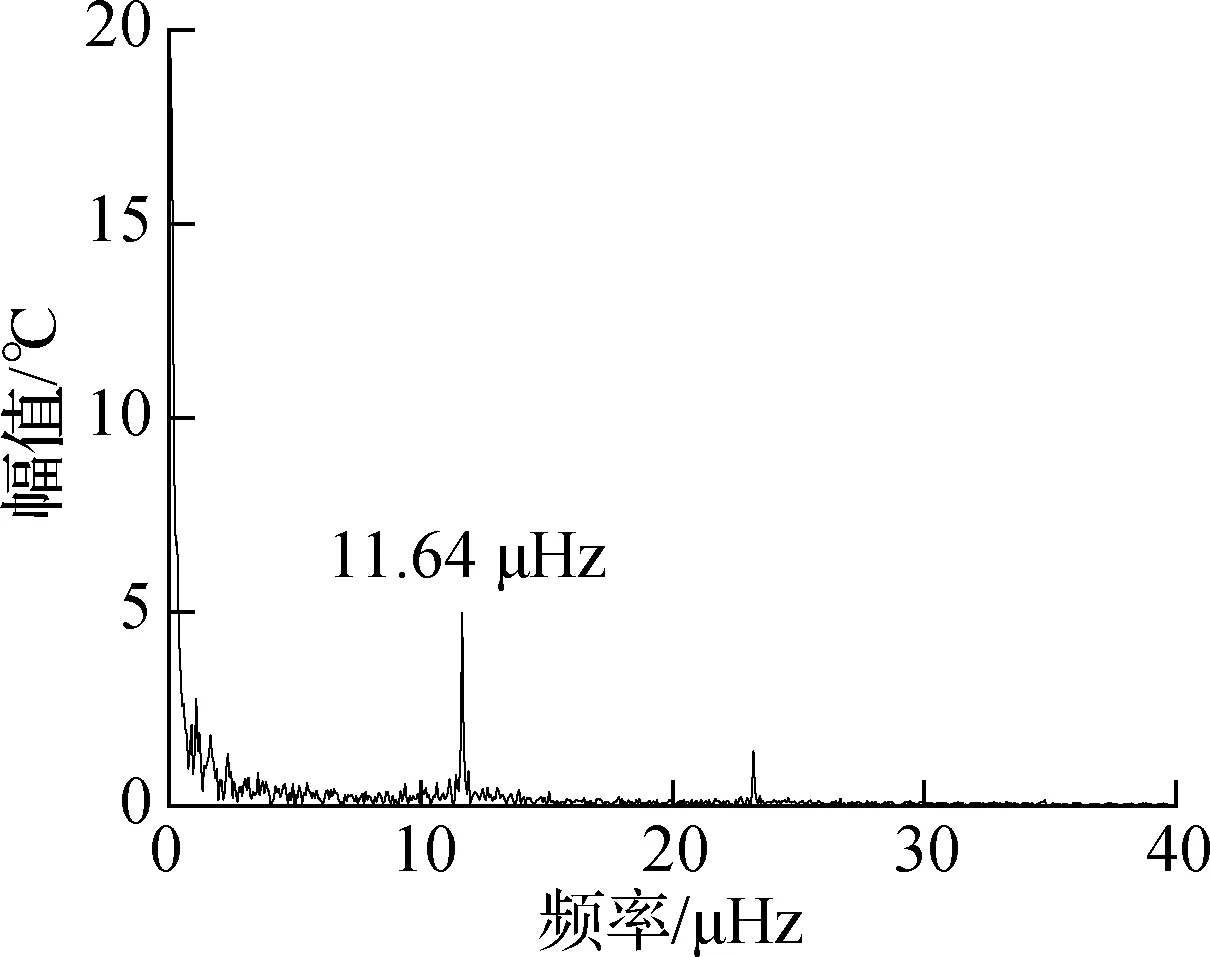
图7 J8号索附近的温度频谱(2015—2016年)

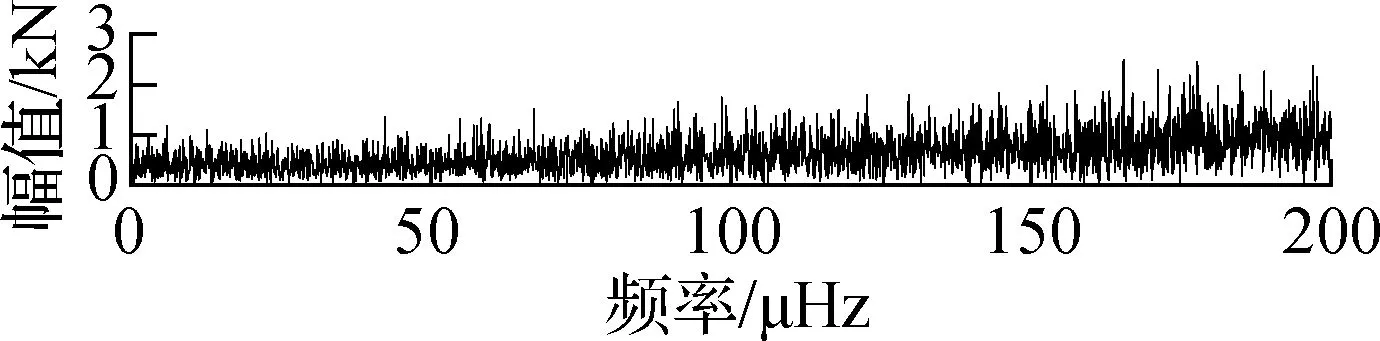
(a) IMF1

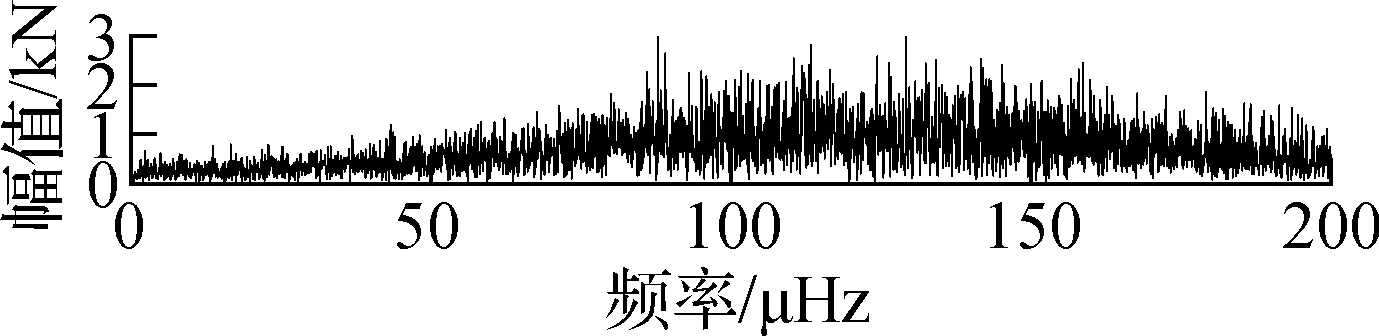
(b) IMF2

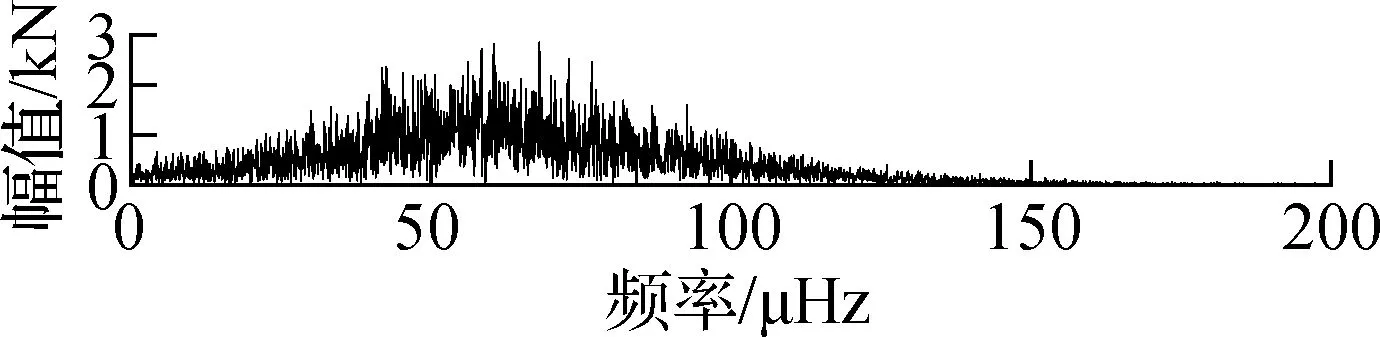
(c) IMF3

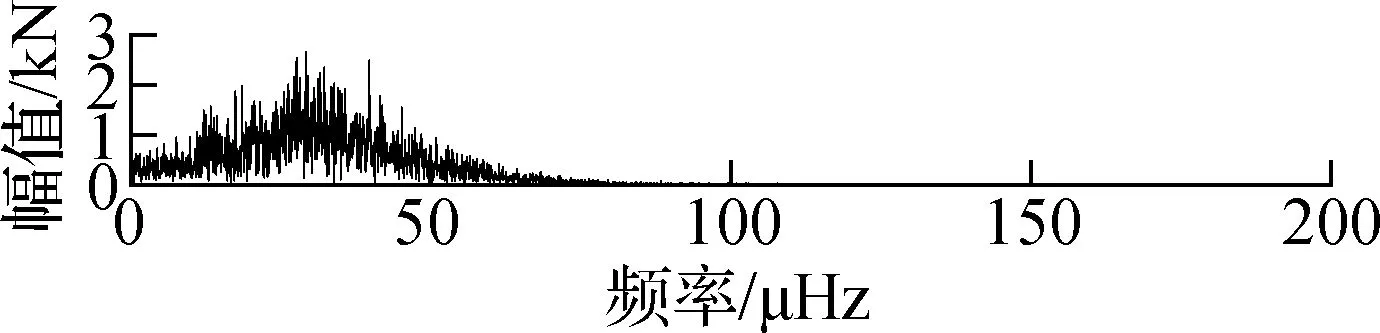
(d) IMF4

(e) IMF5

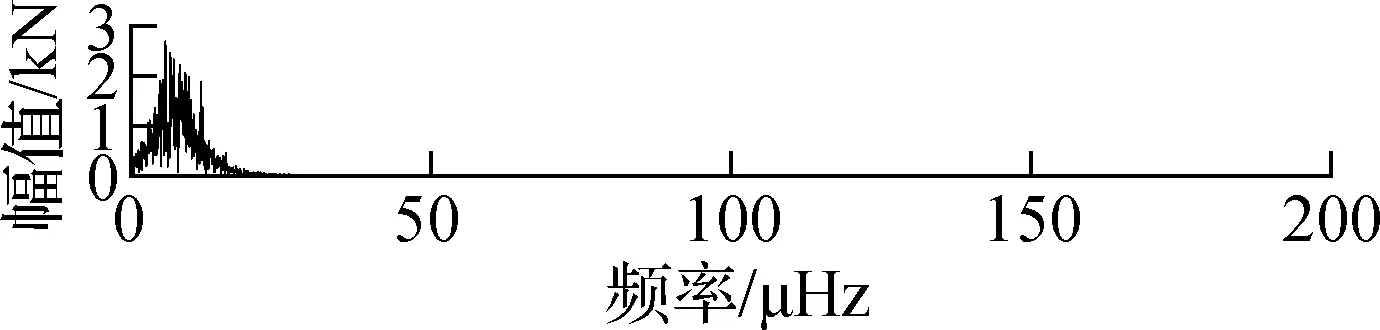
(f) IMF6

(g) IMF7

(h) IMF8

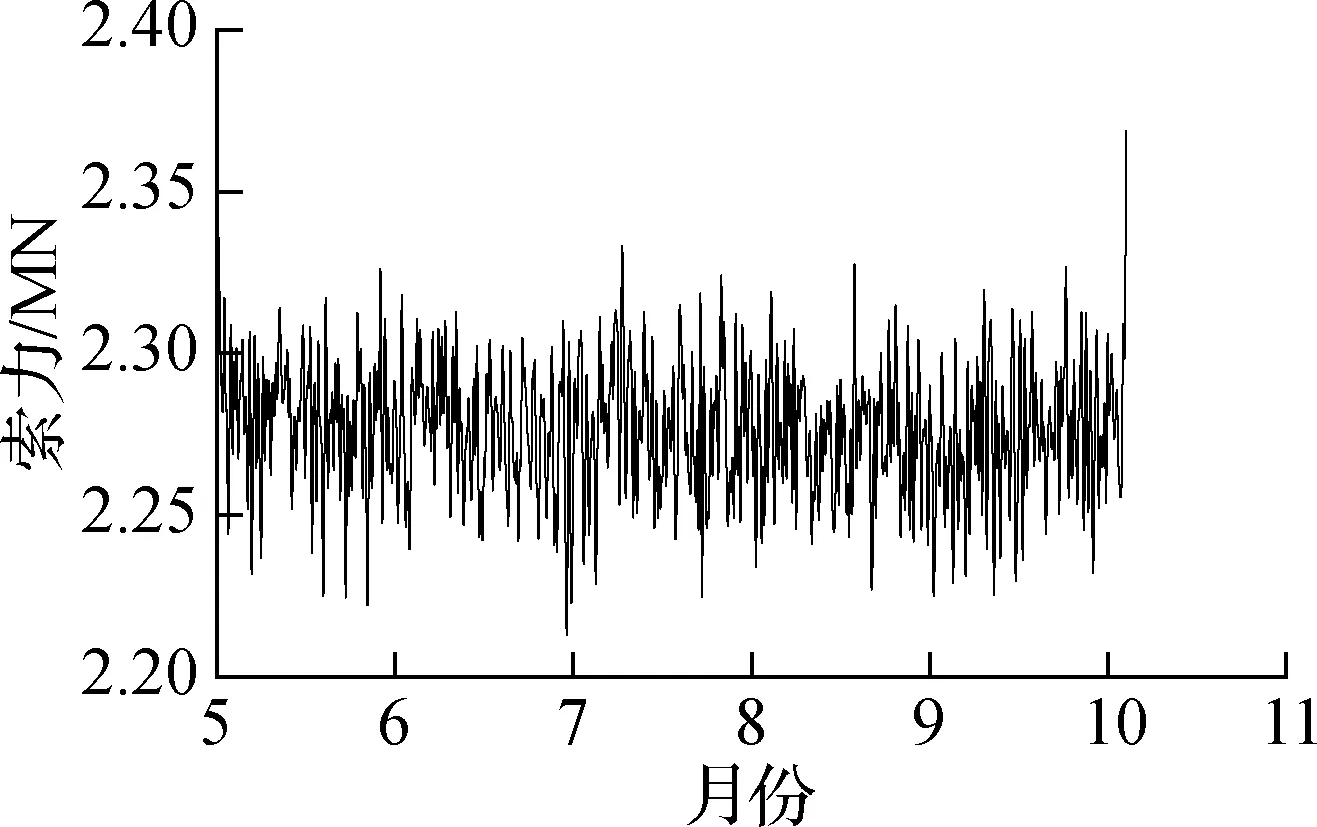
图9 剔除活载效应的J8索力时程(2015年5—9月)

2.2 温度效应剔除

经过活载剔除后得到的索力时程还包含温度效应，将其剔除即可获得反映结构自身特性的恒载特征值.桥梁结构所受温度作用分为季节性温度作用与日照温度作用，前者的效应为结构整体升降温，后者的效应为结构不同部位产生温差.研究表明[13]，索力中的季节性温度效应与温度的关系近似呈线性，找出二者的关系相对容易；而日照温度效应与温度的关系比较复杂.考虑到夜间日照温度效应小，且本研究的目的为长期监测而不必覆盖每天的全部时段，因此取每日00:00—05:00的索力与温度数据进行分析，以剔除日照温差效应.

取J8号索(下游)索力时程与温度传感器2015—2016年每日00:00—05:00的数据进行拟合分析，结果如图10所示.

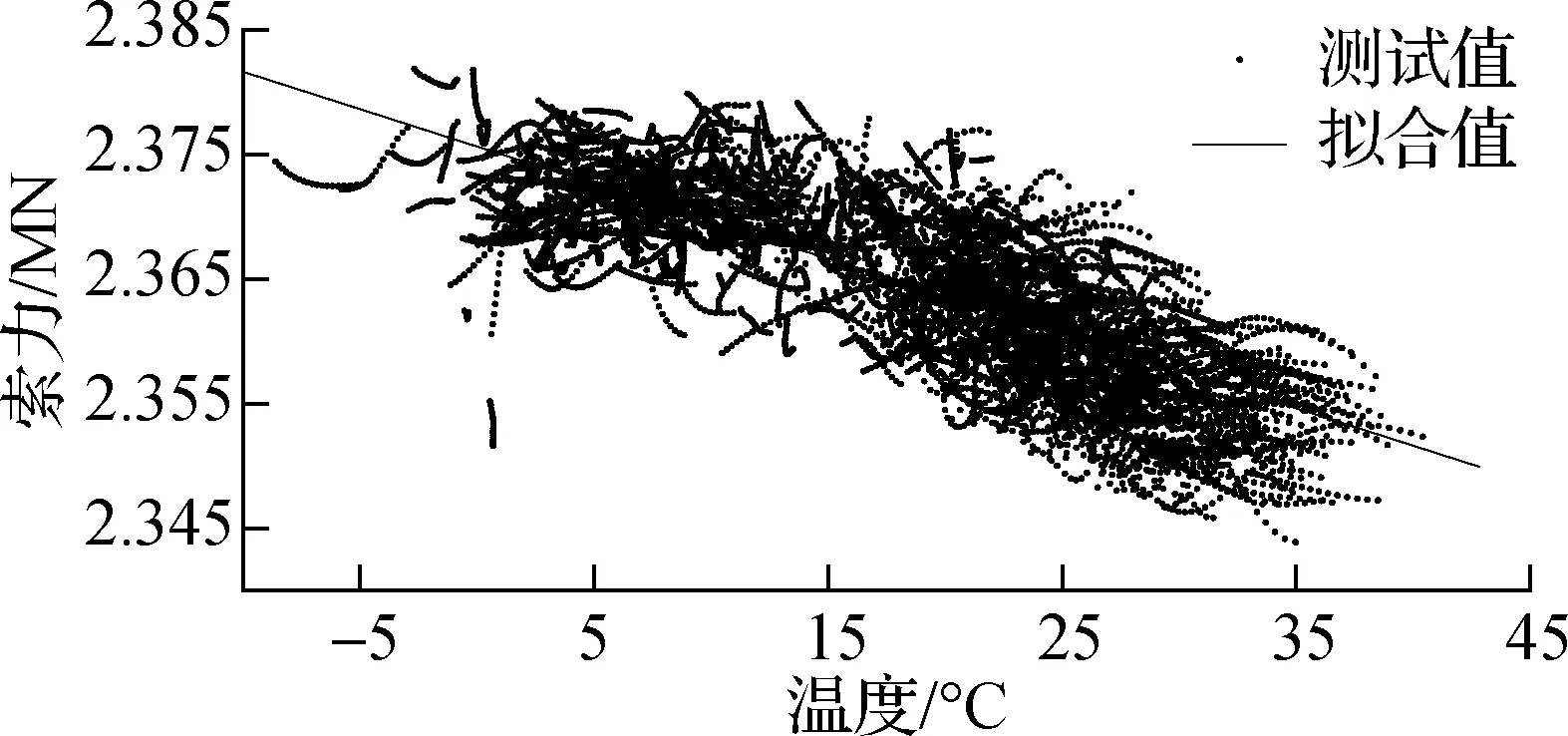
图10 J8号索温度与索力数据拟合(2015—2016年)

根据拟合结果，将J8号索(下游)2015—2016年每日00:00—05:00的索力时程统一至20 ℃(其他温度亦可)，即得到剔除温度效应的索力时程，如图11所示.

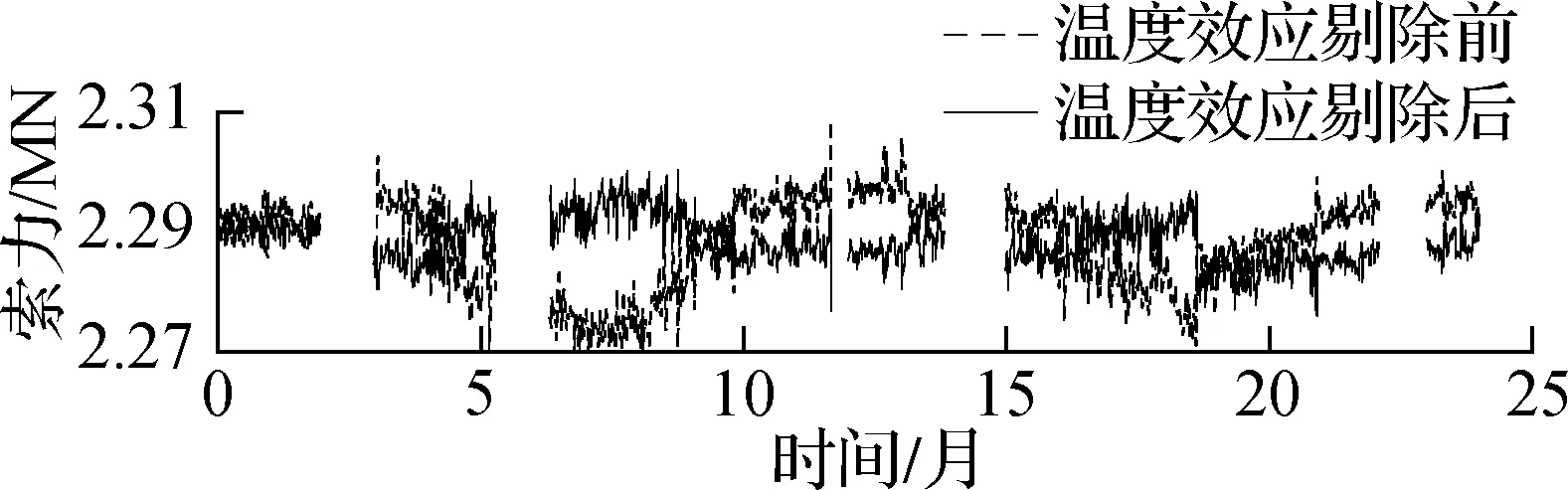
图11 J8恒载索力时程(2015—2016年)

3 拉索状态评估

3.1 评分标准

可以认为，设计阶段提出的设计索力，是最有利于保持整座结构健康的索力状态.因此，若拉索的张力均接近于设计索力，则表明结构状况更加健康；反之，若存在某根或某些斜拉索，其张力相对于设计索力过大或过小，则表明全桥索力状态已偏离设计索力，结构健康状况存在问题.同时，索力大小不能超过其材料的承受能力.

根据上述定性分析，斜拉索的张力属于适度指标模型，即存在一个标准状态，越接近标准值越好.根据这样的原则，若索力等于标准状态，则可评为满分；若索力偏离标准状态达到一定程度，则评为零分.同时需要考虑索力是否接近拉索材料承受能力的上限，在拉索中拉应力接近材料强度时已极度不安全，也应判为零分.根据熊文等[17]的研究，将索力偏离标准状态的程度用索力变化的百分比量化，并以给定的百分比作为零分标准.综合考虑了适度指标模型以及材料强度2方面，将索力偏离标准状态40%定为零分标准，中间的状态按照适度指标模型进行曲线插值，公式如下：

式中，tk为拉索k的实测值；tk0为拉索k的标准状态值；tku=0.6tk0；tkv=1.4tk0；A为评估值取值上限，取100；B为形状参数，取-0.5.

根据式(4)获得索力评价值后，将其分为5个评定等级：81～100分为1级(良好)，61～80分为2级(较好)，41～60分为3级(较差)，21～40分为4级(差)，0～20分为5级(危险).得到各拉索评价值后，进而判断是否需要采取相应的管养措施.

3.2 评估结果

基于SHM数据，可以实时得到索力值并进行动态评估.在此，每隔2 min当有新的索力值被测出，随即进行分析计算并与评分标准进行对照(简称实时评分)，若评定标度为3级或更差，则给出预警信号.同时，对每个月的评价值序列求取均值、标准差以及95%置信区间(简称月度评分)，由此宏观分析该月索力的分布是否良好，适合用于长期趋势性的评估与决策.

图12为J8号索(下游)2015—2016年的实时评分序列.图13为J8号索(下游)2015—2016年的月度评分序列.由评估结果可知，拉索在2015—2016年得分均为95分以上，属良好状态，并不存在明显的索力变化情况.本文仅针对索力进行索状态评估，不能直接反映索的腐蚀等其他因素的影响，仅代表索力这一项指标的评估结果.

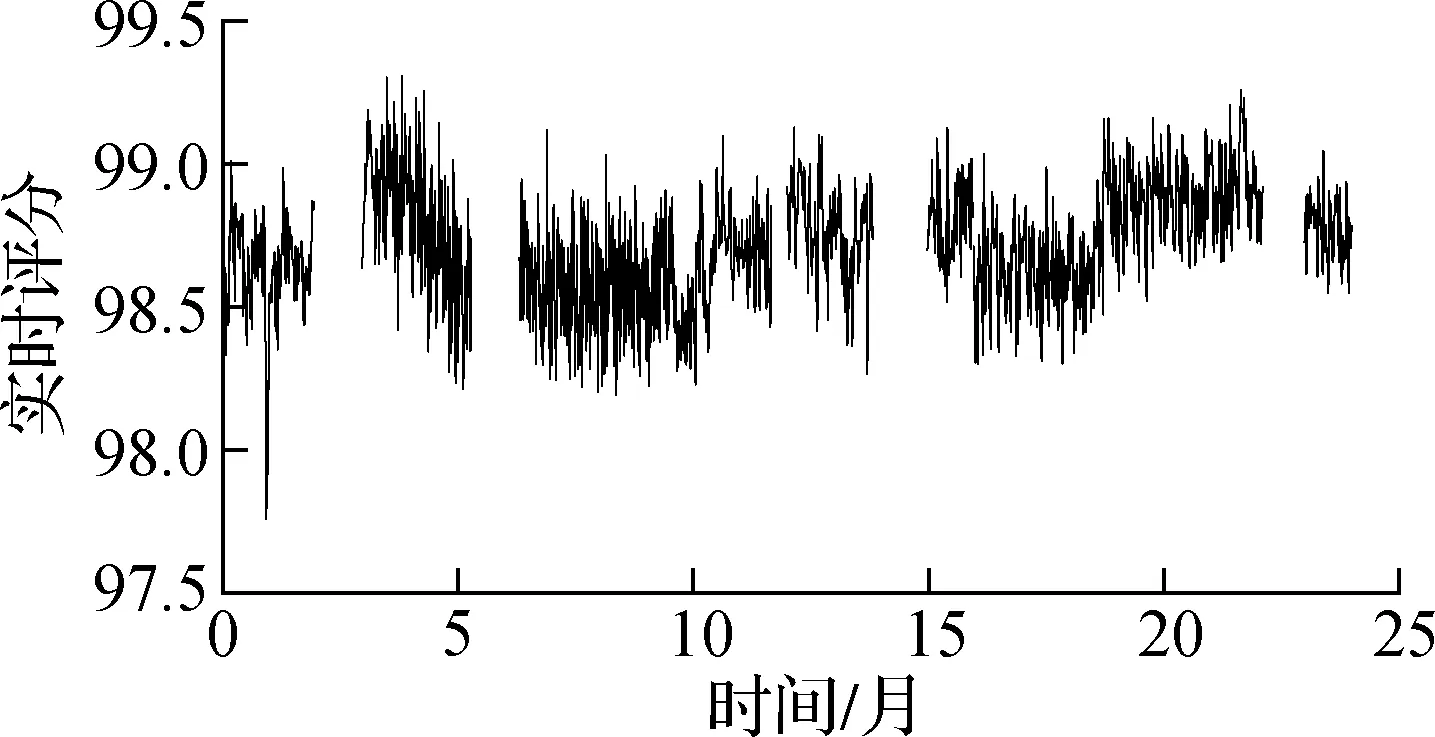
图12 J8索力实时评分序列(2015—2016年)

(a) 均值

(b) 标准差

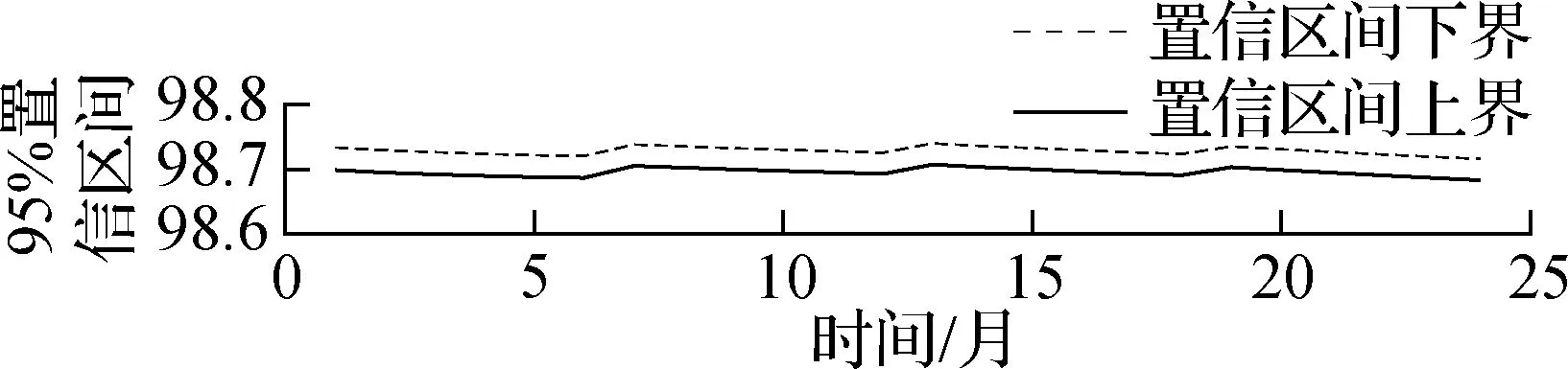
(c) 95%置信区间

4 结论

1) 基于健康监测数据和变间距栅格法可以快速获得拉索的索力，经过与人工巡检数据的互校融合可以及时发现加速度传感器的异常与问题，提高SHM数据用于桥梁分析评估的有效性.

2) 基于集合经验模态分解方法，将运营索力分解为8阶本征模态函数，结合温度变化规律相关性分析可以有效剔除活载引起的索力.温度的峰值频率为11.64 μHz，对应的周期为1 d.温度与索力存在较明显的线性关系，通过拟合函数可以有效剔除温度效应.

3) 根据固定的索力变化百分比定义满分与零分状态，兼顾拉索的极限承载能力以及拉索变化对结构的影响，采用适度指标模型进行曲线插值，可快速实现索力的实时评分与月度评分，以满足SHM系统实时监测与月度总结2方面的需求.