非接触桩箱复合基础竖向承载特性分析

栾 阳 杨 阳 戴国亮 龚维明 贾其军

(1东南大学土木工程学院，南京 210096)(2东南大学混凝土及预应力混凝土结构教育部重点实验室，南京 210096)(3中国路桥工程有限责任公司，北京 100011)

目前，我国桥梁建设正主攻跨越海峡连岛工程和西部大开发跨峡谷沟壑工程，这些桥梁工程多为重大发展战略规划的先导性工程，无论在政治上、还是经济上都具有举足轻重的地位.但这些重大工程多位于地震频繁且强烈的发震断裂带，作为生命线工程的大跨桥梁抗震问题应高度重视.

传统的桥梁隔震是通过设置减震装置，将上部结构体系与下部结构隔离开来，以减少地震传递到结构体系的能量[1].然而，大跨桥梁一般基础规模及基础刚度极大，上部结构与下部结构之间的减震装置减震效果有限，在强震条件下刚度巨大的基础面临着破坏的风险.希腊里约-安蒂里奥大桥(Rion-Antirion Bridge)为解决大跨桥梁抗震问题，采用了一种由沉箱、垫层、桩复合地基组合而成的非接触桩箱复合基础[2-3].垫层置于沉箱与桩复合地基之间，既可均化上部荷载、减小不均匀沉降，同时还具有隔震的功能.目前，已经建好的希腊里约安蒂里奥大桥和土耳其的伊兹米特海湾大桥(Izmit Bay Bridge)[4-5]，在建的丹麦新斯托海峡大桥(New Storstrøm Bridge)[6]以及土耳其的恰纳卡莱大桥(Çanakkale Bridge)[7]，也采用了这种形式的基础作为桥梁的主塔基础.非接触桩箱复合基础已有20年历史，但是过往针对非接触桩箱复合基础的研究均局限于对应桥梁基础设计的校验[8-11]，承载机理及沉降规律的研究较少.

非接触桩箱复合基础在结构上类似刚性桩复合地基.刚性桩复合地基已得到了广泛应用和研究[12-13].相较于传统的刚性桩复合地基，非接触桩箱复合基础所受竖向荷载巨大，垫层材料粒径越大(10～80 mm)，垫层铺设厚度越厚(3 m)，加固用的桩体多为钢管桩，且上部沉箱为裸置.在具体结构上，非接触桩箱复合基础与传统刚性桩复合地基有很大的不同，现有刚性桩复合地基的设计理论不能直接应用于非接触桩箱复合基础.因此，有必要对非接触桩箱复合基础进行进一步的研究.

本文首先进行了非接触桩箱复合基础竖向承载力室内模型试验，分析了非接触桩箱复合基础竖向承载性能及沉降规律.然后，采用颗粒流软件与有限差分软件，建立非接触桩箱复合基础离散-有限差分多尺度耦合分析模型，将模型计算结果与室内试验结果进行对比，验证模型的可靠性.最后，从宏观和细观多尺度分析了非接触桩箱复合基础的力学行为，为非接触桩箱复合基础研究提供参考.

1 试验

1.1 试验模型

以琼州海峡跨海大桥的主塔基础为依托，采用1∶100相似比，设计非接触桩箱复合基础室内模型试验，试验模型见图1.沉箱模型为106 cm×70 cm×56 cm的圆端形沉箱，由厚度为3 cm的Q235钢板焊接而成，内设加筋肋保证刚度.桩模型为外径43 mm、壁厚3 mm、长40 cm的钢管桩.沉箱下部共均匀布置36根模型桩，桩间距为3倍桩径.垫层采用粒径为2～5 mm的角砾，地基土采用中砂，材料性质见表1.

(a) 模型正视图

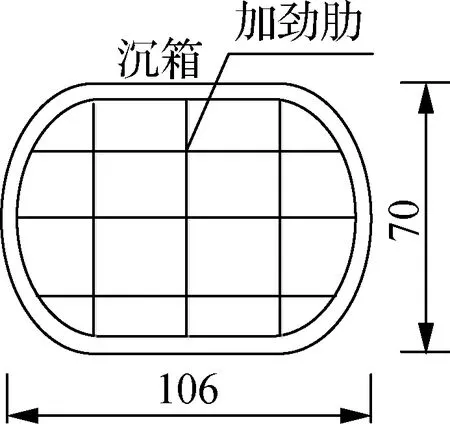
(c) 模型俯视图

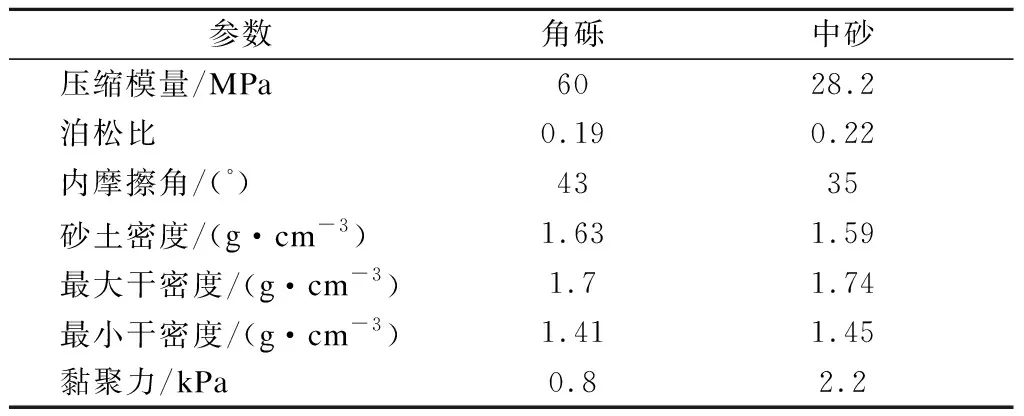
表1 垫层和地基土基本参数

1.2 传感器布置

沿桩身布置应变片，测量桩在竖向荷载作用下的桩身应变，以计算桩身轴力.应变片粘贴在桩内侧，单根桩应变传感器布置见图2(a)，被测桩包括图2(b)中的桩A、桩B、桩C和桩D.振弦式微型土压力盒安装在垫层底部，测量垫层底部土压力值，得到土压力分布情况，土压力盒的测点布置见图2(c).采用应变式位移传感器测量基础沉降，加载前将位移传感器固定在可移动的基准架上，位移传感器测点布置见图2(d).

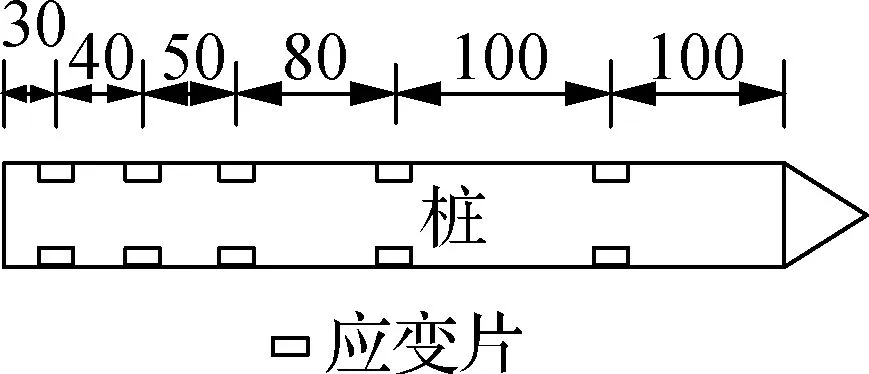
(a) 应变片布置

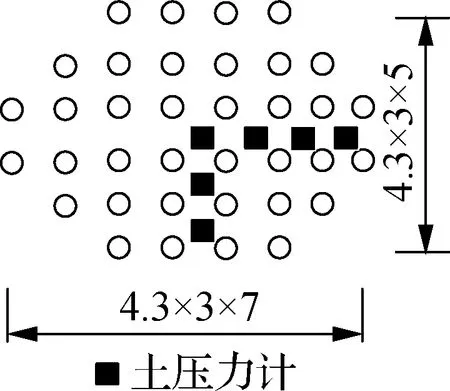
(c) 土压力计布置

1.3 试验方案

为研究有、无垫层及垫层厚度对非接触桩箱复合基础竖向承载性能及沉降的影响，设计了4组试验(见表2)，其中垫层厚度是指桩顶到沉箱底面之间距离.

表2 试验模型分组

试验采用分级加载，每级荷载分别为75、150、225、300、375、450、525、600 kN.每级荷载加载后维持1 h，并分别于5、10、15、30、45、60 min时采集一次数据，若位移变化量小于0.1 mm，表示竖向位移稳定，进入下一级加载.当沉降急剧增大、压力-沉降曲线出现陡降段时，或曲线为缓变型、累计沉降量超过40 mm时，终止加载.

2 试验结果与分析

2.1 沉箱的荷载-位移曲线

图3为不同厚度垫层模型沉箱的荷载-位移曲线.由图可知，荷载位移曲线为缓降形.相同荷载条件下，垫层越厚，沉箱沉降越大.究其原因在于，垫层越厚，竖向荷载条件下垫层压缩量越大，由垫层压缩造成的沉箱沉降也越大；垫层越薄，其对桩、土的变形协调能力越弱，大部分荷载由桩承担，因此桩复合地基整体沉降减小.

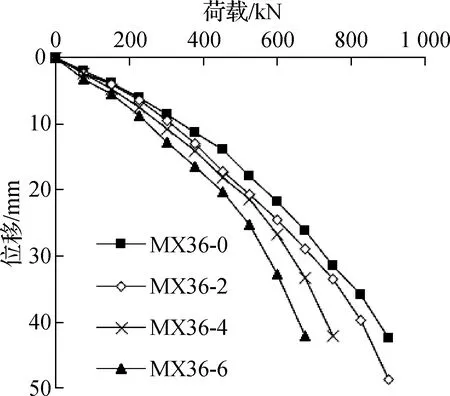
图3 不同厚度垫层模型沉箱荷载-位移曲线

2.2 桩身受力

图4给出了各级荷载条件下各模型中心桩桩A的桩身最大轴力.由图可知，各模型中桩身最大轴力随荷载增加而线性增加，且模型MX36-0与MX36-2的增加速度更快.总体而言，桩身受力与上部荷载近似为线性关系，因此取600 kN荷载条件下各桩身受力做进一步分析.

图4 桩A的桩身最大轴力随荷载变化曲线

图5为600 kN荷载条件下，不同厚度垫层模型中心桩桩A的轴力及摩阻力分布曲线.由图可知，无垫层模型桩基的桩身轴力沿桩深递减，仅存在正摩阻力；有垫层复合桩基的桩身轴力沿桩深先增大后减小，且在承载过程中桩顶刺入垫层，垫层颗粒流动补偿使得桩土保持紧密接触，土体沉降大于桩体沉降，桩顶部分存在负摩阻力.由图5(b)还可知，随着垫层厚度的增加，桩身负摩阻力部分增大.当垫层厚度为2、4、6 cm时，负摩阻区域分别为桩长的0.20、0.31、0.43倍.随着垫层厚度的增加，同级荷载作用下桩身同一位置处的负摩阻力增大.

图6为600 kN荷载条件下模型MX36-4各桩的轴力及摩阻力分布曲线.由图可知，同一模型中桩身受力相似，中性点高度基本一致，边桩轴力大于中心桩轴力.

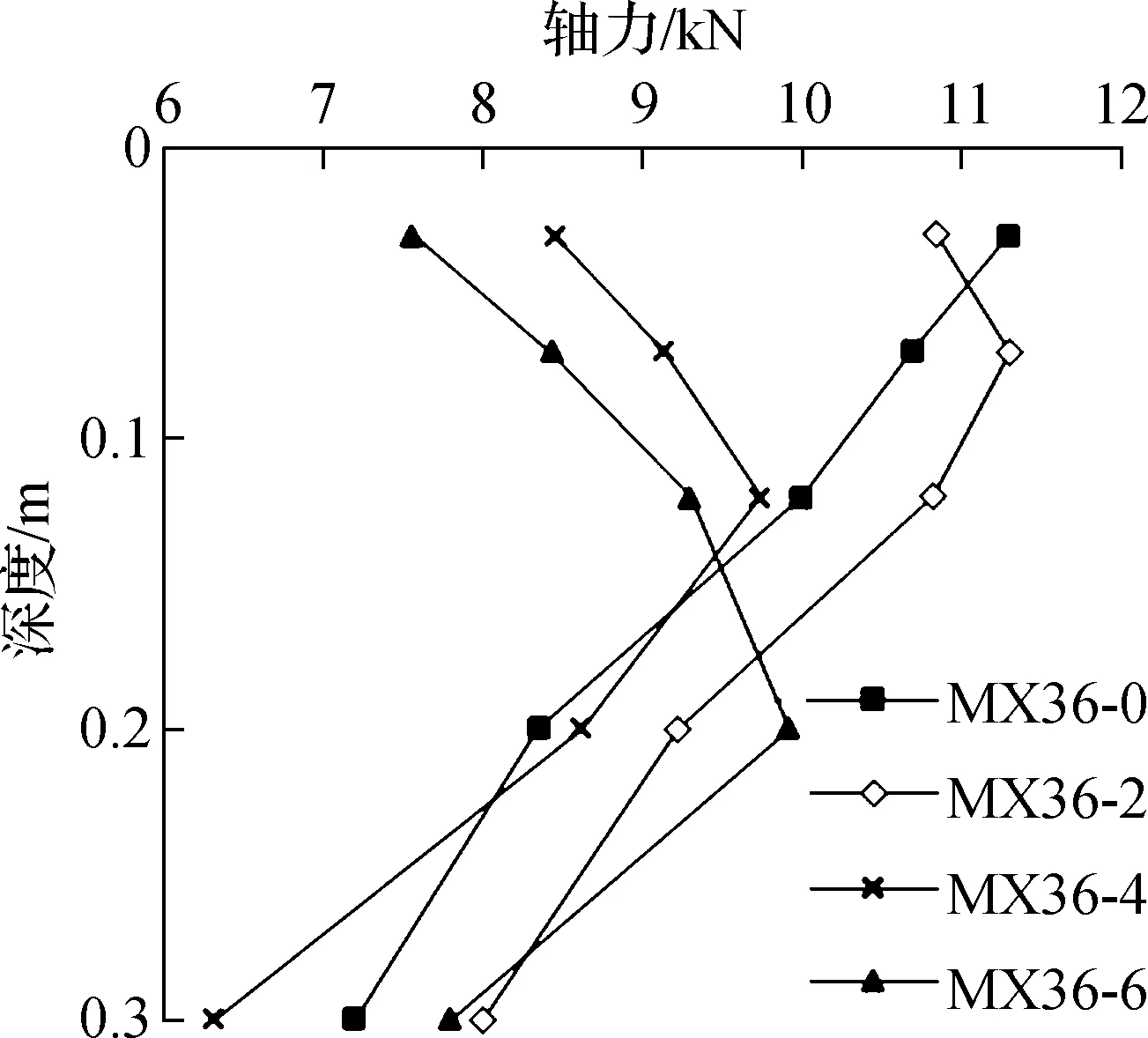
(a) 轴力

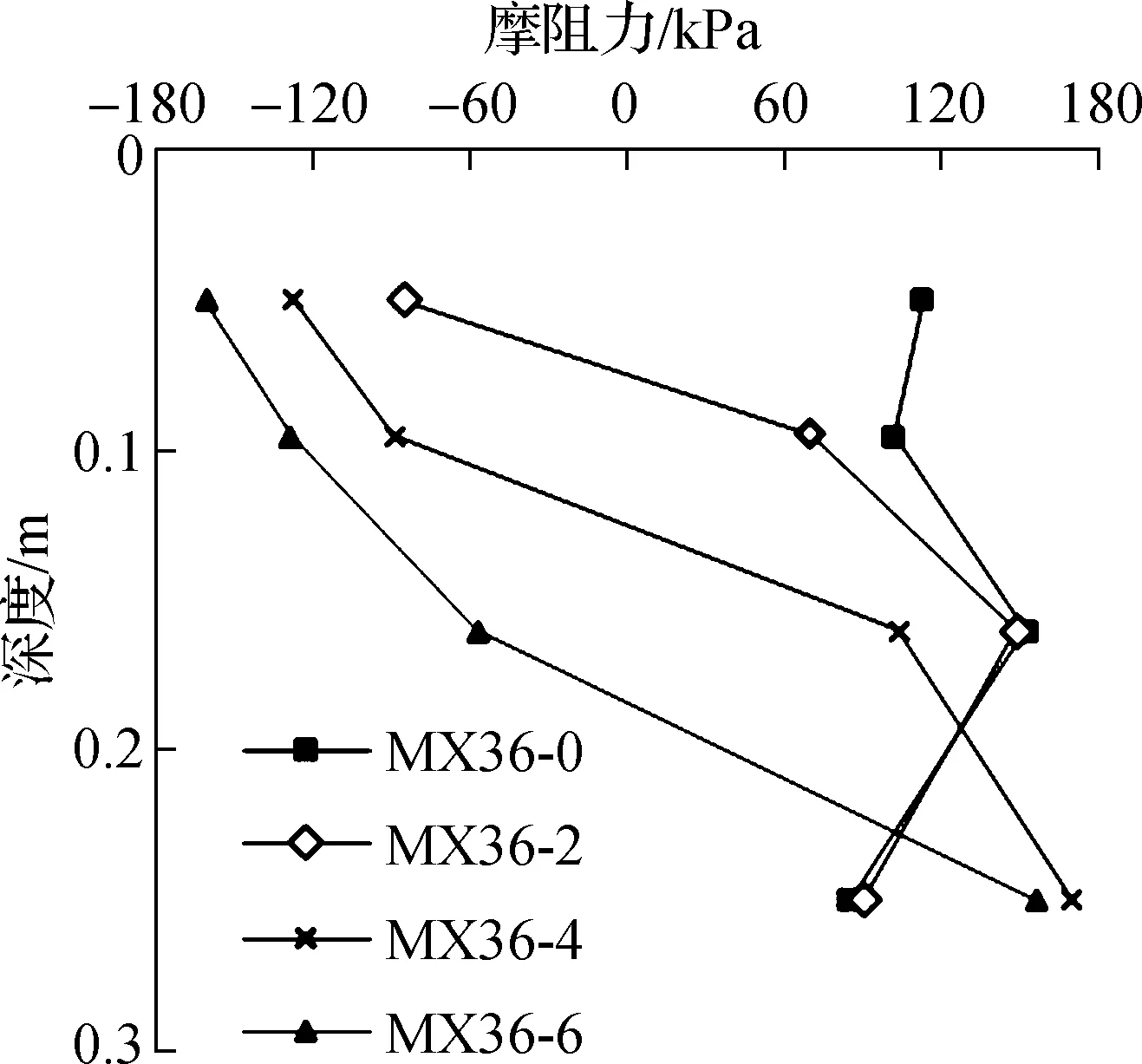
(b) 摩阻力

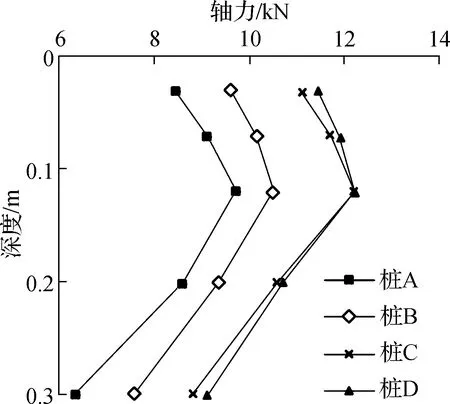
(a) 轴力

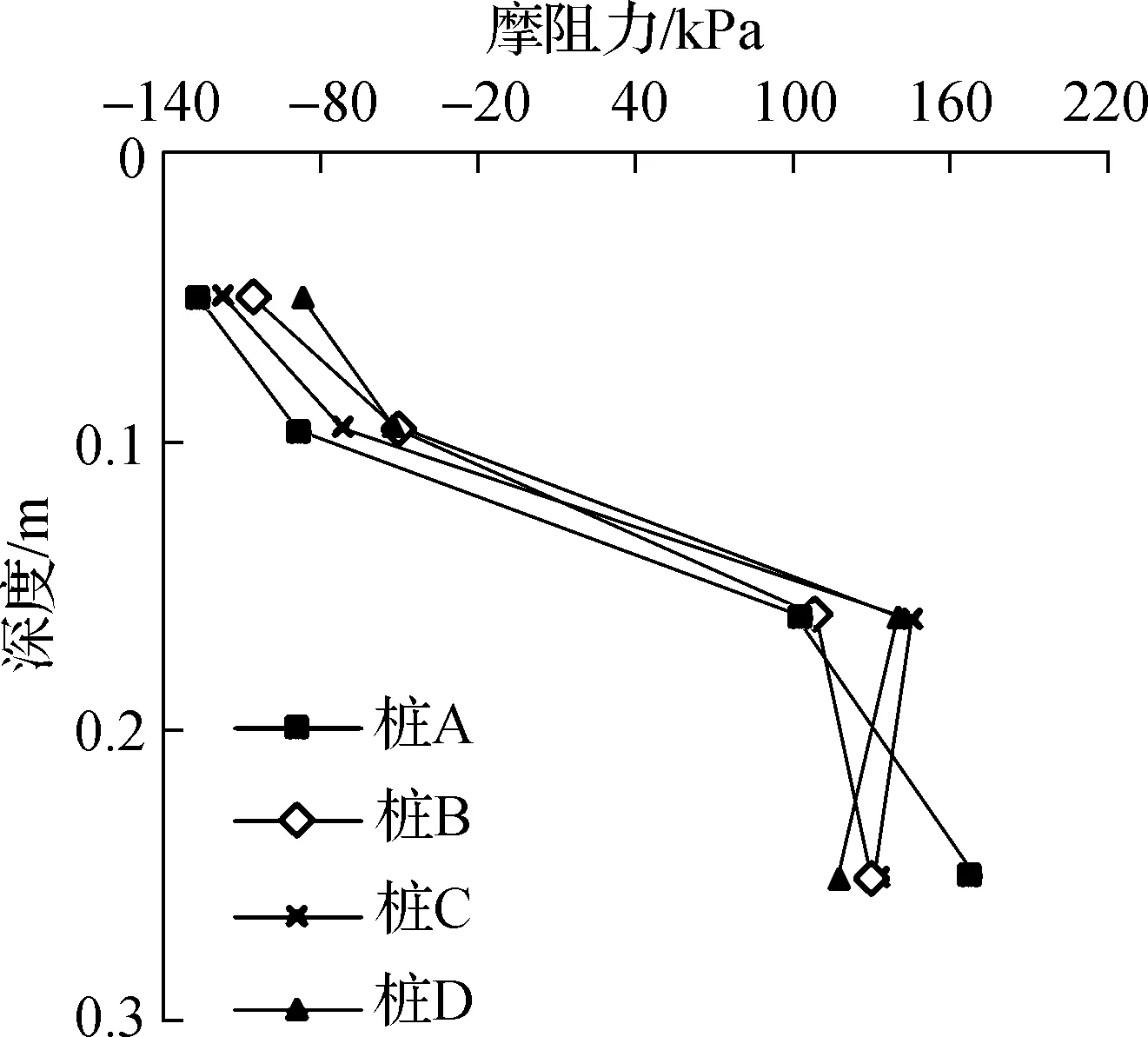
(b) 摩阻力

2.3 桩土荷载分担比与桩土应力比

图7为不同厚度垫层模型的桩土荷载分担比随荷载变化曲线.由图可知，荷载较小时，地基土承担较多的上部荷载；随着荷载的增大，桩基逐渐发挥作用，桩承担荷载增加，超过地基土承担荷载；当荷载达到380 kN (即摩阻力为600 kPa)后，桩土荷载分担比逐渐稳定，不再变化.当垫层较薄时，起始桩土荷载分担比相差不大，但是稳定后桩承担的荷载比地基土大得多；垫层较厚时则相反，起始时桩土荷载分担比相差较大，稳定后桩承担的荷载与地基土较为相近.对于模型MX36-2、MX36-4和MX36-6，最终桩和土的分担比分别相差16.8%、9.6%和2.4%.说明垫层越厚，垫层对桩、土变形协调能力越好.

图7 不同厚度垫层模型桩土荷载分担比

不同厚度垫层模型的桩土应力比见图8.由图可知，桩土应力比随着荷载增加而增加，最终趋于稳定.相同荷载条件下，垫层越厚，桩土应力比越小，但随着厚度的增加，垫层厚度对桩土应力比影响逐渐变小.模型MX36-2、MX36-4、MX36-6的起始桩土应力比分别为9.91、8.43、6.04，最终桩土应力比分别为15.69、11.73、9.22.

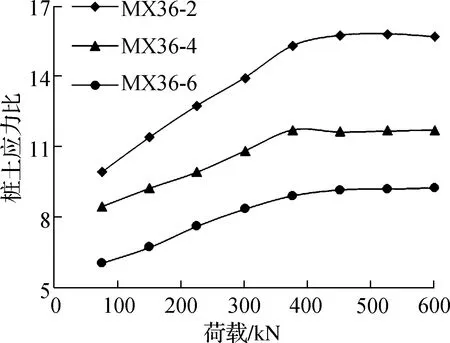
图8 不同厚度垫层模型桩土应力比

3 多尺度耦合数值模拟分析

3.1 模型建立

采用优化后的PFC3D-FLAC3D离散-有限差分耦合分析方法[14]，对非接触桩箱复合基础竖向承载力室内模型试验进行建模分析.数值模型分为2个部分：上部为离散元模型，由沉箱和垫层组成；下部为有限差分模型，模拟桩复合地基.考虑计算机的计算效率，为节约计算机内存资源，取室内试验1/4模型进行建模.

建模过程中将沉箱考虑为刚体，采用块体单元(Clump)进行模拟.垫层采用与室内试验垫层级配一致的球单元(Ball)，粒径为2～5 mm.球单元之间采用线弹性模型、滑动摩擦模型以及非黏滞阻尼模型，其法向刚度和剪切刚度均为10 MN/m，摩擦系数为0.55.垫层和沉箱之间的接触为线性连接模型.

在有限差分软件中，采用实体单元模拟桩基础，为保证模型桩与试验桩的刚度一致，模型桩参数为

式中，E′、ρ′分别为数值模型桩的弹性模量和密度；E、ρ分别为Q235钢的弹性模量和密度；A′为模型实心桩的横截面积；A为试验管桩的横截面积.模型桩密度为2.34 g/cm3，弹性模量为63 GPa，泊松比为0.33.

地基土采用莫尔-库伦模型，相关参数与室内试验一致.土层密度为1.59 g/cm3，压缩模量为28 MPa，泊松比为0.22，摩擦角为35°，黏聚力为0.2 kPa.桩和地基土之间接触面采用库伦(Coulomb)滑移单元，允许相对滑动，接触面法相刚度为1 GN/m，剪切刚度为0.5 GN/m，摩擦角为28°，黏聚力为0.6 kPa.

3.2 多尺度耦合模型验证

图9为室内试验与模型计算得到的沉箱基础荷载-位移曲线.由图可知，试验结果与模拟结果较为吻合.但当荷载较小时，相同荷载条件下室内试验的沉箱沉降更大；荷载较大时则相反.且垫层越薄，小荷载条件下沉箱沉降试验值和模拟值差距越大.这可能是因为离散元中球颗粒为圆形刚体，无法发生破碎，数值模型中垫层压缩模量呈线性变化，但是实际上垫层角砾压缩模量并非线性变化，从而导致试验值与模拟值产生误差.图10给出了600 kN荷载条件下不同垫层模型中心桩桩A的桩身轴力试验值与模拟值对比.由图可知，模拟值小于试验值.然而，模拟值与试验值的整体变化规律一致，均呈现出垫层越厚、桩身轴力越小的趋势，且所得桩身中性点位置基本一致.因此可以认为，建立的离散-有限差分多尺度耦合数值模拟分析模型基本能够正确模拟竖向荷载条件下非接触桩箱复合基础的力学性能.

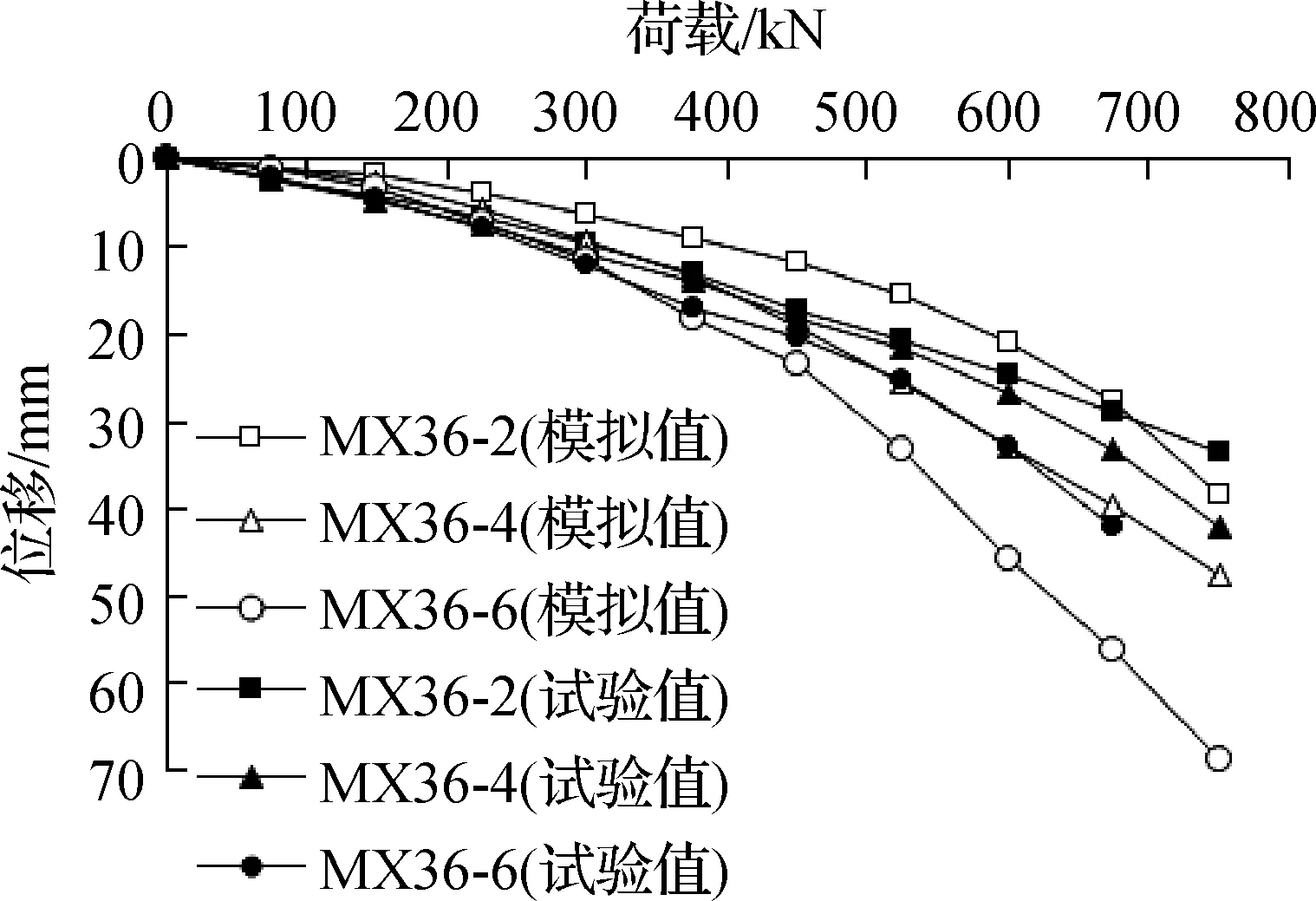
图9 沉箱基础的荷载-位移曲线

4 多尺度对比分析

4.1 宏观试验结果分析

图11为600 kN荷载条件下模型地表土体及桩的竖向位移.由图11(a)可知，沉箱下部地基土沉降呈中间大、两边小的蝶形.垫层越厚，沉箱下部相同位置处的地表土体越大，但土体沉降也越不均匀.这是因为当垫层厚度较小时，垫层对整个地基土体的变形协调能力较弱，且沉箱刚度很大，土体沉降受上部沉箱影响比较大.

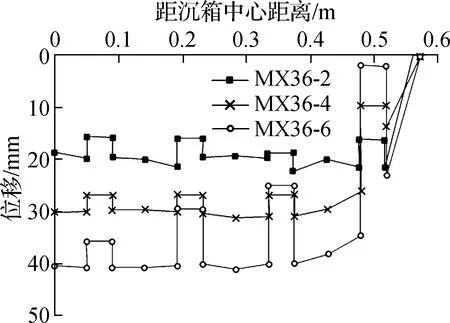
由图11(b)可知，随着荷载的增大，垫层及地基土被压缩，从而发生较大竖向位移，而桩基础沉降小于垫层及地基土沉降，桩顶逐渐高于地基土表面，桩和土之间形成相对位移.对比图11(a)中地表土体的竖向位移，图11(b)中凸起部分为桩顶位移.由图可知，垫层越厚，桩基不均匀沉降越大，模型MX36-2、MX36-4、MX36-6的桩基不均匀沉降分别为0.34、17.18、33.90 mm.除此以外，当垫层为6 cm时，桩基沉降也呈中间大、两边小的趋势；而模型MX36-2的几根桩沉降一致，模型MX36-4靠近中心的3根桩沉降一致.可以发现，垫层下部桩基沉降与周围地基土沉降规律一致.600 kN荷载条件下，模型MX36-2由中心桩到外侧桩的刺入量分别为3.4、3.5、3.6、5.1 mm，桩基刺入量差别不大；而模型MX36-6由中心桩到外侧桩的刺入量分别为8.0、13.5、18.6、33.9 mm.因此，外侧3根桩相比于中心桩，由中心向外桩顶刺入量分别增加了68.75%、132.5%、323.75%.

(b) 桩A的轴心横剖面

4.2 细观试验结果分析

以750 kN荷载条件下模型MX36-6为例，绘制通过桩A中心轴长轴方向的模型剖面，并将颗粒位移表示成矢量图，结果见图12.由图可知，随着加载的进行，沉箱向下嵌入垫层，桩向上刺入垫层.沉箱下部垫层颗粒主要发生向下位移，沉箱侧面垫层颗粒以水平位移为主.为进一步分析加载过程中颗粒位移变化情况，绘制600 kN荷载条件下模型MX36-6的颗粒竖向位移云图，结果见图13(a).由图可知，桩顶区域以外的颗粒竖向位移基本一致，桩顶颗粒竖向位移相较于桩顶区域以外明显减小，且边桩桩顶颗粒位移小于中桩桩顶颗粒位移.模型MX36-6中边桩桩顶出现了明显的土拱效应，中心桩桩顶未能形成完整核心区.

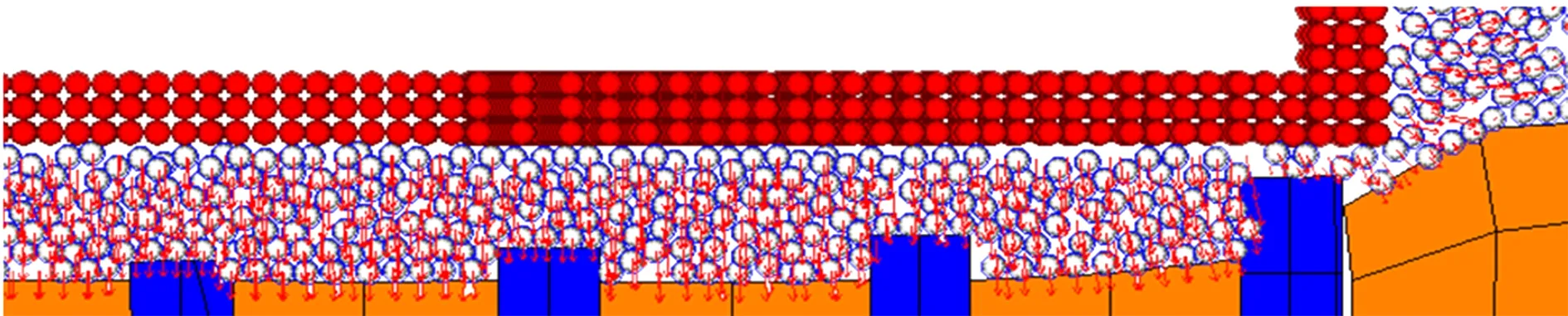
图12 750 kN荷载条件下模型MX36-6垫层颗粒位移矢量图

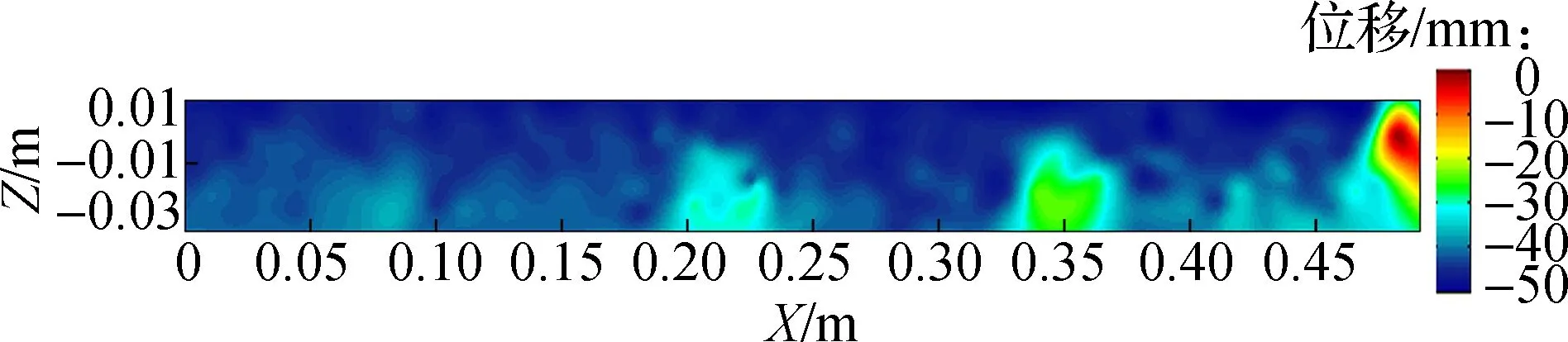
(a) 竖向位移云图

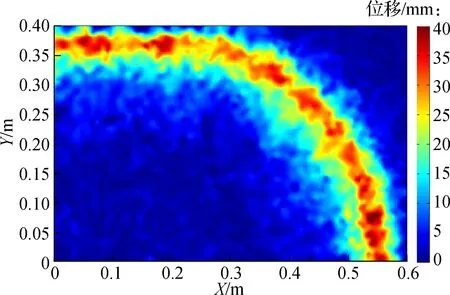
(b) 水平位移云图

以600 kN荷载条件下的模型MX36-6为例，绘制模型水平剖面垫层颗粒水平位移云图，结果见图13(b).由图可知，竖向荷载条件下沉箱外边缘部分颗粒被挤出沉箱下部.长轴方向距沉箱中心0.4 m以外的垫层颗粒在竖向荷载作用下发生水平位移，这一位置与模型MX36-6地表土沉降拐点一致，即垫层颗粒出现明显水平运动的起始点与地基表层土沉降出现拐点位置相一致.

5 结论

1) 建立了离散-有限差分多尺度耦合数值模型，将计算结果与室内试验结果相对比，证明该模型能够正确模拟竖向荷载条件下非接触桩箱复合基础力学性能.

2) 非接触桩箱复合基础荷载位移曲线为缓降形，下部地基土变形呈中间大、两边小的蝶形.相同荷载条件下，垫层越厚，沉箱沉降越大，且相同位置处地表沉降越大.

3) 相同荷载条件下垫层越厚，桩基础不均匀沉降越大，桩基础相对于垫层刺入量越大，相同位置处桩基础中性点越低，但垫层对地基土及桩的变形协调功能越好.

4) 沉箱下部垫层颗粒主要发生向下位移，桩顶区域以外颗粒竖向位移基本一致，桩顶颗粒竖向位移相较于桩顶区域以外明显减小.靠近沉箱边缘处颗粒出现明显水平位移，垫层颗粒出现明显水平运动的起始点与地基表层土沉降出现拐点位置相一致.