借助画图策略，建构数学模型

聂应波

【摘要】“植树问题”是数学广角的经典问题，要解决这一问题，可以采用建构普遍的数学模型的方法。笔者就如何借助画图策略，帮助学生有效地理解问题结构、建构数学模型，结合自己的教学实践，给出了具体的思考与建议。

【关键词】画图策略；数学模型；植树问题

“植树问题”是数学广角的经典问题，就“植树问题”这一经典课题而言，往常大多数教师特别重视关于“植树问题”三种不同类型的区分。即两端都栽、两端不栽、一端栽一端不栽，并要求学生牢牢地记住相应的计算法则（“加一”“不加不减”“减一”）。学生虽然会解决这一问题，却不能把植树问题的解决方法与生活中相似的现象进行知识链接，只是在“机械应用”，思维的灵活性明显不够。其实这三种问题都有着相同的数学结构，即可以被归结为同一个数学模型。基于此，帮助建构植树问题的数学模型将是本节课的教学重点，也是教学难点。那么如何有效地帮助学生理解问题结构，建构数学模型呢？在教学中我做了如下的尝试。

一、借助画图引发认知冲突，感悟相同中的不同，初识模型

典型的植树问题与学生先前学习的平均分问题有着紧密的联系。因此，这节课的教学首先从简单的平均分问题入手引出植树问题。

课件依次出示：20个苹果，每只小猴子5个，可以分给几只小猴子？

生：20÷5=4（只）。

师：20个人乘车，每辆车可载5人，需要几辆车？

生：20÷5=4（辆）。

师：想想为什么它们都能用20÷5=4来解决呢？

生：都是平均分。

师：究竟为什么呢？请图来说话，让我们借助图，再次来理解一下究竟是为什么呢？（课件出示下图）

师：这两题，穿着的外衣不一样，一个简单的图就能让我们看清其实它们的实质是一样的，都是求20里面有几个5。

师：这次挑战升级了，大家还有信心吗？

课件出示：在一条长20米的小路一边植树，每隔5米种一棵，一共要种多少棵树？

生：4棵、5棵……

师：到底要种多少棵树？怎么验证？

在学生猜想植树棵数的基础上引发矛盾冲突，学生自发地产生画图验证的需求，感悟到在解决问题时可以借助画图来理解。

二、借助画图引导对比，发现数量中的关系，理解模型

（一）画图验证

师：种树时要符合什么要求？画图该怎么表示？

生：每五米种一棵，就是每两棵树之间的间隔长度为五米，在图上可以用5厘米表示。

师：好的要求明确，方法也有了，那么请大家画一画，想一想到底需要几棵，先独立思考再在小组内交流你的想法。（巡视，并挑选代表画在黑板上。）

师：好多同学已经通过画图验证了自己的想法，下面一起来请同学结合图来说说是自己是怎么种的？种了几棵，第一棵树种在哪里？

（二）列出算式

师：画图后有了不同的答案。我们能否用算式來表示这些答案呢？

生：一齐列式。（先列两头都种的，再列两头都不种的，最后列只种一头的）

（三）对比理解

师：20÷5=4，求出的是什么呢？

生：4个间隔。

师：板书20÷5=4（个），这种植树的方法四个间隔刚好是四棵树，那为什么四个间隔刚好就种了四棵树呢？谁来到图上指指这四棵树在哪？四个间隔又在哪呢？（带着学生指一指一棵数一个间隔）

师：这样一棵树刚好对着一个间隔，在数学上，我们把称为“一一对应”。

师：（依次指着两头都种20÷5=4（个）和两头不种的）那这里为什么还要加1呢？这里为什么要减1呢？谁到上面指一指？为什么要加一棵呢？引导学生解释原因，说明理由。渗透一一对应的思想，理解棵树与间隔数之间的关系，感悟植树问题模型。

（四）归纳命名

师：谁能给这三种不同的方法取个名字呢？两头都种，只种一头，两头都不种。

这个过程中始终借助图，让学生直观得发现植树问题的三种情况：两头都种、只种一头、两头不种。引导学生看图并直观演示，让学生从图中看到关系，理解“棵树、间隔数”，感悟“一一对应”思想。

三、借助画图类比迁移，体会不同中的相同，建构模型

（一）学生结合图探究30米的路

师：同学们我们可能在20米的路上种树，还有可能在15米、30米、若干米的路上种树，那结果又是怎样的呢？就以30米为例，试一试师课件出示题目。（生独立完成）

生：结合图汇报结果。

（二）脱离图研究50米、100米的路

师：若路又变长了，变成了50米，100米还愿意画下去吗？不画了，谁能快速列式呢？（结合学生回答板书算式）

（三）引导发现棵树与段数之间的关系

师：无论路长多少米，只要两头都种棵树，就会是怎样的呢？两端都不种呢？能否说说椴树与棵树之间的关系呢？同桌互相说说。

生：答略。（师板书三种关系）。

（四）总结提升反思方法

师：若是一千米呢？是什么帮助我们发现其中的奥秘的？（板书画简图找规律）

（五）联系生活，建构模型（课件出示下图）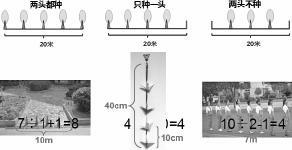

师：什么相当于树？图中的情况相当于我们种树的哪一种？

在学生得出棵树与间隔数之间的数量关系后，通过变换路的长度再次探索植树棵树的问题，逐步将植树问题的三种不同情况进行提炼，得出棵树与间隔数之间的关系，凸显出数学结构，抽象成数学模型。

四、借助画图解释规律，沟通问题中的联系，运用模型

而建立模型思想的最后一个环节是通过模型去求出结果，并用此结果去解释讨论其在现实问题中的意义。在最后练习的环节以图文结合的形式出示一个题组，充满浓郁生活气息，让学生运用模型解决问题。

总之，尽管“植树问题”可以被看成提供了一个很好的“现实原型”，但在教学中我们还需要超出这一特定情境，设法由一个到一类渗透一种数学规律的思想，深化对模型思想的理解，在此过程中凸显画图在解决问题中的作用，画图策略成为模型运用的有力支撑。

【参考文献】

[1]曹健.巧借数学建模，启发学生思维[J].江西教育，2020（18）.