矿岩三维运动对主溜井井壁碰撞范围的影响

殷 越 路增祥，2 马 驰

（1.辽宁科技大学矿业工程学院，辽宁鞍山114051；2.辽宁省金属矿产资源绿色开采工程研究中心，辽宁鞍山114051）

金属矿山地下开采中，主溜井承担着矿石与废石的下向运输任务，具有服务年限长的特点，是竖井箕斗提升矿山的重要开拓工程之一［1-4］。国内外矿山的溜井使用经验表明，溜井工程的顺畅使用是保障矿山生产顺利进行的关键［5-8］。但是，复杂的溜井工程地质条件和恶劣的溜井使用环境，导致溜井频繁发生变形破坏现象［9-11］，轻则刷大溜井直径，造成溜井变形［12-14］，严重时会发生坍塌致使溜井系统报废。如湖北程潮铁矿［15］、安开铁矿3#主溜井［16］、南非kloof金矿［17］、加拿大魁北克省北部Brunswick矿等十余家地下矿山［18-19］都因溜井发生严重变形破坏造成溜井报废或停产返修，严重影响了溜井的使用效果，给矿山企业造成了巨大的经济损失。

主溜井的使用特性决定了矿岩在溜井中的运动状态难以量测，在生产现场观测所得的数据难以揭示矿岩运动特征与井壁破坏特征之间的相互关系。因此，目前针对溜矿段井壁破坏的研究工作主要围绕确定井壁受冲击后的破坏范围方面开展。罗周全等［20］构建了主溜井受矿石冲击的损伤理论模型，得到了溜井的破坏范围，并与现场实际探测结果进行对比，验证了其合理性；秦宏楠等［21］以运动学理论为基础，结合离散元数值分析等得到井壁的冲击位置；宋卫东等［22］根据相似理论构建了采区溜井物理模型，通过试验分析得到了井壁的破坏区域。上述研究为揭示溜井井壁的破坏特征提供了重要的理论依据。

研究溜井中矿岩的运动特征与井壁破坏范围之间的关系，对于定量计算井壁的破坏范围意义重大。本研究以辽宁省辽阳市某铁矿主溜井为研究对象，以运动学理论为基础，建立矿岩块与井壁初次碰撞前的运动速度、轨迹与溜井结构参数、速度方向角之间的关系式，构建井壁冲击区域的理论计算模型，重点分析方向角对初始碰撞位置的影响，同时通过物理模拟试验验证所建模型计算结果的准确性；结合多组溜井放矿试验，分别从单个矿岩块碰撞与矿岩流冲击两个角度分析矿岩与井壁碰撞范围及其分布特征，研究结果可为溜井系统设计与优化、治理修复和管理方案制定提供依据，以期保障溜井的稳定性。

1 工程概况

辽宁省辽阳市某铁矿采用下盘竖井开拓，无底柱分段崩落法采矿。该矿主溜井为垂直溜井，位于-40～-110 m水平，主溜井直径为5.0 m，井筒围岩整体比较稳定，节理不甚发育。该矿阶段运输采用4 m3底侧卸式矿车运输，矿石从-40 m卸矿站进入主溜井，经-110 m主溜井下部的破碎站破碎后，经皮带运输、装载硐室进入箕斗后提升至地表。该矿主溜井及溜槽主要结构参数如表1所示。

该矿主溜井经过多年使用，产生了较严重的井壁变形与破坏，测量结果显示，该段主溜井井口以下4 m至9 m处受冲击变形破坏严重。

2 井壁破坏特征理论分析

研究矿岩块在溜井中运动时，本研究进行如下假设：①矿块和井壁均为弹塑性体，井壁为壁面平整的直筒，且各部分岩体岩性相同；②将矿块简化为球形，质量均匀分布；③矿块在溜井中运动时不考虑自转及矿块间的相互作用，矿块运动过程中质量不发生变化；④矿石与矿车的摩擦系数为一定值；⑤矿石以初速度v进入卸载溜槽，该速度值为一定值。

2.1 井壁冲击区域模型构建

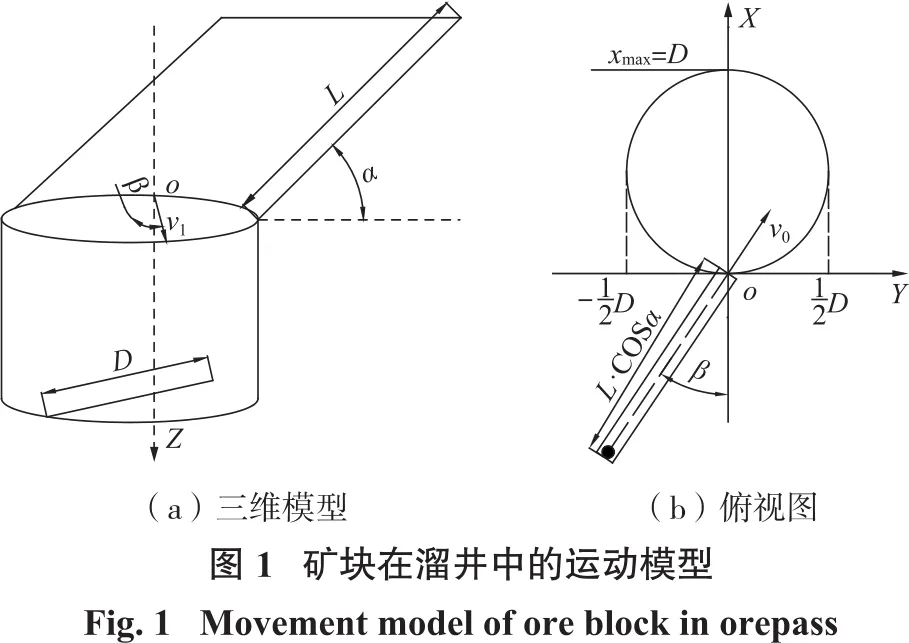
通过图1（a）可知，当矿岩块从溜槽进入主溜井时，由于方向角的变化造成初始运动状态的不同，导致冲击区域的不同，通过图1（b）可知，由于矿岩块在溜井中只受到重力作用，则不同方向角下矿石在XO-Y面上运动轨迹的投影长度小于等于溜井直径。

2.2 矿石运动轨迹与井壁冲击区域理论分析

矿块进入溜井后，在重力作用下作斜下抛运动，其运动轨迹类似于一段抛物线，直至冲击井壁。如图1所示，对溜井运动模型建立空间直角坐标系，设矿岩块从O点进入斜溜槽。

根据运动学公式分析可知，当矿石到达O点时，速度v0大小为

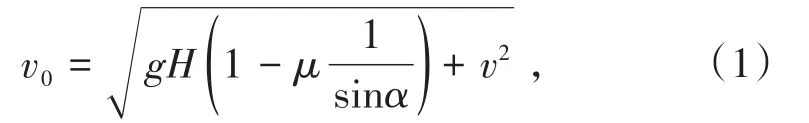
式中，g为重力加速度，m/s2；H为斜溜槽高度，m；μ为矿岩块与斜溜槽的摩擦系数；α为斜溜槽角度，（°）；v为矿块离开矿车时的速度，m/s。

以此为基础在溜井运动模型上建立空间直角坐标系，可以得到如下运动方程组：

式中，v0为矿岩块刚离开溜槽进入溜井时的速度，m/s；t为矿岩块从O点开始首次冲击井壁所需要的时间，s；α为初速度与水平方向的夹角，在进入溜井的一瞬间，α与斜溜槽倾角方向一致，（°）；β为初速度与垂直面的夹角，β的取值范围为(-90°,90°)。式（2）（xt，yt，zt）所覆盖的区域共同确定了溜井受到冲击的范围。

由式（2）可知，矿岩首次与井壁的碰撞范围与矿岩进入溜井时速度大小、方向、运动耗时以及方向角等有关。当主溜井结构参数一定时，矿岩进入溜井速度是一定的，此时速度方向角绝对值越小，矿岩与溜井的碰撞高度、碰撞点的y坐标值越小，x坐标值呈增大趋势。

2.3 井壁冲击区域模型构建

通过图1（a）可知，当矿岩块从溜槽进入主溜井时，由于方向角的变化造成初始运动状态不同，导致冲击区域的不同。通过图1（b）可知，由于矿岩块在溜井中只受到重力作用，则不同方向角下矿石在XO-Y面上的运动轨迹投影小于等于溜井的直径，溜井发生碰撞的运动时间t为

式中，t的取值范围为[0,tmax]，当方向角为0°时所需时间最长。

从式（2）、式（3）可以看出，在图1的运动模型下，受冲击的范围与α、β和v的大小密切相关。而矿山生产实际中，α值取决于溜井的结构设计与施工，是一固定值，因而矿石初始运动状态对其冲击井壁的时间和范围的影响，实质上是由方向角β决定的。

根据该矿主溜井斜溜槽和溜矿段结构参数（表1），并结合式（1）、式（3），根据假设④、⑤，μ，v为常数，摩擦系数取0.5计算，得到矿石运动到O点的速度v0=7.67 m/s，矿石与井壁发生碰撞的最大时间tmax=0.92 s。

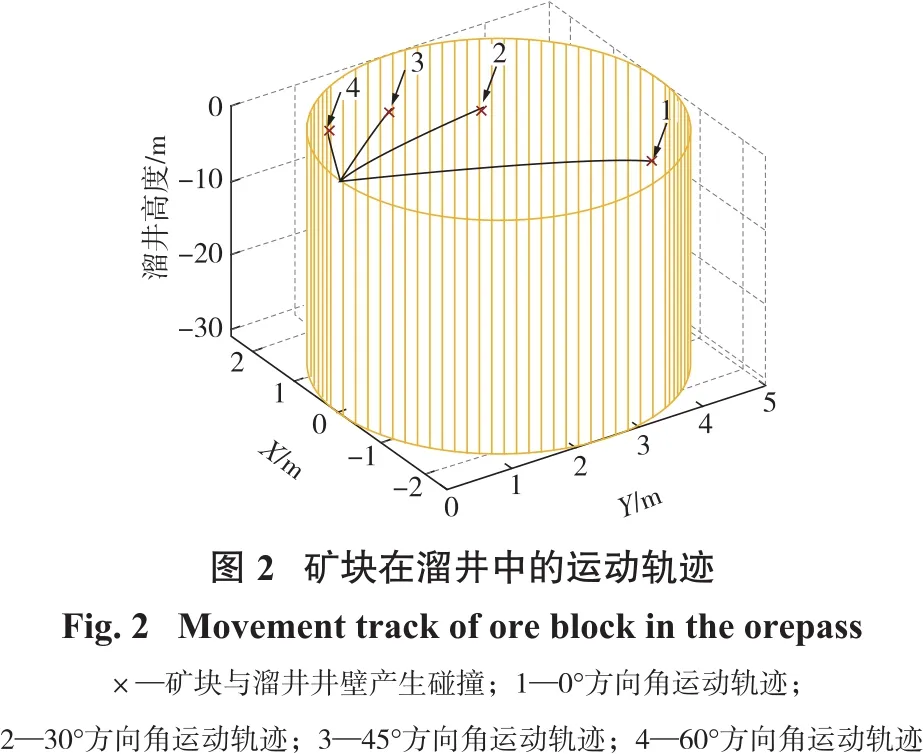
如图2所示，根据主溜井斜溜槽和溜矿段结构参数构建溜井冲击点模型，坐标轴上的数值代表溜井高度和断面尺寸。通过模型可以看出，随着方向角逐渐增加，矿块对于井壁冲击的位置不断提高，从井口下一直延伸至井口正对面9.23 m处形成两条对称的弧形斜冲击带。

3 室内试验与分析

3.1 室内试验相似条件及模型

根据矿山溜井实际结构参数及相似理论，构建了溜矿段相似实验平台，矿石材料与井壁材料相似比取1，尺寸相似比取10，则尺寸相似比ρL为

式中，Lp为原型线性长度；Lm为模型线性长度。

运动相似是指矿石在主溜井溜矿段中的实际运动轨迹与在相似性模型中的运动轨迹线呈几何相似，并且所需要的运动时间与实际需要的时间成一定比例，假设时间相似比为原型时间tp与模型时间tm之比，则：

则速度相似比ρv为

式中，vp为原型速度；vm为模型速度。

加速度相似比ρa为

式中，ap为原型加速度；am为模型加速度。

坐标原点为斜溜槽卸矿口与主溜井相连处（0，0，0），v0为矿石刚从斜溜槽进入溜井时初始速度，根据速度相似比v0=2.43 m/s。

如图3所示，为了便于观察井壁受冲击破坏的位置，在溜井实验平台内通过理论计算，在冲击区域四周井壁布置相似材料，用来验证实际破损区域，井壁相似材料采用工业石膏制作。将石膏均匀涂抹于PVC管材内壁中，防止石膏受冲击后整块破裂影响试验结果。

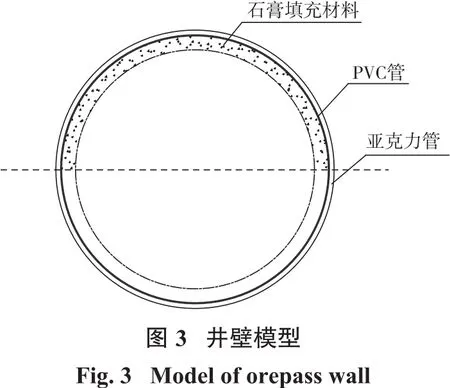
为更好地符合矿山溜井实际情况，对井壁相似材料进行打磨，打磨后上下表面最大不平行度小于等于0.001 m，模具制作完成后，对石膏表面进行了喷漆处理。试验过程中井壁受到冲击时，表面石膏会发生脱落，既能够观察不同方向角下井壁受冲击后发生破坏的区域、形状，也能观察井壁的破坏形式，包括横向上冲击破坏和纵向上的剪切破坏。模具制作完毕后，对石膏表面进行喷漆处理。试验过程中井壁受到冲击时，表面石膏会发生脱落，露出里面石膏的颜色，便于观察不同方向角下井壁受冲击后发生破坏的区域。进行溜井相似试验时，选用直径50 mm以下不同形状的矿岩块进行井壁冲击试验，多次冲击后井壁的破坏范围分布如图4所示。

分析矿岩块对井壁的冲击情况发现，相同方向角下的多次冲击并未集中作用在井壁的同一点上，而是分布在理论计算得到的冲击点周围，位置误差小于4.72%。这主要是由于以下原因所造成的：

（1）试验过程中采取的单个矿块溜放过程，矿岩块的直径远小于溜槽宽度，在斜溜槽中运动时具有不可控性和一定范围内的随机性。

（2）理论计算时将矿岩块看作均匀的球体，而实际上矿岩块是具有不同的体积与形状的，所以会形成破坏面，同时通过观察井壁破坏情况可以发现，不同形状的矿岩块对井壁的冲击破坏程度不同。

3.2 矿石流冲击下井壁碰撞范围分布

矿山现场生产中，矿岩对溜井壁的冲击是以矿岩流的形式进行的。因此，研究矿石流冲击下井壁受冲击的范围更具有实际意义。矿石流冲击时，选用磁铁矿（黑色）矿石碎块，其颗粒级配组成如表3所示。

根据表3的粒径组成，按质量百分比称量不同粒径组的矿岩块质量，然后将称量后的矿岩块混合均匀，一次卸矿量为0.1 m³。图5反映了不同冲击次数下溜井井壁碰撞分布范围。从图中可以看出：随着溜矿次数的增加，矿岩冲击井壁的位置与范围逐渐趋向集中，反映了矿石流冲击溜井井壁时产生了累积损伤效应。

4 结 论

（1）通过构建溜井溜矿段放矿实验平台和矿石运动分析模型，揭示了井壁首次受冲击破坏的区域与溜井结构参数、矿岩速度、方向角之间的关系，建立了矿岩块与井壁产生第一次碰撞范围的理论计算模型。

（2）矿岩对井壁的冲击位置不仅与其进入溜井时的速度有关，还与其进入溜井时的方向角密切相关，当溜井结构参数一定，速度方向角增大时，井壁受到冲击的位置不断提高，经过理论推导计算得到会在井口下9.23 m处形成两条对称的弧形冲击带。

（3）试验得到的矿石冲击区域比理论计算得到的位置更高，冲击区域更大，造成的破坏范围更广，不同块度的矿石对井壁的破坏范围也有所不同，反映出理论推导结果和实际情况存在一定的误差。

（4）矿岩流对井壁的反复冲击试验表明，井壁受冲击的位置与范围趋向集中，产生了累积损伤效应。