基于动态加速度显式数值流形法的边坡稳定性分析

余荣春 莫敏华

（广西工业职业技术学院建筑工程学院，广西南宁530001）

随着露天开采深度逐步增加，露天矿边坡的稳定性控制变得愈加重要。理想的方法是可以预测滑落面位置以及发生滑落的条件，并且可以预测失稳边坡的运动过程。常用的设计方法有经验设计方法、物理模型试验、极限平衡法以及数值方法。经验设计方法是利用已有的实践经验设计坡角，该方法虽然简单，但精度有待提高。物理模型试验是在可控环境中模拟实际坡度条件，并通过修改参数来研究其对边坡稳定性的影响，该方法通常耗时较长且成本高。极限平衡法［1］是假设每一个可能的破坏面，然后相应地计算安全系数，该方法已被广泛应用于岩质边坡设计。上述方法大体上将每个块体简化为刚体，且失稳面在某种程度上必须事先已知，无法描述失稳边坡的运动过程。

近年来，数值方法凭借高效、高速、低耗的优势得到迅速发展，该方法可通过计算块体中的应力和位移，采用各种本构关系，来对复杂边坡进行参数研究。数值方法可分为基于连续介质的方法（如FDM，FEM，BEM）和基于非连续介质的方法（如UDEC［2］，3DEC［3］，DDA［4］）。前者可处理的不连续块体数量较为有限，且无法准确模拟边坡失稳的动态过程。后者在建模过程中可体现出岩体的不连续性，并能有效模拟块体运动，但该类方法很难模拟完整岩石的破坏情况。岩质边坡破坏是一个典型的连续—不连续面组合问题，需使用混合连续介质—不连续介质的方法进行模拟。STEAD等［5］开发了一种混合有限/离散元程序ELFEN，并成功应用于模拟岩质边坡破坏。在ELFEN中，提出了两种插入离散裂缝的方法，但它需要非常精细的网格来准确地捕获断裂方向。具有人工节理的离散块体系统的DDA也被用于模拟完整岩石中的破坏［6］，通过将满足失效标准的人工节理转换成真实节理来实现压裂，然而其预测的裂缝轨迹取决于块体的提前离散化结构。Itasca的颗粒流编码（PFC）具有完整岩石和节理的建模能力，在解决岩体相关问题方面显示出了强大的能力，PFC2D软件已被用于研究节理岩质边坡的稳定性［7］。

数值流形法（NMM）是另一种连续—非连续组合方法。NMM最初是由SHI［8-11］开发的，后来被用于研究裂纹扩展等问题［12-14］。NMM的显著优势表现为：①用于生成NMM模型的网格完全不受求解域几何形状的影响，这使得网格划分更加方便，并且完全避免了非连续演化过程中的网格重新划分；②不连续面通过双覆盖系统直接建模，不需要预设界面单元；③将有限元法和DDA相结合，使得在统一的框架内对连续体、从连续体到不连续体的过渡以及不连续体进行建模成为可能。在动力学问题求解中，逐步积分法优势显著，其中包括隐式积分法及显式积分法，隐式积分法主要有中心差分法、Wilson-θ法［15］及Newmark-β法［16］等，中心差分法是显式积分法的最优代表［17-18］。王进廷等［19］对多种显式方法进行了详细分析，并对其稳定性及精度进行了比较。李常青等［20］针对位移项进行了三步二阶显式积分方法的推导及验证，增强了其运算稳定性。

尽管NMM方法存在诸多优势，但在处理大规模非线性动力学运算时存在计算精度不高等问题。显式积分虽然省去了对耦联方程组求解的过程，但在运算精度方面优势显著。为此，本研究借助NMM的两套覆盖系统可在同一计算架构下处理连续—不连续问题的优势，并结合显式积分算法提出基于动态加速度显式积分算法的NMM，同时通过控制应变增量大小保证运算的收敛性。在此基础上，将改进后的基于动态加速度显式积分算法的NMM应用到某露天矿边坡稳定性分析中。

1 基于动态加速度显式积分算法的NMM

1.1 NMM双覆盖系统

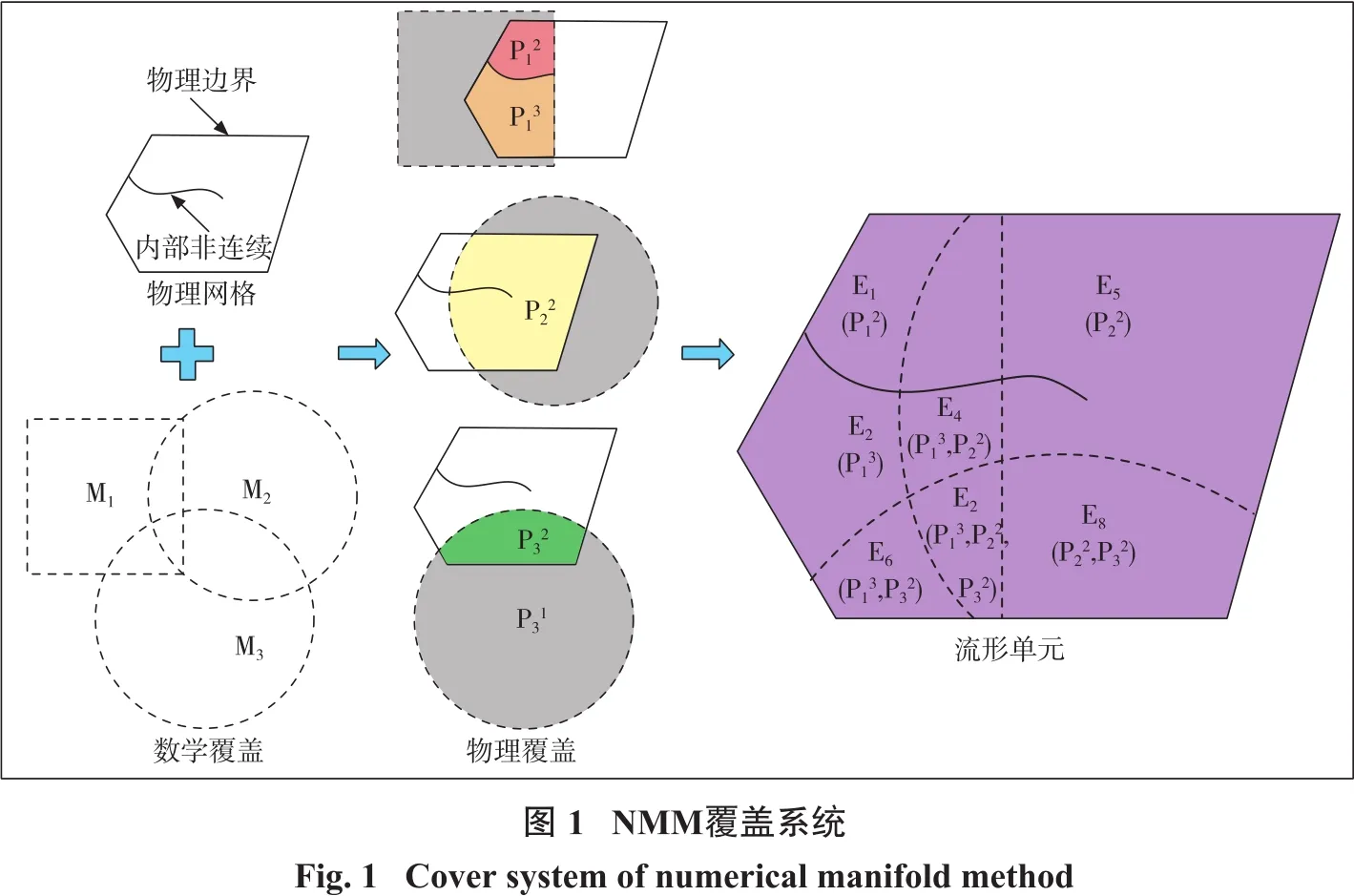
NMM使用一组重叠的片覆盖问题域，片的边缘不必与外部边界或内部不连续点重合。每个片被称为数学覆盖（Mathematical Cover，MC），用Mi表示，其中i是该问题所使用的MC的数量。外部边界和内部不连续区域（如材料边界、裂隙灯）与每个MC相交，切割形成若干独立的片，如果该片是在问题域，则称为一个物理覆盖（Physical Cover，PC），用Pj表示，其中j是MC被切割形成片的数量。图1所示为NMM覆盖系统示例，矩形片M1，圆形片M2和M3相互叠合形成数学覆盖MC，经边界与内部裂纹切割，形成一系列物理片（如P11，P22，P32等，其中下标和上标分别代表数学覆盖的序号及物理覆盖的序号），即物理覆盖PC。物理覆盖PC相互重叠区域称为流形单元（Manifold Element，ME），例如 E1，E2，E3等。该双覆盖系统在生成求解域时不需要考虑求解域几何形状，便于网格划分，在求解过程中也不需要重新划分网格，且不必预设界面单元。

在物理覆盖系统形成之后，NMM在其上赋予局部位移近似函数，一般选择多项式进行局部位移近似：

式中，x为位移矢量；PT为多项式的基函数矩阵；d为位移自由度列阵；k为PC序列号。

1.2 动态加速度显式积分算法

定义时间步长固定，加速度在单个时间步长内呈线性变化，则加速度的斜率为

加速度方程可表示为

式中，b1为系数。

通过积分运算可得速度、速度增值及位移函数分别为

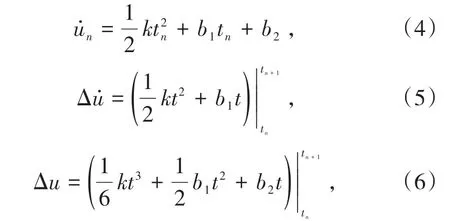
式中，b1、b2为系数。

将式（2）至式（6）联立求解，可得：

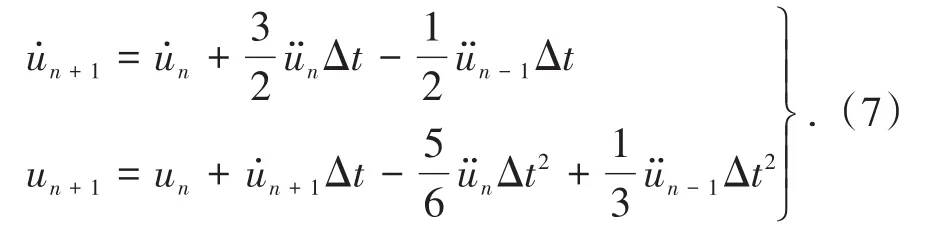
为控制预设条件加速度在单个时间步长内呈线性变化的误差，本研究采用显式积分算法计算各加速度，即：

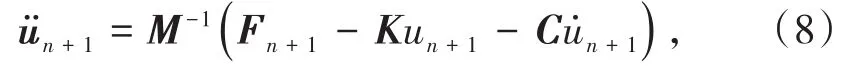
式中，M、K、C、F分别表示质量矩阵、刚度矩阵、阻尼矩阵及外力矢量。

2 动态加速度显式数值流形法稳定性测试

为测试动态加速度显式数值流形方法在不同运算步数下的稳定性，本研究选用应力波冲击隧道经典模型，运用动态加速度显式数值流形方法计算并分析，并与传统NMM及解析解对比。该模型弹性模量E=10 000 MPa，泊松比ν=0.25，容重γ=27.0 kN/m3。图2显示了不同时步运算结果的收敛性，结果表明在第1.0×107时步、第2.0×107时步、第3.0×107时步、第5.0×107时步均表现出了良好的收敛性。

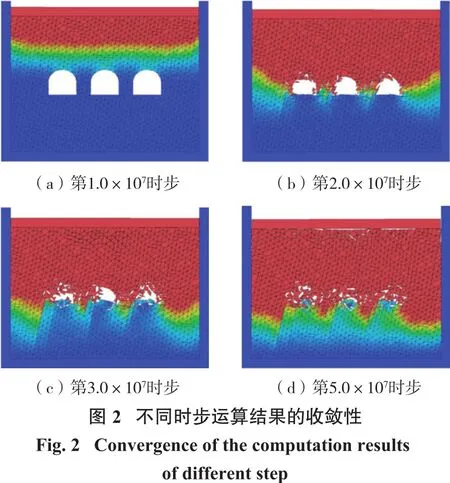
动态加速度显式数值流形方法、传统NMM及解析解的对比结果如表1所示。由表1可知：该方法比传统NMM精度高，且总时步数越多，块体数目越多时，动态加速度显式数值流形方法的精度越高，优势愈明显，当总时步数达到108、块体个数达到107数量级时，与解析解误差接近于0，印证了该方法在处理大规模复杂动力学问题方面的可行性及准确性。

3 露天矿边坡稳定性分析

3.1 计算模型及参数

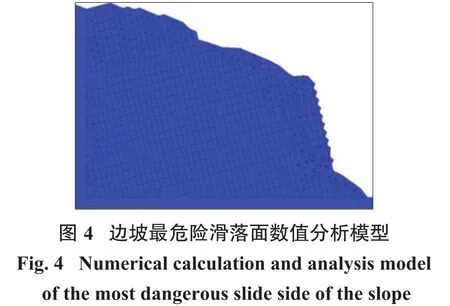
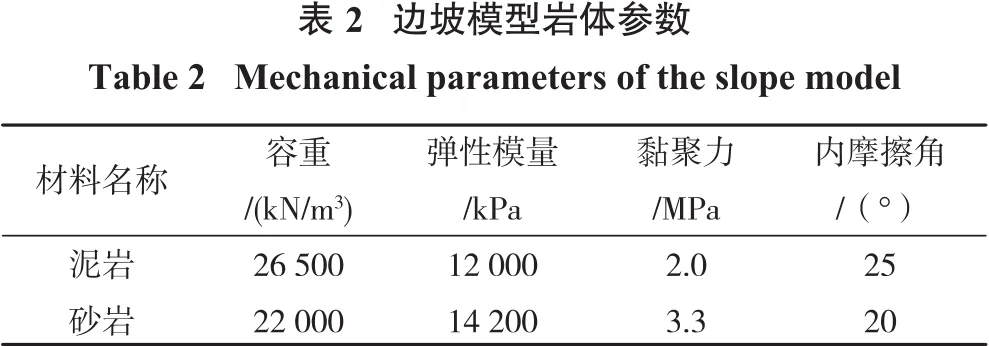
某露天矿边坡基岩裸露（图3），东西宽约200 m，南北宽约160 m，高约150 m，倾角50°～80°。根据地质勘探成果对边坡体进行建模，现场位移监测结果显示该边坡已发生小幅位移，故取最危险滑落面位置二维截面建立数值分析模型，如图4所示，边坡模型岩体参数见表2。

3.2 边坡动态失稳过程

为准确获取滑落面准确位置和对应的安全系数，对该露天矿边坡进行稳定性分析与评价，并对于危险边坡提前采取措施进行治理［21-25］。运用经过理论与经典案例验证的基于动态加速度显式数值流形法程序对该边坡进行动态失稳表征与分析，确定滑落面位置，并给出相应的安全系数，该边坡动态失稳过程如图5所示。

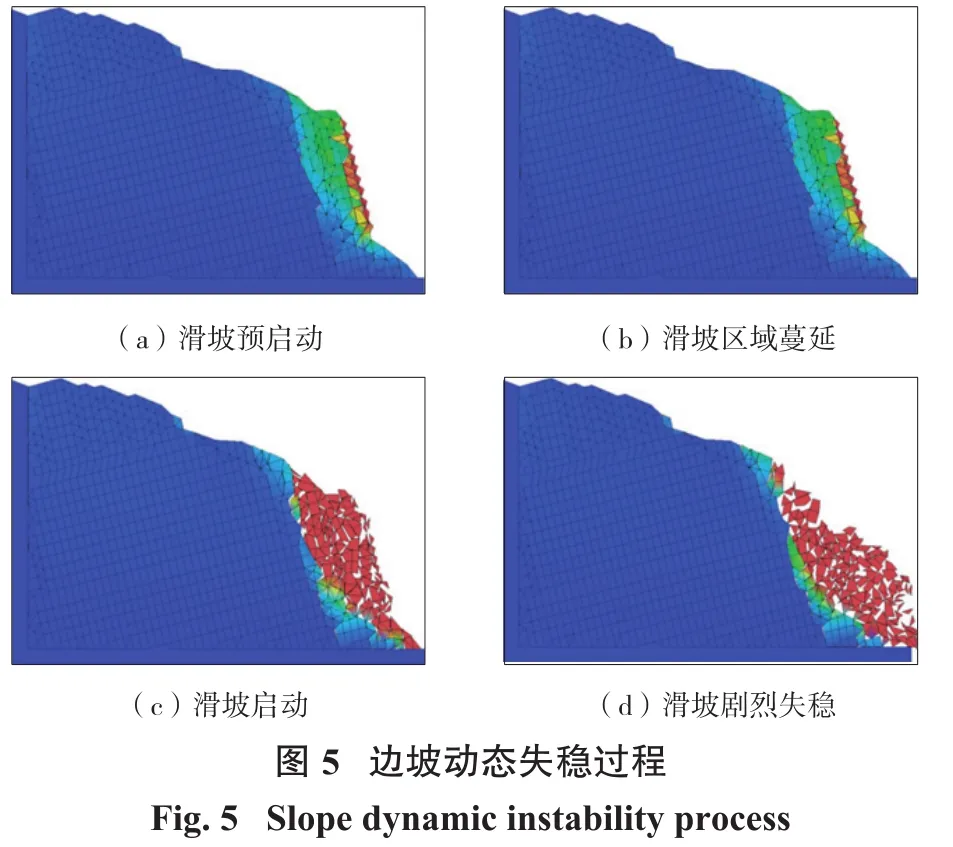
根据图5所示的边坡动态失稳过程，本研究将其分为滑坡预启动、滑坡区域蔓延、滑坡启动、滑坡动态失稳4个过程。滑坡预启动过程出露面岩体出现较大变形，并向内部区域呈不同程度的衰减趋势；滑坡区域蔓延过程出露面岩体变形进一步增大，并进一步影响了内部岩体，导致内部岩体位移也相应达到危险值，动态失稳一触即发；滑坡启动过程中滑坡体变形进一步增大，岩体抗剪强度不足以支撑滑坡体，被迫启动滑坡过程，岩体位移进一步加大，滑坡体势能开始转化为动能；滑坡剧烈失稳过程中滑坡体动能逐步增大，失稳过程达到剧烈程度，上部滑坡体基本与剩余边坡体分离，中下部滑坡体也呈现出剧烈滑动状态，与稳定边坡体区别明显，程序可根据两者特征区别判定出滑动面位置及相应的安全系数。该边坡安全系数为1.174，不满足相关规范规定的安全系数大于1.2的边坡安全条件。

4 边坡治理方案设计及实施

根据边坡动态失稳过程可判断该边坡失稳模式为中上部推移式滑坡，且安全系数较低，存在较大失稳可能。考虑到滑坡体厚度约为30 m，以及滑坡体的实际状况，单纯坡顶削坡及坡脚压载无法从根本上解决问题，可优先采取对滑坡体及失稳面进行注浆加固，增强其自承载能力来提高其稳定性，进而支撑滑坡体后方边坡。

具体实施方式为：边坡内部经管径为60 mm的螺纹注浆管对水泥浆施加适当压力，使得水泥浆渗透进入岩体节理裂隙中，并与松散结构面中介质紧密结合，大大提高结构面黏聚力和内摩擦角，从而提升软弱结构面两侧岩体强度。注浆完毕后，将螺纹注浆管封存在岩体中，借助注浆管实现锚杆加固的效果，同时可旋转螺纹注浆管，产生预应力的作用。坡面布置金属网，并将其与注浆管端部螺母固定，实现边坡整体加固。

该方案实施后，现场边坡监测数据显示块体月累计最大位移不超过0.5 mm，并趋于平缓，从现场统计数据方面印证了该方案的有效性，边坡安全系数由1.174升至安全范围内的1.561，有效保证了该边坡的稳定性。

5 结 论

（1）提出了一种基于动态加速度显式积分算法的NMM，延续了NMM在同一计算架构下处理连续—不连续问题的优势，增强了其处理大规模非线性动力学问题的运算精度。

（2）改进了显式积分算法，并推导了基于动态加速度显式积分算法，测试结果表明当总时步数越多，块体数目越多时，基于该算法的NMM优势越明显，进一步印证了该方法处理大规模非线性动力学问题的可行性及准确性。

（3）基于动态加速度显式数值流形方法，对某露天矿岩质边坡进行了稳定性分析。该边坡失稳模式为中上部推移式滑坡，考虑到滑坡体厚度约为30 m，以及滑坡体的实际状况，采取对滑坡体及失稳面进行注浆加固的方式，有效增强了边坡稳定性。