包含视野参数的聚类目标函数设计

韩 海

（江汉大学 人工智能学院，湖北 武汉 430056）

人工智能在20 世纪90 年代进入了低谷期，新世纪以来，随着计算能力的提高和算法研究的深入，人工智能重新成为科学研究的热门领域。聚类是一种无监督的机器学习方法，是人工智能的基础之一，在统计、图像处理、自然语言理解、经营决策等方面都有广泛应用。聚类是把样本划分成若干个互不相交的子集，每一个子集称为一个“簇”（cluster），使得同一簇内的个体相似度尽可能高，而不同簇内的个体相似度尽可能低。

1 确定簇数的聚类

从实际问题中采集信息，经预处理、规范化之后得到m维空间的测量样本X。设X中共有n个个体，记作每个个体包含m个属性，是一个m维向量，记作对于其中任意两个个体之间的距离表示两者的相似度，通常用欧氏距离表示：

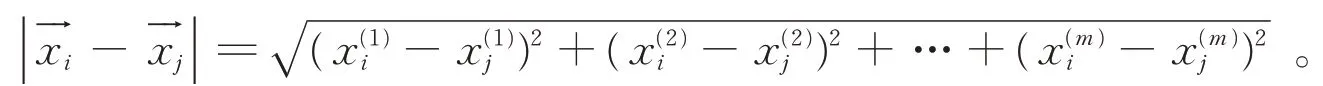
记P是对X进行一次聚类的结果，P把X划分成k个簇，定义每个簇的中心、簇内距离di如下（该定义目前被广泛采用［1−3］）：

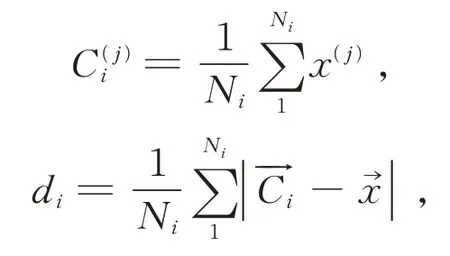
式中，Ni表示第i个簇的容量，x表示第i个簇中的各个个体，1 ≤i≤k。

目前常用的聚类算法有基于均值的K−means 算法、基于密度的DBSCAN 算法等，这些算法在其适用场合都能够对样本进行划分。如K−means 算法就是在预先确定簇数的前提下搜索最佳划分。对于给定的整数k，K−means 算法试图把X聚类成k个簇，使得以下目标函数F(P)的值最小：

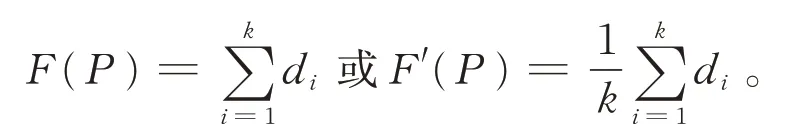
文献［2−3］主要是在搜索的覆盖面上进行改进，调整了选择初始簇心的策略，使得算法能够更好地搜索解空间。对于给定的整数k，K−means 算法及K−means++算法给出的结果往往已接近甚至就是最优解。但是，不论是相关问题的研究［4−7］还是MATLAB、R 语言等提供各类聚类运算工具的平台，都需要以预先确定簇数为前提。在寻找全局最优解时需要人工干预，通常是先人为确定几种可能的k值，对每一种取值进行聚类，将聚类结果进行可视化处理，再人工判定哪一种更好。

2 全局聚类函数

为了进行全自主的聚类，需要设计一种目标函数比较不同k值下的聚类结果。聚类不仅要求同一簇内的个体相似度尽量高，还要求不同簇中的个体相似度尽量低。一个簇中的个体与非该簇的个体相似度通常用簇间距离Di衡量［1，5，8］：

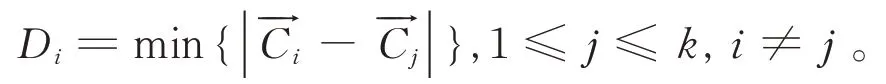
除了针对特定样本的聚类之外，目前还没有能够广泛适用的全局目标函数，仅有较少人对此做过试探［9］。究其原因在于聚类成多少个簇为最优与人的观察有关，针对实际问题的聚类通常没有公认的最优解，比如要把图1 的星云图像划分成若干个星系，不同的人会有不同的看法。本文试图以简单的方式体现人的观察，并把它作为目标函数的一个参数。

综合考虑簇内距离和簇间距离后，设计初始的目标函数G（P）为簇间距离减簇内距离的平均值：

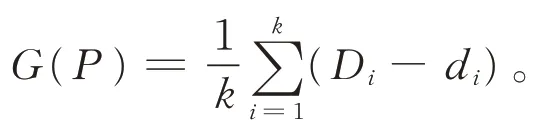
全自主的聚类就是要针对各种可能的k值，找出使得G（P）值最大的划分。实验表明，多数情况下，G（P）的值会随着簇数k的增加而逐渐减小。比如，对图1 所示574 × 329 像点的图像进行采样，按照像点灰度值达到128 为有效点，灰度值每增加16 则重复次数加1（相当于该亮点的权重），得到含2 667 个亮点的数据集，如图2 所示，颜色越深代表重复次数越高，即原图中该像点亮度越高。

图1 星云图像Fig.1 Nebula image

图2 对图1 采样得到的样本Fig.2 The sample obtained by figure 1

用K−means 聚类方法反复实验，得到聚类成2 ～ 13 个簇时目标函数G（P）的最大值见表1第一行。

表1 目标函数在簇数k 为2～13 时的最大值Tab.1 The maximum value of the objective function when the number of clusters k is 2～13

G（P）在k=2 时取得最大值，并且随着簇数k的增加而逐渐减小，如图3 中的实线所示。用其他样本进行实验可以获得类似的结果，表明G（P）总体上呈现出递减的特点，文献［1，8］设计的目标函数也有类似的现象，在不添加限制条件时目标函数总体上表现为单调函数。简单地用G（P）作为目标函数不能合理地表现不同簇数聚类结果的优劣。图3 中的虚线表现的是预期的目标函数的特征(由表1 中第二行数据得到，即加入视野参数后目标函数在簇数k为2 ～13 时变化曲线)，好的目标函数能够在中间适当位置取得最大值而不是单调的。

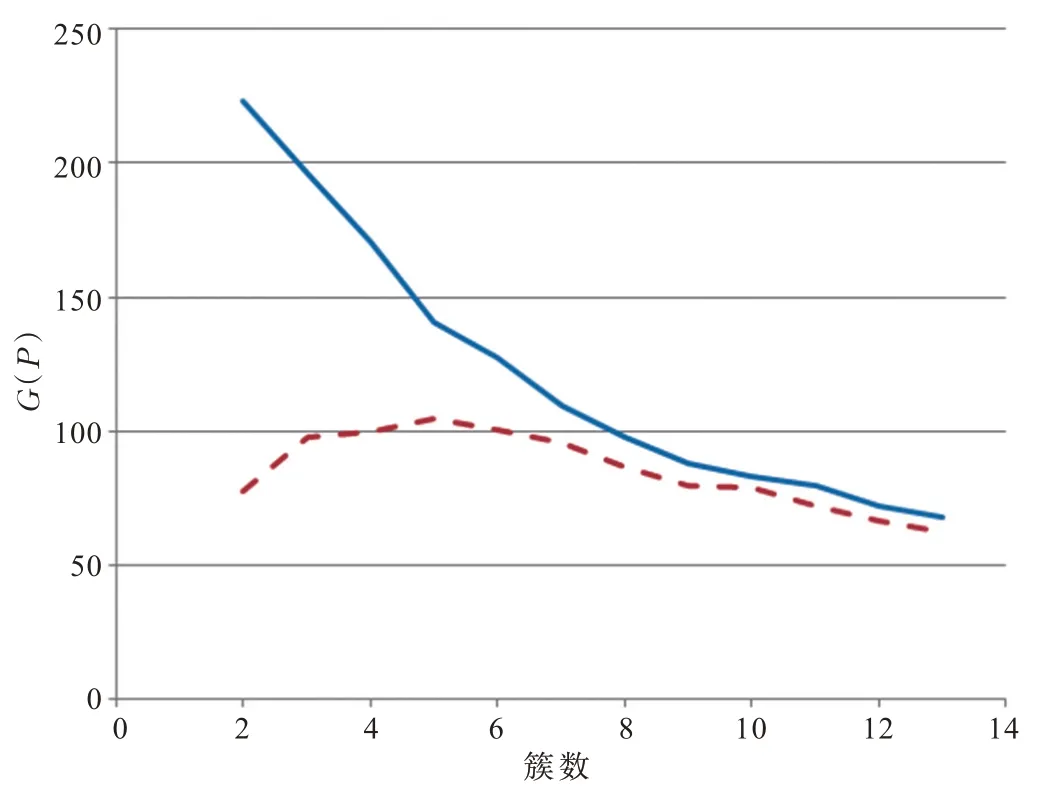
图3 G（P）函数及预期的目标函数Fig.3 G（P）function and expected objective function

3 聚类函数中的视野参数

对于同一个样本，目前尚无成熟的方法用于比较两个簇数不同的聚类的优劣，通常是把簇数不同的聚类结果进行可视化处理之后再由人通过观察来确定。人们通常倾向于把图1 划分成5 ～7 个簇，而把图4 划分成2 ～ 4 个簇。图4 不过是把图1 缩小并在四周添加背景颜色的边框得到，针对两图的不同聚类意向主要来自于视野范围不同。可见，划分成几个簇与人的观察有关，视野是描述观察情况的一种简单方法，在目标函数中加入视野参数是一种可以考虑的设计。

图4 加上广阔背景的星云图Fig.4 Nebula image with a broad background

视野表示人观察事物的粗细程度。定义视野参数是一个数值T，T值越大越趋于大范围宏观观察，T值越小越趋于微观观察。为了使得T能够自适应于不同的样本，可以把该值设计为与样本特征有关的函数。本文把T设计为样本各分量最大差值的线性函数。对于m维样本，记R(1)，R(2)，…，R(m)是各分量的最大差值，Rmin是各个R(t)的最小值：

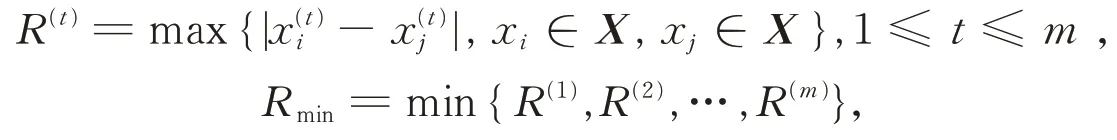
则T可设置为Rmin的线性函数：

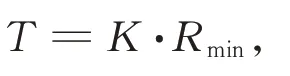
式中，K是定值，针对不同的样本，根据经验，K取值0.3 ～ 0.5 较好。在计算簇间距离时，用T限定Di的上限。先针对某一划分计算出第i号簇与其他簇的簇心之间的距离，令Di取其最小值但不得超过T：

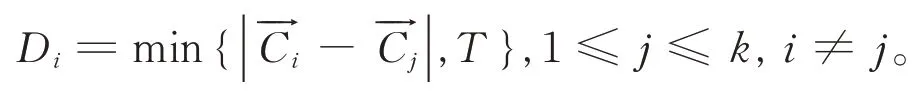
比如，对于图2 所示样本，每个个体有两个属性，x坐标值和y坐标值，其中x坐标的最大差值为原图像的宽度574，y坐标的最大差值为原图像的高度329，取K= 0.4，则T= 131.6。记对簇间距离Di设置上限之后的目标函数为GK(P)，在K取值为0.4 时记作GK=0.4(P)。对图2 的样本进行聚类的结果见表1 的第2 行。GK=0.4(P)在k=5 时取得最大值，此时的聚类结果如图5所示。

图5 用GK=0.4（P）找到的最优划分(k=5)Fig.5 The optimal partition with GK=0.4（P）(k=5)

图5 中的“o”表示各个中心的初始位置，然后根据每个个体到各个“o”的距离指派到离它最近的一个“o”所代表的簇，得到对样本的一个划分。计算当前划分下各个簇的中心，图中用“+”表示。观察图1 可以发现图5 是对原始图像很好的划分。特别的是，如果以图5 中的“+”作为新的初始中心再重新做一次指派，计算得到的目标函数值略小于图5 情况下的结果。

另外，根据添加视野参数后的GK=0.4(P)寻找最优解时，表1 表示的k的各种取值情况下的局部最优解都可以把图1 中明显的两团星云的主要部分划分在同一个簇中。

如果视野参数T取比较小的值，对应于人的主观意愿是把样本划分成更小、更多的簇。表1的第3 行给出了GK=0.2(P)的实验数据，此时T= 65.8。GK=0.2(P)在k= 11 时取得最大值，对应的聚类结果如图6 所示。对样本进行划分时各个初始中心较好地散布在相互距离适中的位置，不足之处是没有突显出两大团星云。

图6 用GK=0.2（P）找到的最优划分(k=11)Fig.6 The optimal partition with GK=0.2（P）(k=11)

针对综合簇内距离和簇间距离的聚类目标函数GK(P)，K−means 算法是用随机的方式寻找最优解的一种方法，但最优解可能出现在算法的某一次循环中，而不一定是算法收敛时的划分。表1 的数据都是通过记载并比较每一轮的划分情况，保留GK(P)最大值而获得。

4 改进的方向

加入视野参数的目标函数GK(P)可以从一定程度上反映人类对于聚类问题的主观意愿，可以比较簇数不同时哪一种聚类结果更好，并具有一定的普适性。极端情况下，目标函数GK=0(P)退化成只考虑簇内距离平均值，GK=+∞(P)就是不考虑视野参数的G(P)。

针对图2 的样本，在实验过程中曾经获得过一个GK=0.4(P)值略低于表1 最大值的划分，如图7 所示，该划分的GK=0.4(P)值为100.7，即表1 中k= 6 的情况。一般来说，人们会倾向于图7 是更好的聚类结果。

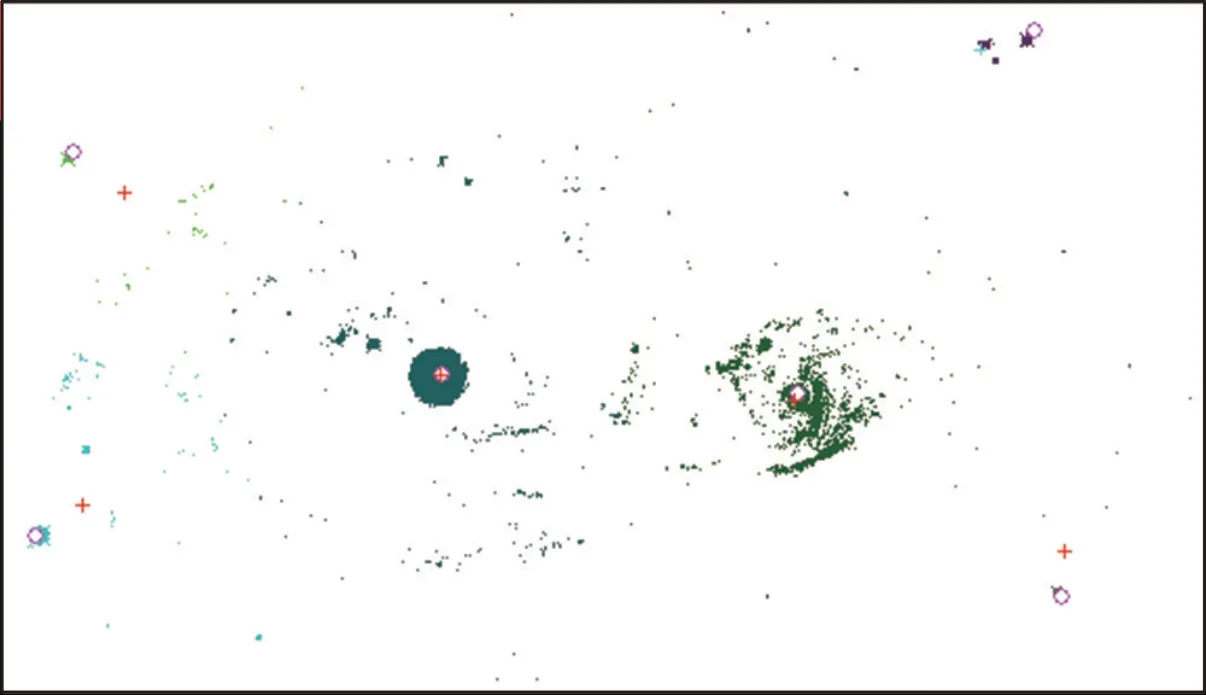
图 7 用GK=0.4（P）在 k=6 时的最优划分Fig.7 The optimal partition with GK=0.4（P）(k=6)

造成图5 的GK=0.4(P)值最大的原因在于该划分中位于左上角的那个簇只有很少的个体，从而导致其簇内距离di很小；而认为图7 更好是因为各个簇比较均衡，簇内距离di相差不大。因此，作为对设计全局目标函数GK(P)的进一步改进，还可以考虑添加表示各簇均衡程度的参数。图5 的划分把图像中部少量本该属于左侧星系的亮点划归到右侧，这是由于按照个体到初始中心点的欧式距离划分它归属于哪一个簇而造成的，改进的另一个方向是寻找更好的划分标准。