约束条件下固定边界系统最优控制必要条件的研究
吴群妹
(无锡科技职业学院 基础部,江苏 无锡 214028)
最优控制理论是现代控制理论的重要组成部分[1−2],国内外有关最优控制的研究已经有很多,如文献[3−4]介绍了一类退化半线性椭圆系统最优控制的必要条件,文献[5−6]研究了有分布参数系统的最优控制,文献[7]研究了固定边界条件下最优控制的必要条件等。用变分法来解决系统的最优控制问题也早已有研究[8−9]。本文研究在固定边界条件下受条件约束的控制问题,利用古典变分法原理,通过构造辅助函数的方法,将有条件约束的系统转化为无条件约束的最优控制问题,再根据拉格朗日方程给出系统达到最优的必要条件及其证明,旨在为受条件约束的固定边界系统最优性能指标的求解提供参考。
1 变分法基本引理
引理1[10]设泛函则

引理 2[10]设其中F为x,y和y'的函数,且F(x,y,y')是三阶可微的,y(x)的边界是固定不变的,且y(x1)=y1,y(x2)=y2,则J取得极值的必要条件是
该方程为著名的欧拉方程,也称为欧拉−拉格朗日方程。
2 约束条件下系统的最优控制
系统的最优控制问题即求其在约束条件下的极值问题,以下给出含3 类不同约束条件的系统状态方程及其性能指标,利用拉格朗日乘数法,将约束条件的极值问题转化为与之等价的无条件极值问题。
2.1 整型约束条件的最优控制
设状态方程的一般形式为

边界条件yj(x1)=aj,yj(x2)=bj,其中yj(x)(j= 1,2,…,n)为状态变量,u(x)为控制输入,约束条件为

ϕi(x)(i= 1,2,…,m)是相互独立的,性能指标表达式为
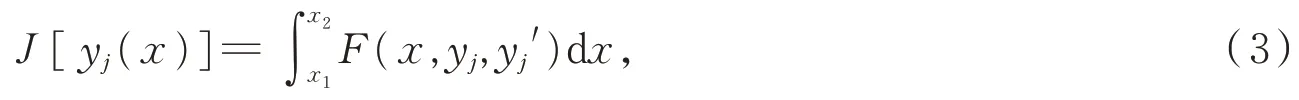
构造辅助函数λi(x)(i= 1,2,…,m;m 此时系统达到最优的必要条件为 其中λi(x)为m个任意的待定函数,根据欧拉方程可解出λi(x)以及状态变量yj(x)。 证明由引理1 可先求性能指标J[yj(x)]的变分,又固定边界条件把每个括号里的第二项运用分部积分法,得 因为变量yj由约束条件(2)式联系着,所以δyj不全是独立的。用λi(x)乘以(2)式并在区间[x1,x2]上积分,得 对(7)式求变分,得 由于λi(x)(i= 1,2,…,m)是m个任意待定的函数,故可假定它由下面m个线性方程即 来决定。这里假定ϕi(x)(i= 1,2,…,m)是相互独立的,即至少要有一个m阶函数行列式不为则可由(10)式求得λi(x)的解。此时(9)式中剩下的变分项只有δy(m+ 1),δy(m+ 2),…,δyn,共(n−m)项,即 这里的每项都是独立的,根据引理2 可得 将式(10)和式(12)合并,即可得到(5)式。证毕。 非整型约束条件通常有微分型约束条件和积分型约束条件。状态方程为(1)式,性能指标为(3)式。 微分型约束条件为 积分型约束条件为 则系统达到最优的必要条件为 证明微分型约束条件下最优性能指标必要条件的证明与整形约束条件下的证明方法类似,在此从略。下面证明积分型约束条件下性能指标达到最优的必要条件。 令 对(16)式两边求导,得 于是约束条件(14)式就可以用(17)式来代替,即问题转化为性能指标在(17)式下的最优问题。引入常函数λi(x),化性能指标为 其中i= 1,2,…,m,m 本文给出3 类受不同条件约束下系统最优控制的必要条件及其证明,旨在为受其他条件约束的自然科学或工程技术中的系统性能指标的计算提供参考。但本文讨论的约束条件下系统达到最优控制是在固定边界条件下的,今后可对可动边界条件的同类系统作进一步探讨。
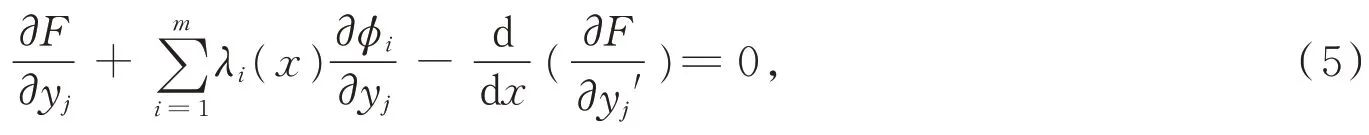






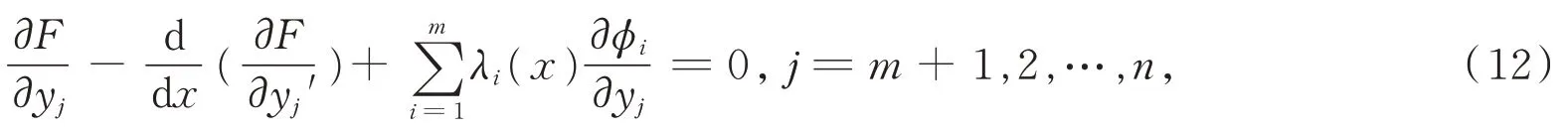
2.2 非整型约束条件的最优控制


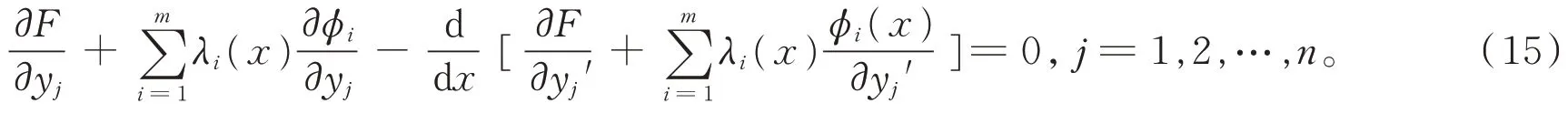


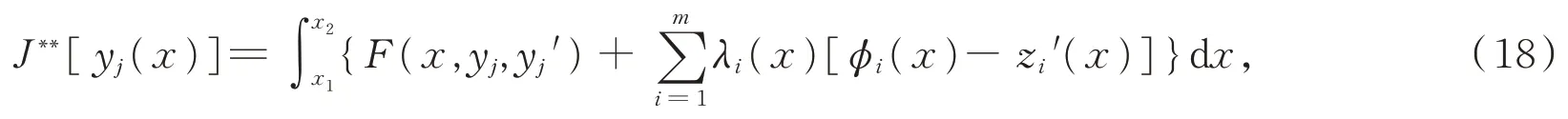
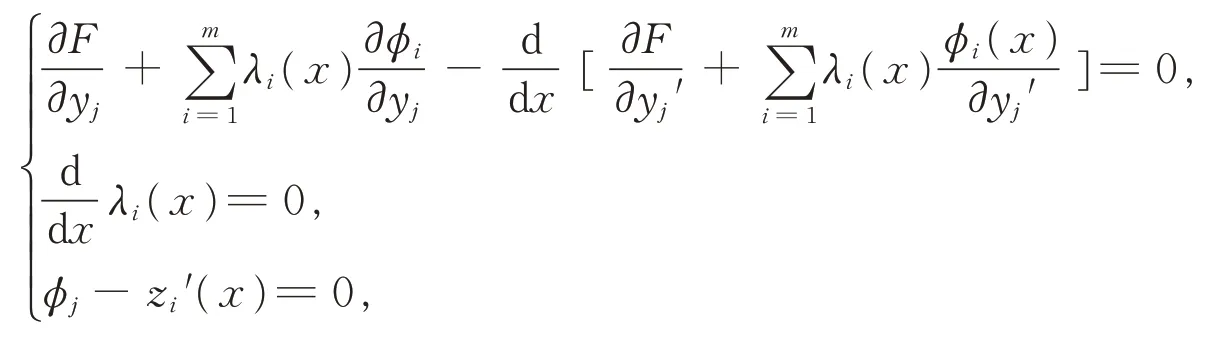
3 结语

