环的局部化条件及应用

李艳午

（芜湖职业技术学院 基础教学部，安徽 芜湖 241003）

0 引言

设R是一个交换的含幺环，如果R有唯一的极大理想，那么称R为局部环[1]，如一个域上的形式幂级数环和任意含幺可换环在素理想上的局部化环均是局部环。

在交换代数中，局部环是一个很普及的概念，因为利用局部化的技术往往可以将问题转化到局部环上，从而交换代数的许多概念和结果往往都落在局部环的框架内。所以，无论是在代数几何中还是对于环论本身，局部环都是一个有力的工具。这使得局部环的概念自提出以来，一直吸引着众多代数学者的研究兴趣。特别是近几十年来，随着同调代数的兴起，局部环的同调性质成为代数K−理论方向一个有意思的对象，文献［2−4］均研究了局部环的同调性质。

本文首先探索了从环的不可逆元的幂零性和理想格的链条件等方面实现环的局部化，在此基础上研究了这些环的性质；其次，研究了SF 环的若干局部化条件，得到了这类环在局部化条件下的一些新结果。

如无特别说明，本文中的环都是可交换的含幺环，相关数学符号的涵义参考文献［2−4］。

1 局部化条件

首先，利用环中非可逆元的幂零性构造环的局部化条件，并由此给出局部环条件下这类环的一个同调性质。

定理1设R是非零环，如果对任意的a∉U(R),存在n∈N，使得an= 0（即a是幂零元），那么ϕ:K0R≅Z,ϕ([R])= 1。

证明如果R是非零环，并且R的非可逆元都是幂零的，那么R/U(R)=J(R)，于是根据文献［5］定理19.1 中局部环的刻画定理，可知环R是局部环。

令f:R→J(R),f(x)=xˉ, 则 kerϕ⊆J(R)。从而，K0f:K0R→K0(R/R(J))是一个单同态。根据文献［4］的例 1.2.3，存在φ:K0(R/R(J)) ≅Z,φ([R/J(R)]) = 1。于是，有单同态ϕ=φ⋅(K0f):K0R→Z,ϕ([R])= 1。ϕ显然是一个满射，从而ϕ:K0R≅Z,ϕ([R])= 1。

定理2设R是可换环，如果R的理想格是一个链，那么有以下结论：

1）R有唯一的极大理想；

2）R/J(R)是一个除环；

3）R/U(R)是R的一个理想；

4）R/U(R)是一个加法群；

5）由a+b∈U(R)可以推出a∈U(R)或者b∈U(R)；

6）对于a∈R,若a左可逆，则a∈U(R)；

7）R没有非平凡的幂等元。

证明由于R的理想格是一个链，根据文献［1］的EX2.12 中的（1）式可知R是局部环，结论1）～ 5）由文献［5］的定理 19.1 可得。

下面证明结论6）和7）。

若a左 可 逆 ，则 存 在b∈R使 得于 是 1 −ba∈J(R),所以ba∈ 1+J(R) ⊆U(R)。从而结论6）成立。

令e2=e∈R,f= 1 −e，则e∈U(R)或f∈U(R)，又 因 为ef=e(1 −e)= 0, 所 以f=0或e= 0，从而结论 7）成立。

将定理1 和定理2 所创造的局部化条件结合起来，就可以得到这两类环的K1群的同调性质。

定理3如果可换环R满足下列条件之一，即

1）R的理想格是一个链；

2）对任意的a∉U(R)，存在n∈ N，使得an= 0。

那么，包含映射：iR×=GL(1,R) →GL(R)导出一个满射

证明分别由定理1 和定理2 可知，当环R满足条件1）或2）时，R都是局部环。假如存在i(1 ≤i≤n),aij∈ radR,j= 1,2,…,n，那么对于任意的矩阵B,都有矩阵AB的第i行元素也都属于radR，因此A没有右逆。同理，假如存在j(1 ≤j≤n),aij∈ radR,i= 1,2,…,n，那么对于任意的矩阵B，都有矩阵BA的第j列元素也属于radR，因此A没有左逆。这说明如果矩阵A的行或者列的元素都属于radR，那么A不可逆。由于在局部环中radR是由不可逆元组成的，所以对于任意的A=(aij) ∈GL(n,R)，每一行、每一列必然至少有一个可逆元。从而对于任意的矩阵A=(aij) ∈GL(n,R)，都可以经过初等行变换变成一个对角矩阵的形式diag [a,1,…,1]。最后，由于K1R是阿贝尔群，所以由R×=GL(1,R) →GL(R)导出的映射是 一 个满射。

注意：在条件2）成立的情况下，若R是非交换环，结论依然成立。

根据文献［1］中推论26.7 可知，局部环上的每个投射模都是自由的，反之却不成立，即每个投射模都是自由的环却不一定是局部环。

下面讨论在每个投射R−模自由的前提下，环R成为局部环的条件，进而探讨在这种局部环条件下矩阵环的行列式映射性质。

定理4设R是一个环（不一定可换），如果R满足下列条件之一：

1）每个投射左R−模都是自由的，并且有补最大值和项不可分解的分解；

2）每个有限生成投射左R−模都是自由的，并且有一个补直和项的分解；

3）R(2)=l1(R)⊕l2(R)是补直和项分解。

a）行列式是初等行变换下的不变量；

b）单位矩阵的行列式等于1；

c）设A∈GL(n,R),a∈R×,如果A'=aA，那么 detA'=ϕ(a)⋅detA。

证明首先，根据文献［1］的EX26.3，当环R满足条件1）～ 3）中之一时，R是局部环。然后，对n运用数学归纳法可以证明映射的存在性。最后，根据文献［2］的定理2.2.5，可知映射ϕ满足性质 a）～ c）。

设A∈Mn(R)，如果存在P,Q∈GLn(R)，使得PAQ为对角矩阵，那么称矩阵A可对角化。矩阵的对角化不仅在线性代数中是一个处理二次型等问题的主要工具，而且是处理其他数学分支及物理问题的一个有力工具。例如，在无穷维的Hilbert 空间里，自伴算子的谱分解就是矩阵对角化的推广；刚体的转动惯量作为一个矩阵，可以通过对角化找到惯量主轴和主转动惯量。下面的定理5 则给出局部化条件下，矩阵环上的二次幂等矩阵的可对角化性质。

定理5设D是一个除环，环R⊆D，如果对于任意的d∈D∗，均有d或d−1∈R,那么对任意的A=A2∈Mn(R)，存在Q∈GLn(R)，使得

证明如果R⊆D，并且对于任意的d∈D∗,都有d或d−1∈R,那么对于非零的a,b∈R,由a+b∈U(R)可以推出a−1∈R或者b−1∈R。事实上，假定a+b=1,对于元素c=a−1b∈D运用 假 设 条 件 ，如 果c∈R, 则 有a−1=a−1(a+b)= 1 +c∈R；如 果c∉R, 则 有c−1=b−1a∈D,于是有b−1=b−1(a+b)= 1 +c−1∈R。故R是局部环。

对 任 意 的A=A2∈Mn(R), 取 幂 等 的 模 同 态ϕ:Rn→Rn。 令P= Imϕ, 则 有 正 合 列0 → kerϕ→Rn→P→ 0。再取嵌入同态：ψ:P→Rn, 由ϕψ= 1, 可知上面的正合列可裂，从而Rn≅P⊕kerϕ，所以A=Mat(P)。再由局部环上模的投射自由性，可知P是有限生成自由R−模。最后，根据文献［4］的引理4.1.19 可知，存在可逆矩阵Q，使得即

2 局部化条件的应用

环R称为置换环[6]，如果对任意的a∈R,存在e2=e∈R,使得e∈aR,1 −e∈ (1 −a)R。显然，局部环都是置换环，而根据文献［7］可知，反之不真。文献［8］研究了局部环的上同调性质，受此启发，下面的定理6 将从置换环的内直和特征对局部环进行刻画，并研究局部环在内直和刻画下K1群的同调性质。

定理6如果环R满足下列两个条件之一：

1）若R2=A1⊕B1=A2⊕B2且A1≅R≅A2，则存在C1⊆A2使R2=A1⊕C1，或者存 在C2⊆B2使R2=A1⊕C2；

2）若R2=A1⊕B1=A2⊕B2且A1≅R≅A2，则R2=A1⊕A2或R2=A1⊕B2。

那么R是局部环，并且存在一个同构映射

证明如果有条件1）成立，那么设a+b= 1，令

则R2=P⊕Q=M1⊕M2，并且Q≅R≅M1。

综上，a左可逆或b= 1 −a左可逆，从而R是局部环。

根据条件2）容易得到条件1），故在条件2）成立时，R也是局部环。

环R称为左（右）SF 环，如果每个单左（右）R−模都是平坦的[9]，而局部环上的投射模都是自由模，基于平坦模和投射模之间的密切关系，笔者在文献［10］的研究基础上研究了SF 环局部化条件下的一些性质。

定理7设R是可交换SF 环，如果R满足下列条件之一：

1）R的每个极大左理想都是有限生成的；

2）R满足特殊右零化子的降链条件；

3）R是满足主理想升链条件；

4）R是左拟完全环。

那么，有如下结论：

a）每个投射左R−模都是自由的，并且有补最大值和项不可分解的分解；

b）每个有限生成投射左R−模都是自由的，并且有一个补直和项的分解；

c）R(2)=l1(R)⊕l2(R)是补直和项分解。

证明根据文献［10］的定理2.1，可知R满足1）～ 4）中任何一条，R就是局部环。再利用文献［1］的 EX26.3 局部环在投射模自由下的直和分解刻画，可以得到结论 a）、b）、c）。

定理8设环R是可交换的SF 环，如果R满足下列条件之一：

1）R有一个生成子RG是阿丁的；

2）每一个有限生成左R−模是阿丁的；

3）每一个有限生成左R−模是有限余生成的。

那么R满足下列性质：

a）对任意a∈R,存在e∈R和u∈U(R),使得a=e+u；

b）若ax+b= 1,则存在e2=e∈R,使得a+be∈U(R)；

c）对于a1,a2,…,an∈R,若a1+a2+ … +an= 1,则存在正交幂等元e1,e2,…,en∈R，使得ei∈Rai(i= 1,2,…,n)；e1+e2+ …+en=1；

d）对任意的有限生成投射R−模P，存在幂等元e1,e2,…,en∈R，使得

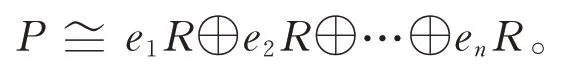
证明首先，根据文献［10］的定理 2.4，可知 SF 环R满足条件 1）～ 3）中之一，R就是局部环，再根据局部环的置换性可得R是置换环。于是，根据文献［6］的命题4.1.1，可得结论a）和b）。

对于结论c），对n利用归纳法。当n= 2 时，由置换环的定义可知结论成立。假设对n=k(k≥ 2)结论成立，设a1+a2+ …+ak+ak+1= 1,则有幂等元e∈R使得e=s(a1+a2+… +ak),1 −e=tak+1,s,t∈R，于是e=esa1e+esa2e+… +esake=e。由于R是置换环，e是幂等元所以eRe 也是置换环。从而，根据归纳假设存在正交幂等元f1,f2,…,fn∈eRe,使得fj∈eResaje（j=1,2,…,k）；并且f1+f2+ … +fk=e。记fi∈eriesaie,ei∈fieriesai, 则有eiej=fieriesai⋅fjerjesaj=fi⋅fjerjesaj, 于 是 当i≠j时 ，eiej= 0；当i=j时 ，ei2=fieriesai=ei。 取ek+1= 1 −e1−e2− … −ek, 则 当i≠k+ 1 时 ，eiek+1=ek+1ei= 0,并 且所 以 ，e1,e2,…,ek+1∈R是正交的幂等元。又因为ej∈Raj(j= 1,2,…,k)，而ek+1e=e−f1− … −fk= 0,从而ek+1=ek+1(1 −e) ∈Rak+1。综上，由归纳假设可知结论c）成立。

对于结论d），假如P是有限生成的投射R−模，那么存在R−模Q和n∈N，使得Rn≅P⊕Q。令e:Rn→P,如果ϕ(x)=(p,q),那么e(x) =p,于是P≅e(Rn)，所以EndR(P) ≅eMn(R)e，即EndR(P)是置换环。令M=P+Q,则

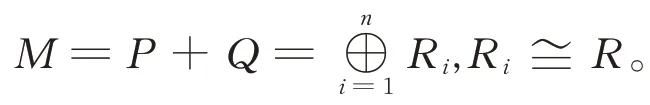
从而存在Qi(1 ≤i≤n)，使得其中Qi分别是Ri的直和项。再令Qi⊕Pi=Ri(i=1,2,…,n)，则有从而P≅P1⊕P2⊕…⊕Pn，其中Pi同构于R的直和项。于是存在幂等元ei，使得Pi≅ei R,进一步地，有结论d）成立。