一些特殊超立方体的Resolvent Estrada指标的研究
2020-12-21 06:04:26乔晓云郑学谦
太原师范学院学报(自然科学版) 2020年4期
乔晓云,郑学谦
(山西大学商务学院,山西 太原 030031)
0 引言

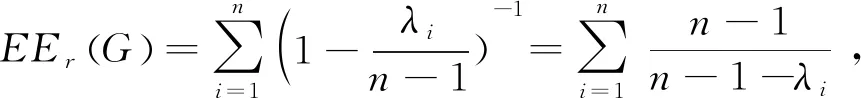
1 超立方体Bn的Resolvent Estrada指标的界
定义1[8]n-维超立方体Bn是一个2n阶的无向图 ,其顶点集:V(Bn)={(x1,x2,…,xn);xi∈{0,1}}.在V(Bn) 中的任意两个顶点相邻当且仅当它们的一个坐标不相同.
引理1[6]对于n-维超立方体Bn,
当n为奇数时,
当n为偶数时,
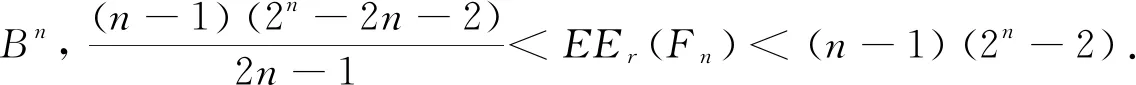
证明 对于n-维超立方体Bn,当n为奇数时,
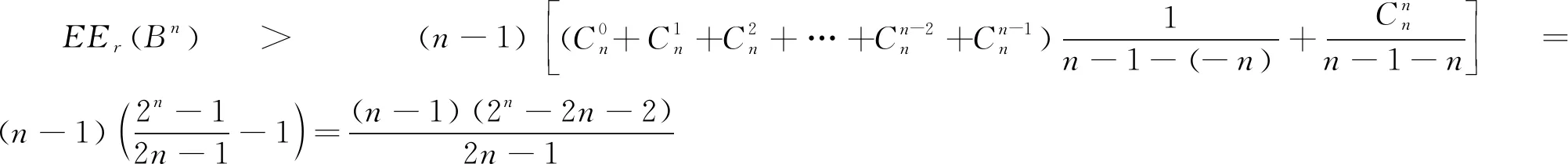
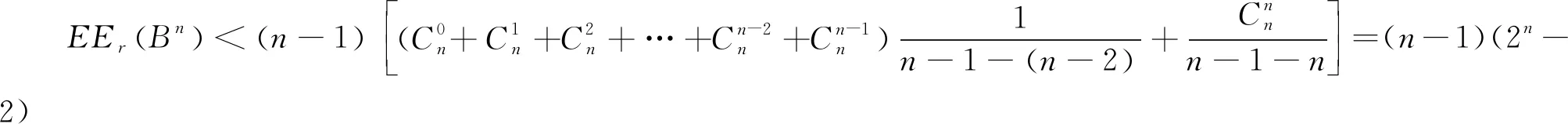
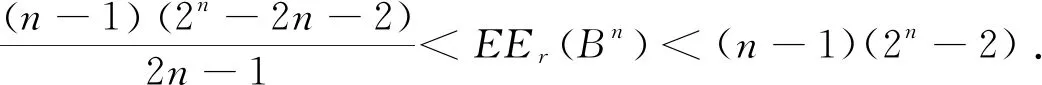
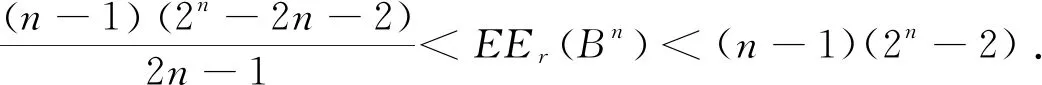
综上所述,定理成立.
2 折叠超立方体 Fn的Resolvent Estrada指标的界
定义2[9]n-维折叠超立方体Fn的顶点集合为:V(Fn)={(x1,x2,…,xn);xi∈{0,1},i=1,2,…,n},顶点x=xnxn-1…x2x1与y=ynyn-1…y2y1有边相连当且仅当满足以下两条其中一条:

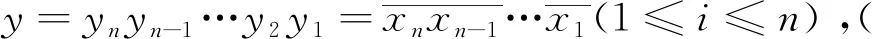
引理2[7]对于折叠立方体Fn,当n为奇数时,
当n为偶数时,
定理2对于折叠立方体Fn,
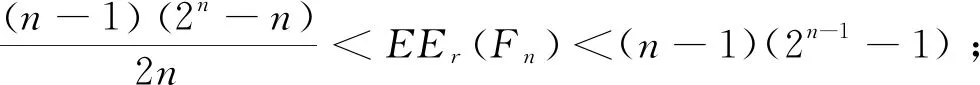

证明 当n为奇数时,
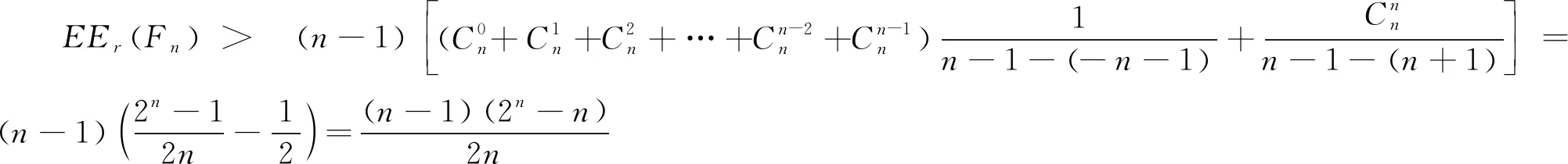



3 增广超立方体Dn的Resolvent Estrada指标的界
定义3[7]n-维增广超立方体Dn的顶点集合为V(Dn)={(x1,x2,…,xn);xi∈{0,1},i=1,2,…,n},顶点x=xnxn-1…x2x1与y=ynyn-1…y2y1有边相连当且仅存在l(1≤l≤n)使得:

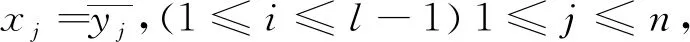
引理3[7]2n-1是n-维增广超立方体Dn的特征值且是最大的.
定理3对于n-维增广超立方体Dn,EEr(Dn)>1-n
证明
引理4当n为偶数时,-n+1是n-维增广超立方体的最小特征值;
当n为奇数时,-n是n-维增广超立方体的最小特征值.
定理4对于n-维增广超立方体Dn,

证明 当n为偶数时,
当n为奇数时,
综上所述,定理成立.
猜你喜欢
科普童话·学霸日记(2023年7期)2023-08-21 09:49:46
小猕猴智力画刊(2021年11期)2021-11-28 21:30:15
小学生学习指导(低年级)(2021年5期)2021-07-21 02:01:04
数学物理学报(2021年1期)2021-03-29 03:13:38
南京大学学报(数学半年刊)(2020年1期)2020-03-19 02:24:44
中学生天地(A版)(2017年6期)2017-06-23 18:32:36
太空探索(2016年9期)2016-07-12 09:59:53
小学生导刊(低年级)(2016年6期)2016-07-02 22:22:15
数学大世界·小学中高年级辅导版(2009年3期)2009-04-14 04:37:58
数学大世界·小学中高年级辅导版(2009年3期)2009-04-14 04:37:58

