求解一类复对称线性方程组的加速MHSS算法

姜 伟，温瑞萍

(太原师范学院 数学系,山西 晋中 030619)

0 引言

复对称但非Hermitian线性方程组的问题：

Ax=b,A∈Cn×n,x,b∈Cn

(1)

求解线性方程组(1)是近年来的热点问题之一,国内外许多学者提出了有效算法.主要有：共轭梯度类方法[1-3]；Krylov类方法[4]；矩阵分裂迭代和预条件迭代类方法[5-8,9,10].其中白中治、Benzi 和陈芳提出的 MHSS[5]及PMHSS[6]迭代法是一种交替格式,非常有效,但其位移参数是根据一些估计预先给定的,在迭代的过程中无论好坏都不曾改变.

文章将基于修正的Hermitian和反Hermitian分裂(MHSS) 迭代法，利用最优化方法自适应动态选择其位移参数[11],提出迭代求解一类复对称但非Hermitian的大型线性方程组的加速MHSS(AMHSS)算法.并给出其收敛结果，最后通过数值实验进行比较来验证算法的有效性.

1 算法及收敛性

本小节给出求解线性方程组(1)的加速MHSS方法如下：

算法(AMHSS算法) 给定精度ε.假设x(0)∈Cn为任意初始值，k=0,1,2,…，直到迭代序列{x(k)}收敛.

1)计算rk=b-Ax(k)；

2)求解线性方程组

(2)

其中αk+1是以下优化问题的解：

(3)

这里rk+1=N(α)M(α)-1rk,而且：

(4)

3) 若‖rk+1‖≤ε，则停止；否则k∶=k+1，返回第一步.

下面考虑算法及收敛性：

引理设{x(k)}是由算法产生的向量序列，M(α)和N(α)由(4)给出，则在第k+1步有:

(5)

其中α是通过优化问题(3)得到的，此外有:

(6)

证明 令φ(α)=(αI-iT)(αI+iT)-1,则有φ(α)*φ(α)=I.

因为：

(αI-W)-1N(α)M(α)-1=(αI-iT)(αI+iT)-1(αI+W)-1=φ(α)(αI+W)-1.

有：

又

故：

定理设A=W+iT∈Cn×n,W∈Rn×n,T∈Rn×n,分别为对称正定矩阵和对称半正定矩阵，α是正常数，迭代序列{x(k)}收敛于(1)的唯一解x*.进一步,若A是正规矩阵,则误差范数‖ek‖=‖x(k)-x*‖2严格递减,即‖ek+1‖2<‖ek‖2.

证明 算法中第k步的误差为‖ek‖=‖x(k)-x*‖2.如果αk+1由(3)得到，则对任意αk>0有:

因此

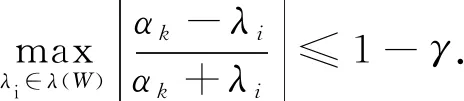
因此：

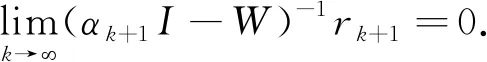
另外，若A是一个正规矩阵，有WT=TW.

因此，迭代矩阵G(α)=(αI+iT)-1(αI-iT)(αI-W)(αI+W)-1也是一个正规矩阵.这表明‖G(α)‖2=ρ(G(α)).

那么，对于T(αk+1)=G(αk+1)G(αk)…G(α1)

有‖T(αk+1)‖2≤‖G(αk+1)‖2‖G(αk)‖2…‖G(α1)‖2=ρ(G(αk+1))…ρ(G(α1))<1.

因此，‖T(αk+1)‖2=‖G(αk)T(αk)‖2<‖T(αk)‖2<1.

所以有，‖ek+1‖2=‖T(αk+1)e0‖2=‖G(αk+1)Tke0‖2<‖Tke0‖2=‖ek‖2.

2 数值实验结果

本小节将通过数值实验来说明新算法的有效性.实验中,迭代次数、运行时间、相对误差及绝对误差分别用“nit”,“tcpu”(单位:s),“Enormr”,“Eres”表示.初始向量x(0)为零向量.且

迭代停止准则为Enormr≤10-6.

问题：考虑下列二维对流扩散方程

-(uxx+uyy)+β(ux+uy)=g(x,y)

在区域(0,1)×(0,1)上满足狄利克雷边界条件，常系数β=i.通过利用五点中心有限差分离散得到复对称但非Hermitian的线性方程组(1)的系数矩阵A=W+iT,并且W=T1⊗I+I⊗T1,T=I⊗V+V⊗I(T1是三对角矩阵T1=tridiag(-1-Re,2,-1+Re)，V=tridiag(2,-1,-1)，h=1/(m+1)是等距步长，网格雷诺数Re=βh/2)，方程组系数矩阵的阶数n=2m.方程组右边b取向量b=Ax*，其中x*=(1,1,…,1)T∈Rn为精确解.

通过采用AMHSS算法求解此问题，对于不同规模的线性方程组求解，所得到的数据结果由表1给出.通过数值结果可以看出，在同样精度下， AMHSS算法在迭代步数和计算时间上都有了明显减少.

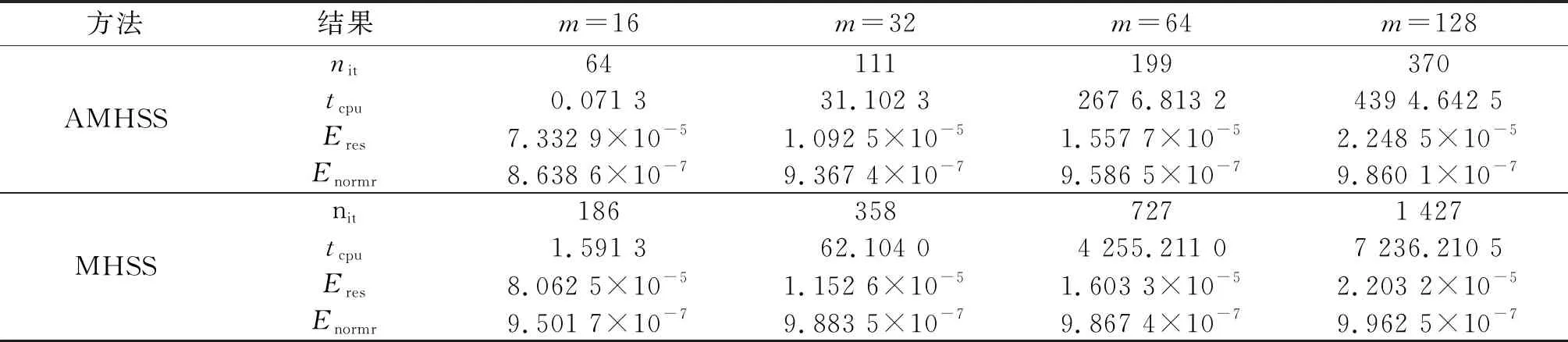
表1 AMHSS和MHSS数值结果的比较

3 总结

在文章中，对一类特殊的复对称但非Hermitian的大型线性方程组的MHSS算法，针对其位移参数α的选择采用最优化方法进行加速研究.并通过实验表明，加速MHSS算法通过选取适当的参数后在计算时间、迭代次数上有明显的缩短，能够更快更精准地进行此类问题的迭代求解.