混合分数Brown运动环境下具有时变参数的再装期权定价
胡倩倩, 周 霞
(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)
1973年Black和Scholes首次提出著名的Black-Scholes(B-S)模型[1]。同年Merton改进了模型假设条件使其更符合实际,建立Black-Scholes-Merton模型[2]。这一研究工作于1997年10月获得诺贝尔经济学奖。Black-Scholes-Merton期权定价模型假设股票价格服从几何Brown运动,然而大量的实证研究表明,股票价格具有长期依赖性和自相似性等特征,这些特征与分数Brown运动的某些特征相符合。于是学者们提出用分数Brown运动驱动的B-S方程代替由标准Brown运动驱动的B-S方程来研究期权定价。
然而当Η≠1/2时,分数Brown运动不是半鞅,直接将分数Brown运动运用于金融市场会产生套利机会[3-4]。为了更好地刻画金融市场,一些学者提出用混合分数Brown运动代替Brown运动。混合分数Brown运动是Brown运动和分数Brown运动的线性组合,它有着与半鞅类似的性质,并且当赫斯特参数Η∈(1/2,1)时,由混合分数Brown运动驱动的金融市场是完备的且无套利[5],从而由混合分数Brown运动驱动的金融市场更具有实际意义。
近年来,混合分数Brown运动下的期权定价问题一直备受学者们的关注。随着金融市场的不断发展,一些标准期权已不再满足市场的需要,于是现实金融市场涌现出了各种各样的新型期权。再装期权与欧式看涨期权不同的是它允许期权的持有者在到期日之前的特定日期执行欧式看涨期权。Johnson等[6]首次给出了标的资产服从标准Brown运动下的再装期权定价公式。由于用分数Brown运动代替标准Brown运动研究资产价格变化更符合实际情况,徐峰等[7]运用Esscher变换的方法提出了分数Brown运动环境下无风险利率分别为常数以及非随机函数的情况下的再装期权的定价公式。传统的期权定价方法对金融市场要求很高,计算过程也比较复杂。1998年Bladt和Rydberg[8]首次运用保险精算方法解决期权定价问题,该方法的优点是其不需要对金融市场做任何经济假设。近年来,有关保险精算方法在再装期权中的应用已经取得了一些理论成果,如何永红等[9]运用保险精算方法研究了分数Brown运动环境下的再装期权,Xu等[10]使用保险精算的方法来估计风险资产在跳-扩散过程下的再装期权。为此,假设股票价格服从混合分数Brown运动,利用保险精算的方法,给出了带时变参数的再装期权定价公式。
1 混合分数Brown运动环境下金融市场模型
假定金融市场由无风险资产(债券)和风险资产(股票)2种资产组成。无风险资产(债券)价格(P(t),t≥0)满足方程
dP(t)=r(t)P(t)dt,
(1)
其中r(t)为无风险利率函数。风险资产(股票)价格(S(t),t≥0)满足方程
dS(t)=μ(t)S(t)dt+σS(t)dBH(t)+
ε(t)S(t)dB(t),
(2)
其中:μ(t)为t时刻的股票价格的期望收益率函数;σ>0为股票价格的波动率;ε(t)为波动率函数;B(t)和BH(t)为定义在完备概率空间(Ω,F,R)上的Brown运动和分数Brown运动,假设二者相互独立。本研究假设赫斯特参数H∈(1/2,1),μ(t)和r(t)均为[0,+∞)→R上的函数,并满足
引理1带时变参数的B-S方程(2)的解为
(3)
证明设V(t)=V(t,S(t)),V(t)为二元可微函数,根据Taylor公式有
因为E[B(t)]2=t,E[BH(t)]2=t2H,所以可近似地认为[dB(t)]2=dt,[dBH(t)]2=2Ht2H-1dt,则有
(dS(t))2=[μ(t)S(t)dt+σS(t)dBH(t)+
ε(t)S(t)dB(t)]2=μ2(t)S2(t)(dt)2+
σ2S2(t)(dBH(t))2+ε2(t)S2(t)(dB(t))2+
2S2(t)[μ(t)σdBH(t)dt+μ(t)ε(t)dB(t)dt+σε(t)dBH(t)dB(t)]=
2Hσ2t2H-1S2(t)dt+ε2(t)S2(t)dt+o(dt)。
忽略高阶无穷小,于是有

(4)
将随机过程V(t)=lnS(t)代入式(4),
σdBH(t)+ε(t)dB(t),
(5)
对式(5)两边取积分得,
证毕。
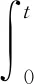
2 混合分数Brown运动环境下带时变参数的再装期权
定义1[10]在到期日T之前只考虑再装一次情况下,再装期权的收益结构为:在再装日期T1(0 当T1→T时,再装期权就退化为欧式看涨期权。 定义2[9]再装期权的保险精算价格定义为 其中I(·)为示性函数。 定理1带时变参数的混合分数Brown运动环境下再装期权保险精算价格为 KN(d4,d5,ρ1)-KN(d1,d3,ρ1)× (6) 计算C1,执行条件为 (7) 由式(3)可得 (8) 将式(8)代入式(7), (9) 对式(9)两边取对数, 因此 令 则 计算C2,由执行条件 -d3, 且 所以 KN(d4,d5,ρ1)-KN(d1,d3,ρ1)× 计算C3,由于 (x<-d1), (z>-d6), 且 E(x,z)=ρ2, 所以 由C=C1+C2+C3,因此式(6)得到证明。 推论1当ε(t)=0,μ(t)=μ,r(t)=r为常数时,式(1)和式(2)退化为 dP(t)=rP(t)dt, (10) dS(t)=μS(t)dt+σS(t)dBH(t), (11) 满足式(10)和式(11)的再装期权定价公式为 C=S(0)N(d2)-Kexp(-rT1)N(d1)+ KN(d4,d5,ρ1)-Kexp(-rT1)N(d1,d3,ρ1)+ S(0)N(-d7,d8,-ρ2)-Kexp(-rT)× N(-d1,d6,-ρ2)。 (12) d7=d1+ρ2σTH,d8=d6+σTH, 运用与定理1相同的方法,可得到推论1的结果,详细证明略。特别地,当ε(t)=0,μ(t)=μ,r(t)=r为常数时,式(12)的再装期权定价公式与文献[9]的定理1一致。 推论2当μ(t)=μ,ε(t)=0,r(t)=r,H=1/2时,式(1)和式(2)退化为 dP(t)=rP(t)dt, (13) dS(t)=μS(t)dt+σS(t)dB(t), (14) 满足式(13)和式(14)的再装期权定价公式为 C=S(0)N(d2)-Kexp(-rT1)N(d1)+ KN(d4,d5,ρ1)-Kexp(-rT1)N(d1,d3,ρ1)+ S(0)N(-d7,d8,-ρ2)- Kexp(-rT)N(-d1,d6,-ρ2)。 (15) 类似于定理1的证明方法,可得到推论2的结果,详细证明略。特别地,当μ(t)=μ,ε(t)=0,r(t)=r,H=1/2时,式(15)的再装期权定价公式与文献[12]的命题一致。 在股票价格遵循混合分数Brown运动驱动的B-S方程的基础上,运用保险精算的方法,推导了混合分数Brown运动下带时变参数的再装期权的定价公式,今后将重点研究如何处理波动率σ=σ(t)的情况。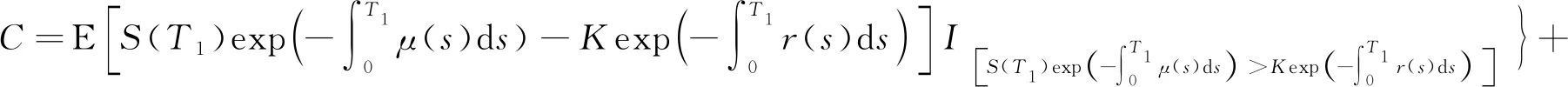


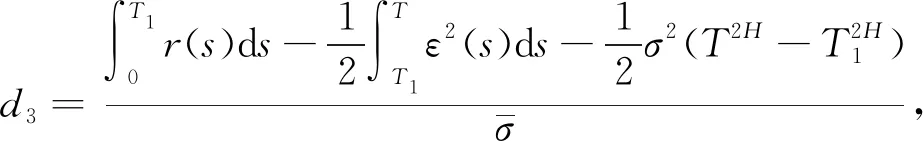

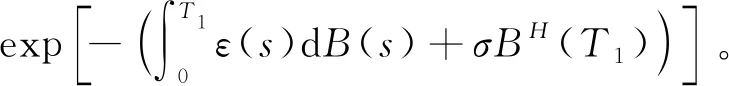



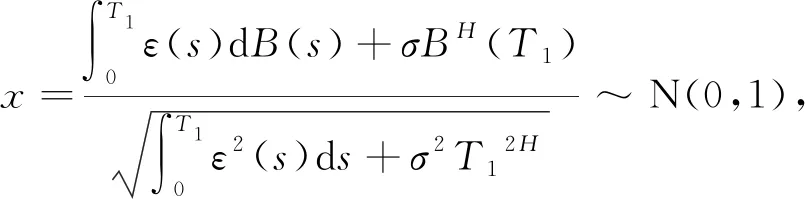

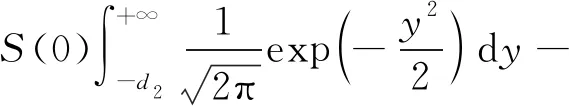

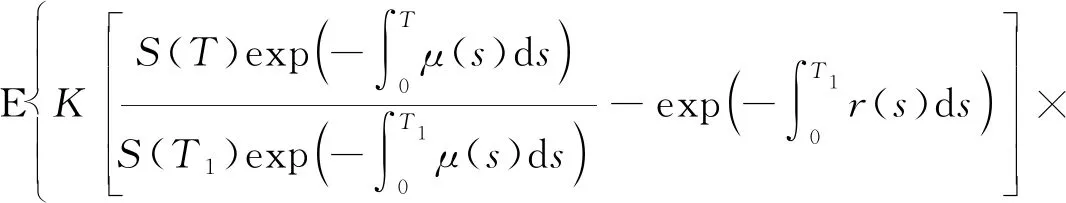
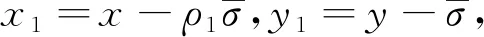
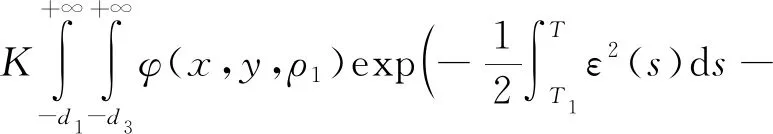





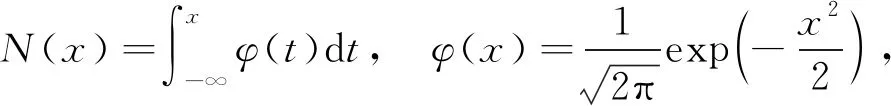
3 结束语

