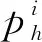一类非线性稳态Poisson-Nernst-Planck方程的有限元方法
刘奕含, 阳 莺,2, 覃柳术
(1.桂林电子科技大学 数学与计算科学学院,广西 桂林 541004;2.桂林电子科技大学 广西高校数据分析与计算重点实验室,广西 桂林 541004)
Poisson-Nernst-Planck(PNP)方程[1]是由Poisson方程和Nernst-Planck(NP)方程耦合而成的非线性偏微分方程,用于描述溶质生物分子体系中移动离子的电扩散,常应用于生物分子[1]、电化学[2]和半导体[3]等相关领域。因PNP方程的非线性性和非对称性,其解析解只在极少数情况下存在,人们提出了各种数值方法求解PNP方程,如有限差分法[4]、有限体积法[5]及有限元法[6]。有限差分法广泛用于求解描述生物离子通道等跨膜孔的电扩散PNP方程[7-8],但将其应用于表面高度不规则的PNP方程时,其精度不高;有限体积法可求解不规则表面的PNP方程,但高精度有限体积控制元的构造较困难;有限元方法可处理边界不规则区域问题,且其解的收敛速度依赖解的正则性。
有限元方法的基本思想是将连续的求解区域离散成有限个且按某些方式连接在一起的单元组合体,利用每一单元内假设的近似函数分片表示求解区域待求的未知函数,将连续的无限自由度问题变成离散的有限自由度问题。为此,利用有限元方法的思想对非线性稳态PNP方程进行离散,提高其求解效率。
1 预备知识
设Ω⊂R3是一个多面体,且满足Lipchitz连续,∂Ω为其边界,使用标准的Sobolev空间记号Ws,p(Ω)及相应的范数和半范数[9],当p=2时,有
Ws,2(Ω)=Hs(Ω),
‖·‖s,p,Ω=‖·‖Ws,p(Ω)。
定义相关的线性有限元空间:
Sh={v∈H1(Ω):v|∂Ω=0∩v|e∈p1(e),
∀e∈Γh(Ω)},

SH={v∈H1(Ω):v|∂Ω=0∩v|e∈p1(e),
∀e∈ΓH(Ω)},
考虑非线性稳态的PNP方程:
(1)
方程(1)的边界满足齐次的Dirichlet边界条件p1=p2=φ=0,其中pi(x)为第i种带电荷量qi的粒子浓度,qi为第i种离子的电荷量,φ(x)为静电势,β=1/(κβT)为逆Boltzmann能量,ε(x)为电介质常量。

c1(pi,v)+d1(pi,φ,v)+f1(pi,v)=
(2)
c2(φ,w)+d2(pi,w)=(F3,w),
(3)
其中,
c1(pi,v)=(pi,v),
d1(pi,φ,v)=(βqipiφ,v),
f1(pi,v)=(f(pi),v),
c2(φ,w)=(εφ,w),
2 有限元方法

(4)
(5)
引理1假设pi∈L∞(Ω),则有
证明
证毕。
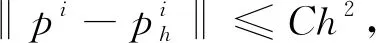
其中C为与h无关的任意常数。
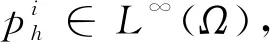

(6)
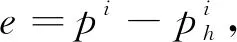
f1(e,vh)=0,
(7)

因此,有

f1(e,pi-vh)-f1(e,e)。
(8)
由引理1及引理2可得,
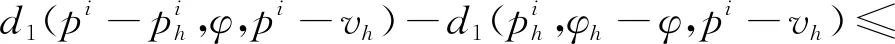
(9)
同理

(10)
其中ε<1。由于f(pi)是Lipchitz连续函数,

(11)

(12)
由式(8)~(12)可得,
因此
记(pi)I=∏hpi,取vh=(pi)I,由插值误差估计有
‖pi-(pi)I‖1,Ω≤Chs。
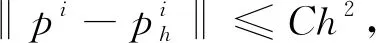
其中C为与h无关的任意常数。证毕。
3 数值实验
求解具有光滑解的非线性稳态PNP方程:
设Ω=[0,1]3,q1=1,q2=-1,边界条件和右端函数依赖于解析解,其中解析解定义为:
表1为H1范数下有限元解和精确解的误差,收敛阶接近1阶,表明有限元法的数值结果与理论一致。
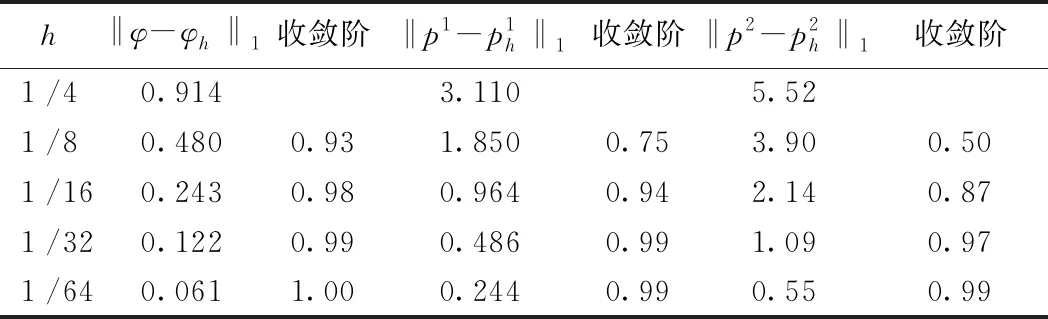
表1 有限元解和精确解在H1范数下的误差
4 结束语