基于过采样和循环平稳的混合OFDM信号子载波数盲估计算法
吴 娟, 谢跃雷, 欧阳缮,2
(1.桂林电子科技大学 广西无线宽带通信与信号处理重点实验室,广西 桂林 541004;2.桂林电子科技大学 卫星导航定位与位置服务国家地方联合工程研究中心,广西 桂林 541004)
正交频分复用(orthogonal frequency division multiplexing,简称OFDM)技术具有较高频谱效率和抗干扰能力,成为数字音视频广播、WiFi及LTE等多种无线传输标准的核心技术,准确估计OFDM子载波数等参数,进而恢复出调制信息,是非合作通信的重要内容之一[1-2]。随着频谱资源的日益紧张,采用LTE-U、eLTE-IOT等技术的非授权频段的设备日益增多,这使得非授权频段的无线电磁环境越来越复杂,而接收信号往往表现为多个OFDM信号时频混迭在一起[3-4],如何有效估计出混合OFDM信号的参数,成为非合作通信的难点之一。
针对单个OFDM信号的子载波数估计研究较多,文献[5-6]分别提出利用倒谱法和基于小波函数的改进倒谱法估计OFDM子载波数,但在低信噪比下性能较差,仅适用于信号质量较高的情况。张政等[7]基于小波函数的改进倒谱法,利用随机共振增强微弱OFDM信号并进行噪声抑制,提高了低信噪比子载波数的估计性能。张海川等[8]提出一种基于OFDM信号自相关矩阵的子载波数估计方法,将接收OFDM信号的自相关矩阵进行特征分解,由特征值的分布特性估计出子载波个数,在高斯白噪声信道和多径信道条件下均可实现对子载波数的有效估计。文献[9-14]证明了OFDM信号在多径衰落信道、高斯白噪声及α稳定分布噪声下,其自相关函数是周期函数,即OFDM信号仍然具有循环平稳特性,进而可利用二阶循环累积量和高阶循环累积量进行子载波数、符号周期及载波频率等多个参数的盲估计。当多个OFDM信号混合在一起时,由于信号间的相互干扰,其信号功率谱特征及循环谱特征与单个OFDM信号存在较大差异,这些单OFDM信号参数的盲估计方法和理论将不再适用。
相较单个OFDM的参数估计,混合OFDM信号的参数估计更加复杂困难,相关研究刚刚起步,目前仅见文献[15]针对同一信道下OFDM多载波混合信号,在衰落及成型滤波参数未知条件下,利用高阶循环累积量,实现对混合OFDM信号的时延参数估计。注意到在非合作通信中信号参数未知,接收端必须采用较高的采样率才能保证信号的完整性,针对具有不同循环前缀的OFDM混合信号,提出一种基于过采样和循环平稳的子载波数估计算法。
1 系统模型及循环平稳特性分析
1.1 系统模型
在实际通信过程中,多径衰落是普遍存在的,因此,混合OFDM信号的数学模型可表示为
r(t)=h1(t)⊗x1(t)+h2(t)⊗x2(t)+w(t),
(1)
其中:x1(t)、x2(t)分别为具有循环前缀且调制参数不同的OFDM信号;h1(t)、h2(t)分别为不同的多径衰落信道;w(t)为高斯白噪声。x1(t)的数学模型为
g(t-kTs)exp[j(2πfct+φ0)],
(2)
其中:cn,k为调制映射的符号序列,它是零均值、独立同分布的;N1为子载波数;L1为循环前缀长度;M1为OFDM符号长度,且满足M1=N1+L1;g(t)为脉冲函数;Ts为码元持续时间;fc为载波频率;φ0为初始相位;k为观察的码元个数。x2(t)的数学模型为
g(t-kTs)exp[j(2πfct+φ0)]。
(3)
1.2 循环平稳特性分析
文献[9-14]已证明了OFDM信号在多径衰落信道、高斯白噪声及α稳定分布噪声下,其自相关函数是周期函数,即OFDM信号具有循环平稳特性。首先分析单个OFDM信号的循环平稳特性,由式(2)得,x1(t)经下变频后可表示为
N1]·g(t-kTs)exp[j(2πΔf1t+φ0)],
(4)
其中Δf1为x1,down(t)信号的残余频偏。于是x1,down(t)的期望表示为
mx1,down(t)=E[x1,down(t)]=
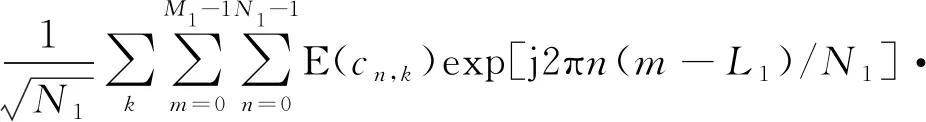
g(t-kTs)exp[j(2πΔf1t+φ0)]。
(5)
因为cn,k是一个MPSK或MQAM信号的调制序列,所以E(cn,k)=0,即
mx1,down(t)=0,
(6)
x1,down(t)的自相关函数表示为

exp[j2πn1(m1-L1)/N1]exp[-j2πn2(m2-
L1)/N1]·g(t-k1Ts)g(t-k2Ts)]·
exp[-j2πn(m1-m2)/N1]·g(t-k1Ts)g·
(t+τ-k2Ts)·exp[j(2πΔf1t+φ0)],
(7)
其中,变量上标*表示某信号的共轭。
(8)
于是式(7)可写成
(t+τ-k2Ts)·exp[j(2πΔf1t+φ0)]。
(9)
由式(7)可知,Rx1,down(t,t+τ)是一个周期为T1的周期函数。由此可知,高斯白噪声信道下单个OFDM信号是一个循环平稳信号。
对于混合OFDM信号,由于各信号分量间相互独立,其数学期望为
mr,down(t)=mx1,down(t)+mx2,down(t)+mw(t)=0,
(10)
自相关函数为
Rr,down(t,t+τ)=E[(x1,down(t)+x2,down(t)+

Rx2,down(t,t+τ)。
(11)
由式(11)可知,Rr,down(t,t+τ)也是一个周期函数,且周期为T1、T2的最小公倍数。于是混合OFDM信号也是一个循环平稳函数。同理可推导出混合OFDM信号在衰落信道下也是一个循环平稳信号,与多普勒频率、传播时延、衰落系数无关。
2 基于过采样和循环平稳估计混合OFDM信号子载波数
本算法基于混合OFDM信号的循环平稳特性,其思路是:根据混合信号的循环自相关序列估计出混合OFDM信号的过采样率,利用过采样后自相关估计出混合OFDM信号的2个有效符号长度,最后估计出混合OFDM信号的子载波数。
若在发射端已经进行了矩形脉冲成型,信道为衰落信道,则接收信号为
r(t)=x1(t)h1(t-kTs)+
x2(t)h2(t-kTs)+w(t)。
(12)
若接收端以q倍过采样,接收信号过采样后为离散信号,则接收信号为
r(n)=x1(n)h1(n-kq)+
x2(n)h2(n-kq)+w(n)。
(13)
由文献[16]可知,过采样后的OFDM混合信号仍具有循环平稳特性,且循环平稳周期为
(14)
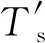
(15)
循环自相关计算公式[9,11]为
(16)
其中α、τ分别为循环频率和时延。对r(t)r*(t-τ)进行FFT变换,
(17)
其中M为运算数据量,k为傅里叶变换的点数。经过上述分析,可得过采样率的估计式为
(18)

(19)
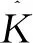
τ=1,2,…,L,i=1,2,
(20)
其中:
L为偏移长度τ的最大取值,Ri(τ)为τ∈[1,L]对应的自相关的值,Ei(τ)为信号能量,Mi为进行参数估计的数据个数。偏移长度一定要大于信号的有效符号长度,这是为了保证算法的有效性。于是混合OFDM信号的子载波数估计为
(21)
本算法步骤为:
1)由式(17)计算混合OFDM信号的循环自相关序列。
2)利用峰值搜索法搜索相邻峰值,估计出循环频率α之间的间隔。
3)利用式(19)估计出采样倍数q。
4)由式(20)估算出混合信号过采样后的自相关序列,用峰值搜索法遍历混合信号信息,寻找第1尖峰和第2尖峰,计算尖峰间隔,从而估计出混合信号的2个有效符号长度。
5)利用式(21)估计出混合OFDM信号的子载波数。
3 实验仿真
仿真条件为先产生混合OFDM信号,其中一个OFDM信号子载波数为128,子载波映射方式为QPSK,循环前缀比例为1/4,另一个OFDM信号子载波数为256,子载波映射方式为16QAM,循环前缀比例为1/4,载频为20 MHz,采样率为40 MHz,过采样率为4,FFT点数为6 144,时延τ=1 μs,信噪比为10 dB。实验验证基于过采样和循环平稳的混合OFDM信号子载波数估计算法的有效性以及采样倍数、子载波数变化对实验估计的影响。


图1 延时为1 μs的循环自相关序列
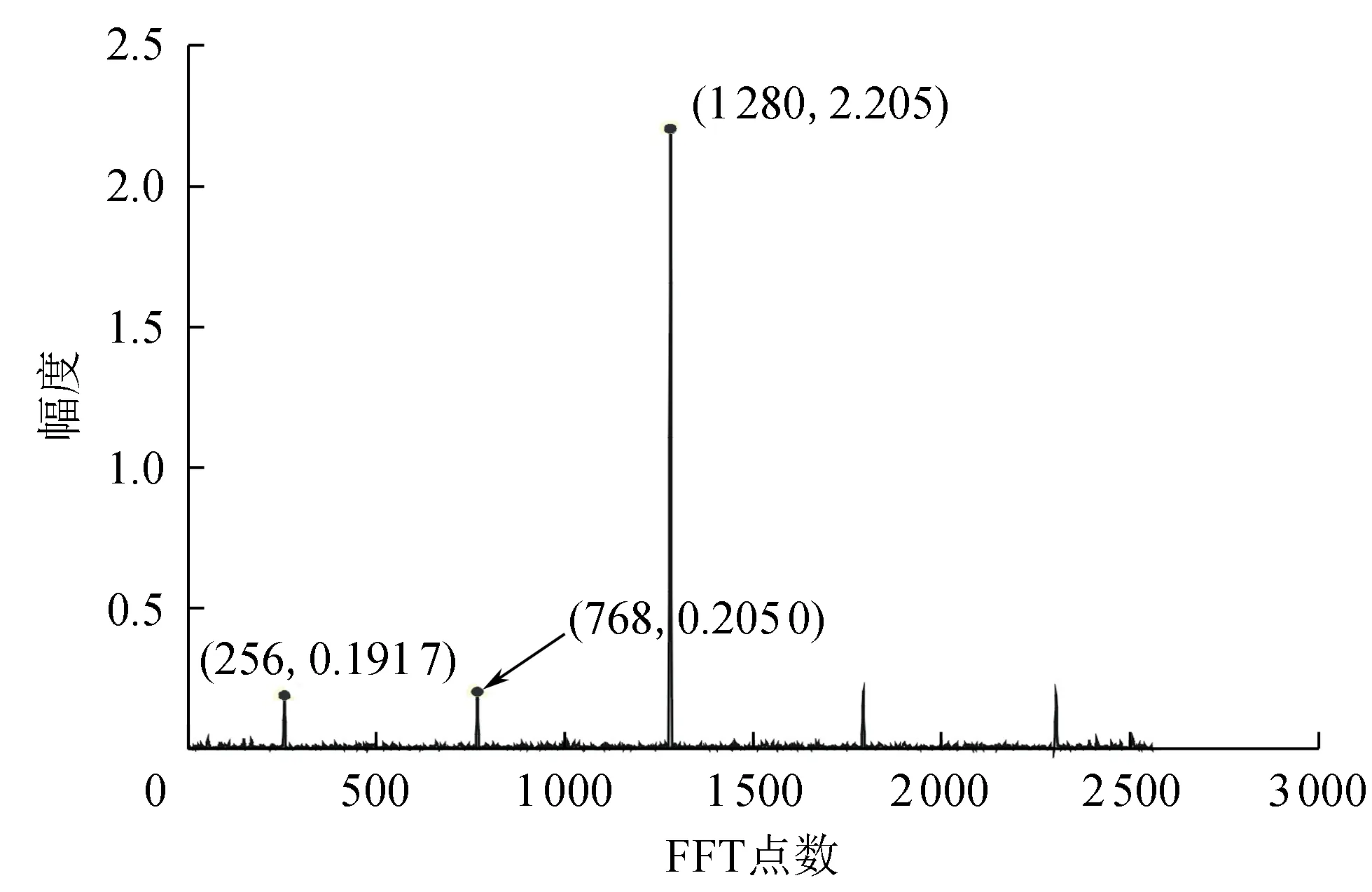
图2 混合OFDM信号有效符号长度估计
2)信道为2个不同的衰落信道,其中一个信道是四径衰落信道,各路延时为0、0.1、0.2、0.3 μs,对应功率为0、-4、-8、-12 dB;另一个信道为六径衰落信道,各路延时为0、0.1、0.2、0.3、0.4、0.5 μs,对应功率为0、-4、-8、-12、-16、-20 dB,最大多普勒频率分别为0、1 611 Hz。计算Rr(n,1)的值,对Rr(n,1)进行FFT变换,得到不同衰落信道下延时为1 μs,fd为0、1 611 Hz的循环自相关序列如图3所示,图4为不同衰落信道下,fd为0、1 611 Hz的混合OFDM信号有效符号长度估计。同实验1)一样,先由图3(a)和图4(a)估计出fd为0、1 611 Hz的混合OFDM信号的循环频率峰值间距离,求出过采样率q,再根据图3(b)和图4(b)估计出fd为0、1 611 Hz的混合OFDM信号的有效符号长度,最后得到混合OFDM信号的子载波数估计。不同衰落信道下也可以估计出子载波数分别为128和256,验证了本算法的有效性。
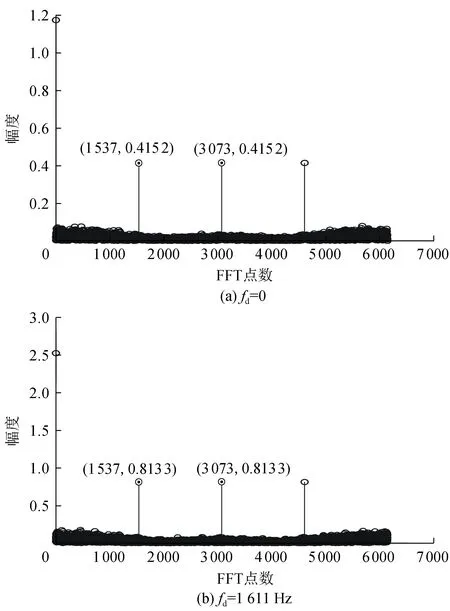
图3 fd=0、1 611 Hz,τ=1 μs循环自相关序列

图4 fd=0、1 611 Hz信号有效符号长度估计
3)验证本算法的性能,信噪比为-5~25 dB,每隔2 dB取一个值,信道分别为高斯白噪声信道和实验2)中的衰落信道,分别做蒙特卡洛仿真实验。图5为子载波数估计性能随信噪比变化的曲线。从图5可看出,低信噪比下,本算法也能准确估计出混合OFDM信号的子载波数,在-1 dB时,算法的正确估计率可达100%。可见,在低信噪比下,本算法在衰落信道中是有效的,且性能良好。

图5 估计性能随信噪比变化的曲线
参数变化对实验的影响:
1)子载波数的变化对实验的影响。仿真参数相同,只改变其中一个OFDM信号的子载波数,即将其中一个OFDM信号的子载波数由256改为1 024。图6为高斯白噪声信道下估计,图7为不同衰落信道fd=0下的估计。从图6、7可看出,子载波数的变化不影响实验估计,仍可准确估计出混合OFDM信号的子载波数。
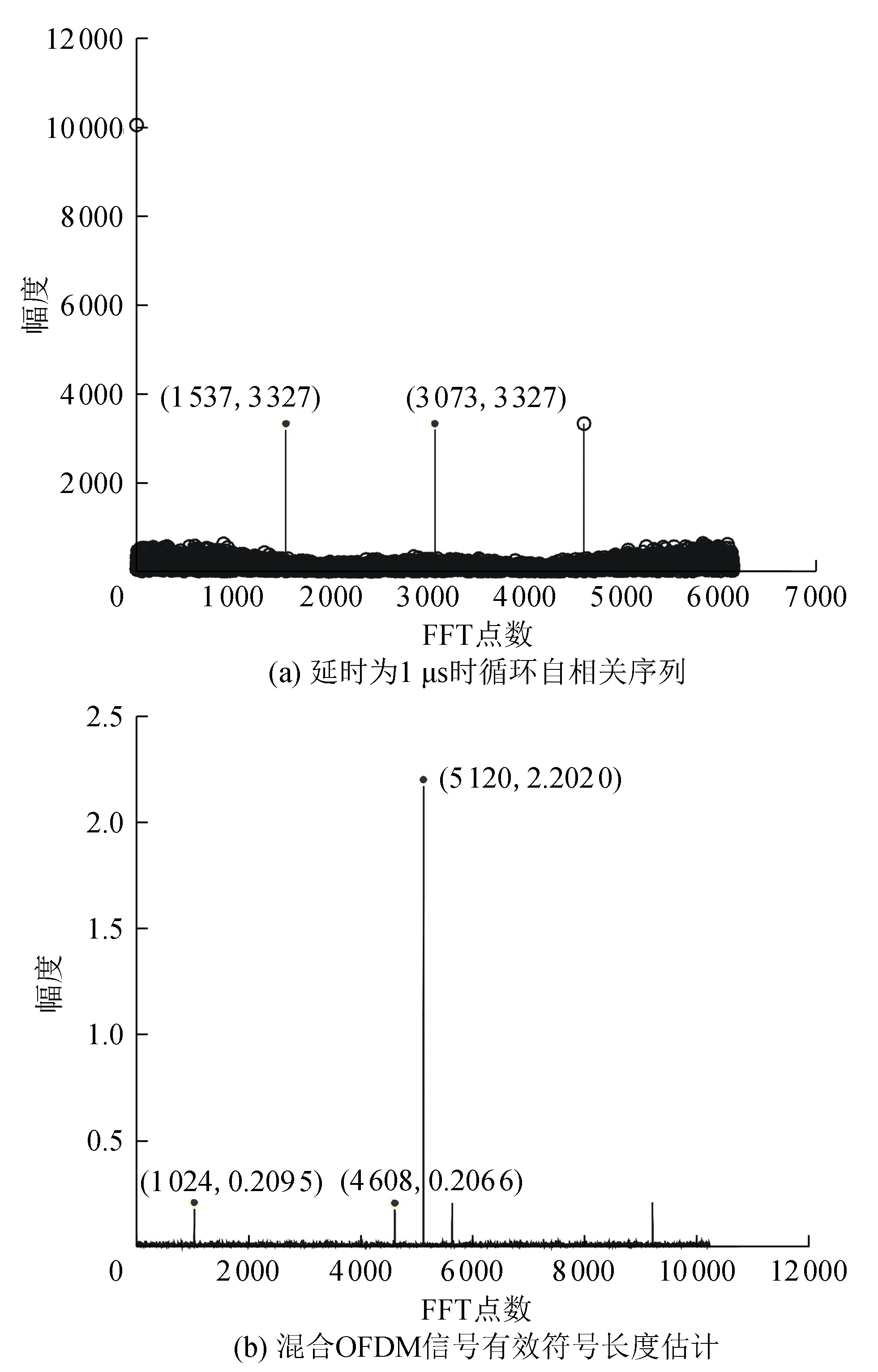
图6 子载波数变化,AWGN下混合OFDM信号的子载波数估计
2)采样倍数的变化对实验的影响。仿真参数相同,只改变采样倍数,即将4倍过采样倍数改为8倍,图8为高斯白噪声信道下的估计,图9为不同衰落信道fd=0下的估计。从图8、9可看出,采样倍数的变化也不影响算法的有效性,仍可以准确估计出混合OFDM信号的子载波数。
3)子载波数和采样倍数同时变化对实验的影响。仿真参数相同,只改变子载波数和采样倍数,即将其中一个OFDM信号的子载波数从256改为1 024,同时将4倍过采样倍数改为8倍,图10为高斯白噪声信道下的估计,图11为不同衰落信道fd=0下的估计。
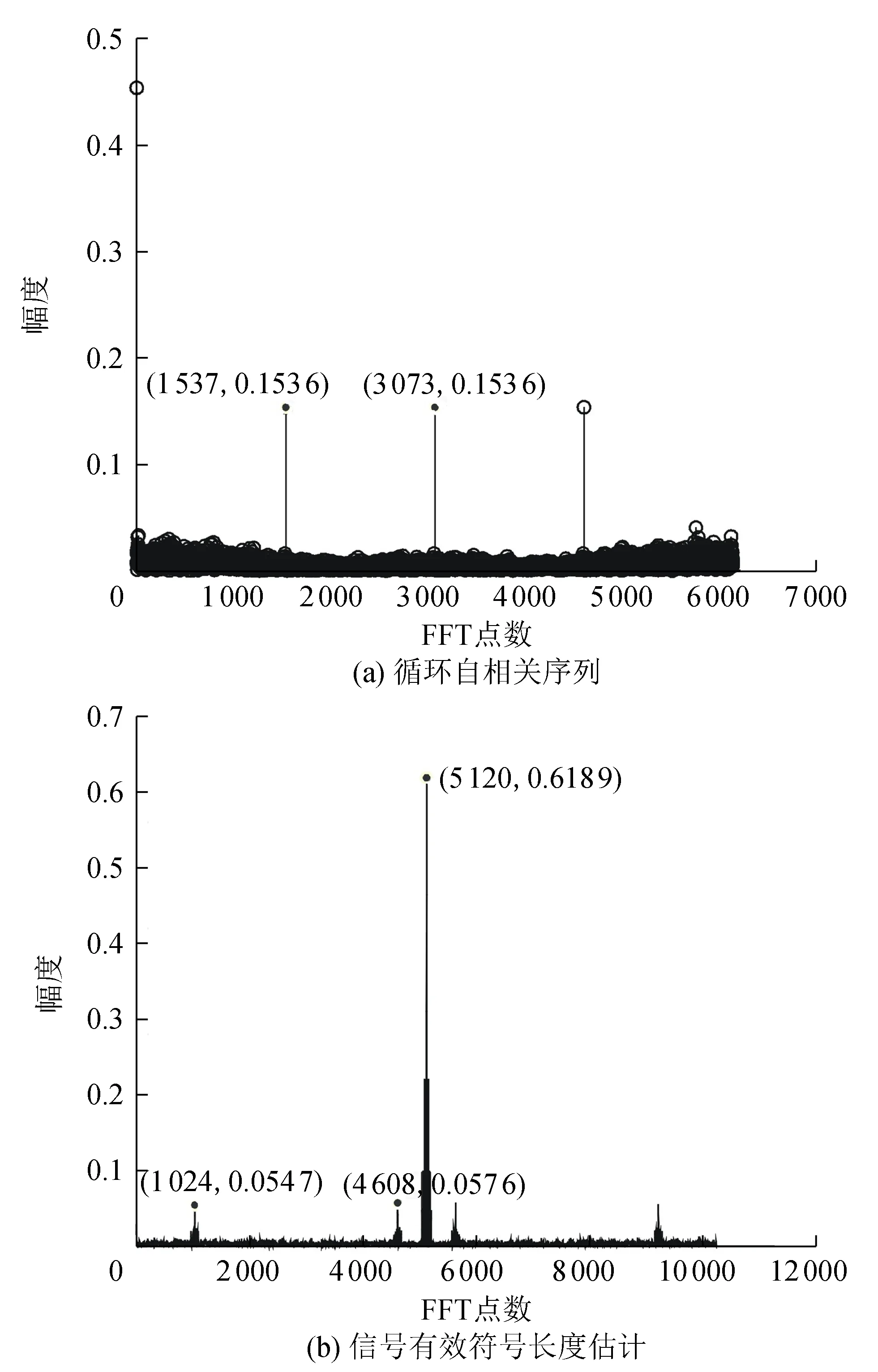
图7 子载波数变化,fd=0时混合OFDM信号的子载波数估计

图8 采样倍数变化,AWGN下混合OFDM信号的子载波数估计
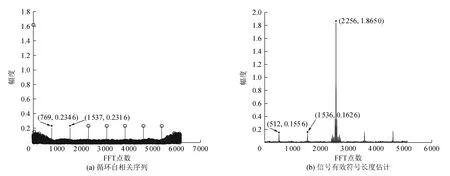
图9 采样倍数变化,fd=0时混合OFDM信号的子载波数估计
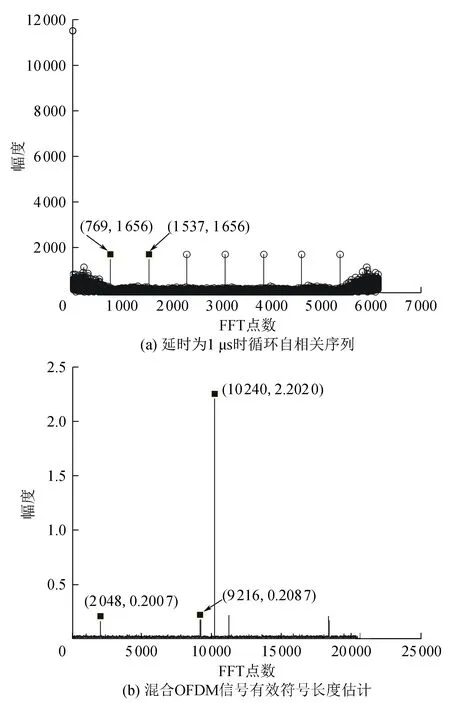
图10 子载波数和采样倍数变化,AWGN下混合OFDM信号的子载波数估计

图11 子载波数和采样倍数变化,fd=0时混合OFDM信号的子载波数估计
从图10、11可看出,本算法也可以准确估计出混合OFDM信号的子载波数。
综上所述,基于过采样和循环平稳的混合OFDM信号的子载波数估计算法是有效的,过采样倍数、子载波数的变化对估计性能并无影响。
4 结束语
在混合信号识别领域,无线电磁环境的日益复杂使得混合信号的识别、解调更加困难。针对混合OFDM信号子载波数估计难的问题,提出了基于过采样和循环平稳的混合OFDM信号子载波估计算法,建立了不同衰落信道下混合OFDM信号模型,证明了混合OFDM信号的循环平稳特性,验证了在低信噪比下,本算法可在不同衰落信道下准确估计出子载波数,同时分析了本算法采样倍数的变化、子载波个数的变化以及两者同时变化对实验的影响,通过验证证明采样倍数、子载波个数等参数的变化并不影响算法的有效性,此外,还通过仿真实验验证了在低信噪比下,本算法在不同衰落信道中具有良好的性能。

