基于遗传算法优化参数的VMD-WVD的无人机微动特征时频分析方法
蔡 宇, 欧阳缮, 廖可非
(桂林电子科技大学 信息与通信学院,广西 桂林 541004)
微动是指目标或目标部件除质心平动以外的振动、转动和加速运动等微小运动。目标的微动会引起雷达回波的频率调制发生变化,该现象称为微多普勒效应[1-2],它描述了微动激励的瞬时多普勒,反映了频率的瞬时特性。无人机是一种“低慢小”目标[3],若能充分利用其旋翼叶片的微动特征[4],将为无人机的检测与识别提供新的思路。由于无人机的微多普勒频移是时变的,而傅里叶变换不能提供时间有关的频率信息,故不适用于微动特征的分析。为了得到与时间有关的频率信息,通常采用联合时频分析[5](time frequency analysis,简称TFR)方法,例如短时傅里叶变换[6]、小波变换[7]等。但是这些线性时频变换受到窗函数的影响,时间分辨率和频率分辨率相互约束,无法同时达到最优。而基于二次时频变换的魏格纳-威尔分布(Wigner-Ville distribute,简称WVD)具有良好的时间边缘特性和频率边缘特性,对解决线性时频变换存在的问题具有明确的物理意义。但WVD方法也存在缺陷,容易受到交叉项的影响,引起时频谱的模糊,这也是它未能得到广泛应用的原因。为了解决这一问题,有学者提出了伪魏格纳-威尔分布、平滑伪魏格纳-威尔分布等方法,它们主要通过以牺牲局部的时频聚集性为代价设计核函数来抑制交叉项。全盛荣等[8]通过构建Gabor原子字典,利用匹配追踪(MP)算法实现信号分解,解决了WVD的交叉项问题,但字典构建是一个难点,且计算量大。为了解决上述问题,提出基于遗传算法优化参数的变分模态分解(variational mode decomposition,简称VMD)与魏格纳-威尔分布的无人机微动特征时频分析方法。
1 方法简介
1.1 Wigner-Ville分布
魏格纳-威尔变换是一种具有高分辨率的二次时频变换。连续时间信号x(t)的WVD实际上是自身的时频能量密度,
(1)

Wx1(t,ω)+Wx2(t,ω)+2Re[Wx1,x2(t,ω]。
(2)
由式(2)可知,WVD除了信号本身的能量外,还多了2Re[Wx1,x2(t,ω]这一项,这是所有二次时频分布的“二次叠加”性质。对于一个有n个分量的信号,每个分量都有一个自分量,每一对信号分量都有一个对应的负分量。因此,信号分量越多,交叉项干扰越严重。交叉项以震荡的形式出现在时频谱中,而信号真正的能量全部在自项中,交叉项对于信号的能量并无贡献。由于交叉项不容易消除,会引起时频谱模糊。
1.2 变分模态分解
变分模态分解[9-10]是一种非递归的变分分解模型的自适应方法,它通过交叉方向乘数迭代模型寻求信号的最优解来确定每个IMF的最优解。VMD实际上是由经典的维纳滤波(Wiener filtering)构成,是自适应性的一种概括形式,对采样和噪声具有更好的鲁棒性。此外,VMD方法可以将2个谐波频率相近的纯谐波信号分离。通过VMD方法,可以将信号分解成若干个中心频率为ωk且具有一定稀疏性的调幅调频的模态函数。第k个模态函数的表达式为
uk(t)=Ak(t)cosφk(t),
(3)
其中:Ak(t)为模态函数的瞬时幅值;φk(t)为相位函数。对相位项的时间求导,可得到模态函数的瞬时频率ωk(t)。相对于相位函数,振幅和频率的变化更加缓慢。因此,在时间间隔[t-Δ,t+Δ]可以将uk(t)视为一个振幅为Ak(t)、瞬时频率为ωk(t)的谐波信号,且Δ≈2π/ωk(t)。分解后的uk(t)重构为原信号,具有特定的稀疏性,uk(t)的频域和带宽决定了其稀疏度。
VMD方法分解模态函数的步骤为:

(4)
(5)
(6)
4)重复步骤2)~3),直到满足迭代终止条件:
(7)
停止分解,其中判别精度ε应大于0。
5)输出k个模态函数。
1.3 遗传算法优化VMD参数原理
利用VMD算法对信号进行分解需要预设分解参数,其中惩罚因子和模态函数个数是对分解结果影响最大的2个参数。通常对信号进行VMD分解时,多是基于经验预设[11],但在工程计算中,信号往往比较复杂,若仅通过经验预设,有可能达不到最优分解的效果。且2个参数是相互影响的,若通过固定其中一个参数来求解另一个参数,也不能得到信号的最优分解。因此,寻求惩罚因子和模态函数个数的最优分解参数是VMD算法的关键。
遗传算法[12](genetic algorithm简称GA)是用于最优解的搜索算法,通过模拟自然进化过程进行最优解求解。该算法的实质是通过种群搜索技术将种群作为一组问题解,通过对初代种群使用生物遗传环境的选择、交叉等操作得到新一代的种群,逐渐将种群优化包含最优解的状态。遗传算法作为一种智能算法,具有全局性,通过适应性函数对目标所在的解空间进行全局搜寻得到最优解,且可同时对多个参数进行优化。
遗传算法优化参数主要包括初始编码、生成初始种群、设置适应度函数、选择、交叉、变异6个步骤。遗传算法优化参数的流程如图1所示。遗传算法通过逐次迭代搜寻,达到参数优化的目的。信号的信息熵是适应度函数。信息熵可作为信号稀疏度的评价指标,熵值越大的信号,不确定性越大,反之则越小。经VMD分解后的信号信息熵即原信号的包络熵,可表征原信号的稀疏度。无人机旋翼的微动信号在发生闪烁时特征明显,表现出较强的稀疏性,包络熵较小。对于含噪声较多的分量,闪烁现象不明显甚至被覆盖,此时信号的稀疏性较弱,包络熵较大。通过遗传算法优化VMD参数,可得到信号最优的稀疏分解。
在对VDM进行参数优化时,遗传算法中的染色体即为待优化的参数(k,α)。参数(k,α)的VMD分解后得到uk,求解uk的包络熵作为染色体优化的适应度函数,其中最小的包络熵为局部极小包络熵,与对应的uk分量构成局部最佳分量组合。通过局部极小包络熵得到的适应度函数,全局搜索得到最小化局部极小包络熵,达到全局最优参数的目的。

图1 遗传算法优化参数流程
1.4 基于遗传算法优化参数的VMD-WVD
VMD不存在模态混叠现象和端点效应,且抗噪性能更好,引进了遗传算法全局搜索,得到最优参数模态个数k和惩罚因子α。通过参数优化的VMD方法,复杂信号可分解为频率不同的纯谐波信号,再将这些频率单一的信号进行WVD变换,可达到减少交叉项的目的。遗传算法参数优化的VMD-WVD特征提取方法实现过程如下:
1)以输入信号的信息熵作为遗传算法的适应度函数,得出信号VDM的全局最优参数(k,α);
2)对雷达回波信号进行VMD,得到k个模态函数分量;
3)对k个模态函数分量分别进行WVD变换;
4)将各模态函数的时频进行线性叠加得到最终的时频分析结果。
遗传算法优化的VMD和WVD的时频分析方法流程如图2所示。
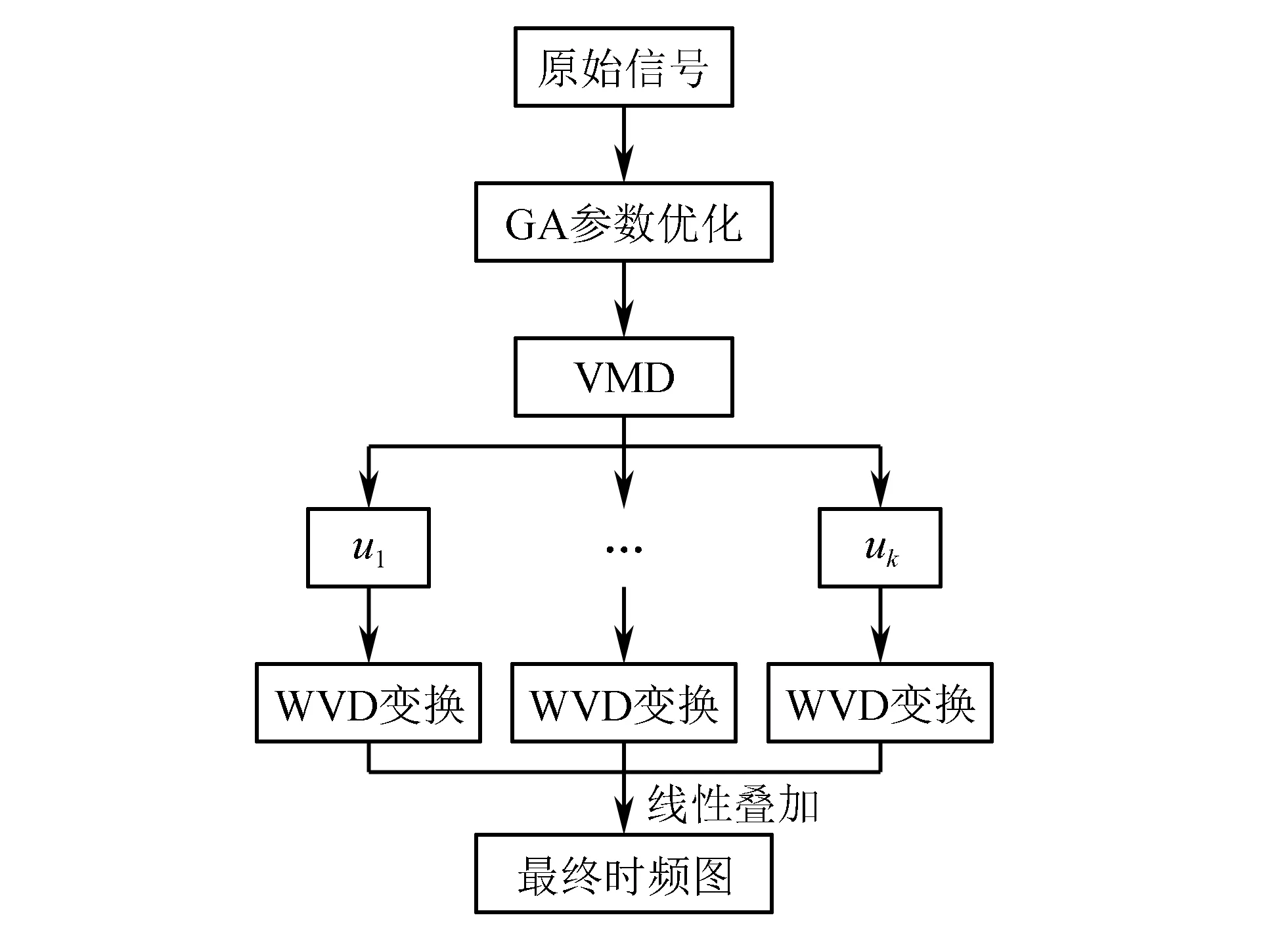
图2 遗传算法优化的VMD和WVD的时频分析方法流程
2 仿真验证
为了验证基于遗传算法参数优化的VMD-WVD算法的性能,进行仿真验证。信号为:
(8)
令
y(t)=y1(t)+y2(t)+y3(t)+y4(t),
(9)
直接通过WVD变换对式(9)进行时频分析,分析结果如图3所示。式(9)的信号共有4个信号分量,但由于交叉项的干扰,WVD变换的时频图信号分量大于4,时频图出现了失真现象。

图3 信号y(t)的WVD变换时频图
通过遗传算法优化参数的VMD-WVD方法对式(9)的信号进行时频分析,经遗传算法优化得到VMD分解的2个最优参数,k=4,α=439。图4为k=4,α=439信号的VMD分解的结果,图5为各模态函数的傅里叶变换频谱。

图4 k=4,α=43信号的VMD分解的结果

图5 各模态函数的傅里叶变换频谱
根据参数优化后的k值,原信号被分解为4个谐波形式的模态函数。图5分别对应图4的4个模态函数的傅里叶变换频谱。从图5可看出,VMD分解的4个分量分别与式(8)每个信号的频谱一一对应,无多余的分量。由于经VMD得到的信号是实信号,在进行时频分析前,需要对信号进行希伯尔特变换,再分别将得到的的结果进行WVD。

图6 信号的各模态函数的WVD变换时频谱
信号的各模态函数的WVD变换时频谱如图6所示。从图6可看出,经VMD方法分解得到的各模态函数含有一个信号分量,各个模态函数进行WVD变换后不再含有任何交叉项。将各个分量的WVD结果叠加,得到基于遗传算法优化参数的VMD-WVD变换的信号时频谱如图7所示。从图7可看出,除了属于信号本身的分量以外,不存在任何交叉项。仿真结果表明,对于一般信号来说,基于遗传算法优化参数的VMD-WVD方法具有良好的时频聚集性,且抑制了WVD的交叉项。
为了进一步验证基于遗传算法优化参数的VMD-WVD方法在微动特征提取中的作用,采用电磁仿真软件FEKO建立无人机的旋翼模型。雷达发射工作频率为5 Hz的单频信号,雷达与目标之间的俯仰角为45°,距离为5 m。考虑计算机的工作效率,仅将旋转速度设置为10 r/s,。旋翼叶片的长度为0.12 m,个数为2。仿真模型和仿真结果分别如图8、9所示。

图8 FEKO仿真模型
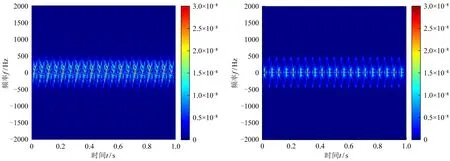
图9 FEKO仿真旋翼模型时频分析
从图9(a)可看出,闪烁点已经混在一起,周期和包络都不明显,且有很多的干扰项和WVD变换引起的交叉项存在,无法直接通过时频图得到相关的微动参数。图9(b)的时频图由基于遗传算法优化参数的VMD-WVD变换得到,通过遗传算法优化的VMD方法的参数分别为:模态个数k=5,惩罚因子α=2 000。从图9(b)可看出,共有20个闪烁点和包络,包络是与理论分析一致的正弦包络,且闪烁引起的亮点不再混叠在一起。从图9(b)可得到,T=(1/20)×2=0.1 s,转速fr=1/T=10,与仿真参数一致。实验结果表明,本方法不仅具有良好的时频分辨率,还克服了交叉项和干扰项对时频图的影响。
3 结束语
提出了一种基于遗传算法优化参数的VMD-WVD无人机微动特征的时频分析方法。该方法利用遗传算法自动寻找全局最优VMD参数,通过最优参数对无人机旋翼信号进行VMD分解得到若干个模态函数,并利用WVD对分解信号进行时频变换后进行线性叠加,得到原信号的时频分析结果。实验结果表明,该方法在保证良好时频聚集性情况下抑制交叉项干扰,使时频分析结果更为准确。

