矩阵方程AX=B及其最小二乘问题的一类广义对称解

彭振赟，尚邵阳，周昱洁

(桂林电子科技大学 数学与计算科学学院，广西 桂林 541004)

对称矩阵作为特殊的一类矩阵，不仅应用在数学的其他分支，在几何、物理、力学、工程技术中也有广泛的应用。将非对称矩阵“对称化”以解决与原矩阵相关的问题是诸多专家、学者考虑的问题。1936年，Kolmogorov用正定矩阵乘原矩阵，使其乘积成对称矩阵，从而解决了概率论中的一些问题。其实这些想法已于1922年就被Stenel采用[1]，他更一般地用非奇异实矩阵乘原矩阵，使之成为对称矩阵。这种矩阵乘积对称化的方法，自20世纪以来曾为不少学者解决某些问题的常用方法[2-3]。1988年，孙继广[4]讨论了实对称矩阵的两类逆特征值问题，给出了逆特征值问题的实对称解的表达式。2000年，孙家昶[5]为了研究求解二阶椭圆型非自共轭方程的离散迭代算法，定义了正定可对称化矩阵。2001年，张忠志等[6]研究了D反对称矩阵反问题，并利用矩阵奇异值分解、分块降阶的方法，得到了矩阵反问题的最小二乘解和最佳逼近解的一般表达式；2002年，易学军等[7]讨论了线性流型上D对称矩阵反问题。2002年，彭振赟等[8]利用矩阵的奇异值分解方法，讨论了非奇异乘积对称矩阵反问题，得到了此类矩阵反问题有解的充分必要条件及通解的表达式。2003年，彭振赟等[9-10]讨论了矩阵方程AX=B的子空间上对称解问题。2006年，龚丽莎等[11]讨论了矩阵方程AX=B的主子矩阵约束对称最小二乘解问题。

1 预备知识

定义给定矩阵M∈Rm×n，若矩阵X∈Rn×m满足XM∈SRn×n，则称X为M-对称矩阵。若矩阵X∈Rn×m满足XM∈ASRn×n。则称X为M-反对称矩阵。MSRn×n表示所有M-对称矩阵的集合，MASRn×n表示所有M-反对称矩阵的集合。用Rm×n表示全体实矩阵集合，SRn×n表示全体实对称矩阵集合，ASRn×n表示全体实反对称矩阵集合。A+表示矩阵A的Moore-Penrose广义逆，‖A‖F表示矩阵A的Frobenius范数，A*B表示矩阵A与B的Hadamard积，其定义为A*B=(AijBij)。

讨论如下几类问题：

问题Ⅰ给定M∈Rm×n，A∈Rp×n，B∈Rp×m,求X∈MSRn×n，使得

AX=B。

问题Ⅱ给定M∈Rm×n，A∈Rp×n，B∈Rp×m，X∈MSRn×n，使得

其中SEi(i=1,2)分别为问题Ⅰ和问题Ⅱ的解集合。

基于矩阵的奇异值分解，矩阵的广义奇异值分解，矩阵广义逆和矩阵分块方法，给出问题Ⅰ有解的充分必要条件和问题Ⅰ、Ⅱ的解的一般表达式，以及计算问题Ⅰ和问题Ⅱ的最佳逼近解的计算步骤和数值例子。

2 问题Ⅰ、Ⅱ和Ⅲ的解

引理1设矩阵M∈Rm×n的奇异值分解为

(1)

其中：U和V分别为m阶和n阶正交矩阵；Σ=diag(δ1,δ2,…，δr)>0；r=rank(M)，则X∈MSRn×n可表示为

(2)

其中：X11∈Rr×r满足X11Σ∈Rr×r；X12∈Rr×(m-r)；X22∈R(n-r)×(n-r)。

证明由矩阵M的奇异值分解，有

令

(3)

其中：X11∈Rr×r；X12∈Rr×(m-r)；X22∈R(n-r)×(n-r)，则

注意到XM∈SRn×n，则有

X11Σ∈SRr×r，X21Σ=0。

因为Σ非奇异，则有X21=0。因此，矩阵X∈MSRn×n可以表示为式(2)。

引理2[12]矩阵方程AX=B有解X∈Rn×m的充分必要条件是AA+B=B，且有解时其解的一般表达式可表示为

X=A+B+(I-A+A)G,

其中G为适当阶数的任意矩阵。

X=A+B+(I-A+A)G，

其中G为适当阶数的任意矩阵。

引理4[12-13]矩阵方程AX=B有解X∈SRn×n的充分必要条件

AA+B=B，ABT=BAT，

且有解时其解的一般表达式可表示为

X=A+B+(I-A+A)(A+B)T+

(I-A+A)G(I-A+A)，

其中G为适当阶数的任意对称矩阵。进一步，若矩阵A∈Rm×n的奇异值分解为

其中：U=(U1,U2)和V=(V1,V2)分别为m阶和n阶正交矩阵；U1∈Rm×r,V1∈Rn×r；Σ=diag(δ1,δ2,…,δr)>0；r=rank(A)，则矩阵方程AX=B在X∈SRn×n内有解时,其解可表示为

X=A+B+(I-A+A)(A+B)T+V2GV2，

其中G为适当阶数的任意对称矩阵。

引理5[4]设G∈Rr×r，Σ=diag(σ1,σ2,…,σr)>0，则问题

‖SΣ-G‖F=min，

在S∈SRn×n内存在唯一解

其中

引理6设D为非奇异对称矩阵，则XD是对称矩阵的充分必要条件是D-1X为对称矩阵。

证明注意到D为非奇异对称矩阵，则有

(XD)T=XD⟺DXT=XD⟺XTD-1=

D-1X⟺(D-1X)T=D-1X,

故命题成立。

引理7[14]设D1=diag(α1,α2,…,αn)>0，D2=diag(β1,β2,…,βn)>0，则问题min‖D1GD2-E‖在SRn×n中存在唯一解

G=Φ*(D1ED2+D2ETD1)。

定理1设矩阵M的奇异值分解为式(1)，令

AV=(A1,A2)，BU=(B1,B2)，

(4)

其中：A1∈Rp×r，B1∈Rp×r，则问题Ⅰ有解的充分必要条件为

(5)

进一步，若矩阵A1的奇异值分解为

(6)

X=V(Y,Z)UT，

(7)

其中：

(8)

Z=(AV)+B2+[I-(AV)+AV]G2；

(9)

G1为适当阶数的任意对称矩阵；G2为适当阶数的任意矩阵。

证明由AX=B和式(2)，有

因而有

A1X11=B1，X11Σ∈SRr×r

(10)

和

(11)

根据引理4可知，式(10)有解的充要条件为

且有解时其解可表示为

其中G1为适当阶数的任意对称矩阵。由引理2可知式(11)有解的充分必要条件为

AV(AV)+B2=B2，

且有解时其解可表示为

其中G2为适当阶数的任意矩阵。记

则问题Ⅰ的解可表示为式(7)。

定理2设矩阵M的奇异值分解为式(1)，并按式(4)将矩阵AV和BU进行分块，则A1Σ奇异值分解为

(12)

其中：Λ=diag(λ1,λ2,…,λs)>0；s=rank(A1Σ)；P=(P1,P2)和Q=(Q1,Q2)分别为p阶和r阶正交矩阵；P1∈Rp×s，Q1∈Rr×s。令

(13)

其中B11∈Rs×s，B22∈R(r-s)×(r-s)，则问题Ⅱ的解可表示为

X=V(Y,Z)UT，

(14)

Z=(AV)+B2+(I-(AV)+AV)G2，

其中

(15)

G1为适当阶数的任意对称矩阵，G2∈Rn×(m-r)为任意矩阵。

证明由Frobenius范数的正交不变性，有

因此，问题II等价于

由引理3可知

(16)

G2∈Rn×(m-r)为任意矩阵。由引理6有

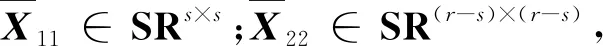
等价于

因此，X11可表示为

(17)

其中G1为适当阶数的任意对称矩阵。由式(2)、(16)和(17)可知，问题Ⅱ的解可表示为式(14)。

(18)

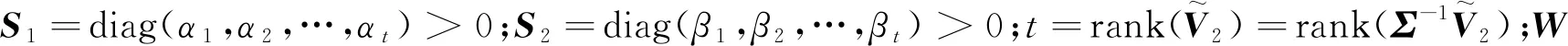
(19)

(20)

若SE1非空，则问题Ⅲ在SE1中的解为

(21)

其中

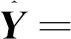
(22)

(23)

(24)

{I-[I-(AV)+AV]+[I-(AV)+AV]}G3，

(25)

G3为适当阶数的任意对称矩阵。

证明由定理1及Frobenius范数的正交不变性，有

则最佳逼近问题

等价于

由引理2和引理7可知问题Ⅲ在SE1中的解可表示为式(21)。

(26)

其中：

Λ1=diag(γ1,γ2,…,γt)>0；

Λ2=diag(μ1,μ2,…,μt)>0；

t=rank(Q2)=rank(ΣQ2)；

(27)

若SE2非空，则问题Ⅲ在SE2中的解为

(28)

其中

(29)

(30)

(31)

{I-[I-(AV)+AV]+[I-(AV)+AV]}G3，

(32)

G3为适当阶数的任意对称矩阵。

证明由定理2及Frobenius范数的正交不变性，有

则最佳逼近问题

等价于

由引理2和引理7可知，问题Ⅲ在SE2中的解可表示为式(28)。

3 算法与数值例子

考虑到各问题的计算方法具有相似性，只给出计算问题Ⅲ在SE1中的一个解的算法步骤，即算法1。

算法1计算问题Ⅲ在SE1中的一个解的算法步骤：

2)按式(1)做矩阵M的奇异值分解；

3)按式(4)将矩阵AV和BU进行分块；

4)若式(5)成立，则SE1非空。因而问题Ⅲ在SE1中有解；否则，问题Ⅲ在SE1中无解；

5)按式(6)做矩阵A1的奇异值分解；

8)按式(20)计算矩阵E；

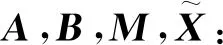
且

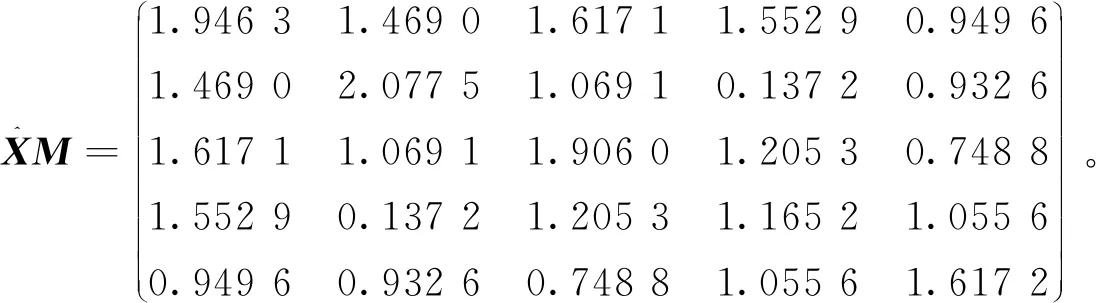
4 结束语

针对矩阵方程AX=B及其最小二乘问题，讨论了一类广义对称解。基于矩阵的奇异值分解，矩阵的广义奇异值分解，矩阵广义逆和矩阵分块方法，给出问题Ⅰ有解的充分必要条件和问题Ⅰ、Ⅱ的解的一般表达式，以及计算问题Ⅰ和问题Ⅱ的最佳逼近解的计算步骤和数值例子。